УДК 621.371+537.87

БЛИЖНЕПОЛЬНАЯ ИМПУЛЬСНАЯ СВЧ ДИАГНОСТИКА ПОДПОВЕРХНОСТНЫХ ДИЭЛЕКТРИЧЕСКИХ НЕОДНОРОДНОСТЕЙ

К. П. Гайкович^1,2, Е. С. Максимович³

 ¹ Институт физики микроструктур Российской академии наук, г. Нижний Новгород

² Нижегородский государственный университет им. Н.И. Лобачевского

 ³ Институт прикладной физики Национальной академии наук Беларуси, г. Минск

Статья поступила в редакцию 30 января 2016 г. 

 

Аннотация. Приводятся первые результаты исследования метода импульсной СВЧ диагностики трехмерных распределений комплексной диэлектрической проницаемости подповерхностных диэлектрических неоднородностей. Диагностика основана на решении обратной задачи ближнепольного рассеяния по данным двумерного сканирования приемо-передающей системой. В статье предлагается алгоритм решения обратной задачи рассеяния, и демонстрируются результаты томографии и голографии тестовых подповерхностных объектов в ближней зоне зондирующего сигнала.

Ключевые слова: томография, голография, диэлектрик, неоднородные среды, рассеяние СВЧ излучения.

Abstract. First investigation results are given for a new method of pulse diagnostics of 3D distributions of complex permittivity of subsurface dielectric inhomogeneities. This diagnostics is based on the solution of the near-field inverse scattering problem by data of 2D scanning with the transceiver system. In this paper a solving algorithm is proposed for this inverse scattering problem, and results of tomography and holography of test subsurface targets in the near field zone of the probing signal are demonstrated.

Key words: tomography, holography, dielectric, inhomogeneous media, scattering of microwave radiation.

 

 1.                 Введение

Ближнепольная СВЧ диагностика основана на решении обратной задачи рассеяния по данным СВЧ измерений поля, рассеянного диэлектрическими объектами на глубине порядка размеров ближней зоны в среде для наибольшей длины волны частотного диапазона зондирующего сигнала. Диагностика объемных неоднородностей включает компьютерную томографию (получение трехмерного (3D) распределения) комплексной диэлектрической проницаемости распределенных подповерхностных неоднородностей и голографию (определения формы поверхности) сплошных диэлектрических объектов.

Ближнепольные измерения привлекают возможностью выхода за релеевское ограничение разрешающей способности, что является единственным способом в случае, когда переход к более коротковолновому диапазону невозможен из-за сильного ослабления поля в среде. Эта возможность может быть особенно востребованной в медико-биологических приложениях. В работах [1-4] были развиты различные подходы к такой диагностике, основанные на измерениях рассеянного сигнала в двумерной области над областью среды с подповерхностными неоднородностями при ее зондировании непрерывным гармоническим сигналом. До некоторой степени аналогичные подходы в настоящее время развиваются и с целью получения двумерных радиоголографических изображений подповерхностных металлических неоднородностей [5].

Для диагностики трехмерных неоднородностей недостаточно данных двумерного сканирования, поэтому глубинную чувствительность обеспечивают измерения в зависимости от третьего параметра. В [1-4] были предложены методы, в которых в качестве такого параметра использовались частота сигнала, размер апертуры приемной антенны или расстояние от уровня сканирования до поверхности среды.

В данной работе развивается новый подход к ближнепольной сканирующей томографии, основанный на использовании импульсного зондирующего сигнала, где глубинную чувствительность определяет временная зависимость рассеянного импульса. В нем используется схема измерений, предложенная в [2], в которой измерения в двумерной области над неоднородностью выполняются с помощью жестко связанной системы “источник-приемник”. Такая схема, использованная в [2-4], приводила 3D уравнение для рассеянного сигнала в борновском приближении к уравнению типа свертки, редуцируемому к одномерному интегральному уравнению, которое решалось для каждой пары волновых чисел двумерного поперечного спектра.

Это позволило преодолеть принципиальные ограничения численного решения на размерность, возникающие в трехмерных задачах. Было также показано, что этот подход позволяет получать и некоторую коррекцию к решению в борновском приближении. Поперечные спектры функций Грина, образующие ядро решаемых уравнений, были получены в [2] в явном виде. Там же был апробирован и метод решения таких уравнений Фредгольма 1-го рода для комплекснозначных функций в пространстве Соболева основанный на принципе обобщенной невязки. Описанный метод томографии был реализован в эксперименте для метода многочастотной подповерхностной СВЧ томографии неоднородностей в грунте [3,4], где оказалось возможным получить томографические и голографические изображения субволнового разрешения диэлектрических объектов в слабо поглощающих средах до глубин около 10 см.

В данной статье представлены постановка обратной задачи рассеяния для ближнепольной импульсной СВЧ диагностики, соответствующая математическая теория, алгоритмы методов томографии и голографии, а также первые результаты экспериментов по зондированию подповерхностных неоднородностей в импульсном режиме. Среди возможных применений этой методики весьма важными представляются ее использование в дефектоскопии и медико-биологических приложениях.

2.                 Теория

Предлагаемая ближнепольная диагностика основана на решении обратной задачи рассеяния по данным измерений двумерного распределения связанных с неоднородностью вариаций комплексных амплитуд принимаемого сигналапо поперечным координатам x_r и y_r, измеряемого при сканировании на уровне z_r (r_r – вектор, определяющий положение приемника).

 

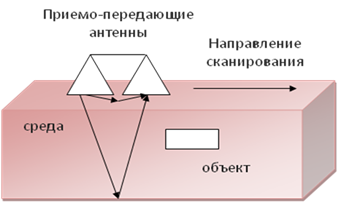
Рис.1. Схема измерений.

 

Эти вариации связаны с вариациями рассеянного поля, распределение которого в среде с неоднородностями можно определить с использованием формализма функций Грина, которые, однако, неизвестны для полей с произвольной временной зависимостью. Но, поскольку они известны для полей, порождаемых гармоническим сигналом в произвольных многослойных средах [2], естественным представляется использовать в анализе разложение импульсного сигнала, заданного в интервале , в частотный спектр:

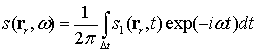                                 ,                                 (1)

 

который имеет вид свертки по поперечным координатам рассеянного поля с передаточной функцией измерительной системы:

                                        (2)

Выполняя двумерное преобразование Фурье по поперечным координатам x_r и y_r, получаем интегральное соотношение для поперечного спектра трансформированного сигнала:

                                                            (3)

Если в среде с комплексной диэлектрической проницаемостью имеется рассеивающая трехмерная неоднородность , так что , то комплексные амплитуды электрического поля на частоте  могут быть представлены как сумма зондирующего и рассеянного полей. Для предлагаемой схемы сканирования (см. на рис.1) жестко связанной системой источник-приемник, взаимное положение которых определяется вектором , определяющим сдвиг между приемной и передающей антеннами, поперечный спектр рассеянного поля (двумерное фурье-преобразование по x и y) в борновском приближении может быть представлен как интеграл от глубинного профиля поперечного спектра неоднородностей в виде [2]:

 

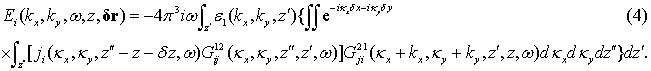
Подставляя (4) в формулу (3), имеем интегральное уравнение:

                                                     (5)

   

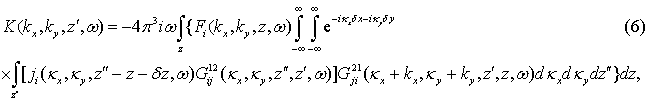
ядро которого K  выражается через компоненты поперечного спектра тока j и функций Грина для волн, распространяющихся из среды 1 в среду 2 и обратно [2]. Интегральное уравнение (6) формально совпадает с уравнением, которое лежит в основе метода многочастотного ближнепольного зондирования [2-4], однако в данном случае исходные данные для решения обратной задачи (5) получаются путем разложения импульсного сигнала в частотный спектр. При численном решении такой задачи параметрами становятся шаг разложения по частоте и ширина спектрального интервала анализа. Учитывая, что сигнал является действительной величиной, в решении (5) может использоваться только положительная часть спектра сигнала.

Для решения (5) может применяться алгоритм метода обобщенной невязки для комплекснозначных функций, развитый в [2]. В результате из решения в k-пространстве задачи (5) путем обратного фурье-преобразования получается решение задачи томографии – искомая трехмерная структура комплексной диэлектрической проницаемости:

                                            (7)

Используя аналогию математического аппарата, так же, как в методе многочастотного СВЧ зондирования [3,4], можно предложить метод компьютерной голографии (восстановления формы поверхности) сплошных, внутренне однородных объектов, которые чаще всего встречаются на практике. Если a priori известно, что диэлектрическая проницаемость объекта постоянна, то задача томографии может быть редуцирована к задаче восстановления числовой формы объекта, используя полученное из (5) решение задачи томографии в k-пространстве, в виде двух функций из решения комплексного трансцендентного уравнения, которое эквивалентно системе двух реальных уравнений:

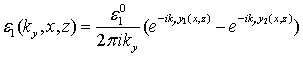                    ,                                     (8)

                             

 

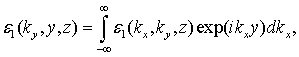
что и позволяет получить из его решения обе функции, определяющие форму объекта. Переопределенность этого уравнения позволяет различным образом оптимизировать алгоритмы его решения.

3.                 Результаты эксперимента

В экспериментах использовалась та же сканирующая система, что и в экспериментах [3,4] для многочастотной подповерхностной СВЧ диагностики. В импульсном зондировании аппаратура включала в себя цифровой осциллоскоп GZ10E, генераторную головку с центральной рабочей частотой 3,5 ГГц спектра сигнала в форме моносинуса, а также приемо-передающие широкополосные bow-tie дипольные антенны, имеющие широкий пространственный спектр передаточной функции. Сканирование осуществлялось по сетке 3951 точек с шагом 0,5 cм. Измерения выполнялись для объекта из пенопласта размерами 331 см³  на глубинах z_t = –0,5,–1,–2,…, –10 см в песчаной среде с диэлектрической проницаемостью +0,05i.

 

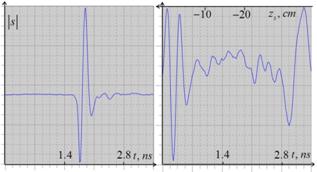
Рис.2.  а) зондирующий импульс; b) рассеянный сигнал при глубине объекта z_t = –2 см.

На рис.2 представлены результаты измерений рассеянного сигнала, в котором вместо параметра временной зависимости t используется зависимость от параметра эффективной глубины рассеивающего элемента z_s согласно. Нулевое значение параметра z_s соответствует времени прихода сигнала, рассеянного от поверхности среды. Зондирующий импульс генератора и импульс рассеянного сигнала от заглубленного на 2 см объекта показаны как во временном масштабе, так и в соответствующем масштабе эффективной глубины рассеивающего элемента. Помимо отклика от зондируемого объекта виден также отклик от дна емкости (при z_s ~ –30 см). На рис.3 представлены результаты измерений распределения амплитуды рассеянного импульса вдоль линии, проходящей над центром объекта при его положении на различных уровнях по глубине, в зависимости от параметра эффективной глубины рассеяния.

 

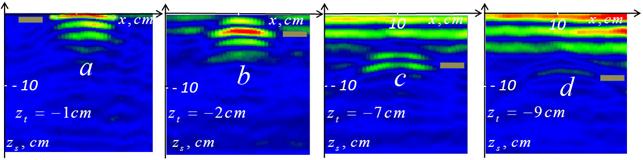
Рис.3. Амплитуда рассеянного импульса  вдоль направления оси x при

y = 10 см (над центром заглубленного объекта) в зависимости от эффективной глубины рассеивающего элемента z_s
 для объекта на различных глубинах z_t: а) z_t = –1 см; b) z_t = –2 см; c) z_t = –7 см; d) z_t = –9 см.
Вставки показывают глубинное положение зондируемого объекта на оси z_s.

 

На рисунках отчетливо видны области отклика, соответствующие глубине залегания объекта. Длинные полосы на рисунках соответствуют отражению от слоистой структуры плотности среды, возникающей при заглублении объекта путем последовательного досыпания грунта. В этой связи интересно отметить, что проявление в сигнале таких вариаций указывает на возможность постановки задачи восстановления глубинного профиля одномерных неоднородностей такого типа. На рис.4 показаны распределения амплитуды рассеянного импульса в поперечном сечении для нескольких значений параметра эффективной глубины рассеяния вокруг истинной глубины залегания объекта. Видно, что при значениях z_s, соответствующих глубинам объектов (z_t = –2 см, z_t = –7 см), эти объекты различимы наиболее отчетливо. Более того, в них до некоторой степени проявляются особенности формы объекта. Такая визуализация исходных данных весьма полезна для предварительной локализации положения объекта с целью сужения области поиска решения, что может существенно уточнить результаты последующего предложенного выше анализа.

 

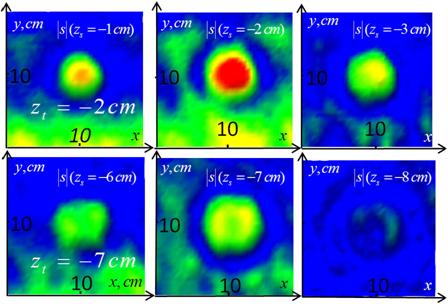
Рис.4. Амплитуда рассеянного импульса  для объектов на двух различных глубинах:
Верхний ряд: объект на глубине z_t = –2 см; распределения показаны в трех сечениях по величине
параметра эффективной глубины рассеяния:,, .
Нижний ряд: объект на глубине z_t = –7 см; показаны распределения при,,

 

На рис.5 показаны частотные спектры рассеянного сигнала в k-пространстве, которые являются входными данными для решения обратной задачи томографии на основе интегрального уравнения (5) для объектов на глубинах z_t = –1, –2 –7, –9 см вдоль линии, проходящей через центр неоднородностей.

 

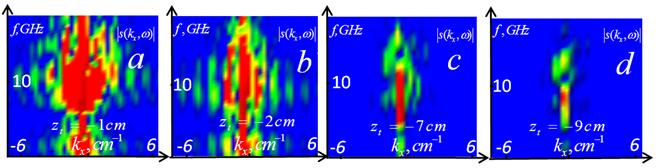
Рис.5. Амплитуда частотного распределения поперечного спектра рассеянного импульса
 для объектов на глубинах: a) z_t = –1 см; b) z_t = –2 см; c) z_t = –7 см; d) z_t = –9 см.

 

Можно видеть, что с ростом глубины залегания объекта за пределы ближней зоны сужается пространственный спектр рассеянного сигнала, то есть в нем хуже представлены мелкомасштабные детали объекта. Таким образом, приведенные результаты исследования сигнала показывают, что импульсные измерения являются информативными, а это создает необходимые условия для успешного применения предложенных методов ближнепольной диагностики.

На рис.6 представлены результаты решения задачи томографии – восстановление распределения реальной части комплексной диэлектрической проницаемости из решения уравнения (5).

 

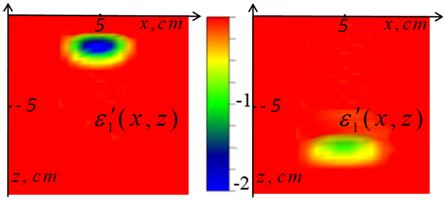
Рис.6. Результаты томографического анализа – томографические разрезы восстановленного распределения
в вертикальной плоскости через центр объекта по оси y.
Слева – для объекта на глубине z_t = –2 см; справа – на глубине z_t = –7 см.

 

Изображения демонстрируют хорошее согласование с реальными размерами, положением и общей формой объектов. Также, для объекта на глубине z_t = –2 см имеет место хорошее согласование по величине ; однако с увеличением глубины изображение объекта расплывается, и погрешность решения постепенно возрастает – что является следствием затухания мелкомасштабных ближнепольных компонент сигнала, которое можно видеть из сравнения рис.5b и рис.5c.

На рис.7. показаны результаты голографического анализа для тех же объектов, что и на рис.6.

 

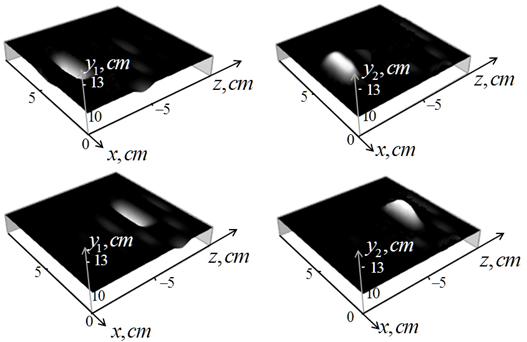
Рис.7. Результаты голографического анализа. Верхний ряд – на глубине zt = –2 см; нижний ряд – на глубине zt = –7 см. В рядах слева – голографические изображения половины зондируемых объектов, представленные функцией y1(x,z); справа – половины, представленные функцией y2(x,z).

 

Изображения на рис.7 хорошо воспроизводят форму объекта на  глубине z_t = –2 см и демонстрируют ее расплывание при z_t = –7 см (при удалении за пределы ближней зоны для высокочастотных компонент спектра сигнала). Следует подчеркнуть, что это только первые результаты, которые, несомненно, могут быть улучшены при оптимизации параметров измерения и алгоритмов обработки данных. В целом, результаты работы показывают перспективность предложенного метода для подповерхностной диагностики, как для указанных во введении приложений СВЧ зондирования, так и в других диапазонах электромагнитных волн, или в акустическом зондировании.

 

Исследования были выполнены при поддержке РФФИ, проекты № 15-47-02294-р_поволжье, 16-52-00051-Бел, отдельного проекта научных исследований НАН Беларуси № гос. регистрации 20140818, программы ОФН РАН IV.13, а также частично поддержаны грантом Минобрнауки РФ (соглашение от 27 августа 2013 г. № 02.В.49.21.0003 между МОН РФ и ННГУ).

 

Литература

1.     Gaikovich K.P. Subsurface Near-Field Scanning Tomography // Physical Review Letters, vol. 98, no. 18, pp. 183902 (1-4), 2007.

2.     Gaikovich K.P., Gaikovich P.K. Inverse problem of near-field scattering in multilayer media // Inverse Problems, vol. 26, no. 12, pp. 125013 (1-17 pp.), 2010.

3.     Gaikovich K.P., Gaikovich P.K., Maksimovitch Ye.S., Badeev V.A. Pseudopulse near-field subsurface tomography // Physical Review Letters, vol. 108, no. 16, pp. 163902 (1-5 pp.) , 2012.

4.     Gaikovich K.P., Gaikovich P.K., Maksimovitch Ye.S., Badeev V.A. Subsurface near-field microwave holography // IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing., vol. PP, issue 99, pp.1-9 (IEEE Early Access Articles), 2015.

5.     Razevig V.V., Ivashov S.I., Sheyko A.P., Vasiliev I.A., Zhuravlev A.V. An example of holographic radar using at restoration works of historical building // Progress in Electromagnetic Research Letters., vol.1, pp. 173-179, 2008.