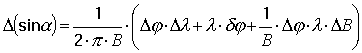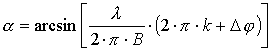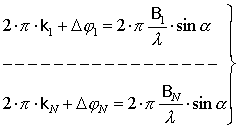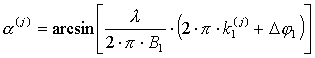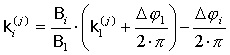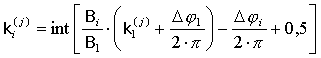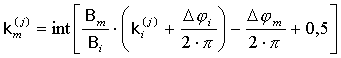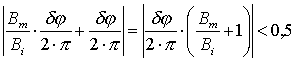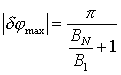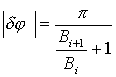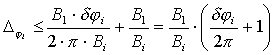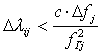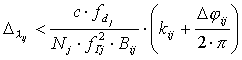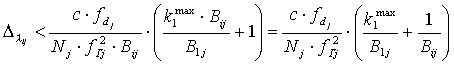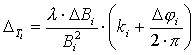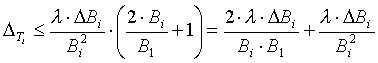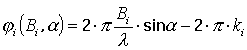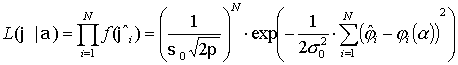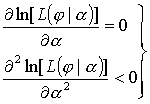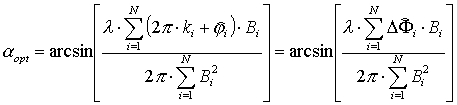|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 1, 2002 |
|
АЛГОРИТМ ОПРЕДЕЛЕНИЯ УГЛА ПРИХОДА СИГНАЛА С ПОМОЩЬЮ НЕЭКВИДИСТАНТНОЙ АНТЕННОЙ РЕШЕТКИ
Гайдученко А.Б.
Московский Государственный инженерно-физический
институт (технический университет)
Получена 25января 2002
В данной работе рассматриваются некоторые теоретические подходы к определению направления прихода радиосигнала с помощью линейных неэквидистантных антенных решеток (АР). Предложен алгоритм определения направления прихода сигнала с помощью неэквидистантной линейной АР с расстояниями между элементами (базами), большими длины полуволны сигнала. Большинство известных методов определения пеленга сигнала базируется на условии, заключающемся в том, что хотя бы одна из баз АР должна иметь линейный размер, не превышающий половины длины волны принимаемого сигнала.
1. Алгоритм
определения направления прихода сигнала
3. Оценка угла прихода сигнала методом максимального правдоподобия
1. Алгоритм определения направления прихода сигнала
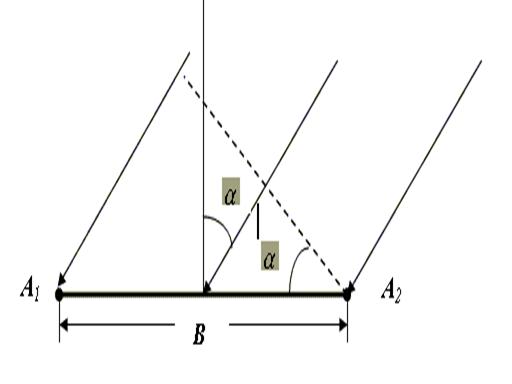
Весьма точным и быстродействующим является фазовый метод, заключающийся в измерении разности фаз между сигналами, принятыми соседними элементами антенной решетки [1]. Из рис. 1 видно, что полная разность фаз между сигналами с соседних элементов АР равна:
Рисунок 1. Двухэлементная антенная решетка.
Разность фаз, которую можно непосредственно
измерить (например, с помощью преобразований Гильберта или Фурье
[2,3]),
лежит в диапазоне от
![]() до
до
![]() .
Как следует из (1),
для того, чтобы разность фаз лежала в этих пределах, необходимо соблюдение
условия:
.
Как следует из (1),
для того, чтобы разность фаз лежала в этих пределах, необходимо соблюдение
условия:
![]()
Только в этом случае направление прихода сигнала может быть определено однозначно. Однако очевидным недостатком данного метода является его высокая чувствительность к погрешностям измерения длины волны и разности фаз. Действительно:
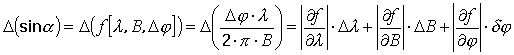
Точность определения угла можно повысить
путем увеличения длины базы АР. Однако, в случае двухэлементной АР с базой,
превышающей половину длины волны, разность фаз между сигналами с соседних
элементов может превысить по величине
![]() ,
и определение угла становится неоднозначным.
,
и определение угла становится неоднозначным.
Цифровые методы обработки сигналов (например, использование ДПФ) позволяют
измерить разность фаз лишь в пределах от
![]() до
до
![]() .
Несмотря на то, что областью значений арктангенса без учета периодичности
является интервал
.
Несмотря на то, что областью значений арктангенса без учета периодичности
является интервал
![]() ,
это можно сделать, зная знаки и величины действительной и мнимой частей в
спектре сигнала
[3]. При этом величина разности фаз между сигналами с двух соседних
элементов трактуется следующим образом:
,
это можно сделать, зная знаки и величины действительной и мнимой частей в
спектре сигнала
[3]. При этом величина разности фаз между сигналами с двух соседних
элементов трактуется следующим образом:
![]() , если
, если
![]() ;
;
![]() , если
, если
![]() ;
(3)
;
(3)
![]() ,
если
,
если
![]() ;
;
Таким образом, в общем случае полная фаза
![]() равна
сумме частичной фазы
равна
сумме частичной фазы
![]() (которую
можно получить путем непосредственного измерения) и величины
(которую
можно получить путем непосредственного измерения) и величины
![]() (где
целое
k выражает неопределенность измерения
фазы):
(где
целое
k выражает неопределенность измерения
фазы):
Отсюда, при условии, что неопределенность фазы устранена (найдена величина k), можно найти искомый угол:
Трудность состоит в том, что при наличии единственной базы нельзя определить однозначно величину неопределенности фазы k. Например, в случае базы длиной в полторы длины волны k может принимать значения -1; 0; 1.
Таким образом, возникает задача разработки
алгоритмов, позволяющих устранить неопределенность в расчетах угла прихода
сигнала, обеспечивающих устойчивость решений в условиях присутствия
амплитудных и фазовых шумов с учетом требований к превышению минимальными
базами величины
![]() .
.
Рассмотрим АР, состоящую из нескольких баз
Bi
(i = 1, …,
N). С учетом (5)
для каждой базы
Bi
имеем
уравнение, связывающее коэффициент неопределенности фазы
k с углом прихода сигнала
![]() ,
длиной волны сигнала
,
длиной волны сигнала
![]() ,
величиной базы
Bi
и измеряемой разностью фаз
,
величиной базы
Bi
и измеряемой разностью фаз
![]() :
:
Система состоит из
N уравнений с (N + 1) неизвестными: коэффициенты неопределенности фазы
k
i (i = 1,….,
N) и угол прихода сигнала
![]() ;
длина волны
;
длина волны
![]() также
является измеряемой величиной и определяется путем оценки частоты несущей
сигнала. Геометрия антенной решетки, т.е. известные межэлементные расстояния,
может дать дополнительные ограничения. Выберем для определенности, что размер
первой базы
также
является измеряемой величиной и определяется путем оценки частоты несущей
сигнала. Геометрия антенной решетки, т.е. известные межэлементные расстояния,
может дать дополнительные ограничения. Выберем для определенности, что размер
первой базы
![]() .
При этих условиях коэффициент
k1, в зависимости от
.
При этих условиях коэффициент
k1, в зависимости от
![]() ,
может принимать лишь одно из следующих значений: k1 = -1; 0; 1. При
этом верным будет лишь одно из этих значений. Дополнительным фактором,
помогающим решить систему (6)
является то, что все коэффициенты
ki
– целые числа. Следует также заметить, что при сокращении угла
обзора количество коэффициентов k1 может лишь уменьшиться.
,
может принимать лишь одно из следующих значений: k1 = -1; 0; 1. При
этом верным будет лишь одно из этих значений. Дополнительным фактором,
помогающим решить систему (6)
является то, что все коэффициенты
ki
– целые числа. Следует также заметить, что при сокращении угла
обзора количество коэффициентов k1 может лишь уменьшиться.
В зависимости от значения k1
и известной разности фаз сигналов![]() на первой базе можно найти набор возможных углов:
на первой базе можно найти набор возможных углов:
Здесь индекс j указывает на номер коэффициента k1 из набора возможных значений. Из всех значений угла правильным будет только одно. Более того, величина в квадратных скобках может превысить по модулю 1, что свидетельствует о том, что выбранное значение k1 не соответствует действительности.
В случае линейной АР угол прихода сигнала на любую из баз одинаков. Тогда, взяв отношение первого и i-го уравнений из (6), получим
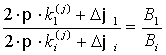
Откуда получаем выражение взаимосвязи размеров баз и коэффициентов неопределенности фазы. Например, связь остальных баз с первой определяется выражением:
Взяв целую часть, получим:
Это позволяет определить набор коэффициентов ki для любой i – ой базы по известному набору коэффициентов k1 для первой базы. Точно таким же образом возможно определение коэффициента km на m – ой базе по коэффициенту ki на предыдущей i – ой базе (i < m):
Такая гибкость вычислений позволяет повысить живучесть системы, т.е. обеспечить работоспособность при отказе одной, в частности первой, базы, но это потребует незначительного повышения вычислительных затрат.
Итак, каждый коэффициент
![]() порождает
целую последовательность коэффициентов
порождает
целую последовательность коэффициентов
![]() для
баз
Bi
(i = 2,….,
N). Но только для одной такой порожденной
последовательности (номер ее зависит от действительного угла прихода сигнала)
значения углов, вычисленных для каждой базы в соответствии с (7),
будут совпадать. Причем совпадение будет либо точным (при отсутствии ошибок
измерения фазы), либо последовательность вычисленных углов будет иметь
наименьший разброс значений (при наличии ошибок измерения фазы). Критерием
выбора угла из набора значений может быть условие:
для
баз
Bi
(i = 2,….,
N). Но только для одной такой порожденной
последовательности (номер ее зависит от действительного угла прихода сигнала)
значения углов, вычисленных для каждой базы в соответствии с (7),
будут совпадать. Причем совпадение будет либо точным (при отсутствии ошибок
измерения фазы), либо последовательность вычисленных углов будет иметь
наименьший разброс значений (при наличии ошибок измерения фазы). Критерием
выбора угла из набора значений может быть условие:
![]()
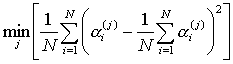 ,
,
где i = 1,…, N – номер базы АР, j = 1,…, M – номер порождающей последовательности.
Рассмотрим общий случай для последовательности баз, когда коэффициент неопределенности фазы для каждой последующей базы определяется по предыдущей базе, как в (10). Примем для простоты, что размеры баз расположены в порядке возрастания: B1 < B2 < …< BN-1 < BN . Пусть набор k1 для первой базы задан. Тогда
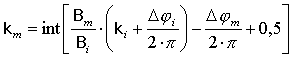
Введя погрешность определения частичной фазы
![]() ,
можно записать:
,
можно записать:
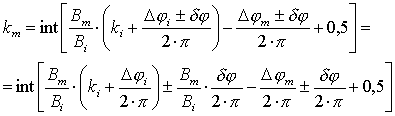
Таким образом, условие для максимально
допустимой погрешности определения частичной фазы
![]() ,
которая не приводит к возникновению погрешностей в определении
km
,
которая не приводит к возникновению погрешностей в определении
km
![]() , можно записать следующим
образом:
, можно записать следующим
образом:
Это условие определяет погрешность вычисления km , не превышающую единицу (для больших баз, где km велико, это составляет единицы процентов). В случае если длины баз растут от первой к последней, отношение длин последней и первой баз будет максимальным. Тогда условие для предельно допустимой погрешности измерения фазы в случае расчета коэффициентов только по первой базе:
Однако отношение длин соседних баз может быть гораздо меньше, а поэтому при расчетах ki по предыдущей базе (а не по первой) можно допустить, чтобы погрешность измерения фазы была больше, без ущерба для точности расчета:
Рассмотрим остальные погрешности определения
угла в зависимости от различных факторов. Обозначим погрешность определения
разности фаз на каждой базе
![]() .
Погрешность от всех параметров в (5):
.
Погрешность от всех параметров в (5):
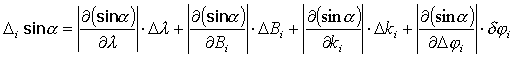
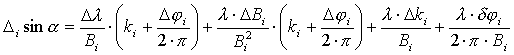
![]() ,
(13)
,
(13)
где
![]() -
соответственно методические погрешности (включая погрешности измерения и
округления) и технологические погрешности (точность монтажа решетки).
-
соответственно методические погрешности (включая погрешности измерения и
округления) и технологические погрешности (точность монтажа решетки).
Методическая погрешность есть сумма погрешностей, вызываемых ошибками определения длины волны и определения фазы:
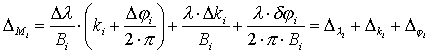
Влияние погрешности определения фазы на каждой базе (учитывая и то, что она влияет и на расчет коэффициента ki):
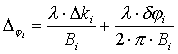
Учитывая, что
![]() ,
получим:
,
получим:
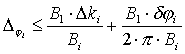
Если система работает в штатном режиме (т.е.
выполняется условие (11)),
то коэффициент
ki
определяется с максимальной погрешностью
![]() ,
значит
,
значит
Рассмотрим погрешность определения угла в зависимости от погрешности длины волны для заданного диапазона Dj и заданной базы Bi:
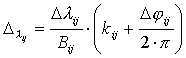
Величина
![]() определяется
исходя из разрешающей способности дискретного преобразования Фурье
определяется
исходя из разрешающей способности дискретного преобразования Фурье
![]() ,
причем
,
причем
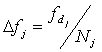 ,
где
,
где
![]() -
частота дискретизации,
Nj
– объем выборки в
j
– ом диапазоне. При постоянном шаге по частоте (
-
частота дискретизации,
Nj
– объем выборки в
j
– ом диапазоне. При постоянном шаге по частоте (![]() =
const)
шаг по длине волны
=
const)
шаг по длине волны
![]() будет
непостоянным, а будет зависеть от номера
n частотного отсчета ДПФ, т.е.
будет
непостоянным, а будет зависеть от номера
n частотного отсчета ДПФ, т.е.
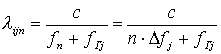 ,
n = 0,1,…,
N-1,
(15)
,
n = 0,1,…,
N-1,
(15)
где
![]() -
частота гетеродина в
j
– ом диапазоне, с – скорость света.
-
частота гетеродина в
j
– ом диапазоне, с – скорость света.
Тогда из (15) имеем:
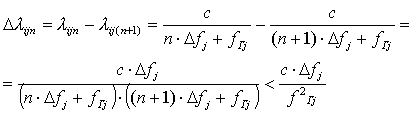
Таким образом, погрешность определения длины волны в заданном диапазоне независимо от номера отсчета удовлетворяет неравенству:
Поскольку
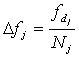 ,
то
,
то
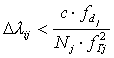 .
Отсюда, с учетом (16),
зависимость ошибки определения угла от ошибки определения длины волны имеет
вид:
.
Отсюда, с учетом (16),
зависимость ошибки определения угла от ошибки определения длины волны имеет
вид:
Как следует из (10)
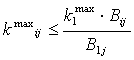 ,
а
,
а
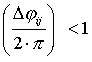 ,
тогда
,
тогда
Можно считать, что
![]() ,
т.к. ширина полосы промежуточной частоты (ПЧ) мала по сравнению с частотой
гетеродина. Тогда (18)
будет иметь вид:
,
т.к. ширина полосы промежуточной частоты (ПЧ) мала по сравнению с частотой
гетеродина. Тогда (18)
будет иметь вид:
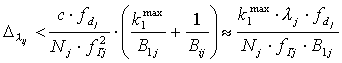 ,
(19)
,
(19)
т.е. можно считать, что погрешность определения длины волны практически не зависит от базы Bi.
Рассмотрим погрешности, обусловленные неточностью монтажа элементов решетки:
Поскольку, как указывалось выше,
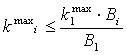 ,
а
,
а
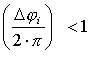 ,
то
,
то
Результаты имитационного моделирования с использованием реальных параметров показали высокую точность оценки пеленга с использованием данного алгоритма и полностью подтвердили проведенные теоретические расчеты.
3. Оценка угла прихода сигнала методом максимального правдоподобия
Статистические характеристики выборки оценок разностей фаз позволяют в рамках выбранной модели решить задачу синтеза алгоритма, который обеспечит оптимальную оценку угла прихода. Синтез будем производить методом максимального правдоподобия [4].
Пусть имеется выборка оценок фаз
![]() ,
полученная методом ДПФ, где
N
– число баз. Требуется найти такое значение оценки угла прихода, которое
максимизирует функцию правдоподобия. Имеется теоретическая зависимость фаз,
полученных на каждой базе
Bi
(4),
откуда получается
,
полученная методом ДПФ, где
N
– число баз. Требуется найти такое значение оценки угла прихода, которое
максимизирует функцию правдоподобия. Имеется теоретическая зависимость фаз,
полученных на каждой базе
Bi
(4),
откуда получается
Можно принять, что каждая такая оценка фазы имеет нормальное распределение с плотностью
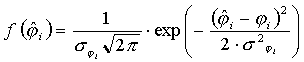 ,
(23)
,
(23)
где
![]() -
дисперсия оценок по измерениям.
-
дисперсия оценок по измерениям.
Если принять, что все оценки фаз
получены с одинаковой точностью, то их дисперсия будет всюду одинакова:
![]() .
.
Совместное распределение наблюдений,
рассматриваемое как функция неизвестного параметра
![]() ,
называется функцией правдоподобия выборки
[4]:
,
называется функцией правдоподобия выборки
[4]:
![]() ,
,
где
![]() обозначает
условную плотность непрерывного распределения. Согласно принципу максимума
правдоподобия, в качестве оценки
обозначает
условную плотность непрерывного распределения. Согласно принципу максимума
правдоподобия, в качестве оценки
![]() следует
взять такое значение
следует
взять такое значение
![]() из
области допустимых значений, для которого функция правдоподобия принимает
максимальное значение
[4].
из
области допустимых значений, для которого функция правдоподобия принимает
максимальное значение
[4].
Так как все измерения фаз независимы, то функция правдоподобия угла прихода может быть представлена в следующем виде:
Для нахождения оптимальной оценки угла
прихода
![]() по
множеству измеренных значений частичной фазы необходимо соблюдение следующих
условий максимума функции правдоподобия
[4]:
по
множеству измеренных значений частичной фазы необходимо соблюдение следующих
условий максимума функции правдоподобия
[4]:
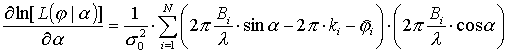
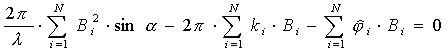
Таким образом, выражение, дающее оптимальный
алгоритм оценки угла прихода сигнала
![]() по
выборке оценок фаз
по
выборке оценок фаз
![]() ,
будет выглядеть следующим образом:
,
будет выглядеть следующим образом:
Однако, непосредственное применение такой
оценки неприемлемо, поскольку для ее вычисления необходимо знать коэффициенты
неопределенности фаз ki для каждой из баз. Следовательно, вначале
должна быть решена задача нахождения величин коэффициентов ki для
устранения неопределенности в измерении полной фазы
![]() ,
алгоритм решения которой изложен выше.
,
алгоритм решения которой изложен выше.
1. В.Б. Пестряков «Фазовые радиотехнические системы», М., «Советское радио», 1968
2. Л.М. Гольденберг, Б.Д. Матюшкин, М.Н. Поляк «Цифровая обработка сигналов», М., «Радио и связь», 1985
3. В.Н. Васильев, И.П. Гуров «Компьютерная обработка сигналов в приложении к интерферометрическим системам», С – Пб, BHV, 1998
4. М. Кендалл, А. Стюарт «Статистические выводы и связи», М., «Наука», 1973
|
|
|