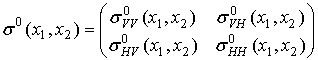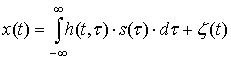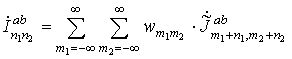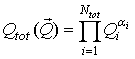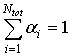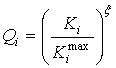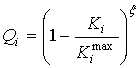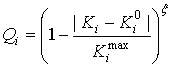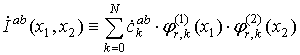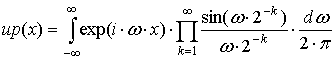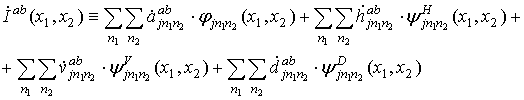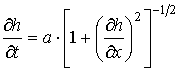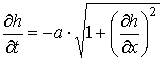Концептуальное проектирование радиолокационной станции с синтезированием апертуры антенны (РСА) на воздушном носителе "из первых принципов".

КОНЦЕПТУАЛЬНОЕ ПРОЕКТИРОВАНИЕ РАДИОЛОКАЦИОННОЙ СТАНЦИИ С СИНТЕЗИРОВАНИЕМ АПЕРТУРЫ АНТЕННЫ (РСА) НА ВОЗДУШНОМ НОСИТЕЛЕ «ИЗ ПЕРВЫХ ПРИНЦИПОВ»

А. Э. Рассадин

НРО НТОРЭС им. А. С. Попова

Получена 12 декабря 2011 г., после доработки 10 января 2012 г.

Аннотация. В работе обсуждается методология концептуального критерии качества проектирования — и для РСА как системы в целом, и для проектирования РСА на воздушном носителе в рамках парадигмы математической технологии, причём акцент делается на физических, а не на феноменологических моделях. Введены её подсистемы. Рассмотрено приближение матрицы УЭПР по данным дистанционного зондирования с помощью двумерных атомарных интерполянтов, двумерных атомарных вейвлетов Кравченко и двумерной обобщённой теоремы Котельникова с векторно-параметрическими атомарными функциями. С помощью теории роста поверхностей и классической задачи о дифракции плоской электромагнитной волны на клине построены точно решаемые модели электродинамических свойств подстилающих поверхностей в холодных регионах нашей планеты.

Ключевые слова: концептуальное проектирование, системный анализ, математическая технология, критерий качества, физическая теория дифракции, атомарные функции, РСА, радиолокационное изображение, метод характеристик, удельная эффективная поверхность рассеяния.

Abstract. In this paper methodology of conceptual design of airborne radar with synthetic aperture antenna (SAR) in the framework of mathematical technology paradigm is under investigation, moreover main attention is paid to physical but not phenomenological models. Performance criterions of design for SAR as a whole system and for its subsystems have been introduced. Approximation of specific effective dispersion section matrix on remote sensing data by means of two-dimensional atomic interpolants, two-dimensional atomic Kravchenko wavelets and two-dimensional generalized Kotelnikov theorem with vector-parametric atomic functions is considered. On the basis of the theory of growing interfaces and the classical problem on diffraction of plane electromagnetic wave by wedge exactly solved models of electrodynamic properties of surfaces in cold regions of the Earth are constructed.

Keywords: conceptual design, system analysis, mathematical technology, performance criterion, the physical theory of diffraction, SAR, radar image, atomic functions, method of characteristics, specific effective dispersion section.

All things are, but only in conception

Епископ Беркли

Введение

В настоящее время развитие производительных сил человечества достигло такого масштаба, когда они оказывают заметное влияние на окружающую среду. Это влияние приводит к нарушению энергетического, химического и биологического балансов природных систем [1-3], и, тем самым, ставит перед мировым сообществом вопрос об оценке результатов антропогенного воздействия на нашу планету в ближайшей, среднесрочной и долгосрочной перспективе [4,5]. Однако применение традиционных детерминистских математических методов для описания коэволюции биосферы и техносферы выявило их существенную ограниченность, потому что выделение того или иного объекта исследования в данной проблеме является весьма нетривиальной задачей [1–3], поскольку он всегда представляет собой некоторый элемент системы более высокого уровня, и далеко не всегда есть уверенность в том, что ее реакция на поведение изучаемого объекта будет пренебрежимо мало сказываться на его состоянии и поведении. Биосфера как совокупность взаимодействующих между собой океана, морского льда, атмосферы и биоты представляет собой существенно нелинейную систему с многочисленными механизмами положительной и отрицательной обратной связи, способную при наличии малых возмущений к кардинальным перестройкам своей структуры, причём даже без интенсивных внешних воздействий [2-5]. Выяснилось, что биота играет роль универсального регулятора, способного поддерживать состояние биосферы или ее частей, содержащих элементы биотической природы, в довольно жестких границах, несмотря на то, что антропогенные и геофизические (вулканические, космические и. т. п.) влияния могут достигать катастрофических масштабов [6]. Техносфера состоит из энергетических, промышленных, транспортных и инфотелекоммуникационных систем, обладающих сложной иерархической структурой, наличием глобального и локальных критериев качества, характеризующих работу их подсистем, существованием каналов обратной связи, квазиавтономностью подсистем и. т. д. [1]. Очевидно, что функционирование техносферы тесно связано с состоянием финансовой системы, которая, подобно биоте, также является своего рода регулятором.

Полное представление об истинном состоянии окружающей среды для обеспечения устойчивого развития нашей планеты и уменьшения опасности техногенных, природных и экологических катастроф мы можем составить, дополняя результаты моделирования биосферы данными мониторинга природных и технических объектов средствами дистанционного зондирования Земли (ДЗЗ) [7]. С начала этого века мировое сообщество стало рассматривать проекты создания всеобъемлющего, интегрированного и стабильного гражданского комплекса наблюдения за Землей [8]. Любая подобная система состоит из датчиков ДЗЗ и интеллектуальной подсистемы, обрабатывающей информацию от них [7,8], то есть является сложной технической системой. Примером такого проекта является проект Международной аэрокосмической системы мониторинга глобальных геофизических явлений и прогнозирования природных и техногенных катастроф (МАКСМ), активно пропагандируемый сейчас филиалом ФГУП «ГКНПЦ им. М. В. Хруничева» — НИИ космических систем им. А. А. Максимова [9].

Инструментом решения проблем обозначенного выше уровня сложности является системный анализ. Системный анализ — это подход к изучению объектов различной природы, представляющий собой последовательность действий по установлению структурных связей между переменными или элементами объекта исследования, то есть рассмотрение его как системы. Основным понятием системного анализа является понятие процесса. В центре методологии системного анализа находится операция количественного сравнения альтернатив, которая выполняется с целью выбора альтернативы, подлежащей реализации [10-15]. Как научное направление системный анализ был сформирован во второй половине прошлого века исследователями разных специальностей: биологом Л. фон. Берталанфи [10], физиком С. П. Никаноровым [11], философом Р. Акоффом [12], математиком М. Месаровичем [13] и др.

Системный анализ доказал свою эффективность при реализации программ освоения космоса, в экономике, в образовании и. т. д. [14,15]. Однако помимо многочисленных достоинств у системного анализа есть один существенный недостаток, а именно, в нём нет средств для изучения сложных предметных областей. Такая ситуация обусловлена отсутствием раскрытия системообразующего фактора, что не дает возможности установить изоморфность между явлениями различного класса [16].

Выход из этого методологического тупика даёт концептуальное проектирование [17], потому что система информации о мире представляет собой концептуальную систему, то есть систему определенных концептов, представлений человека о мире [18,19]. Образование концептов возникает благодаря тому, что человек вынужден адекватно отражать факты действительности в своем сознании, без чего невозможна реальная ориентация человека в мире и познание им этого мира [18,19]. Таким образом, концептуальное проектирование системы — это стадия, на которой принимаются определяющие ее последующий облик решения на различных системных уровнях, проводится исследование созданных решений и их предварительное согласование [17]. Концептуальное проектирование охватывает любой род деятельности — от систем организационного управления [20] до медицины [21] и судостроения [22], выявляя в нём закономерности и взаимосвязи с целью их более эффективного использования.

Одним из последних примеров применения концептуального проектирования является проект «Абсолютная валюта» [23], в архитектуре которого отражён опыт внедрения в России систем сотовой связи. Начальный этап реализации этого проекта заключался в создании программно-аппаратного комплекса, представляющего собой сеть серверов со специальным программным обеспечением, расположенных по всему миру. Этот комплекс в автоматическом режиме круглосуточно обеспечивает на основе предсказания валютных трендов с помощью методов цифровой обработки сигналов покупку и продажу разных видов валют, получая при этом прибыль на курсовой разнице [24], и представляет собой типичную ГРИД-систему [25], реализованную в сети Интернет на проблемно-ориентированной платформе MetaTrader [24]. Сейчас проект «Абсолютная валюта» трансформируется в интеллектуальную систему [26] (под интеллектуальной системой понимается объединенная информационным процессом совокупность технических средств и программного обеспечения, способная на основе сведений и знаний при наличии мотивации синтезировать цель, принимать решение к действию и находить рациональные способы достижения цели [27]).

Возвращаясь к проблеме разработки системы мониторинга биосферы под современным антропогенным воздействием, следует заметить, что информационная система наземного сегмента этого комплекса уже реализована «в железе» в проекте «Абсолютная валюта», и для адаптации проекта «Абсолютная валюта» к проблематике устойчивого развития нашей планеты достаточно датчики финансового поля заменить на датчики ДЗЗ. Важной разновидностью таких датчиков являются радиолокационные станции с синтезированием апертуры антенны (РСА), которые позволяют получать радиолокационные изображения (РЛИ) земной поверхности и находящихся на ней объектов независимо от метеорологических условий и уровня естественной освещенности местности [8]. Авиационные комплексы ДЗЗ имеют ряд преимуществ по сравнению с космическими ввиду значительно меньшей стоимости и более широкого возможного круга решаемых задач, причём для регионального геосистемного мониторинга размещение РСА на воздушных носителях (ВН) даже более перспективно, чем их размещение на искусственных спутниках Земли [8]. РСА на ВН как элемент такого комплекса представляет собой пример сложной технической системы, поэтому концептуальное проектирование оказывается весьма конструктивным подходом к созданию РСА на ВН [28].

1. Инструментарий концептуального проектирования РСА на ВН

Исходным пунктом концептуального проектирования является задание в той или иной форме первоначального представления о предметной области, определение её границ и подходов к её исследованию [17,20]. Как правило, предметную область нельзя описать одной математической моделью, поэтому при концептуальном проектировании на передний план выступает не изучение частных теорий предметной области, а изучение взаимоотношений между этими последними, то есть перед исследователем встаёт задача построения теории предметной области [17,20].

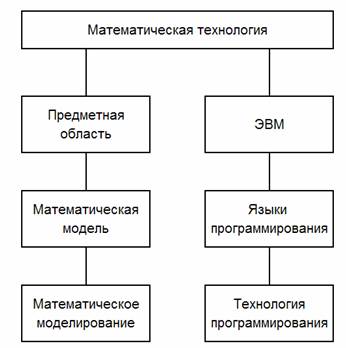
Рис. 1. Структура парадигмы математической технологии.

В случае концептуального проектирования РСА на ВН предметная область включает в себя следующие разделы физики и техники [8, 28-30]:

• электродинамику — в части задач дифракции электромагнитных волн на подстилающей поверхности, проблем распространения радиоволн, электромагнитной совместимости приёмников и передатчиков с учётом влияния корпуса ВН РСА, проектирования элементов приёмно-передающего тракта (антенн, фазированных антенных решёток, ламп бегущей волны и. т. д);

• механику — в части динамики и аэродинамики ВН РСА, а также задач теории пластин и оболочек при оценке влияния упругих колебаний конструкции ВН РСА на качество РЛИ;

• цифровую обработку сигналов — в части фильтрации эхосигнала РСА, сжатия РЛИ при передаче его на землю, контурной и структурной обработки РЛИ при его вторичной обработке на земле для распознавания необходимых объектов и пр.

Рабочим инструментом концептуального проектирования РСА является парадигма математической технологии [30,31], объединяющую две иерархические цепочки: первая цепочка включает в себя предметную область, математические модели и математическое моделирование; вторая цепочка состоит из ЭВМ, языков программирования и технологии программирования (рис. 1). Само понятие «математическая технология» возникло в СССР в начале 70-х годов прошлого века в работах А. А. Самарского, Н. Н. Яненко, К. И. Бабенко, А. Н. Панченкова и др. [32,33] как научное направление, связанное с разработкой и функционированием программных систем поддержки процессов принятия решений, в том числе с применением суперкомпьютеров. С практической точки зрения разработка математической технологии — это создание программного продукта на основе различных видов знаний.

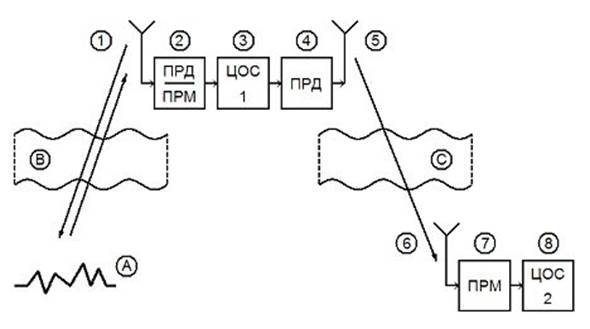
sar_math_techn

Рис. 2. Структурная схема концептуального проектирования РСА.

Основная цель концептуального проектирования РСА на ВН — создание виртуальной РСА на ВН для имитации на компьютерных моделях процесса проектной разработки в полном объеме, включая виртуальные испытания РСА на ВН в модельных средах [34,35].

Структурная схема концептуального проектирования РСА на ВН, обусловленная точным пониманием предметной области, представлена на рис. 2 (цифровые и буквенные номера блоков на рис. 2 означают математические модели подсистем РСА). Здесь 1 — модель антенны РСА; 2 — модель приёмопередатчика РСА; 3 — модель цифрового «ядра» РСА, в котором формируется и затем сжимается для передачи на землю первичное РЛИ; 4 — модель передатчика РЛИ на землю; 5 — модель антенны передатчика РЛИ на землю; 6 — модель приёмной антенны на земле; 7 — модель приёмника РЛИ на земле; 8 — модель вторичной обработки РЛИ. Таким образом, с точки зрения системного анализа окружающей средой для РСА на ВН являются подстилающая поверхность (ПП), атмосфера и сам ВН.

Достоинством этой схемы является её инвариантность относительно типа ВН РСА — самолёта, вертолёта, беспилотного летательного аппарата и. т. д.: ВН «входит» в неё только системой автоматического управления, моделью траекторных нестабильностей и спектром частот упругих колебаний своей конструкции. Кроме того, представленная на рис. 2 структура РСА позволяет учитывать влияние траекторных нестабильностей и упругих колебаний конструкции ВН РСА на качество РЛИ не только в части тракта 1 – 2 – 3 (как это обычно делается), но и в части тракта 4 – 5 – 6 – 7 (что обычно не принимается во внимание).

Виртуальные испытания РСА обеспечиваются благодаря выбору математических моделей свойств ПП (блок A на рис. 2), свойств атмосферы на рабочей частоте РСА при прохождении сквозь неё падающего и отражённого сигнала РСА (блок B на рис. 2), свойств атмосферы как широкополосной радиолинии (блок С на рис. 2) и траекторных нестабильностей ВН РСА (блок 3 на рис. 2).

Модель блока A представляет собой совокупность эффективных сечений рассеяния ПП для основных и перекрёстных поляризаций — матрицу удельных эффективных поверхностей рассеяния (УЭПР) [29]:

, (1)

где координаты — азимут и наклонная дальность, принадлежащие двумерной области , на которой формируется РЛИ, а индексы и обозначают волны горизонтальной и вертикальной поляризации соответственно (первый индекс — поляризация принимаемых колебаний, второй — излучаемых).

Модель блока B — это теория распространения плоской электромагнитной волны в случайной среде в пределах прямой видимости [36, 37], но ввиду небольшой протяжённости трассы волны в случае зондирования (в отличие от связных задач) при проектировании РСА на ВН эта развитая теория, как правило, не используется. Вместо этого анализируется автокорреляционная функция эхосигнала РСА [37]:

, (2)

где — это усреднение по ансамблю, а точка сверху означает перенос сигнала на нулевую частоту после прохождения фазовых детекторов в блоке 2. Однако следует отметить, что тройная автокорреляционная функция [38-40]:

. (3)

отражает не только амплитудные, но и фазовые соотношения в спектре , и, таким образом, даёт гораздо больше информации о влиянии турбулентной атмосферы на эхосигнал, проходящий через неё.

Моделью блока C является модель системы передачи дискретных сообщений с учётом рассеяния в канале связи [38,41]:

, (4)

где — излучаемый антенной 5 сигнал, — принимаемый антенной 6 сигнал, — импульсная характеристика канала связи, — гауссовский дельта-коррелированный шум. Сигнал представляет собой сформированное в блоке 3 закодированное и сжатое первичное РЛИ , а из сигнала на выходе блока 7 получается РЛИ , полученное на земле. Причём, вообще говоря, (индексы и , как и в формуле (1), пробегают значения и ).

Влияние траекторных нестабильностей ВН на эхосигнал РСА в блоке 3 может быть описано следующей моделью, введённой в работе [42]:

, , (5)

где — функция помеховой модуляции, в которой и — частота и безразмерная амплитуда малых колебаний ВН РСА вокруг курсового направления, — идеальный эхосигнал РСА, соответствующий боковому обзору при равномерном прямолинейном движении ВН РСА, — комплексный гауссовский шум, — интервал синтеза (более сложные модели траекторных нестабильностей ВН рассмотрены в статьях [43-45] ) .

Интересно отметить разноплановость влияния одного и того же свойства среды — турбулентности атмосферы [8,28,36,37] — на модели (4) и (5). В первом случае (модель блока С) турбулентность атмосферы непосредственно влияет на сигнал и аддитивно, и мультипликативно — через импульсную характеристику канала связи . В первом случае (модель траекторных нестабильностей ВН в блоке С) влияние турбулентности атмосферы на сигнал опосредовано — через систему автоматического управления ВН — и аддитивно.

Простейшая модель блока 8 — это сглаживание принятого на земле первичного РЛИ двумерным весовым окном для подавления спекл-шума и аддитивных помех [29,38,46]:

, (6)

где — вторичное РЛИ.

Подчеркнём, что концептуальное проектирование ориентировано на конструирование процессов выработки решений, а не на выработку решений [17,20]. Например, смена типа зондирующего сигнала РСА с линейного частотно-модулированного сигнала на одну из разновидностей фазоманипулированных сигналов не нарушает ничего в общей схеме на рис. 2 и иерархии моделей (1) – (6).

Компьютерная цепочка математической технологии (рис.1) проектирования РСА на ВН в свете схемы концептуального проектирования на рис.2 становится совершенно прозрачной: для виртуальных испытаний РСА на ВН в модельных средах требуется обыкновенная ЭВМ с фон-неймановской архитектурой и системой компьютерной математики MATLAB [34,35]. Ориентация на MATLAB обусловлена наличием в этой системе как развитого инструментария цифровой обработки сигналов [47], так и пакетов расширения для создания параллельных и распределённых программ [48] с использованием средств библиотеки Message Passing Interface [25], что даёт возможность применять для вычислений при концептуальном проектировании РСА на ВН многоядерные компьютеры, кластеры и ГРИД-системы.

После того, как в ходе концептуального проектирования определён облик блоков 1-8 на рис. 2, необходимо проанализировать их стойкость к комплексным тепловым и механическим воздействиям. Для этого в соответствии с концепцией импортозамещения целесообразно применить отечественный комплекс программ САПР АСОНИКА [49,50]. Эта автоматизированная система обеспечения надёжности и качества радиоэлектронной аппаратуры представляет собой типичную математическую технологию, которая сопряжена с системой электронного документооборота, позволяющей вносить изменения в конструкторскую документацию на любом этапе изготовления и эксплуатации узлов РСА.

Таким образом, в математической технологии концептуального проектирования РСА на ВН технологией программирования является объектно-ориентрованное программирование, а языками программирования являются императивные языки программирования высокого уровня. Значимость математической технологии при концептуальном проектировании обусловлена тем, что в её формате и её инструментальными средствами реализуется механизм интеграции знаний в предметной области.

Отдельной ветвью компьютерной цепочки математической технологии является состав, объём памяти и быстродействие бортовых вычислительных средств РСА [8], т. е. параметры блока 3 на рис. 2, для обработки на борту ВН в реальном масштабе времени требуемых объёмов информации. На данный момент максимальной производительности вычислений в цифрового «ядре» РСА можно достичь, применяя гибридную архитектуру, в которой на одной плате размещены программируемые логические интегральные схемы и цифровые сигнальные процессоры [51].

2. Критерии качества концептуального проектирования РСА на ВН

Эффективность концептуального проектирования РСА на ВН можно оценить количественно с помощью мультипликативного обобщённого критерия качества [52]:

, , , (7)

причём компоненты вектора нормированных критериев качества связаны с соответствующими им размерными критериями качества по одной из следующих формул ():

, , , (8)

где — максимальное значение го критерия качества , — некоторое фиксированное значение го критерия качества [52]. Структуризация, создаваемая концептуализацией, позволяет получать осмысленные наборы переменных.

Следует отметить, что размерность вектора (или ) больше числа блоков на рис.1, потому что каждый блок может иметь по нескольку критериев качества своего функционирования. Например, для блока 3 нужно ввести два критерия качества его успешного функционирования: критерий качества компенсации траекторных нестабильностей ВН и удаления шума в отражённом сигнале (3) и критерий качества сжатия РЛИ для передачи его на землю.

Критерий выберем из энергетических соображений [53], используя обычные нормы в пространстве :

, (9)

где — сигнал, полученный из эхосигнала (5) после проведения процедур адаптивной фильтрации (алгоритм LMS) и трешолдинга [53]. Физический смысл критерия (9) прост: виртуальная линеаризация траектории ВН в цифровом «ядре» РСА, а суперпозиция алгоритма LMS и очистки от шума в рамках парадигмы системного анализа — это управляющее воздействие на входной сигнал .

Если для сжатия РЛИ применяется алгоритм, вносящий искажения при кодировании и последующем восстановлении РЛИ, то соответствующий критерий качества можно ввести из следующих соображений: пусть матрица первичного РЛИ (с общим числом элементов ) разворачивается по строкам в вектор комплексного линейного пространства с базисом . Тогда процедура сжатия состоит в использовании коэффициентов разложения по базису пространства для получения оценки (с параметром сжатия ). Выбор количества наиболее информативных коэффициентов разложения определяется минимумом среднего значения ошибки [54]:

, (10)

где усреднение производится по множеству , а — норма пространства .

Обобщённый критерий качества концептуального проектирования РСА (7) может быть дополнен ограничениями типа неравенств. Например, для того, чтобы схема на рис.1 включала в себя и сверхширокополосные (СШП) РСА, и РСА с использованием в качестве зондирующих шумоподобных сигналов на основе псевдослучайных последовательностей [38], необходимо, чтобы при условии согласования ширины полос рабочих частот элементов РСА выполнялось требование отсутствия потери информации при прохождении сигналом каждого блока РСА, то есть по формуле Шеннона [41] для максимальной скорости передачи информации по радиоканалу:

, , (11)

где — рабочая полоса частот го блока РСА, а — отношение сигнал/шум в м блоке РСА. Задача минимизации критерия (7) при условиях (11) является типичной задачей математического программирования [52,55].

Неоспоримым достоинством выбора обобщённого критерия качества концептуального проектирования РСА в виде (7) является возможность применения к нему аппарата выпуклого анализа [55] (поскольку функция — выпуклая). Это удобно, потому что аргументы выражения (7) строятся из функционалов — см., например, формулы (9) или (10). Однако главная цель при концептуальном проектировании РСА —минимизация следующего критерия качества:

, (12)

где — точное значение УЭПР (1), а — её оценка, формируемая в блоке 8 из вторично обработанного РЛИ согласно [29]:

. (13)

С точки зрения системного анализа есть не что иное как норма разности между входным и выходным сигналами системы, и именно функционал (12) диктует переход от стандартной структурной схемы РСА [56], состоящей из блоков 1 – 2 – 3, к схеме на рис.2, в которую включена система связи (блоки 4 – 5 – 6 – 7), передающая РЛИ с борта ВН на землю, и блок 8 вторичной обработки РЛИ. Конечно, система на рис. 2 — неодносвязна, но в данном случае концептуальная целостность системы важнее её пространственной целостности.

Конкретное выражение для критерия качества (12) можно строить на основе норм в различных пространствах функций [38], например, нормы в банаховом пространстве :

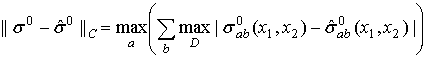, (14)

иили нормы в банаховом пространстве :

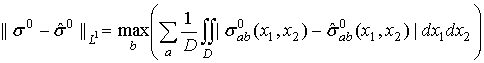, (15)

или нормы в гильбертовом пространстве :

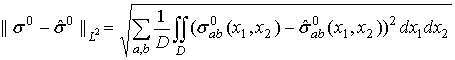. (16)

3. Способы аппроксимации вторичного РЛИ атомарными функциями

Для вычисления норм (14) - (16) необходимо уметь задавать аналитическое выражение для РЛИ по цифровым значениям вторичного РЛИ (6). Это можно сделать разными способами, однако в рамках парадигмы математической технологии целесообразно применить унифицированный подход к математическому моделированию для рассматриваемого круга проблем. В работе [30] предложено в качестве рабочего инструментария такого подхода использовать атомарные функции (АФ) Кравченко [38,57-59], поэтому опишем сначала процедуру построения гладкого вторичного РЛИ в формализме двумерных атомарных интерполянтов [58].

Пусть и область — прямоугольник. Введём на сетку , где , , , , тогда при чётном двумерный атомарный интерполянт вторичного РЛИ имеет вид [58]:

. (17)

Число членов разложения в формуле (17) , а функции выражаются через известную АФ [58,59]:

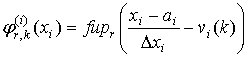, (18)

где , , а функция выражается через сплайн

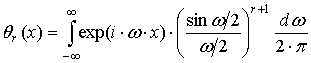(19)

и материнскую АФ [38,57-59]

(20)

с помощью операции свёртки [58]:

. (21)

Коэффициенты определяются с любой степенью точности из условий [58]:

. (22)

Другой подход к конструированию гладкого вторичного РЛИ (класса ) заключается в применении двумерных атомарных вейвлетов.

Возьмём масштабирующую функцию и материнский вейвлет , реализующие ортогональное кратномасштабное разложение , из числа атомарных вейвлетов Кравченко [57,59]. Например, можем выбрать (в частотном представлении):

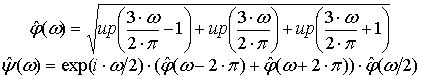, (23)

где — АФ (20). Тогда, пользуясь тем, что , и применив стандартную процедуру проектирования вектора на подпространство [47], получим:

, (24)

где базисные функции построены из функций (20) следующим образом [47]:

, (25)

а комплексные коэффициенты в разложении (24) находятся по отсчётам и коэффициентам фильтров и вейвлетов (23) с помощью двумерного обобщения алгоритма Малла [47]:

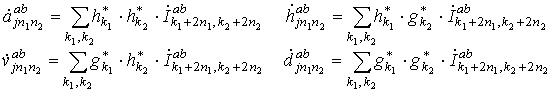. (26)

Третий способ аналитического задания вторичного РЛИ состоит в применении двумерной обобщённой теоремы Котельникова [57], а именно, если спектр сосредоточен в области , то для РЛИ справедливо разложение в ряд (подразумевается, что ):

(27)

по двумерным трансляциям функции

, (28)

где вспомогательная функция должна удовлетворять условиям:

; supp. (29)

Рассмотрим ортант в пространстве параметров и выберем эту функцию в виде:

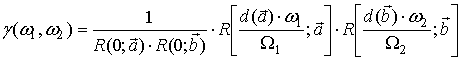. (30)

Здесь 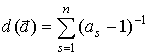, а — новая АФ, введённая в работе [60] как - кратная свёртка известных АФ [38,57-59]:

. (31)

Поскольку supp, то второе из условий (29) на функцию выполняется, поэтому по формуле (28) находим:

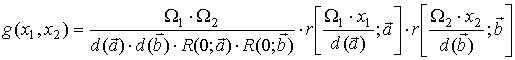, (32)

где функция есть фурье-образ АФ (31):

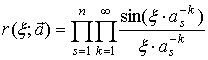. (33)

Таким образом, для зависимости вторичного РЛИ от пространственных координат может быть использовано следующее выражение:

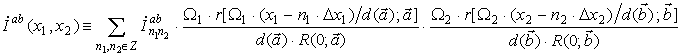(34)

Его достоинством является значительно более быстрая скорость стремления к нулю на бесконечности по сравнению с аналогичной скоростью стандартного .

Представление вторичного РЛИ аналитическими формулами (17), (24) и (34) удобно при проведении в блоке 8 его сегментации с помощью линейного интегрального оператора:

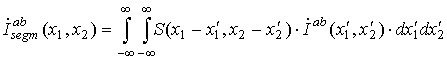, (35)

где в качестве ядра оператора сегментации можно брать не только вейвлет «мексиканская шляпа» (с параметром масштаба ) [47]:

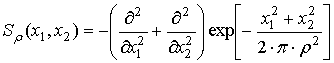, (36)

но и иные ядра, более приспособленные к оперированию с АФ.

4. Процедура построения точного решения для УЭПР

По моделям УЭПР (1) имеется обширная библиография [29,37,61]. Следует, тем не менее, отметить, что недостатком этих общепринятых феноменологических подходов является то, что ПП в них считается априори заданной. Однако в случае холодных областей нашей планеты возможно вычисление данных рассеяния «из первых принципов». Для этого рассмотрим теорию роста поверхности, предложенную в [62].

Пусть высота ПП, неограниченно простирающейся вдоль оси , задаётся функцией . Введём поле наклонов [62]:

, (37)

связанное с углом направления роста ПП в данной точке соотношением:

, (38)

тогда динамика роста ПП описывается нелинейным дифференциальным уравнением в частных производных первого порядка [62]:

, (39)

дополненным начальным условием:

. (40)

Анизотропия роста ПП учитывается в (39) зависимостью скорости роста от поля наклонов [62]. Конструктивно эта функция получается из диаграммы направленности , задающей интенсивность потока частиц, падающих на ПП под углом к оси :

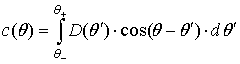(41)

(пределы интегрирования в (41) отражают эффект затенения исследуемого элемента кривой остальной её частью, после вычисления скорость роста (41) пересчитывается от угла к полю наклонов по формуле (38)).

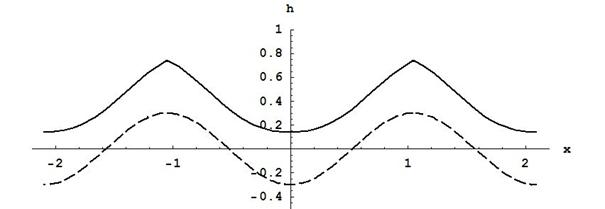
IRE_2011_1

Рис. 3. Динамика роста высоты снежного покрова.

В рамках модели (37)-(41) рассмотрим динамику формирования снежного покрова. В случае, когда , рост высоты снега описывается уравнением [63]:

, . (42)

Его решение методом характеристик с начальным условием (пунктир на рис. 3)

, (43)

задаётся неявным образом ( — лагранжева координата, ) [63]:

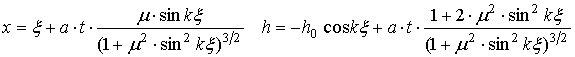. (44)

Из рис. 3, построенного по формулам (44) с помощью системы компьютерной математики Mathematica видно, что вершины со временем заостряются, а впадины становятся плоскими (сплошная линия на рис. 3).

Далее, изотропное таяние снега описывается уравнением [63]:

. (45)

Эволюция гармонического возмущения плоской ПП (пунктир на рис. 4):

(46)

в этом случае определяется как [63]:

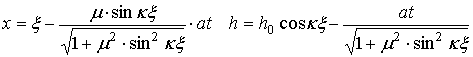(47)

И в этом случае выражения (47) с течением времени демонстрируют заострение вершин и уплощение впадин начального условия (46) (сплошная линия на рис. 4).

Таким образом, анализ решений уравнений (42) и (45), описывающих форму ПП в холодных регионах Земли, показывает, что её можно аппроксимировать периодической последовательностью одинаковых клиньев (с ребром вверх). Следовательно, в случае, когда высота клина , для нахождения матрицы УЭПР (1) применимо точное решение классической задачи дифракции плоских электромагнитных волн на идеально проводящем клине [64] (при этом, очевидно, пространственный период у исходной ПП должен быть достаточно большим).

fig_3

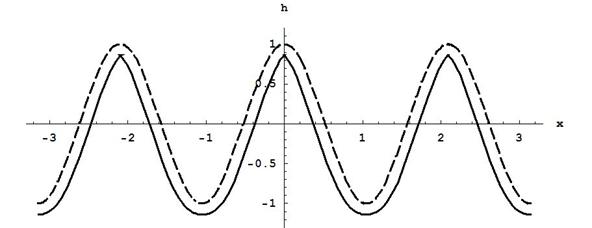
Рис. 4. Динамика таяния снежного покрова.

Рассмотрим простейшую ситуацию: ВН РСА летит строго параллельно ребру клина и осуществляет боковой обзор. Тогда для линейно поляризованной монохроматической волны с комплексной амплитудой , падающей на клин с направления ( и — полярные координаты в плоскости , ось направлена вдоль ребра клина, ), получим следующие отражённые от ПП волны [64]: волну горизонтальной поляризации

, (48)

с комплексной амплитудой вида:

, (49)

выражающейся через известную функцию [64]:

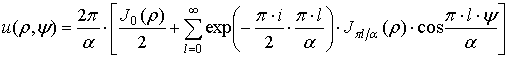(50)

( — угол клина, — функции Бесселя), и волну вертикальной поляризации

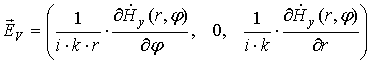, (51)

где комплексная амплитуда магнитного поля есть [64]:

. (52)

Суммируя вклады от каждого клина, с помощью формул (48) - (52) можно вычислить полное электромагнитное поле, рассеянное ПП рассмотренного вида, и, тем самым, определить матрицу УЭПР (1). Основные свойства УЭПР могут быть выяснены, если использовать известные асимптотические разложения вспомогательной функции (50) , а именно, лучевые асимптотики Зоммерфельда или асимптотики Паули [64].

Описанное выше явление заострения нелинейных волн предельной амплитуды, а, значит, и предложенная выше методика расчёта УЭПР, обладают универсальностью, поскольку для волн на воде этот эффект также имеют место.

Рассмотрим модельное интегродифференциальное уравнение Уизема [65] для скорости гидродинамической волны с пространственным периодом :

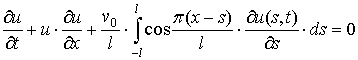, . (53)

Оно имеет точное решение — бегущую волну:

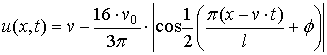, (54)

где — скорость волны, — постоянная фаза [65]. Поскольку поле скоростей волны линейно связано с высотой свободной поверхности жидкости, то выражение (54) показывает, что эта нелинейная волна имеет предельную амплитуду, причём гребень этой волны заостряется на вершине и имеет симметричную пикообразную форму.

В общем двумерном случае динамика высоты снежного покрова (здесь — двумерный вектор в горизонтальной плоскости) описывается уравнением, аналогичным уравнениям (42) или (45), например, для случая изотропного роста ПП [63]:

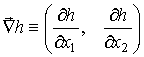, , (55)

с начальным условием

. (56)

В малоугловом приближении () уравнение (55) сводится к следующему:

. (57)

Его решение получается методом характеристик [63]:

, (58)

где — двумерный вектор лагранжевых координат.

Начиная с некоторого момента времени однозначность отображения эйлеровых координат в лагранжевы нарушается, поэтому на больших (по сравнению с ) временах нужно строить слабые решения уравнения (57) с помощью принципа абсолютного минимума Олейник-Лэкса [63]. Однако и вблизи , и при данные рассеяния электромагнитных волн (1) на ПП могут быть легко вычислены методами физической теории дифракции [64].

Заключение

Концептуальное проектирование в рамках парадигмы математической технологии позволяет обеспечить необходимое качество проектирования РСА на ВН, свободное от дорогостоящих процедур доводки натурных образцов, и охват всех стадий разработки РСА на ВН с последующим сопровождением выпуска готового изделия. Безусловно, применение системных методов на практике дорого, потому что оно требует привлечения специалистов экстра-класса. Это привело к появлению ряда направлений, упрощающих системный подход. К таким направлениям относится морфологический метод синтеза [52], заключающийся в формировании так называемой морфологической матрицы из экспертных оценок, однозначно характеризующей внутреннюю структуру исследуемой системы, и последующей специфической обработке элементов этой матрицы. Этот метод также может быть применён к проектированию РСА на ВН [66], однако он явно проигрывает методу концептуального проектирования за счёт глубины охвата этим последним предметной области в рамках парадигмы математической технологии. Поскольку проектирование РСА на ВН является сложной междисциплинарной проблемой, решение которой осуществляется большими коллективами исследователей с широкомасштабным использованием систем автоматизированного проектирования [56], то концептуальное проектирование необходимо применять также для построения системы организационного управления [11,17,20] научно-исследовательскими и опытно-конструкторскими работами инженеров и учёных, задействованных в создании РСА на ВН. Это даёт возможность организовать дееспособную коллаборацию специалистов в различных разделах рассматриваемой предметной области на период создания нового типа РСА на ВН из представителей вузов, институтов РАН и федеральных научно-производственных центров, и в конечном итоге приведёт к снижению финансовых и временных затрат на разработку и выпуск готового изделия за счёт ликвидация ненужных посредников и выполнению технического задания меньшими силами более высокой квалификации.

Особо отметим, что парадигма математической технологии стимулирует развитие современной математики. В качестве примера можно привести «слепую проблему» (4), возникающую при передаче РЛИ с борта ВН на землю, продвижение в решении которой было обусловлено достижениями в алгебраической геометрии [38].

Несомненно, создание перспективных систем ДЗЗ, особенно с комплексированием активных и пассивных радиолокационных датчиков [8, 29], должно опираться на методологию концептуального проектирования. При этом отдельным вопросом системного анализа является прогноз развития аппаратуры ДЗЗ в среднесрочной перспективе [8,9]. Понятно, что оно определяется в основном эволюцией элементной базы [67], причём не только активной, но и пассивной [68]. Также ясно, что выбор элементной базы РСА диктуется стремлением разработчиков увеличить её разрешающую способность [8,29,38]. Один из путей решения этой проблемы — применение СШП-сигналов [8,38]. Для создания СШП РСА помимо разработки аккуратных методик расчета прохождения СШП-сигналов через полупроводниковые элементы тракта РСА (рис.2) [69] необходимо совершенствовать не только технологии получения резких p-n переходов, но и методы их математического моделирования [70].

Подчеркнём, что перечень физических величин (температура моря, концентрация в атмосфере углекислого газа, площадь ледового покрова и. т. д.), которые измеряет обсуждаемый в этой работе комплекс мониторинга природных и технических объектов средствами ДЗЗ, также должен выбираться с позиций системного анализа, потому что эти данные должны служить начальными и граничными условиями глобальных моделей биосферы под воздействием антропогенных возмущений [1-7], а также получаться с минимально возможными затратами [8,9].

Описанный в Введении проект «Абсолютная валюта» также должен найти себе применение в рассмотренной области, потому что поскольку комплексы мониторинга с использованием РСА на ВН применяются в таких важных для жизни людей сферах, как сельское хозяйство, землепользование, контроль водных ресурсов и. т. д. [7-9,29,38,56], и естественным образом возникает требование независимости работ по ДЗЗ от колебаний курсов валют на мировом рынке [71]. А проблема безинфляционности активов участников рынка потребителей и поставшиков услуг ДЗЗ очевидным образом сводится к проблеме прогнозирования их поведения на валютной и фондовой биржах [24,26].

Предложенный в данной работе подход к проектированию РСА на ВН без существенных изменений переносится на проектирование РСА на космическом носителе [72], а также применим при разработке гидролокаторов с синтезированием апертуры антенны [73].

Результаты работы доложены на V Всероссийской научно-технической конференции «Радиолокация и радиосвязь», Москва, Институт радиотехники и электроники им. В. А. Котельникова РАН, 21-25 ноября 2011 г. [74].

Литература

1. Форрестер Д. Мировая динамика. — М.: АСТ, 2003. – 384 стр.

2. Моисеев Н. Н., Александров В. В., Тарко А. М. Человек и биосфера. Опыт системного анализа и эксперименты с моделями. — М.: Наука, 1985. – 271 стр.

3. Крапивин В. Ф., Свирежев Ю. М., Тарко А. М. Математическое моделирование глобальных биосферных процессов. — М.: Наука, 1982. – 278 стр.

4. Пархоменко В. П. Моделирование и прогнозирование глобальных климатических и биосферных процессов // Труды IV Всероссийской научной конференции "Математическое моделирование развивающейся экономики, экологии и биотехнологий" ЭКОМОД-2009. — Киров: 2009. C. 277 - 295.

5. Дао Минь Нгок, Пархоменко В. П. Численные эксперименты по определению влияния антропогенных и естественных факторов на климат // Труды VI Всероссийской научной конференции "Математическое моделирование развивающейся экономики, экологии и биотехнологий" ЭКОМОД-2011. — Киров: 2011. C. 279 - 291.

6. Моисеев Н. Н. Биота как регулятор и проблема sustainability // Журнал вычислительной математики и математической физики. 1994. Т. 34. Т 4. С. 533 – 544.

7. Крапивин В. Ф. Проблемы мониторинга. — М.: Знание, 1991. – 64 стр.

8. Аэрокосмический радиолокационный мониторинг Земли / Под ред. А. И. Канащенкова. — М.: Радиотехника, 2006. – 240 стр.

9. В. А. Меньшиков, С. В. Пушкарский и др. Система организации и технического обеспечения контроля природных и техногенных процессов и оперативного оповещения об их опасных проявлениях с использованием космических средств как актуальный объект внедрения экспертных систем // Интеллектуальные системы: Труды Девятого международного симпозиума / Под ред. К. А. Пупкова. — М.: РУСАКИ, 2010. С. 393 - 398.

10. Берталанфи Л. фон. История и статус общей теории систем. В кн.: Системные исследования. Методологические проблемы. Ежегодник. — М.: «Наука», 1973. С. 20 - 37.

11. Никаноров С. П. Системный анализ: этап развития методологии решения проблем в США // В кн.: Оптнер С. Л. Системный анализ для решения деловых и промышленных проблем. — М.: Советское радио, 1969. – 216 стр. С. 24 -25.

12. Акофф Р., Эмери Ф. О целеустремленных системах. Пер. с англ. — М.: Сов. радио, 1974. – 272 стр.

13. Месарович М., Мако Д., Такахара И. Теория иерархических многоуровневых систем. — М.: Мир, 1973. – 344 стр.

14. Надеев А.Т. Основы системного анализа. — Н. Новгород: ВВКЦ, 1993. – 134 стр.

15. Надеев А.Т. Задачи и упражнения по основам системного анализа. — Н. Новгород: ВВКЦ, 1992. – 68 стр.

16. Анохин П. К. Принципиальные вопросы общей теории функциональных систем. — М.: Наука, 1973. – 61 стр.

17. Никаноров С. П., Никитина Н. К., Теслинов А. Г. Введение в концептуальное проектирование АСУ: анализ и синтез структур. — М.: Изд-во РВСН, 1995. – 234 стр.

18. Витгенштейн Л. Логико-философский трактат. — М.: Наука, 2009. – 133 стр.

19. Витгенштейн Л. Философские исследования // Новое в зарубежной лингвистике. Вып. XVI. — М., 1985. С. 79 - 128.

20. Никаноров С. П. Метод концептуального проектирования систем организационного управления и его применение // Социология: 4М. 1996. N 7. C. 29 -52.

21. Дабагов А. Р. Информатизация здравоохранения и некоторые проблемы построения интегрированных медицинских информационных систем // Журнал радиоэлектроники. 2011. N 9. — Электронная публикация на сайте: http://jre.cplire.ru/ . 57 стр.

22. Панченков А. Н., Любимов В. И. Концептуальное проектирование судов: идеология, основания и виртуальная среда. — Электронная публикация на сайте www.entropyworld.narod.ru . 2010. 15 стр.

23. Товарный знак РФ N 376494 от 08.04.2009. Правообладатель: ООО «ЭРИ». Абсолютная валюта (Absolute value money). (Приоритет от 03.07.2007 г.).

24. Миленин А. В., Рассадин А. Э. Проект «Абсолютная валюта»: грид-система автоматических торгов на валютном рынке ФОРЕКС // Труды V Всероссийской научной конференции "Математическое моделирование развивающейся экономики, экологии и биотехнологий" ЭКОМОД-2010. — Киров: 2010. C. 98 - 103.

25. Воеводин В. В., Воеводин Вл. В. Параллельные вычисления. — СПб.: БХВ-Петербург, 2002. – 608 стр.

26. Миленин А. В., Миленин Ю. В., Рассадин А. Э. Математические модели макроэкономики для проекта «Абсолютная валюта» // Труды VI Всероссийской научной конференции "Математическое моделирование развивающейся экономики, экологии и биотехнологий" ЭКОМОД-2011. — Киров: 2011. C. 261 - 268.

27. Пупков К. А., Коньков В. Г. Интеллектуальные системы. — M.: Изд-во МГТУ им. Н. Э. Баумана, 2003. – 348 стр.

28. Белоцерковский С. М., Толстов Е. Ф. Системный подход к исследованиям РЛС с синтезированной апертурой антенны // Радиотехника, 1982. Т. 37. N 6. С. 49 - 52.

29. Волосюк В. К., Кравченко В. Ф. Статистическая теория радиотехнических систем дистанционного зондирования и радиолокации / Под ред. В. Ф. Кравченко. — М.: ФИЗМАТЛИТ, 2008. – 704 стр.

30. Рассадин А. Э. Аппарат атомарных функций и R-функций как основа математической технологии проектирования РСА на воздушном носителе // Интеллектуальные системы: Труды Девятого международного симпозиума / Под ред. К. А. Пупкова. — М.: РУСАКИ, 2010. — С. 224 - 228.

31. Рассадин А. Э. Математическая технология в проектировании РЛС с синтезированием апертуры антенны на воздушном носителе // Труды V Всероссийской научной конференции «Математическое моделирование развивающейся экономики, экологии и биотехнологий» ЭКОМОД-2010. — Киров: 2010. С. 118 - 127.

32. Яненко Н. Н., Каранчук В. И., Коновалов А. Н. Проблемы математической технологии // Численные методы механики сплошной среды. 1977. Т. 8. № 3. С. 129-157.

33. Панченков А. Н., Орлов Ю. Ф. и др. Математическая технология пакета прикладных программ «Полет». — Новосибирск: Наука, Сиб. отделение, 1983. – 232 стр.

34. Рассадин А. Э., Семьянова О. А. О методике изучения РСА с помощью СКМ MATLAB // Материалы XVI Межрегиональной научно-технической конференции «Обработка сигналов в системах наземной радиосвязи и оповещения». — Пушкинские Горы – Москва: Инсвязьиздат, 2008. C. 165-168.

35. Рассадин А. Э. Потенциальная РСА на базе СКМ MATLAB // Труды XIV научной конференции по радиофизике. — Н. Новгород: Изд-во ННГУ им. Н. И. Лобачевского, 2010. C. 173 - 174.

36. Татарский В. И. Распространение волн в турбулентной атмосфере. — М.: Наука, 1967. – 548 стр.

37. Исимару А. Распространение и рассеяние волн в случайно-неоднородных средах. Т. 1, 2. — М.: Мир, 1981.

38. Цифровая обработка сигналов и изображений в радиофизических приложениях / Под ред. В. Ф. Кравченко. — М.: ФИЗМАТЛИТ, 2007. – 544 стр.

39. Рассадин А. Э., Василенко Е. В. и др. Применение биспектрального анализа для исследования отражённого сигнала в РЛС с синтезированием апертуры антенны // Труды XII научной конференции по радиофизике. — Н. Новгород: Изд-во ТАЛАМ, 2008. C. 98-100.

40. Замятина И. Н., Ирхин В. И., Рассадин А. Э. Влияние траекторных нестабильностей динамичного воздушного носителя РСА на диаграмму направленности ФАР // Материалы Международной научно-технической конференции «Информационные системы и технологии ИСТ-2008».— Н.Новгород: Изд-во НГТУ, 2008. С. 22 - 24.

41. Есипенко В. И., Зельманов С. С. Теория электрической связи. — Н. Новгород, НГТУ, 2009. – 320 стр.

42. Ирхин В. И., Рассадин А. Э. Модель учёта траекторной нестабильности динамичного воздушного носителя // Вопросы радиоэлектроники, серия РЛТ. 2008. N 3. С. 149-155.

43. Замятина И. Н., Ирхин В. И., Рассадин А. Э. Рассмотрение эффектов траекторной нестабильности динамичного воздушного носителя в рамках классической механики твёрдого тела. // Радиолокация, навигация, связь: сб. докл. XIV МНТК. - Воронеж, 2008. В 3 т., т.1. С. 1980-1987.

44. Рассадин А. Э. Непрерывное вейвлет-преобразование в анализе траекторных нестабильностей воздушного носителя РСА // Труды конференции «Телекоммуникационные и вычислительные системы». — М.: Инсвязьиздат, 2009. C. 120-124.

45. Рассадин А. Э., Василенко Е. В. и др. Эффект искажения РЛИ, обусловленный расходом горючего при полёте динамичного воздушного носителя РСА // Интеллектуальные системы: Труды Восьмого международного симпозиума / Под ред. К. А. Пупкова. — М.: РУСАКИ, 2008. С. 367-370.

46. Рассадин А. Э. Теоремы комбинаторной геометрии во вторичной обработке изображений // Радиолокация, навигация, связь: сб. докл. XVII Международной научно-технической конференции. — Воронеж, 2011. В 3 т., т.1. С. 145 - 152.

47. Смоленцев Н. К. Основы теории вейвлетов. Вейвлеты в MATLAB. — М.: ДМК Пресс, 2008. – 448 стр.

48. Оленев Н. Н., Печёнкин Р. В., Чернецов А. М. Параллельное программирование в MATLAB и его приложения. — М.: ВЦ РАН, 2007. – 120 стр.

49. Автоматизированная система АСОНИКА для проектирования высоконадежных радиоэлектронных средств на принципах CALS-технологий: Том 1. // Под ред. Ю. Н. Кофанова, Н. В. Малютина, А. С. Шалумова. — М.: Энергоатомиздат, 2007. – 368 стр.

50. Антипов А. В., Григорьев С. Н., Рассадин А. Э. Перспективы развития пакета САПР АСОНИКА // Материалы XV межрегиональной научно-технической конференции «Обработка сигналов в системах наземной радиосвязи и оповещения». — Н. Новгород – М.: Типография «Поволжье», 2007. C. 326-328.

51. Беляев А., Солохина Т., Юдинцев В. Современные устройства цифровой обработки сигналов: вместе или врозь? // ЭЛЕКТРОНИКА: НТБ. 2009. N 1. С. 28-35.

52. Воинов Б. С. Информационные технологии и системы: В 2 кн. Книга I. Методология синтеза новых решений. — Н. Новгород: Изд-во ННГУ им. Н. И. Лобачевского, 2001. – 404 стр.

53. Рассадин А. Э. О комбинированных алгоритмах компенсации траекторных нестабильностей в радиовидении // Цифровая обработка сигналов и ее применение: сб. научных трудов 13-й Международной конференции. — М.: 2011. В 2 т., т.2. С. 47 - 51.

54. Френкс Л. Теория сигналов: Пер. с англ. / Под ред. Д. Е. Вакмана. — М.: Сов. Радио, 1974. – 344 стр.

55. Магарил-Ильяев Г. Г., Тихомиров В. М. Выпуклый анализ и его приложения. — М.: Книжный дом «ЛИБРОКОМ», 2011. – 176 стр.

56. Внотченко С. Л., Достовалов М. Ю. и др. Авиационные мобильные малогабаритные радиолокаторы с синтезированной апертурой семейства «Компакт» (принципы реализации и опыт применения). [Электронный ресурс] // Журнал радиоэлектроники. - 2009. - N10. Режим доступа: http://jre.cplire.ru/jre/oct09/5/text.pdf. 16 стр.

57. Кравченко В. Ф., Кравченко О. В. и др. Атомарные функции и WA-системы функций в современных проблемах радиофизики и техники // Электромагнитные волны и электронные системы. 2011. Т. 16. № 9. С. 7 - 32.

58. Кравченко В. Ф. Лекции по теории атомарных функций и некоторым их приложениям. — М.: Радиотехника, 2003. – 512 стр.

59. Кравченко В. Ф., Юрин А. В. Новый класс вейвлет-функций в цифровой обработке сигналов и изображений // Успехи современной радиоэлектроники, 2008. N 5. C. 3 - 123.

60. Рассадин А. Э. Векторно-параметрические атомарные функции // Радиоэлектронные средства передачи и приёма сигналов и визуализации информации: Материалы Первой Всероссийской конференции. — М.: Изд-во РНТОРЭС им. А. С. Попова, 2011. С. 60 - 62.

61. Басс Ф. Г., Фукс И. М. Рассеяние волн на статистически неровной поверхности. — М.: Наука, 1972. – 424 стр.

62. Kardar M., Parisi G., Zhang Y. C. Dynamical scaling of growing interfaces // Phys. Rev. Lett. 1986. V. 56. P. 889 - 892.

63. Гурбатов С. Н., Руденко О. В., Саичев А. И. Волны и структуры в нелинейных средах без дисперсии. Приложения к нелинейной акустике. — М.: ФИЗМАТЛИТ, 2008. – 496 стр.

64. Уфимцев П. Я. Основы физической теории дифракции. — М.: БИНОМ. Лаборатория знаний, 2009. – 350 стр.

65. Габов С. А. Введение в теорию нелинейных волн. — М.: Изд-во МГУ, 1988. – 176 стр.

66. Дементьева М. Л., Рассадин А. Э. Перспективы применения морфологического метода в синтезе вертолётного комплекса мониторинга для проводки судов в арктических льдах // Сборник материалов Всероссийской научно-технической конференции «Общество, наука, инновации». В 4 т. — Киров: Изд-во ГОУ ВПО «ВятГУ», 2010. Т. 4. С. 58 – 61.

67. А. С. Бугаев, Ю. В. Гуляев и др. Микро- и наноэлектроника в системах радиолокации. [Электронный ресурс] // Журнал Радиоэлектроники. – библиотека журнала – Режим доступа: http://jre.cplire.ru/jre/library/6/index.html

68. Двоешерстов М. Ю., Рассадин А. Э. и др. Модифицированный метод расчета топологии устройств на поверхностных акустических волнах // Материалы XV межрегиональной научно-технической конференции «Обработка сигналов в системах наземной радиосвязи и оповещения».— Н. Новгород – М.: Типография «Поволжье», 2007. C. 281-286.

69. Рассадин А. Э. О некоторых особенностях прохождения СШП-сигналов через цифровые и аналоговые устройства в РСА // Цифровая обработка сигналов и ее применение: сб. научн. трудов 11-й Международной конференции // - М.: 2009. C. 342 -346.

70. Кондраченко Л. А., Рассадин А. Э., Чистяков А. С. Моделирование процесса нелинейной высокоградиентной диффузии в полупроводниках // Письма в Журнал технической физики. 2005. Т. 31. Вып. 3. C. 27-30.

71. Дементьева М. Л., Рассадин А. Э. Новые математические методы анализа мирового рынка услуг дистанционного зондирования Земли // Интеллектуальные системы: Труды Девятого международного симпозиума / Под ред. К. А. Пупкова. — М.: РУСАКИ, 2010. С. 697 – 700.

72. Рассадин А. Э. Траекторные нестабильности космического носителя РСА, обусловленные эффектами общей теории относительности // “T-Comm Telecommunications and Transport” magazine. 2009, август. Спецвыпуск «Технологии информационного общества». Часть III . С. 117-118.

73. Каевицер В. И., Смольянинов В. М., Смольянинов И. В. Интерферометрическая батиметрия широкополосным гидролокатором бокового обзора // Доклады V Всероссийской научно-технической конференции «Радиолокация и радиосвязь» — М., 2011. С. 366 – 373.

74. Рассадин А. Э. Точно решаемые модели электродинамических свойств подстилающей поверхности для концептуального проектирования РСА // Доклады V Всероссийской научно-технической конференции «Радиолокация и радиосвязь». — М.: ИРЭ им. В. А. Котельникова РАН, 2011. С. 332-337.