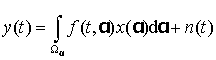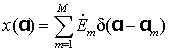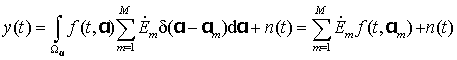УДК 621.396.962
метод повышения разрешающей способности радиолокационных систем при цифровой обработке сигналов
С. А. Климов
лаборатория проблем обработки радиолокационной
информации Военной академии войсковой ПВО
имени Маршала Советского Союза А. М.
Василевского, Смоленск
Получена 20 декабря 2012 г.
Аннотация. Предложен метод разрешения смеси неортогональных сигналов и шума в активных радиолокационных системах. Устойчивость решения задачи обеспечивается как за счет конечномерной аппроксимации оператора преобразования системы, так и модели наблюдения. Предполагается, что модель наблюдения есть ограниченная сумма проекций в подпространстве ортогональных (унитарных) матриц, функционально связанных с матрицей исходного линейного оператора преобразования системы. Представлены результаты имитационного математического моделирования метода, подтверждающие его эффективность. Материал докладывался на 6-й Всероссийской конференции «Радиолокация и радиосвязь»
Ключевые слова: разрешение, разрешающая способность, число обусловленности, матрица линейного оператора, сингулярное разложение.
Abstract. The method of permission of signals in active radar systems is offered. Stability of the decision is provided as at the expense of finite-dimensional approximation of the operator of transformation of system, and supervision model. It is supposed that supervision model an essence finite-dimensional set of projections in a subspace of the orthogonal (unitary) matrixes which have been functionally connected with a matrix of the initial linear operator of transformation of system. The results of the imitating mathematical modeling confirming high efficiency of the offered method of permission of signals are presented.
Keywords – permission, resolution, condition number, matrix of the linear operator, singular value decomposition.
Введение
Среди класса основных задач, решаемых в радиолокационных системах (РЛС) при наблюдении целей, таких как обнаружение, разрешение, измерение и классификация [1], большое значение имеет задача разрешения. Для физически реализуемых систем разрешающая способность всегда конечна. Последнее определяется технологическими и техническими ограничениями и, кроме того, физическими процессами, протекающими в них. Например, в пространственной области – это дифракционные явления, являющиеся следствием конечной ширины апертуры пространственного фильтра, во временной – конечная ширина полосы пропускания системы, в частотной – конечное время наблюдения того или иного физического процесса. Указанные ограничения на разрешающую способность для систем различной физической природы были сформулированы в классических трудах Рэлея и Ф. М. Вудворда.
Этот вывод целесообразно пояснить несколькими примерами. Известно, что при существующих принципах построения РЛС ее потенциальная разрешающая способность по дальности обратно пропорциональна ширине спектра зондирующего сигнала. Это заставляет использовать широкополосные сигналы для достижения требуемой разрешающей способности РЛС по дальности. Применение широкополосных сигналов усложняет аппаратуру, затрудняет электромагнитную совместимость РЛС, снижает помехоустойчивость РЛС военного назначения. Существуют определенные практические ограничения на использование широкополосных (многочастотных) сигналов для получения систем с высоким разрешением. Основными причинами, сдерживающими расширение спектров сигналов при модернизации существующих и проектировании перспективных РЛС, являются ограниченные возможности элементной базы по цифровой обработке сигналов, а также широкое использование активных фазированных антенных решеток с последующим выходом на цифровые.
При традиционных способах обработки сигналов в РЛС единственным средством повышения разрешающей способности по частоте является увеличение времени когерентного накопления. Однако время когерентного накопления в РЛС ограничено, с одной стороны, общим временным ресурсом (особенно в современных многофункциональных многоцелевых РЛС), а с другой – конечным интервалом когерентности эхосигналов реальных целей (влияние вторичного эффекта Доплера, «собственных шумов» целей и т. д.). Отмеченные факторы ограничивают возможность повышения разрешающей способности РЛС по частоте традиционными способами.
Как правило, еще более жесткими являются ограничения на размер антенны РЛС, что при существующих принципах обработки сигналов приводит к неприемлемо низкой разрешающей способности РЛС по угловым координатам. Вместе с тем, можно утверждать, что основные сложности при вторичной и третичной обработке радиолокационной информации также связаны с ограниченной разрешающей способностью РЛС на этапе первичной обработки.
В противовоздушном бою для эффективного решения задачи целераспределения чрезвычайно важным является определение количественного состава групповых целей, что напрямую зависит от возможностей РЛС по разрешению и селекции целей. Недостаточная разрешающая способность РЛС противовоздушной обороны не позволяет достоверно определить количественный состав групп воздушных целей, их боевой порядок, и как следствие, установить важность целей, что особенно существенно для решения задачи целераспределения.
В связи с этим поиск эффективных, экономичных в вычислительном отношении методов повышения разрешающей способности РЛС является актуальной проблемой.
Обоснование метода разрешения сигналов
Известен ряд фундаментальных работ, посвященных проблеме разрешения сигналов [2–6]. Из их анализа следует, что теория разрешения прошла в своем развитии ряд этапов. Первый этап можно назвать детерминистическим подходом. Он связан с именами Д. В. Стрэтта, лорда Рэлея (далее по тексту Рэлей) в оптике и Ф. М. Вудворда, И. Дэвиса в радиолокации [2, 3]. Рэлей заложил основы разрешения: дал ясную физическую трактовку причин ограничения разрешающей способности; сформулировал основные закономерности разрешения для прямоугольных и круглых апертур спектроскопов, а также линейных оптических решеток; исследовал некоторые способы повышения разрешающей способности; показал влияние искажений в спектроскопе и точности изготовления оптических решеток на разрешающую способность. Работы Ф. М. Вудворда и И. Дэвиса продолжили развитие основной идеи Рэлея по исследованию разрешающей способности, заключающейся в изучении характерных свойств функции отклика (реакции) системы при воздействии на ее вход суммы двух сигналов с близкими параметрами (совместной функции корреляции по времени и частоте). При этом исследованию подвергался идеальный отклик системы, поскольку точно известной считалась аппаратная функция (импульсная характеристика зондирующего сигнала) РЛС. При этом не учитывались шумы наблюдения, присутствующие в любой физической системе. Каких-либо статистических свойств такая идеальная функция корреляции не отражает.
Анализ работы Ф. М. Вудворда показал, что при рассмотрении вопроса о разрешении радиолокационных сигналов он шел по пути поиска «идеального прибора» или прибора, обладающего характеристикой преобразования (аппаратной функцией), известной точно, причем с одновременно бесконечной импульсной характеристикой и полосой пропускания. Анализ работ [2, 3] позволяет сделать следующий вывод: понятие разрешающей способности, определяемое критериями Рэлея и Вудворда, – это объективное ограничение для реальных систем, основанное на физических процессах, происходящих в них. Другим словами, критерии разрешения Рэлея и Вудворда являются величинами, характеризующими свойства физической системы (характеристики ее аппаратной функции), а не методы обработки сигналов в ней. Детерминистический подход к определению разрешающей способности был основополагающим вплоть до 50-х годов ХХ века.
С появлением новых методов обработки результатов наблюдений и достижением в ряде случаев разрешения, превышающего характеристики используемой физической системы, классическое определение разрешающей способности стало противоречить опыту. Это привело к ряду важных исследований, особенно в теории связи, радиолокации, спектрального анализа, астрономии, экспериментальной физике, результатом которых стал принципиально новый взгляд на понятие разрешающей способности. Впервые был введен статистический анализ разрешающей способности, а для исследования потенциальных характеристик разрешения стали применяться методы теории статистических решений: Байесовский и максимального правдоподобия. Второй этап можно назвать статистическим подходом к разрешению. Статистический анализ разрешающей способности предложили сразу ряд отечественных и зарубежных авторов, первыми среди которых были Я. Д. Ширман и К. Хелстром.
С именем К. Хелстрома связано появление первого алгоритма сверхразрешения, основанного на методе максимального правдоподобия [4]. Был раскрыт статистический характер разрешающей способности. К. Хелстром установил, что разрешающая способность зависит от метода обработки (анализа) сигналов. При этом им были получены показатели разрешения в виде условных вероятностей правильного обнаружения и ложной тревоги для оценок амплитуд сигналов, зависящие от отношения сигнал-шум и функции неопределенностей (аппаратной функции системы). Из анализа показателей разрешения К. Хелстрома следует, что за счет метода обработки существует принципиальная возможность преодоления разрешения, определяемого свойствами физической системы, т. е. фактически получение так называемого сверхразрешения. Таким образом, К. Хелстром предложил первый алгоритм сверхразрешения заданного числа сигналов с неизвестными параметрами, основанный на методе максимального правдоподобия теории статистических решений. Стратегия разрешения, предложенная впервые К. Хелстромом в виде сравнения с порогом амплитуд сигналов в момент максимально правдоподобных оценок неизвестных параметров этих сигналов, успешно используется в настоящее время в алгоритмах сверхразрешения при статистическом подходе.
Статистический подход к разрешению получил свое огромное развитие в работе Я. Д. Ширмана [5]. В ней наиболее полно рассмотрены виды разрешающей способности и показатели качества разрешения. При рассмотрении различных видов оптимального разрешения применяется Байесовский метод. Известно, что практическое использование такого метода наталкивается на определенные трудности. К ним можно отнести большой объем априорной информации относительно вида распределений параметров сигналов и помех, субъективный выбор функции потерь, сложность получения алгоритмов разрешения в явном виде и ряд других.
В связи с этим, в работе [6] для синтеза алгоритма разрешения сигналов применяется метод максимального правдоподобия. Из нее же следует, что начиная еще с пионерской работы по сверхразрешению К. Хелстрома, этот метод в его традиционной форме неприменим для решения указанной задачи. Поэтому разработан небайесовский метод, названный обобщенным методом максимального правдоподобия. В работе [6] в систематизированном виде предложен алгоритм разрешения неизвестного числа квазидетерминированных сигналов с постоянными на конечном интервале времени значениями параметров на фоне гауссовской помехи. Рассматривается как статистический синтез алгоритма разрешения, так и анализ качества статистических решений, формируемых таким алгоритмом. Вводятся понятия: «двухфункциональное решающее устройство» и «двухфункциональное правило выбора решения», которые выполняют одновременно две функции – различение сигналов и оценивание их параметров. По мнению автора, определение разрешающей способности, сформулированное в работе [6], в полном объеме отвечает требованиям практики и современного этапа развития статистического подхода к разрешению. Итак, под разрешением сигналов будем понимать указание числа сигналов, содержащихся в реализации смеси сигналов и помех, и оценивания параметров всех обнаруженных сигналов [6]. Этого определения мы будем придерживаться в дальнейшем.
В последнее время интенсивное развитие получили так называемые «современные» методы спектрального оценивания [7 и др.], имеющие более высокую разрешающую способность, чем «классические», за счет использования некоторой априорной информации об оцениваемом сигнале. Все методы спектрального оценивания так или иначе связаны с получением оценки прямой или обратной корреляционной матрицы входных сигналов, что требует большого объема вычислений. Последнее приводит к образованию вместе с аддитивным шумом мультипликативных шумов, снижению отношения сигнал-шум при обработке коротких последовательностей входных данных и большим вычислительным затратам.
Дальнейшим развитием статистических методов повышения разрешающей способности РЛС является проекционный метод [8]. Метод сочетает подход Петрова – Галёркина для решения операторных уравнений, а также стратегию разрешения К. Хелстрома в виде сравнения с порогом амплитуд сигналов в момент максимально правдоподобных оценок неизвестных параметров этих сигналов. Для своего использования метод требует внесения априорной физической нетривиальной дополнительной информации, с помощью которой можно исключить ложные решения и выделить решение, наиболее близкое к истинному. При этом под априорной информацией следует понимать количество, положение и форму отдельных рассеивающих элементов групповой сосредоточенной радиолокационной цели, а также вид базисных функций для их аппроксимации. Существенным препятствием на этом пути являются недостоверные, недостаточные или вообще отсутствующие такие априорные сведения, а также отсутствие методологии формирования этой априорной информации для решения практических задач. Кроме того, метод обладает большими вычислительными затратами.
Таким образом, существует проблема выбора априорной физической информации, позволяющей обеспечить устойчивость и удовлетворительную вычислительную сложность того или иного метода разрешения смеси неортогональных эхосигналов. Кроме того, проблемными моментами являются: существенное усложнение алгоритмов и резкий рост вычислительных затрат при увеличении ожидаемого количества разрешаемых сигналов (количества целей в группе). Последнее связано с тем, что при росте количества разрешаемых сигналов и, как следствие, повышении размерности пространства сигналов методы сверхразрешения требуют в сравнении с классическими методами обработки сигналов существенно более мелкого шага при вычислении целевой функции и соответственно характеризуются повышенной относительной сложностью вычислений, что ограничивает их практическое применение в РЛС.
Постановочную часть проблемы разрешения
предлагается сформулировать в следующем виде: по наблюдаемому сигналу ![]() на выходе пространственно-временной радиолокационной
системы с известным оператором преобразования
на выходе пространственно-временной радиолокационной
системы с известным оператором преобразования ![]() требуется
восстановить неизвестный эхосигнал
требуется
восстановить неизвестный эхосигнал ![]() на ее входе, сформированный
объектом радиолокации.
на ее входе, сформированный
объектом радиолокации.
Математическая интерпретация процесса
радиолокационного разрешения сигналов заключается в последовательном
преобразовании из пространства зондирующих ![]() сигналов
в пространство наблюдаемых
сигналов
в пространство наблюдаемых ![]() сигналов, поступающих
на вход устройства разрешения и, далее в пространство решений
сигналов, поступающих
на вход устройства разрешения и, далее в пространство решений ![]() . Каждый этап преобразования зондирующего
сигнала
. Каждый этап преобразования зондирующего
сигнала ![]() математически может быть представлен в
виде некоторого оператора преобразования. Качество решений
математически может быть представлен в
виде некоторого оператора преобразования. Качество решений ![]() зависит в той или иной степени от характеристик
всех операторов преобразования. Тем не менее, предметом дальнейшего детального
рассмотрения будет в основном устройство разрешения и реализуемое им с помощью
некоторого оператора преобразование пространства наблюдаемых
зависит в той или иной степени от характеристик
всех операторов преобразования. Тем не менее, предметом дальнейшего детального
рассмотрения будет в основном устройство разрешения и реализуемое им с помощью
некоторого оператора преобразование пространства наблюдаемых ![]() сигналов в пространство
сигналов в пространство ![]() решений.
решений.
Рассматривая
класс линейных систем, запишем математическую формулировку задачи разрешения
сигналов на основе оператора преобразования ![]() интегрального
типа
интегрального
типа
где ![]() – время;
– время; ![]() – вектор неизвестных параметров
эхосигнала объекта радиолокации;
– вектор неизвестных параметров
эхосигнала объекта радиолокации; ![]() – искомый неизвестный
эхосигнал, сформированный объектом радиолокации;
– искомый неизвестный
эхосигнал, сформированный объектом радиолокации; ![]() –
наблюдаемый на выходе пространственно-временной радиолокационной системы
сигнал;
–
наблюдаемый на выходе пространственно-временной радиолокационной системы
сигнал;![]() – ядро интегрального уравнения (пространственно-частотно-временной
оператор преобразования или аппаратная функция системы);
– ядро интегрального уравнения (пространственно-частотно-временной
оператор преобразования или аппаратная функция системы); ![]() – шумы наблюдения;
– шумы наблюдения; ![]() – интервал изменения переменной
– интервал изменения переменной ![]() ;
; ![]() –
область поля параметров, на которой определена функция
–
область поля параметров, на которой определена функция ![]() .
Как правило, считают, что
.
Как правило, считают, что ![]() ,
, ![]() ,
, ![]() и
и ![]() принадлежат комплексному гильбертову пространству.
принадлежат комплексному гильбертову пространству.
Предполагается,
что пространство принимаемых ![]() сигналов включает
несколько сигналов с неизвестными параметрами. В силу принципа суперпозиции
математическую модель эхосигнала группового радиолокационного объекта (РЛО)
можно представить в виде суммы неизвестного числа М точечных источников
вторичного излучения (
сигналов включает
несколько сигналов с неизвестными параметрами. В силу принципа суперпозиции
математическую модель эхосигнала группового радиолокационного объекта (РЛО)
можно представить в виде суммы неизвестного числа М точечных источников
вторичного излучения (![]() -функций):
-функций):
где ![]() – случайный комплексный коэффициент
рассеяния m-го отдельного объекта из состава группового, соответствующий точке
с вектором параметров
– случайный комплексный коэффициент
рассеяния m-го отдельного объекта из состава группового, соответствующий точке
с вектором параметров ![]() ;
; ![]() –
эхосигнал, сформированный групповым РЛО. Функция
–
эхосигнал, сформированный групповым РЛО. Функция ![]() в выражении
(2) зависит от параметров объекта радиолокации, объединенных в многомерный
вектор
в выражении
(2) зависит от параметров объекта радиолокации, объединенных в многомерный
вектор ![]() . В качестве составляющих
. В качестве составляющих ![]() m-го вектора
m-го вектора ![]() могут быть дальность, скорость, угловые координаты
и др. параметры m-го отдельного объекта, где
могут быть дальность, скорость, угловые координаты
и др. параметры m-го отдельного объекта, где ![]() , I – число параметров. Неизвестным считается и
число М эхосигналов, формирующих
, I – число параметров. Неизвестным считается и
число М эхосигналов, формирующих ![]() .
.
Из
сформулированной задачи следует, что проблему разрешения необходимо рассматривать
как проблему решения известной в математике и физике, так называемой обратной
задачи рассеяния или задачи восстановления на входе радиолокационной системы
неизвестной функции ![]() , на которую воздействует
оператор преобразования
, на которую воздействует
оператор преобразования ![]() (аппаратная функция),
основываясь при этом на результатах наблюдения функции
(аппаратная функция),
основываясь при этом на результатах наблюдения функции ![]() на
выходе системы. Фактически, анализируя
на
выходе системы. Фактически, анализируя ![]() , необходимо
построить адекватную математическую модель функции
, необходимо
построить адекватную математическую модель функции ![]() ,
непосредственно связанную с рассеивающими характеристиками объекта
радиолокации. Ключевым здесь является то, что необходимо восстановить причину
по наблюдаемому следствию [9].
,
непосредственно связанную с рассеивающими характеристиками объекта
радиолокации. Ключевым здесь является то, что необходимо восстановить причину
по наблюдаемому следствию [9].
Из выражения (1) видно, что с математической точки зрения задача разрешения сводится к решению линейного интегрального уравнения, известного как уравнение Фредгольма 1-го рода. Известно, что уравнения типа (1) относятся к некорректно поставленным задачам [10]. Принципиальная сложность, связанная с решением интегральных уравнений 1-го рода (1), заключается в том, что решения этих уравнений неустойчивы к малым изменениям входных данных [9, 10]. Последнее указывает на нарушение третьего условия корректности задач по Адамару: решение непрерывно должно зависеть от результата наблюдения, если в качестве наблюдения могут выступать произвольные непрерывные функции.
Рассмотрим модель группового РЛО в виде (2). Подстановка (2) в выражение (1) с учетом фильтрующего свойства функции Дирака дает
Ориентируясь на РЛС с цифровой обработкой сигналов и учитывая,
что сигнал ![]() всегда известен в конечном числе точек
наблюдения дискретизируем уравнение (3) на сетках
всегда известен в конечном числе точек
наблюдения дискретизируем уравнение (3) на сетках ![]() ,
, ![]() ,
, ![]() заменяя
непрерывные функции их сеточными аналогами
заменяя
непрерывные функции их сеточными аналогами
![]() ;
; ![]() ;
;
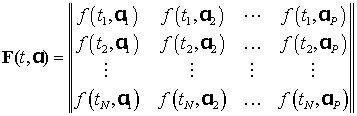 .
.
При дискретизации
предполагается, что количество отдельных объектов в составе группового
ограничено сверху числом ![]() , а их комплексные
коэффициенты рассеяния соответствуют всем точкам заданного в матрице
, а их комплексные
коэффициенты рассеяния соответствуют всем точкам заданного в матрице ![]() вектора параметров
вектора параметров ![]() ,
, ![]() . Так
как в составе реального группового РЛО может присутствовать разное количество отдельных
объектов, то отдельные элементы вектора
. Так
как в составе реального группового РЛО может присутствовать разное количество отдельных
объектов, то отдельные элементы вектора ![]() в
действительности могут быть равны нулю. В этом случае приходим к системе
линейных алгебраических уравнений (СЛАУ) вида
в
действительности могут быть равны нулю. В этом случае приходим к системе
линейных алгебраических уравнений (СЛАУ) вида
где ![]() –
– ![]() -вектор-столбец результатов наблюдения
сигнала;
-вектор-столбец результатов наблюдения
сигнала; ![]() –
– ![]() -матрица
коэффициентов оператора преобразования
РЛС;
-матрица
коэффициентов оператора преобразования
РЛС; ![]() –
– ![]() -вектор-столбец
комплексных коэффициентов рассеяния;
-вектор-столбец
комплексных коэффициентов рассеяния; ![]() –
– ![]() -вектор-столбец шумов наблюдения.
-вектор-столбец шумов наблюдения.
Рассмотрим
корректность поставленной задачи в виде СЛАУ (4). Пусть система (4) имеет решение при любой правой части
![]() . Это
значит, что вектор
. Это
значит, что вектор ![]() должен быть ортогонален ядру
матрицы
должен быть ортогонален ядру
матрицы ![]() , т. е.
, т. е. ![]() . Так
как вектор
. Так
как вектор ![]() может быть любым, то
может быть любым, то ![]() . Поэтому
. Поэтому ![]() , что выполняется,
если
, что выполняется,
если ![]() состоит только из нулевого вектора. Предположим
теперь, что существует по крайней мере одно ненулевое решение, т. е.
состоит только из нулевого вектора. Предположим
теперь, что существует по крайней мере одно ненулевое решение, т. е. ![]() состоит не только из нулевого вектора. При этом нарушается соотношение
состоит не только из нулевого вектора. При этом нарушается соотношение ![]() . Следовательно, имеется вектор
. Следовательно, имеется вектор ![]() , который не является
линейной комбинацией вектор-столбцов матрицы
, который не является
линейной комбинацией вектор-столбцов матрицы ![]() . Согласно [11] для этого вектора
. Согласно [11] для этого вектора ![]() система (4) не может
иметь решение. Таким образом, разрешимость СЛАУ (4) при любой правой части не
гарантируется. Обеспечить совместность системы (4) можно, если выполнить такое
преобразование с вектором
система (4) не может
иметь решение. Таким образом, разрешимость СЛАУ (4) при любой правой части не
гарантируется. Обеспечить совместность системы (4) можно, если выполнить такое
преобразование с вектором ![]() , которое обеспечит его
принадлежность к
, которое обеспечит его
принадлежность к ![]() матрицы
матрицы ![]() .
Такое преобразование предлагается осуществлять в виде
.
Такое преобразование предлагается осуществлять в виде ![]() ,
где
,
где ![]() – псевдообратная матрица [11, 12]. В этом случае результат векторно-матричного произведения
– псевдообратная матрица [11, 12]. В этом случае результат векторно-матричного произведения ![]() будет являться линейной оболочкой
вектор-столбцов матрицы
будет являться линейной оболочкой
вектор-столбцов матрицы ![]() и система (4) будет
совместна при любой правой части
и система (4) будет
совместна при любой правой части ![]() [11].
Следовательно, она будет удовлетворять первому
требованию корректности задачи по Адамару, а именно требованию о существовании
решения. В случае совместности системы ответ на вопрос о числе решений можно
получить из теоремы Кронекера – Капелли [11]. С одной стороны,
[11].
Следовательно, она будет удовлетворять первому
требованию корректности задачи по Адамару, а именно требованию о существовании
решения. В случае совместности системы ответ на вопрос о числе решений можно
получить из теоремы Кронекера – Капелли [11]. С одной стороны, ![]() не может превышать числа ее столбцов,
т. е. числа
не может превышать числа ее столбцов,
т. е. числа ![]() . С другой стороны,
. С другой стороны, ![]() меньше числа неизвестных, поскольку число
неизвестных параметров СЛАУ (4) при решении задачи разрешения сигналов в
радиолокационных системах может достигать
меньше числа неизвестных, поскольку число
неизвестных параметров СЛАУ (4) при решении задачи разрешения сигналов в
радиолокационных системах может достигать ![]() ,
, ![]() . В этом случае система уравнений (4)
имеет бесконечно много решений, а именно: некоторым
. В этом случае система уравнений (4)
имеет бесконечно много решений, а именно: некоторым ![]() неизвестным
можно придать произвольные значения, тогда оставшиеся
неизвестным
можно придать произвольные значения, тогда оставшиеся ![]() неизвестных
определятся уже единственным образом. В этих условиях не выполняется второе
требование корректности задачи, заключающееся в единственности ее решения.
неизвестных
определятся уже единственным образом. В этих условиях не выполняется второе
требование корректности задачи, заключающееся в единственности ее решения.
Существует
еще одна определяющая проблема: матрицы СЛАУ, получаемые в результате
дискретизации уравнения Фредгольма 1-го рода, при достаточно больших ![]() плохо обусловлены. Ключевым моментом
здесь является то, что для обеспечения высокого разрешения сигналов мы должны
устремить
плохо обусловлены. Ключевым моментом
здесь является то, что для обеспечения высокого разрешения сигналов мы должны
устремить ![]() . При этом можно было бы ожидать, что
решение
. При этом можно было бы ожидать, что
решение ![]() будет аппроксимировать истинное значение
будет аппроксимировать истинное значение ![]() в уравнении (4) с большой точностью. Однако
этого не происходит, т. к. матрица
в уравнении (4) с большой точностью. Однако
этого не происходит, т. к. матрица ![]() оператора
преобразования системы при требуемых для задач высокого разрешения параметрах
оператора
преобразования системы при требуемых для задач высокого разрешения параметрах ![]() ,
,![]() ,
, ![]() является
плохо обусловленной, а сама задача получения решения СЛАУ (3) – неустойчивой. Например, для дискретных аналогов одномерных характеристик
вида
является
плохо обусловленной, а сама задача получения решения СЛАУ (3) – неустойчивой. Например, для дискретных аналогов одномерных характеристик
вида ![]() ,
, ![]() ,
, ![]() и
составленных для них
и
составленных для них ![]() -матриц
-матриц ![]() спектральные
числа обусловленности
спектральные
числа обусловленности ![]() достигают значений
порядка 104.
достигают значений
порядка 104.
В
качестве примера на рис. 1 представлены сеточные аналоги ядер интегрального
уравнения (1), часто используемые при решении задач радиолокационного наблюдения
видов ![]() (см. рис. 1 а), главного лепестка
(см. рис. 1 а), главного лепестка
![]() (см. рис. 1 б),
(см. рис. 1 б), ![]() (см. рис. 1, слева), составленная
для них
(см. рис. 1, слева), составленная
для них ![]() -матрицы
-матрицы ![]() значений
характеристик преобразования (см. рис. 1, в центре) и их спектральные
числа обусловленности
значений
характеристик преобразования (см. рис. 1, в центре) и их спектральные
числа обусловленности ![]() (см. рис. 1, справа). Из рис. 1 видно, что при таких условиях
спектральное число ее обусловленности
(см. рис. 1, справа). Из рис. 1 видно, что при таких условиях
спектральное число ее обусловленности ![]() матрицы
матрицы
![]() достигает значений порядка 104.
Для других видов матриц
достигает значений порядка 104.
Для других видов матриц ![]() при прочих равных условиях число обусловленности
может быть еще выше и достигать величины 1017.
при прочих равных условиях число обусловленности
может быть еще выше и достигать величины 1017.
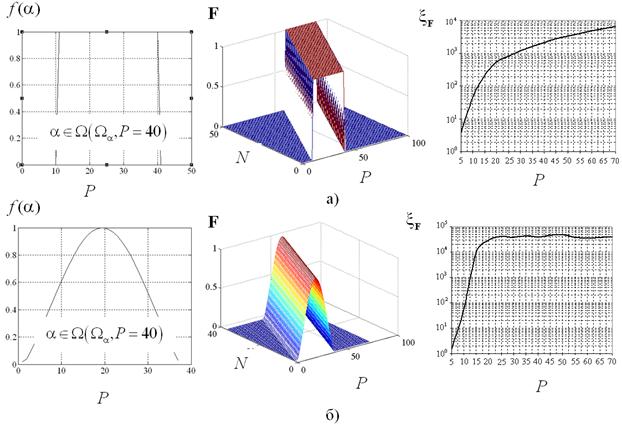
Рис. 1. Сеточные аналоги ядер интегрального уравнения (1)
вида ![]() (а),
главного лепестка
(а),
главного лепестка ![]() (б),
(б),
![]() (слева), матрицы коэффициентов
(слева), матрицы коэффициентов ![]() СЛАУ (4) (в центре)
СЛАУ (4) (в центре)
и их спектральные числа обусловленности ![]() (справа)
(справа)
Число
обусловленности ![]() матрицы коэффициентов
матрицы коэффициентов ![]() СЛАУ (4) весьма важно, т. к.
определяет чувствительность ошибок в решении в зависимости от возмущений:
вектора наблюдения
СЛАУ (4) весьма важно, т. к.
определяет чувствительность ошибок в решении в зависимости от возмущений:
вектора наблюдения ![]() , матрицы коэффициентов СЛАУ
, матрицы коэффициентов СЛАУ ![]() и обратной к ней матрицы
и обратной к ней матрицы ![]() , одновременно вектора наблюдения
, одновременно вектора наблюдения ![]() и матрицы коэффициентов
и матрицы коэффициентов ![]() СЛАУ (4).
СЛАУ (4).
Причина
плохой обусловленности заключается в том, что при ![]() столбцы
матрицы коэффициентов
столбцы
матрицы коэффициентов ![]() становятся линейно зависимыми
(коррелированными). Известно, что при разрешении сигналов основным требованием
к оператору преобразования
становятся линейно зависимыми
(коррелированными). Известно, что при разрешении сигналов основным требованием
к оператору преобразования ![]() является обеспечение
линейной независимости его столбцов. Связано это с тем, что линейно зависимые
системы не несут дополнительной информации и не могут быть использованы для
повышения информативности. При этом с помощью такого оператора преобразования
является обеспечение
линейной независимости его столбцов. Связано это с тем, что линейно зависимые
системы не несут дополнительной информации и не могут быть использованы для
повышения информативности. При этом с помощью такого оператора преобразования ![]() становится невозможным обеспечить высокое
разрешение сигналов.
становится невозможным обеспечить высокое
разрешение сигналов.
Таким
образом, для поставленной задачи разрешения в виде СЛАУ (4) не выполнено третье
условие корректности задачи, а именно условие устойчивости. Поэтому сформулированная
задача разрешения является некорректно поставленной. Наличие шумов наблюдения ![]() во входной выборке
во входной выборке ![]() приводит к несовместности системы
уравнений (4), т. к. в число неизвестных входит еще и случайная величина,
определяемая шумами наблюдения. Получить строгое решение такой системы
уравнений невозможно принципиально и приходится выбирать то или иное
квазирешение системы уравнений (4), обеспечивающее его единственность и устойчивость.
приводит к несовместности системы
уравнений (4), т. к. в число неизвестных входит еще и случайная величина,
определяемая шумами наблюдения. Получить строгое решение такой системы
уравнений невозможно принципиально и приходится выбирать то или иное
квазирешение системы уравнений (4), обеспечивающее его единственность и устойчивость.
Рассмотрим
один из возможных подходов к разрешению сигналов на основе линейных
преобразований, описываемых ортогональными (унитарными) матрицами. Критериями
для выбора метода получения квазирешения СЛАУ могут служить закономерности
изменения числа обусловленности ![]() матрицы коэффициентов линейного оператора
матрицы коэффициентов линейного оператора ![]() ,
точность ее представления, объем вычислительной
процедуры и характер поведения невязки. Допущениями,
используемыми при обосновании предлагаемого ниже метода разрешения, являются
следующие: известен оператор
,
точность ее представления, объем вычислительной
процедуры и характер поведения невязки. Допущениями,
используемыми при обосновании предлагаемого ниже метода разрешения, являются
следующие: известен оператор ![]() преобразования
(аппаратная функция системы), известны
величина
относительного возмущения
преобразования
(аппаратная функция системы), известны
величина
относительного возмущения ![]() матрицы оператора
преобразования
матрицы оператора
преобразования ![]() и вероятностные характеристики
шумов наблюдения.
и вероятностные характеристики
шумов наблюдения.
В
разработанный метод заложено ряд принципов. Первый принцип – формирование
такой матрицы оператора преобразования входного наблюдения, функционально связанного
с матрицей исходного ![]() линейного
оператора, которая обеспечивает линейную независимость сигналов на выходе. Этот
принцип следует из анализа постановки задачи разрешения, где показано, что матрица
оператора преобразования
линейного
оператора, которая обеспечивает линейную независимость сигналов на выходе. Этот
принцип следует из анализа постановки задачи разрешения, где показано, что матрица
оператора преобразования ![]() в
ее исходном виде не может быть использована для повышения разрешающей
способности в силу плохой обусловленности. Второй
принцип – количество линейно независимых
(ортогональных, унитарных) каналов
в
ее исходном виде не может быть использована для повышения разрешающей
способности в силу плохой обусловленности. Второй
принцип – количество линейно независимых
(ортогональных, унитарных) каналов ![]() , сформированных из
матрицы оператора
, сформированных из
матрицы оператора ![]() должно быть не менее числа
разрешаемых сигналов
должно быть не менее числа
разрешаемых сигналов ![]() . Третий принцип
является следствием первого – при разрешении сигналов исключить преобразования
входного наблюдения, приводящие к формированию линейной зависимости и ухудшению
обусловленности системы уравнений. Первый–третий принципы предлагаемого метода
разрешения могут быть реализованы с использованием ортогональных (унитарных)
линейных преобразований. Четвертый принцип – минимум априорной информации
о модели функции
. Третий принцип
является следствием первого – при разрешении сигналов исключить преобразования
входного наблюдения, приводящие к формированию линейной зависимости и ухудшению
обусловленности системы уравнений. Первый–третий принципы предлагаемого метода
разрешения могут быть реализованы с использованием ортогональных (унитарных)
линейных преобразований. Четвертый принцип – минимум априорной информации
о модели функции ![]() . Этот
принцип соответствует тому, что на практике информация о функции
. Этот
принцип соответствует тому, что на практике информация о функции ![]() либо неизвестна, либо носит
неопределенный характер. Пятый принцип – извлечение максимума информации
из известного оператора преобразования
либо неизвестна, либо носит
неопределенный характер. Пятый принцип – извлечение максимума информации
из известного оператора преобразования ![]() . Под этим понимается величина
матричной нормы
. Под этим понимается величина
матричной нормы ![]() , величина относительного
возмущения
, величина относительного
возмущения ![]() и число обусловленности
и число обусловленности ![]() матрицы коэффициентов
оператора преобразования
матрицы коэффициентов
оператора преобразования ![]() .
Число обусловленности
.
Число обусловленности ![]() характеризует
степень неустойчивости решения. На устойчивость
решения СЛАУ (4) влияют три основных фактора – возмущение вектора наблюдения
под воздействием шума, точность представления
матрицы коэффициентов СЛАУ и ее обусловленность.
Причем число обусловленности матрицы коэффициентов СЛАУ является универсальной
характеристикой. Оно связывает между собой все вышеназванные и весьма важные
для разрешения сигналов факторы. Кроме того, число обусловленности существует
для матриц произвольной размерности и используется для классификации степени
некорректности обратных задач. Задача разрешения как раз к таким и относится. Это
позволяет предложить число обусловленности
характеризует
степень неустойчивости решения. На устойчивость
решения СЛАУ (4) влияют три основных фактора – возмущение вектора наблюдения
под воздействием шума, точность представления
матрицы коэффициентов СЛАУ и ее обусловленность.
Причем число обусловленности матрицы коэффициентов СЛАУ является универсальной
характеристикой. Оно связывает между собой все вышеназванные и весьма важные
для разрешения сигналов факторы. Кроме того, число обусловленности существует
для матриц произвольной размерности и используется для классификации степени
некорректности обратных задач. Задача разрешения как раз к таким и относится. Это
позволяет предложить число обусловленности ![]() матриц
линейных операторов систем уравнений вида (4) и др., предназначенных для
поиска квазирешений при разрешении сигналов, в качестве потенциальной характеристики
устойчивости того или иного метода сверхразрешения. В качестве асимптотических
характеристик устойчивости решения СЛАУ при разрешении сигналов целесообразно
использовать также математическое ожидание и корреляционную матрицу вектора
решений СЛАУ. Наряду с числом обусловленности
матриц
линейных операторов систем уравнений вида (4) и др., предназначенных для
поиска квазирешений при разрешении сигналов, в качестве потенциальной характеристики
устойчивости того или иного метода сверхразрешения. В качестве асимптотических
характеристик устойчивости решения СЛАУ при разрешении сигналов целесообразно
использовать также математическое ожидание и корреляционную матрицу вектора
решений СЛАУ. Наряду с числом обусловленности ![]() необходимо использовать также
еще один показатель обусловленности – это скорость убывания сингулярных чисел
необходимо использовать также
еще один показатель обусловленности – это скорость убывания сингулярных чисел ![]() матрицы
матрицы ![]() . Показатель
. Показатель ![]() характеризует форму ядра
характеризует форму ядра ![]() интегрального
уравнения (1). Установлено, что скорость
убывания сингулярных чисел
интегрального
уравнения (1). Установлено, что скорость
убывания сингулярных чисел ![]() минимальна для тех матриц оператора преобразования
минимальна для тех матриц оператора преобразования ![]() , у которых максимальна величина
матричной нормы
, у которых максимальна величина
матричной нормы ![]() , т. е. для оператора
, т. е. для оператора ![]() с прямоугольной огибающей.
Как правило, эта информация доступна на этапе разработки алгоритма разрешения в
той или иной конкретной радиолокационной системе. Шестой принцип – задача
разрешения сигналов должна ставиться тогда, когда энергетические соотношения
между сигналами и шумами наблюдения позволяют обеспечить заданные показатели
качества разрешения. Шестой
принцип говорит о следующем. Чтобы обеспечить требуемые с заданными показателями
качества характеристики разрешения сигналов необходимо вполне определенное отношение
сигнал-шум во входных данных. Такие оценки можно получить аналитически и с
помощью моделирования
для конкретной радиолокационной системы.
с прямоугольной огибающей.
Как правило, эта информация доступна на этапе разработки алгоритма разрешения в
той или иной конкретной радиолокационной системе. Шестой принцип – задача
разрешения сигналов должна ставиться тогда, когда энергетические соотношения
между сигналами и шумами наблюдения позволяют обеспечить заданные показатели
качества разрешения. Шестой
принцип говорит о следующем. Чтобы обеспечить требуемые с заданными показателями
качества характеристики разрешения сигналов необходимо вполне определенное отношение
сигнал-шум во входных данных. Такие оценки можно получить аналитически и с
помощью моделирования
для конкретной радиолокационной системы.
В предлагаемом методе разрешения, устойчивость решения обеспечивается за счет исключения из пространства решений тех направлений, в которых отношение сигнала к шуму не превышает некоторого порогового значения по причине малых значений соответствующих сингулярных чисел матрицы оператора преобразования системы, а также отсутствия составляющих эхосигнала цели в указанных направлениях.
Практическая реализация предлагаемого метода включает два этапа. Первый этап предварительный. Он реализуется при проектировании РЛС и формировании ее программного обеспечения. Второй этап (собственно разрешения сигналов) реализуется непосредственно в ходе функционирования РЛС. Рассмотрим сущность каждого из этапов.
Первый
этап. Для заданного ![]() находят его конечномерную аппроксимацию
находят его конечномерную аппроксимацию
![]() , где
, где ![]() –
– ![]() -матрица
оператора преобразования системы. Основное требование определено вторым
принципом
-матрица
оператора преобразования системы. Основное требование определено вторым
принципом ![]() . Связано оно с тем, что количество
линейно независимых (ортогональных, унитарных) каналов
. Связано оно с тем, что количество
линейно независимых (ортогональных, унитарных) каналов ![]() ,
сформированных из матрицы
,
сформированных из матрицы ![]() оператора
оператора ![]() должно
быть не менее числа разрешаемых сигналов
должно
быть не менее числа разрешаемых сигналов ![]() .
В любом случае все методы разрешения в той или иной форме используют
ограничение сверху на максимальное число разрешаемых сигналов, т. е.
следуют сформулированному принципу. Далее строится сингулярное разложение
матрицы
.
В любом случае все методы разрешения в той или иной форме используют
ограничение сверху на максимальное число разрешаемых сигналов, т. е.
следуют сформулированному принципу. Далее строится сингулярное разложение
матрицы ![]() :
:
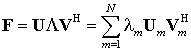 ,
,
где ![]() – унитарная матрица порядка N;
– унитарная матрица порядка N; ![]() –
диагональная N×P-матрица сингулярных значений
–
диагональная N×P-матрица сингулярных значений ![]() матрицы оператора преобразования
матрицы оператора преобразования ![]() ;
; ![]() – унитарная матрица порядка P.
– унитарная матрица порядка P.
Выбирается
число ![]() исходя, например, из точности
представления матрицы линейного оператора
исходя, например, из точности
представления матрицы линейного оператора ![]() .
Например, из условия
.
Например, из условия ![]()
![]() , где
, где ![]() – относительные возмущения
матрицы коэффициентов системы
– относительные возмущения
матрицы коэффициентов системы ![]() . Нет смысла
искать решение точнее, чем представлена матрица оператора преобразования
системы
. Нет смысла
искать решение точнее, чем представлена матрица оператора преобразования
системы ![]() .
Могут быть и другие условия определения
.
Могут быть и другие условия определения ![]() ,
связанные, например, с числом обусловленности
,
связанные, например, с числом обусловленности ![]() матрицы
матрицы
![]() или предполагаемым уровнем шумов наблюдения.
или предполагаемым уровнем шумов наблюдения.
На
основании теорем о сингулярном разложении и понятии псевдообратной матрицы Мура – Пенроуза
[12] получаем сначала матрицу ![]() , а затем и
диагональную
N×P-матрицу
, а затем и
диагональную
N×P-матрицу ![]() сингулярных значений оператора
преобразования
сингулярных значений оператора
преобразования
![]() , которые определяются однозначно. Для матрицы
, которые определяются однозначно. Для матрицы
![]()
псевдообратной является матрица
![]() .
.
Первый этап
заканчивается сохранением рассчитанных матриц ![]() ,
, ![]() ,
, ![]() в запоминающее устройство
бортового вычислителя РЛС на этапе формирования ее программного обеспечения.
Ясно, что этот этап не требует больших вычислительных и временных затрат.
в запоминающее устройство
бортового вычислителя РЛС на этапе формирования ее программного обеспечения.
Ясно, что этот этап не требует больших вычислительных и временных затрат.
Второй
этап. Ищется псевдорешение СЛАУ (4).
Псевдорешение предлагается искать среди решений СЛАУ вида ![]() , откуда с учетом теорем
о сингулярном разложении и псевдообращении матриц получим
, откуда с учетом теорем
о сингулярном разложении и псевдообращении матриц получим
![]() .
(5)
.
(5)
В ходе функционирования РЛС для тех элементов разрешения, в которых принято решение об обнаружении групповой цели, реализуется операция векторно-матричного умножения (5) и сравнение полученной величины с порогом
![]() , (6)
, (6)
где
k –
коэффициент, определяющий условную вероятность ложных тревог ![]() при разрешении сигналов;
при разрешении сигналов; ![]() – порог разрешения. Элементы вектора
– порог разрешения. Элементы вектора ![]() , которые
удовлетворяют условию (6), считаются оценкой
, которые
удовлетворяют условию (6), считаются оценкой ![]() модели наблюдения неизвестного эхосигнала, сформированного
объектом локации, т. е. решением СЛАУ (4). Последнее также можно
трактовать как физически обоснованное требование учета тех сигналов, амплитуда
которых превышает в заданное число раз среднеквадратичное значение шума. Количество этих элементов определяет оценку числа
эхосигналов
модели наблюдения неизвестного эхосигнала, сформированного
объектом локации, т. е. решением СЛАУ (4). Последнее также можно
трактовать как физически обоснованное требование учета тех сигналов, амплитуда
которых превышает в заданное число раз среднеквадратичное значение шума. Количество этих элементов определяет оценку числа
эхосигналов ![]() , сформировавших
, сформировавших ![]() , а их положение
– оценку вектора параметров
, а их положение
– оценку вектора параметров ![]() сигналов.
сигналов.
Найдем
математическое ожидание ![]() оценки (5). Относительно вектора наблюдения
оценки (5). Относительно вектора наблюдения
![]() полагаем, что он возмущен случайным
вектор-столбцом
полагаем, что он возмущен случайным
вектор-столбцом ![]() размерностью
размерностью ![]() . Математическое ожидание вектор-столбца
. Математическое ожидание вектор-столбца ![]() считается равным нулю:
считается равным нулю: ![]() , а его корреляционная матрица равна
, а его корреляционная матрица равна ![]() , где
, где ![]() -
- ![]() -единичная
матрица,
-единичная
матрица, ![]() - мощность шума. Тогда:
- мощность шума. Тогда:
![]() . (7)
. (7)
При получении (7) учтено,
что в силу унитарности ![]() и
и ![]() . Выражение
(7) свидетельствует о том, что формируемые оценки являются
асимптотически состоятельными. Найдем корреляционную матрицу
. Выражение
(7) свидетельствует о том, что формируемые оценки являются
асимптотически состоятельными. Найдем корреляционную матрицу ![]() оценки (5). Для этого предварительно покажем,
что
оценки (5). Для этого предварительно покажем,
что
![]() .
.
Тогда с учетом (7), для
корреляционной матрицы ![]() получим:
получим:
![]()
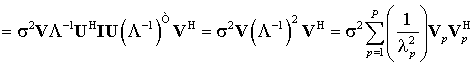 . (8)
. (8)
Выражение (8) является мощным инструментом как для оценки влияния
различных факторов на потенциальные возможности метода, так и для вычисления
порогов для выражения (6). Фактически оно позволяет ответить на вопрос о той «плате»,
которую необходимо заплатить за сверхразрешение сигналов. Анализ формулы (8)
показывает, что разрешение существенно зависит как от отношения сигнал-шум, вида
и точности представления оператора преобразования, так и метода обработки сигналов.
В частности видно, что дисперсия оценок является взвешенной линейной комбинацией
![]() собственных векторов матрицы линейного
оператора
собственных векторов матрицы линейного
оператора ![]() . В качестве весов выступают величины
. В качестве весов выступают величины ![]() обратные квадратам сингулярных значений
обратные квадратам сингулярных значений ![]() . Поэтому большое значение имеет скорость убывания
сингулярных чисел
. Поэтому большое значение имеет скорость убывания
сингулярных чисел ![]() с ростом числа
разрешаемых сигналов
с ростом числа
разрешаемых сигналов ![]() , а также характер изменения
, а также характер изменения ![]() при различного рода преобразованиях
при различного рода преобразованиях ![]() . Кроме того, из (8) следует, что повышение разрешающей способности
(увеличение
. Кроме того, из (8) следует, что повышение разрешающей способности
(увеличение ![]() ) требует увеличения отношения сигнал-шум и точности представления
матрицы линейного оператора
) требует увеличения отношения сигнал-шум и точности представления
матрицы линейного оператора ![]() ,
т. к. с ростом
,
т. к. с ростом ![]() сингулярные
числа
сингулярные
числа ![]() быстро уменьшаются, дисперсия
увеличивается как
быстро уменьшаются, дисперсия
увеличивается как ![]() , а относительные возмущения
, а относительные возмущения ![]() матрицы линейного
оператора
матрицы линейного
оператора ![]() ограничены условием
ограничены условием ![]() .
.
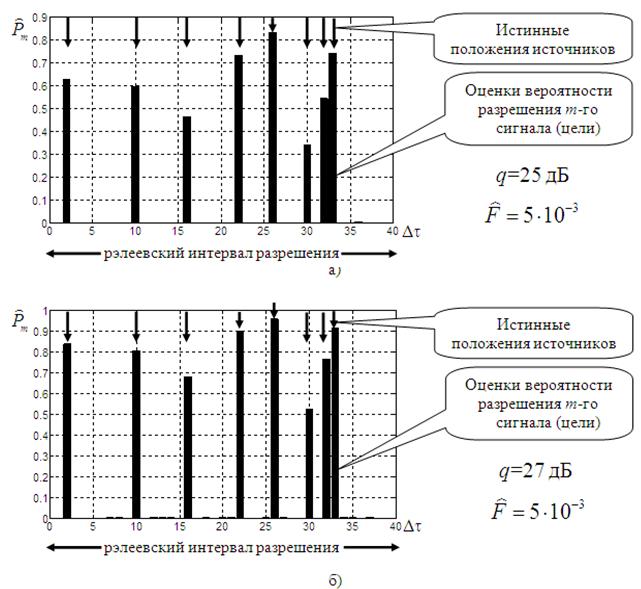
Рис. 2. Оценки вероятности ![]() разрешения m-го сигнала (цели).
разрешения m-го сигнала (цели).
Детерминированные амплитуды сигналов (целей):
а – отношение сигнал-шум q=25 дБ;
б – отношение сигнал-шум q=27 дБ
Проверка адекватности полученных закономерностей, а также оценка эффективности предлагаемого метода разрешения проводились с помощью имитационного моделирования. Моделировался групповой РЛО, состоящий из восьми отдельных целей, находящихся на фиксированных взаимных удалениях от 0,025 до 0,2 рэлеевского интервала разрешения по времени запаздывания (дальности). Отдельные результаты моделирования приведены на рисунках 2−4.
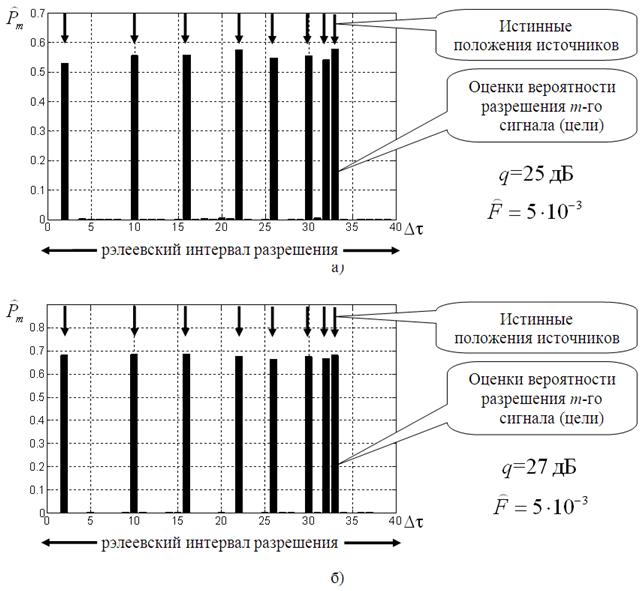
Рис. 3. Оценки вероятности ![]() разрешения m-го сигнала (цели).
разрешения m-го сигнала (цели).
Случайные амплитуды сигналов (целей):
а – среднее отношение сигнал-шум q=25 дБ;
б – среднее отношение сигнал-шум q=27 дБ
На рис. 2, 3
по оси
абсцисс отложены
относительные дискретные отсчеты ![]() по времени
запаздывания (дальности) в пределах рэлеевского интервала разрешения. Стрелками
показаны истинные положения сигналов. По оси ординат показаны оценки
вероятности
по времени
запаздывания (дальности) в пределах рэлеевского интервала разрешения. Стрелками
показаны истинные положения сигналов. По оси ординат показаны оценки
вероятности ![]() разрешения
m-го сигнала (цели) из состава группового РЛО в зависимости от отношения
сигнал-шум q для случая детерминированных (см.
рис. 2) и случайных (см. рис. 3) амплитуд сигналов, флюктуирующих
независимо друг от друга по рэлеевскому закону. Фазы
сигналов всегда полагались случайными и распределенными по равномерному закону
в диапазоне значений 0–2π. Оценки вероятностей
разрешения
m-го сигнала (цели) из состава группового РЛО в зависимости от отношения
сигнал-шум q для случая детерминированных (см.
рис. 2) и случайных (см. рис. 3) амплитуд сигналов, флюктуирующих
независимо друг от друга по рэлеевскому закону. Фазы
сигналов всегда полагались случайными и распределенными по равномерному закону
в диапазоне значений 0–2π. Оценки вероятностей ![]() получены по результатам
1000 независимых реализаций, что обеспечивало точность статистического эксперимента порядка
3–5 %. Порог устанавливался по аналогии с
критерием Неймана-Пирсона. При этом априори задавалась вероятность ложных тревог
получены по результатам
1000 независимых реализаций, что обеспечивало точность статистического эксперимента порядка
3–5 %. Порог устанавливался по аналогии с
критерием Неймана-Пирсона. При этом априори задавалась вероятность ложных тревог
![]() . Это значит,
что в отсутствии эхосигнала вероятность превышения хотя бы одним элементом
вектора
. Это значит,
что в отсутствии эхосигнала вероятность превышения хотя бы одним элементом
вектора ![]() порогового
значения
порогового
значения ![]() не
превышала
не
превышала ![]() . При моделировании оценка
вероятности ложной тревоги
. При моделировании оценка
вероятности ложной тревоги ![]() составляла
величину равную 5·10–3.
составляла
величину равную 5·10–3.
Отдельные результаты моделирования по разрешению сложной групповой цели приведены на рис. 4. Моделировалась цель, состоящая из двух плотных групп, по пять отдельных целей в каждой, находящихся на взаимном удалении от 0,05 до 0,15 рэлеевского интервала разрешения по времени запаздывания (дальности). Причем в составе каждой группы присутствовал один мощный источник сигнала, существенно превосходящий по амплитуде остальные. Амплитуды остальных сигналов отдельных целей полагались приблизительно равными, фазы случайными. Истинное взаимное расположение сигналов по времени запаздывания (дальности) и их относительную интенсивность хорошо видно на рис. 4д при высоком отношении сигнал-шум (более 100 дБ). На рис. 4а,в видна получающаяся при этом сигнальная смесь, которая подлежит разрешению.
Разрешение выполнялось при отношении сигнал-шум около 27 дБ (см. рис. 2б, г, е). Результат разрешения сигналов по времени запаздывания (дальности) представлен на рисунке 4е. На нем показаны оценки восстановленных амплитуд сигналов, максимумы которых соответствуют оценкам времен запаздывания (дальностей) каждого из источников сигналов (отдельных целей).
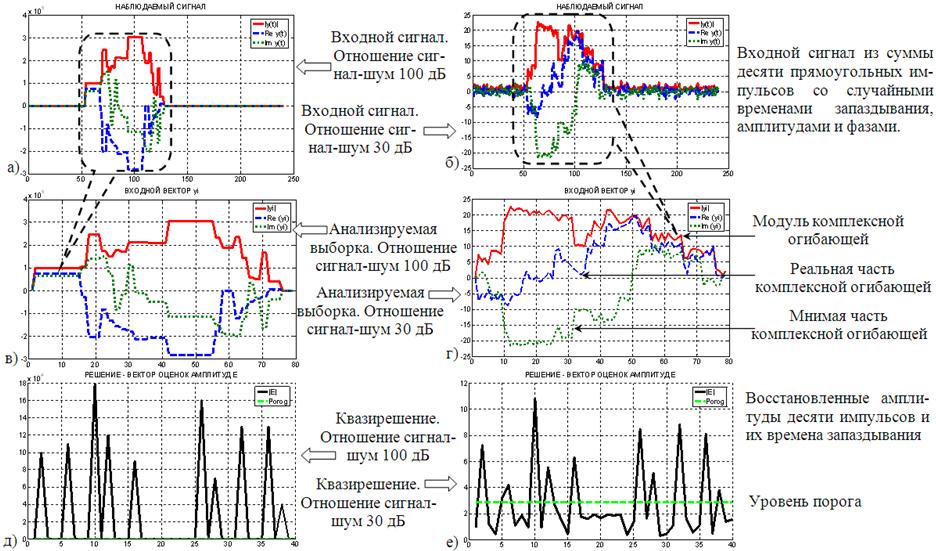
Рис. 4. Результаты имитационного моделирования разрешения десяти перекрывающихся по времени сигналов
Анализ
результатов моделирования позволяет заключить, что эффективность предложенного
метода сверхразрешения достаточно высока. Например, из рисунка следует, что при
отношении сигнал-шум в 27 дБ с вероятностью ![]() возможно
обеспечить 2,5 % интервал разрешения случайных сигналов по отношению к
рэлеевскому интервалу. Метод прост в технической реализации и обеспечивает
получение устойчивого разрешения группового РЛО с использованием узкополосного
зондирующего сигнала в реальном масштабе времени. Практическую ценность при реализации предлагаемого
метода повышения разрешающей способности представляют новые функциональные
возможности РЛС, обусловленные высокими характеристиками по разрешению целей, образующих в их импульсном объеме плотные группы
из четырех – десяти целей.
возможно
обеспечить 2,5 % интервал разрешения случайных сигналов по отношению к
рэлеевскому интервалу. Метод прост в технической реализации и обеспечивает
получение устойчивого разрешения группового РЛО с использованием узкополосного
зондирующего сигнала в реальном масштабе времени. Практическую ценность при реализации предлагаемого
метода повышения разрешающей способности представляют новые функциональные
возможности РЛС, обусловленные высокими характеристиками по разрешению целей, образующих в их импульсном объеме плотные группы
из четырех – десяти целей.
Заключение
С точки зрения разрешения неортогональных сигналов исходная СЛАУ (4), которая имеется до проведения с ней каких-либо линейных преобразований, обладает наилучшими потенциальными характеристиками по разрешению сигналов. Любое линейное преобразование СЛАУ (4) с матрицей, у которой обусловленность отличается от единицы, может только ухудшить эти характеристики. Исключение составляют линейные преобразования, описываемые ортогональными (унитарными) матрицами, что реализовано в предложенном методе сверхразрешения сигналов с использованием указанных линейных преобразований.
При эквивалентных показателях устойчивости с известными методами наименьших квадратов и максимального правдоподобия, предложенный метод разрешения, с использованием сингулярного разложения, существенно проще в вычислительном отношении и может быть реализован в процессе функционирования РЛС в реальном масштабе времени.
Практическую ценность при реализации предлагаемого метода повышения разрешающей способности представляют новые функциональные возможности РЛС, обусловленные высокими характеристиками по разрешению целей, образующих в их импульсном объеме плотные группы из четырех – десяти целей. Последнее подтверждается результатами имитационного математического моделирования.
1. Радиоэлектронные системы: Основы построения и теория. Справочник. Изд. 2-е./ Под ред. Я. Д. Ширмана. М., Радиотехника, 2007. 512 с.
2. Стрэтт Д. В. Волновая теория света. М., Государственное издательство технико-теоретической литературы, 1940.
3. Вудворд Ф. М. Теория вероятностей и теория информации с применениями в радиолокации. Сов. радио, М., 1955.
4. Хелстром К. Статистическая теория обнаружения сигналов. М., Изд-во иностр. лит., 1963. 432 с.
5. Ширман Я. Д. Разрешение и сжатие сигналов. М., Сов. радио, 1974. 315 с.
6. Трифонов А. П., Шинаков Ю. С. Совместное различение сигналов и оценка их параметров на фоне помех. М., Радио и связь, 1986. 264 с.
7. Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения / Пер. с англ. М., Мир, 1990.
8. Чижов А. А. Сверхрэлеевское разрешение. Т. 2. Преодоление фактора некорректности обратной задачи рассеяния и проекционная радиолокация. М., Красанд, 2010. 104 с.
9. Косарев Е. Л. Методы обработки экспериментальных данных. 2-е изд., М., Физматлит, 2008. 208 с.
10. Арсенин В. Я. Методы математической физики и специальные функции. М., Наука, 1974. 433 с.
11. Воеводин В. В., Воеводин Вл. В. Энциклопедия линейной алгебры. СПб, БХВ-Петербург, 2006. 544 с.
12. Хорн Р., Джонсон Ч. Матричный анализ. М., Мир, 1990. 655 с.