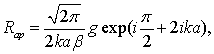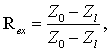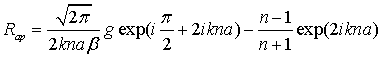Исследование сверхширокополосной кольцевой антенной решетки

В. Л. Бирюков, Н. А. Ефимова, В. И. Калиничев, В. А. Калошин, Л. И. Пангонис

ИРЭ им. В.А. Котельникова РАН

Получена 15 января 2013 г.

Аннотация: Рассмотрена задача синтеза и анализа кольцевой антенной решетки для азимутального сканирования в сверхширокой полосе частот (более 1:100). Дан обзор СШП излучателей, используемых в качестве элементов антенных решеток. Приведены результаты анализа характеристик согласования различных модификаций ТЕМ рупоров с использованием численно-аналитической теории и методом конечных элементов. Проведено численное моделирование характеристик согласования и излучения кольцевой антенной решетки с использованием несимметричного петлевого ТЕМ рупора в качестве элемента. Проведено сопоставление результатов численного моделирования и физического эксперимента.

Ключевые слова: сверхширокополосные антенны, ТЕМ рупоры, кольцевые антенные решетки.

Abstract: The problem of synthesis and analysis of circular antenna array for the azimuth scanning in ultra-wide band (more than 1:100) is considered. The review of UWB radiators used as the elements of antenna arrays is given. The results of the matching characteristics analysis of various modifications of TEM horns have been obtained with the use of a numerical-analytical theory and FEM are given. Numerical modeling of the matching characteristics of and radiation of a circular antenna array of asymmetrical loop TEM horns as elements is done. Comparison of the results of numerical simulation and physical experiment is conducted.

Keywords: ultra wideband antenna, TEM horn, circular antenna array.

 

Введение

Сверхширокополосные (СШП) антенные решетки широко используются в качестве антенн в системах СШП радиолокации и связи. К настоящему времени по этой тематике опубликовано большое количество работ (см., например, [1-10]). В качестве элементов антенных решеток в данных исследованиях используются самые различные разновидности СШП антенн: логопериодические, неоднородные щелевые (антенны Вивальди), биконические, пирамидальные и нерегулярные ТЕМ рупоры.

Одними из наиболее популярных видов СШП антенн, использующихся в качестве элементов кольцевых антенных решеток являются биконические ТЕМ рупоры. Эти антенны легко согласуются с 50-омной линией, но в составе решетки сильно взаимодействуют с соседними элементами из-за всенаправленной в азимутальной плоскости диаграммы направленности. ТЕМ рупоры обладают хорошей направленностью, а их согласование и характеристики излучения достаточно слабо зависят от взаимодействия с соседними элементами. Ширина диаграммы направленности ТЕМ рупора в Н-плоскости стабильна в полосе частот и сравнима с угловым размером излучателя в этой плоскости (кроме самых нижних частот). Благодаря этому, а также форме, которая позволяет естественным образом вписаться в сектор расположения элемента решетки, TEM рупор является хорошим кандидатом для использования в качестве СШП излучателя для кольцевой антенной решетки.

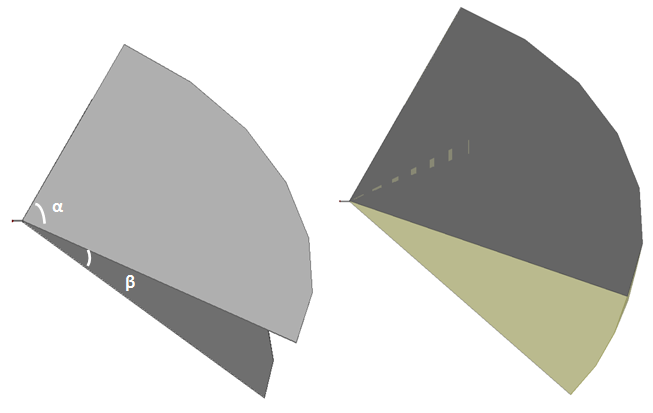
Основными геометрическими параметрами ТЕМ рупора (рис. 1) являются его длина и два угла: α, определяющий угловой размер пластин и β − угол между пластинами. Следует отметить, что традиционным недостатком рупорных антенн является относительно большая электрическая длина и большая разница в углах α и β.

 

Рис. 1. Классический ТЕМ рупор	Рис. 2. Металло-диэлектрический TEM рупор

В работе [11] была предложена и исследована металлодиэлектрическая рупорно-линзовая антенна (МДРЛА), которая характеризуется уменьшенной длиной и увеличенным коэффициентом усиления. Еще большее уменьшение продольного размера СШП элемента может быть получено с использованием нерегулярных ТЕМ рупоров: симметричного (рис. 3) и петлевого несимметричного (рис. 4).

 

 

В первом разделе данной работе построена численно-аналитическая теория согласования регулярных ТЕМ рупоров, в том числе с диэлектрическим заполнением, исследование этих рупоров проведено во втором разделе, в третьем разделе исследовано согласование нерегулярных ТЕМ рупоров, в четвертом разделе проведено теоретическое и экспериментальное исследование семиэлементной кольцевой антенной решетки из несимметричных петлевых ТЕМ рупоров.

 

1.                Численно-аналитическая теория согласования ТЕМ рупоров

Коэффициент отражения рупора представим в виде суммы двух компонент: первая из них описывает отражение от апертуры рупора, а вторая – от узла возбуждения. Первая компонента находится на основе асимптотического разложения коэффициента отражения от апертуры двухмерного рупора, полученного в [12], выражение для первого члена которого может быть представлено в следующем виде:

(1)

 

где β – соответствующий угол (в радианах), a – длина рупора, k – волновое число в свободном пространстве, g – дифракционный коэффициент.

Для получения второй компоненты коэффициента отражения используем теорию длинных линий, в соответствии с которой коэффициент отражения от узла возбуждения может быть представлен в виде:

(2)

 

где Z₀ – волновое сопротивление питающей линии, а Z_l – ТЕМ рупора. Для связи геометрических параметров рупора (углов α и β) и величины его волнового сопротивления будем использовать приближение, полученное в работе [13].

Для рупора, заполненного диэлектриком (рис. 2), k в формуле (1) заменяется на kn и добавляется еще один член, описывающий отражение от диэлектрика. В результате для коэффициента отражения от апертуры получаем:

(3)

 

2.                Исследование согласования регулярных TEM рупоров

Первый из исследованных с помощью полученных формул рупоров – ТЕМ рупор с апертурой, обрезанной по сфере c радиусом, равным длине рупора , с параметрами: α = 90º, β = 20.7 (соответствует сопротивлению 50 Ом согласно работе [13]) и a = 500mm. На рис. 5 приведена зависимость коэффициента отражения от частоты, рассчитанная по формулам (1), (2) с g = -1 (пунктирная линия) и g = -0.77 (штриховая линия). Уменьшенное значение дифракционного коэффициента учитывает, что часть мощности излучается через боковые щели ТЕМ рупора. Сплошной линией приведена аналогичная зависимость, рассчитанная методом конечных элементов. Как видно на рис. 5, формула (1) с g = -0.77 лучше описывает коэффициент отражения рупора.

На рис. 6 приведены аналогичные зависимости для металло-диэлектрического ТЕМ рупора (МДТР), заполненного диэлектриком с ε = 2.25 и обрезанного по сфере, радиусом равной длине рупора, с параметрами: α = 90º, β = 37.34º (соответствует сопротивлению 75 Ом согласно работе [13]), a = 500mm. Как видно из рис. 6 численно-аналитическая теория описывает согласование МДТР немного хуже, чем классического ТЕМ рупора. Отметим, что в случае МДТР коэффициент отражения на нижних частотах несколько лучше описывает формула с использованием g = -1. Это объясняется тем, что в этом случае мощностью, излучаемой через боковые щели, с учетом эффекта полного внутреннего отражения от границы диэлектрика можно пренебречь.

 

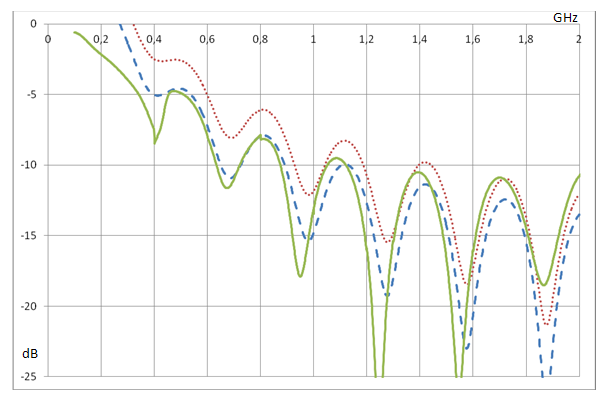
Рис. 5. Зависимость коэффициента отражения классического ТЕМ рупора от частоты.

 

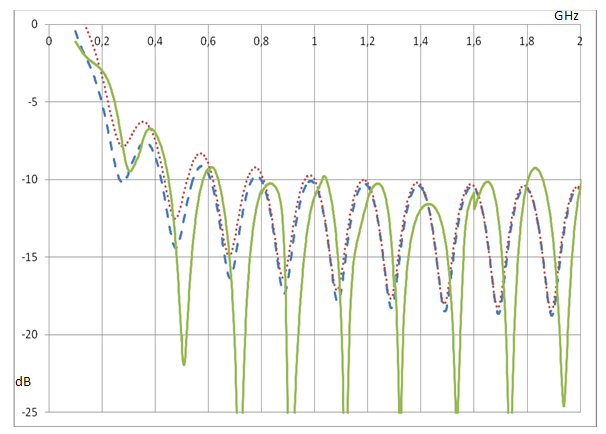
Рис. 6. Зависимость коэффициента отражения рупора, заполненного диэлектриком, от частоты

 

3.                Исследование согласования нерегулярных TEM рупоров

Первым из нерегулярных рупоров исследовался экспоненциальный рупор (рис. 3), образующая которого описывается формулой: , где h(x) – изменение расстояния между пластинами рупора в зависимости от расстояния от узла возбуждения, h0 – расстояние между пластинами рупора в узле возбуждения, a и b – параметры. Коэффициент отражения рупора вычислялся с помощью численной процедуры на основе метода конечных элементов, а параметры оптимизировались с использованием генетического алгоритма. Результаты моделирования для оптимальных значений параметров (a =  50mm, b = 14.85) приведены на рис. 7.

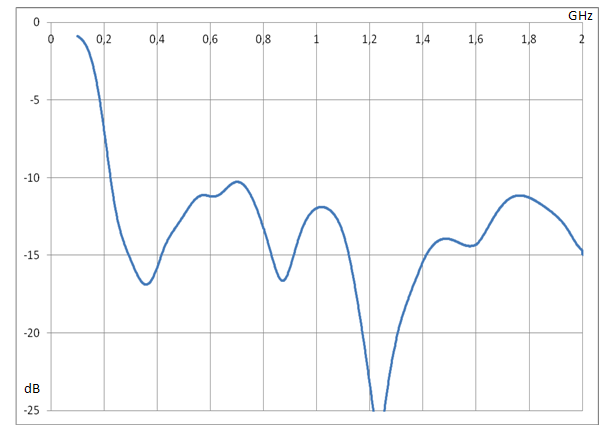
Рис. 7. Зависимость коэффициента отражения экспоненциального рупора от частоты

 

В работе также исследован новый тип СШП излучателей – несимметричный петлевой ТЕМ рупор (рис. 4). Конструкция несимметричного петлевого ТЕМ рупора отличается не только использованием замкнутой формы одной из его стенок, но и модификацией узла возбуждения (рис. 8). Одна из стенок этого излучателя образует петлю, два конца которой подключены к внутреннему и внешнему проводникам 50-омного коаксиального кабеля. Другая стенка ТЕМ рупора образована плоским экраном, который соединен с внешним проводником коаксиального кабеля, как показано на рис. 8.

 

Рис. 8. Схема возбуждения несимметричного петлевого ТЕМ рупора

 

Были проведены исследования зависимости согласования несимметричного петлевого TEM рупора от формы экрана, подключенного и образующей петли.

 

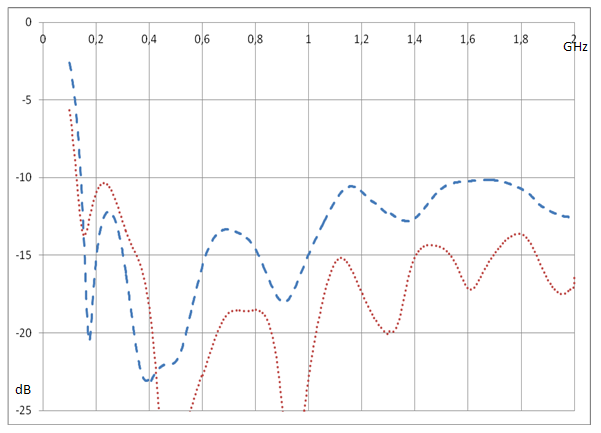
Рис. 9. Зависимость коэффициента отражения несимметричного петлевого ТЕМ рупора от частоты

Рассмотрены варианты излучателя с плоским и коническими экранами и формой петли в виде дуги окружности и овала. Коэффициент отражения несимметричного петлевого ТЕМ рупора вычислялся с помощью численной процедуры на основе метода конечных элементов. На рис. 9 приведены характеристики согласования моделей несимметричного петлевого TEM рупора с конической формой экрана– пунктирная линия и плоской – штриховая линия. На рис. 9 можно видеть, что лучшее согласование обеспечивается при коническом экране с петлей овальной формы. Данный излучатель обладает наименьшей для рассматриваемых элементов нижней частотой согласования по уровню -10 дБ (167 МГц или ka = 0.87).

Для сравнения качества согласования антенны введем коэффициент использования размера (КИР), равный отношению диаметра сферы Чу [14] для соответствующей полосы согласования к диаметру сферы, описанной вокруг антенны. Данная характеристика выражает близость нижней границы частоты согласования к пределу Чу. Значения КИРа для исследованных СШП излучателей представлены в таблице 1.

 

Таблица 1

Тип излучателя	КИР
ТЕМ рупор	0,1
МДТР	0,2
экспоненциальный ТЕМ рупор	0,5
несимметричный петлевой ТЕМ рупор	0,65

 

Как видно из таблицы, максимальное значение имеет КИР несимметричного петлевого ТЕМ рупора, который превышает КИР симметричного нерегулярного ТЕМ рупора примерно на 30% , КИР МДТР – более, чем в 3 раза, а КИР классического ТЕМ рупора – более, чем в 6 раз.

 

4.                Исследование согласования 7-элементной кольцевой решетки несимметричных петлевых TEM рупоров

В связи с полученными результатами, далее было проведено моделирование семиэлементной кольцевой антенной решетки (КАР) с общим коническим экраном, в качестве элемента которой использован оптимизированный несимметричный петлевой ТЕМ рупор с петлей овальной формы.. На рис. 10 можно видеть характеристику согласования элемента данной КАР, полученную с помощью компьютерного моделирования. Остальные элементы КАР при этом нагружены на согласованные нагрузки.

Если исключить небольшой выброс коэффициента отражения на частоте 300 МГц, то можно считать нижней границей полосы согласования по уровню -10 дБ 150 МГц.

На рис. 11 изображена экспериментально полученная зависимость коэффициент отражения КАР от частоты. Экспериментальная нижняя граница согласования примерно равна рассчитанной величине, а экспериментальная полоса согласования составляет более 1:140.

 

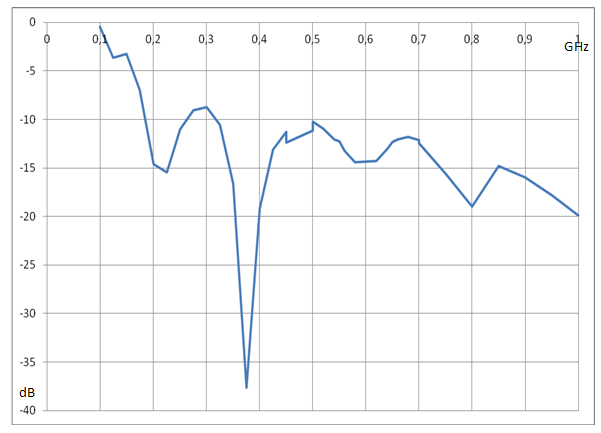
Рис. 10. Зависимость коэффициента отражения элемента КАР от частоты.

 

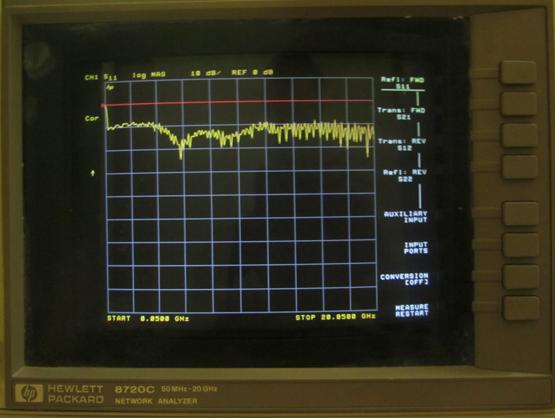
Рис. 11. Экспериментальная зависимость коэффициента отражения элемента КАР от частоты

 

 

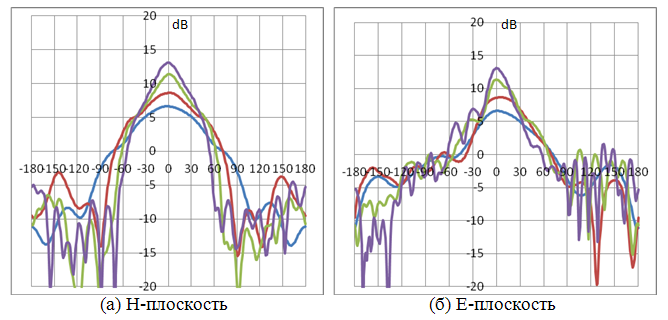
Рис. 12. Диаграммы направленности элемента решетки

 

На рис. 12 для трех частот представлены диаграммы направленности элемента решетки в E- плоскости (12а) и H-плоскости (12б). Синяя линия соответствует диаграмме направленности на частоте 0.6 ГГц, красная – 1 ГГц, зеленая – 2 ГГц и фиолетовая – 3 ГГц.

 

Работа выполнена при поддержке РФФИ (проект №12-07-00717-а).

 

Литература

1.  Ашихмин А.В.. Проектирование и оптимизация сверхширокополосных антенных устройств и систем для аппаратуры радиоконтроля, М.: «Радио и Связь», 2005, 486с.

2.  Лось В.Ф., Шаманов А.Н.. Сверхширокополосные излучатели для антенных решеток. Антенны, 2004, вып.8-9 (87-88), с.80-87.

3.       Bialkowski M.E., Abbosh A.M., Wang Y., Ireland D., Bakar A.A., Mohammed B.J. Microwave imaging systems employing cylindrical, hemispherical and planar arrays of ultrawideband antennas // Microwave Conference Proceedings (APMC-2011), (5-8 Dec. 2011, Melbourne) Asia-Pacific, pp. 191 – 194

4.       Turk A.S., Keskin A.K. Ultra wide band TEM horn antenna designs for ground penetrating impulse radar // IEEE International Conference Ultra-Wideband (ICUWB-2012), (17-20 Sept. 2012, Syracuse, New York (USA)), pp. 87 – 91

5.       Callec V., Fourn E., Gillard R., Diez, H. A new interleaved ultrawideband antenna array // 15th International Symposium Antenna Technology and Applied Electromagnetics (ANTEM-2012), (25-28 June 2012, Toulouse), pp. 1 – 4

6.       Kindt R.W. Prototype Design of a Modular Ultrawideband Wavelength-Scaled Array of Flared Notches // IEEE Transactions Antennas and Propagation, pp. 1320 – 1328

7.       Chavka G.G. Ultrawideband planar antennas and antenna arrays // 6th International Conference Ultrawideband and Ultrashort Impulse Signals (UWBUSIS-2012), (17-21 Sept. 2012, Sevastopol), pp. 9 – 14

8.       Salmani Z., Hualiang Zhang, Log-periodic antenna array inspired parallel strip ultra-wideband (UWB) antenna // IEEE Radio and Wireless Symposium (RWS-2011), (16-19 Jan. 2011), pp. 283 – 286

9.  Yan He, Chang-Hong Liang, Qing Huo Liu Novel Array EBG Structures for Ultrawideband Simultaneous Switching Noise Suppression // IEEE Antennas and Wireless Propagation Letters, Vol. 10, 2011, pp. 588 – 591

10.  Ефимова Н.А., Калошин В.А. Сверхширокополосные излучатели для кольцевых антенных решеток // Труды VI Всеросс. научн.-техн. конф. «Радиолокация и радиосвязь», М., 2012 г. Т. 2, с. 289-292

11.  Ефимова Н.А., Калошин В.А., Скородумова Е.А. Исследование рупорно-линзовой ТЕМ-антенны // РЭ, 2012, том 57, № 9, 1020-1027.

12.  Kaloshin V.A., Scattering matrix for a junction of two horns // RJMP, 2009, v. 16, No. 2, pp. 246–250.

13.  Yang F.C., Lee K.S.H. // Sensor and Simulation Notes. 1976. № 221. P. 20. URL: http://www.ece.unm.edu/suma/notes/SSN/note221.pdf

14.  Chu L.J. Physical Limitations of Omni-Directional Antennas // Journal of Applied Physics, 1948, 19, December, pp. 1163-1175