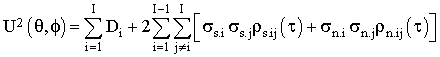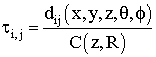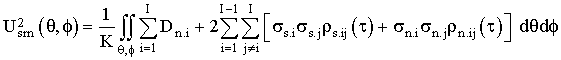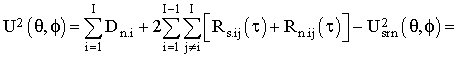Метод повышения пространственной разрешающей способности многоканальных обнаружителей сигналов, в тракте обработки которых используются сумматор, квадратор и интегратор.

УДК 621.37; 681.883.062

метод повышения пространственной разрешающей способности многоканальных обнаружителей сигналов, в тракте обработки которых используются сумматор, квадратор и интегратор

В. Н. Долгих, А. Н. Сучков, К. А. Ушаков

Филиал военного учебно-научного цента ВМФ «Военно-морская академия» (г. Владивосток)

Статья получена 23 декабря 2013 г.

Аннотация. В статье описываются результаты теоретических и имитационных исследований метода формирования откликов многоканальных пространственных фильтров, в тракте обработки которых используется сумматор, квадратор и интегратор, позволяющего повысить их пространственную разрешающую способность при малых отношениях сигнала к помехе на их входах. В результате исследований подтверждена эффективность предложенного метода по формированию направленных свойств и вероятностным характеристикам обнаружения сигнала.

Ключевые слова: отклик, пространственный фильтр, сумматор, квадратор, интегратор, отношение сигнала к помехе, имитационное моделирование.

Abstract: The paper deals with theoretical and imitating research results of formation method of multichannel dimensional filters response where summator, squarer and the integrator are used in the processing chain and allow to improve the spatial selectivity at a small ratio signal-to-noise at the inputs. As a result of the method offered the research efficiency on formation of spatial selectivity and probabilistic characteristic of signal detection was confirmed.

Key words: response, dimensional filter, summator, squarer, integrator, noise-to-signal ratio, simulation modeling.

Введение

Под пространственным фильтром (ПрФ) понимается радиотехническое средство, которое состоит из развитой в пространстве дискретной антенной решетки (ДАР), с пространственными размерами, превышающими длину волны сигнала, и тракта обработки выходных процессов приемных элементов (Э) ДАР до устройства принятия решения. В данной статье рассматривается метод формирования откликов многоканальных обнаружителей сигналов с неизвестными параметрами при произвольных типах ДАР, позволяющий повысить пространственную разрешающую способность обнаружителя.

В реальных условиях сигналы обнаруживаются на фоне помех. Наиболее сложной практической задачей является задача обнаружения сигналов, амплитуда которых на входе ДАР меньше амплитуды помех. Эта задача решается путем использования пространственной фильтрации и оптимальных методов обработки входных процессов ДАР. Теория формирования откликов оптимальных обнаружителей сигналов достаточно полно разработана в ряде работ, например, [1–4]. В соответствии с этими работами оптимальным многоканальным обнаружителем сигналов с неизвестными параметрами является пространственный фильтр, в тракте обработки которого используются сумматор, квадратор и интегратор. В связи с тем, что операция возведения выходных процессов сумматора выходных процессов Э ДАР является нелинейной операцией, далее по тексту будем называть его мультипликативным пространственным фильтром (МПрФ). Отклик МПрФ на смесь сигнала и помехи можно описать, используя известный подход.

1. Принцип формирования отклика мультипликативного пространственного фильтра

Пусть ДАР состоит из I элементов, расположенных в пространстве произвольным образом; на ДАР падает плоская волна случайного гауссового шумового сигнала с нулевым средним, пространственное направление сигнала характеризуется углом падения q и азимутальным углом j; на входе Э наблюдается аддитивная смесь сигнала с гауссовой помехой с нулевым средним. Если координаты Э известны с заданной точностью на момент формирования отклика ПрФ, то отклик МПрФ на аддитивную смесь сигнала и помехи можно представить в следующем виде:

, (1)

где ( - временная задержка обусловленная направлением прихода сигнала и пространственным разнесением Э; - компенсационная временная задержка);

- эффективные значения сигнала и помехи на выходе - го Э ДАР;

- дисперсия смеси сигнала и помехи на выходе - го канала, в силу статистической независимости сигнала и помехи.

В выражении (1) от пространственных углов и пространственного разнесения приемника зависят величины временной задержки процессов на выходах Э ДАР:

, (2)

где - разность расстояний между -м и -м приемниками, входящими в состав ДАР, в пространстве, являющаяся функцией координат приемников x, y, z и пространственных углов прихода сигналов q, j (q – угол падения, j - азимутальный угол);

С(z, R) - скорость распространения волн (R – координата точки наблюдения в горизонтальной плоскости, z – координата точки наблюдения в вертикальной плоскости).

Откуда следует, что изменение расстояния между Э ДАР является аналогом изменения временной задержки между сигналами. Эта зависимость в формуле (1) и последующих формулах для упрощения записи формул опущена.

Анализ формулы (1) показывает, что отклик МПрФ состоит из двух составляющих: постоянной составляющей, определяемой суммой дисперсий сигналов и помех; переменной составляющей, определяемой корреляционными свойствами сигналов и помех. Наличие постоянной составляющей приводит к тому, что при уменьшении отношения сигнала к помехе (ОСП) уровень бокового поля отклика МПрФ возрастает до значений, при которых определение направления на источник сигналов становится невозможным. Кроме того, увеличиваются угловые размеры остроты направленного действия и ширины главного максимума отклика ПрФ, что уменьшает разрешающую способность источников сигнала по пространству. Естественно, что в интересах повышения разрешающей способности по пространству МПрФ из его отклика необходимо вычесть постоянную составляющую [5,6]. Однако при этом можно потерять и полезную информацию о сигнале, содержащуюся в дисперсионной составляющей сигнала, что может повлиять на вероятностные характеристики обнаружения сигнала на фоне помех.

Поэтому возможным решением проблемы повышения разрешающей способности МПрФ в пространстве является использование операции вычитания среднего по области обзора пространства значения отклика МПрФ на помеху [7]:

, (3)

где - дисперсия помех на выходе - го Э ДАР.

Тогда формула (1) с учетом независимости дисперсии помех от пространственных углов обзора пространства примет вид

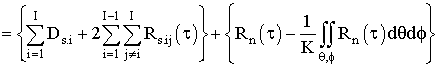, (4)

где - функции взаимной корреляции сигналов и помех на выходах -го и -го Э ДАР;

- дисперсия сигналов и помех на выходе i-го преобразователя;

- суммарная корреляционная функция помех;

- усредняющий множитель, ;

- сектор углов обзора пространства в вертикальной плоскости, ;

- сектор углов обзора пространства в горизонтальной плоскости, .

Из выражения (4) следует, что дисперсионная составляющая помехи может быть полностью подавлена; постоянная составляющая переменной части помехи вычитается из переменной части помехи. Это неизбежно приведет к уменьшению влияния помехи на направленные свойства МПрФ.

Естественно возникает вопрос: «Каким образом в реальных условиях получить оценку выражения (3)?». Ответ на этот вопрос заключается в том, что ее можно получить до момента обнаружения цели, а после принятия решения об обнаружении сигнала и последующем слежении за ним использовать полученную оценку среднего уровня помехи по области обзора пространства при оценке откликов МПрФ по алгоритму (4) в разные моменты времени. В процессе слежения за сигналом могут возникать отклонения пространственного среднего уровня помех, обусловленные физической сущностью их формирования в среде распространения. Оценку влияния флуктуаций среднего уровня помех на эффективность пространственного разрешения сигнала и вероятность его обнаружения проще всего провести с использованием имитационного моделирования откликов МПрФ и вероятностных характеристик обнаружения сигнала.

2. Имитационное моделирование откликов мультипликативных пространственных фильтров

Для этого авторами статьи был разработан комплекс программ, позволяющий решать эти задачи. Суть методики моделирования заключалась в том, что моделировались ДАР, тракты обработки МПрФ входные шумовые сигналы, приходящие с заданного пространственного направления, и помехи, представляющие собой гауссовые процессы с нулевым средним. На основе этих моделей проводилось формирование откликов МПрФ в соответствии с рассмотренными алгоритмами (1), (4) и оценка эмпирических функций распределения вероятностей их откликов на аддитивную смесь сигналов и помех и помеху с определенного в процессе формирования отклика пространственного направления прихода сигнала, которые использовались для определения вероятностных характеристик обнаружения сигнала. Программа моделирования позволяет производить имитационные исследования откликов ПрФ на смесь сигналов и помех. Ниже приведены результаты исследования откликов ПрФ на гидроакустические процессы с длинами волн от 0,25 до 1,5 м. Основные выводы, результаты исследования и закономерности формирования откликов справедливы и для радиочастотного диапазона.

В качестве модели ДАР использовалась модель цилиндрической звукопрозрачной антенной решетки с 64 электроакустическими преобразователями (ЭАП), расположенных случайным образом по ее поверхности. Использование стохастической антенной решетки позволило сократить время, затрачиваемое на моделирование в несколько раз. Гистограммы распределения вероятностей оценивались по результатам анализа 101 реализации смеси и помехи. На первом цикле работы программы оценки вероятностных характеристик определялась величина среднего значения помехи по области обзора пространства, которая использовалась для оценки откликов МПрФ в последующих 101 циклах формирования откликов МПрФ по алгоритму (4). Все исходные данные и модели входных процессов при разных методах формирования откликов МПрФ были идентичными. Флуктуации ОСП на входе ДАР находились в интервале примерно равном 1 дБ.

На рис. 1 представлены примеры оценки сечений откликов МПрФ в горизонтальной и вертикальной плоскостях для смеси сигнала с помехой и сигнала.

Из рис. 1 следует, что при реализации алгоритма (4) ширина главного максимума и острота направленного действия ПрФ практически совпадают с аналогичными параметрами отклика МПрФ, сформированного по алгоритму (1), на сигнал в отсутствии помех. Переменная по области обзора пространства составляющая помехи в основном влияет на уровень бокового поля отклика и по своей величине значительно меньше уровня бокового поля отклика классического МПрФ. Откуда следует, что использование алгоритма (4) приводит к значительному снижению влияния помех на направленные свойства ПрФ.

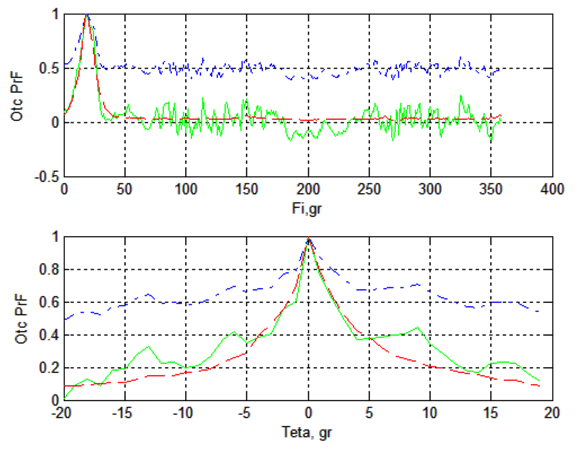
Рис. 1. Сечения нормированных откликов МПрФ (алгоритм (1))

на смесь (синяя штрихпунктирная линия), на сигнал (красная пунктирная линия) и МПрФ, отклик которого сформирован по алгоритму (4), на смесь (зеленая сплошная линия) в горизонтальной (верхний рисунок) и вертикальной (нижний рисунок) плоскостях. ОСП = –19 дБ.

Пример трехмерного представления отклика ПрФ сформированного по алгоритму (4), представлен на рис. 2.

Из рис. 2 следует, что при ОСП равном –15,5 дБ в отклике МПрФ на смесь, есть один боковой максимум с максимальной величиной примерно равной 0,4. Следует заметить, что величина и пространственное положение максимальных значений бокового поля отклика изменяются от реализации к реализации.

Малые значения бокового поля отклика МПрФ на сигнал обусловлены удачным пространственным расположением ЭАП в ДАР, достаточным их числом [8] и широкой полосой входных процессов. В нашем случае уровень боковых максимумов отклика на сигнал менее 0,1, что можно оценить выражением . Следует заметить, что величина боковых максимумов отклика МПрФ на смесь тем больше, чем меньше ОСП на входе ДАР.

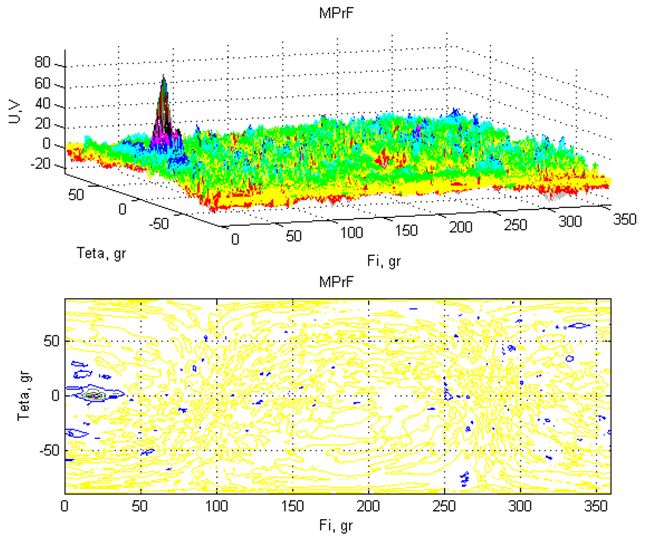
Рис. 2. Трехмерный отклик МПрФ, отклик которого сформирован по алгоритму (4), на смесь (верхний рисунок) и его контурное изображение (нижний рисунок). ОСП = –15,5 дБ.

Пример результатов оценки гистограмм распределения вероятности и вероятностных характеристик обнаружений сигнала представлен на рис. 3 и рис. 4.

На рис. 3 теоретические кривые распределения плотности вероятности рассчитаны для гауссовых процессов с параметрами математического ожидания и дисперсии, определенными в процессе моделирования.

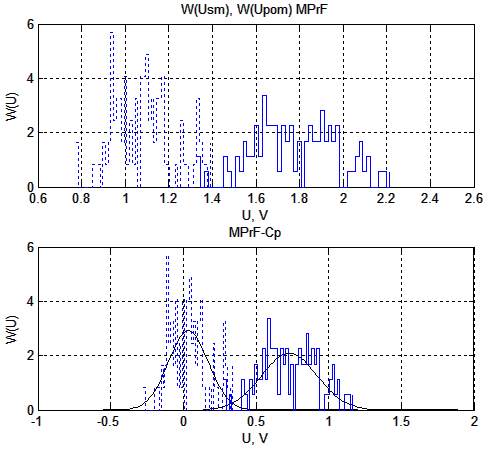
Рис. 3. Гистограммы распределения плотности вероятности помехи (ступенчатая пунктирная линия), смеси сигнала с помехой (ступенчатая сплошная линия) и теоретическая кривая плотности распределения вероятности (сплошная плавная линия) для МПрФ (верхний рисунок) и МПрФ при вычитании из его отклика среднего значения помехи в области обзора пространства.

ОСП = –17,68 дБ, объем выборки 1024 значения.

В результате моделирования установлено, что абсолютное значение порога принятия решения об обнаружении сигнала при использовании алгоритма формирования отклика МПрФ (4) значительно меньше, чем в случае формирования отклика по алгоритму (1), что объясняется уменьшением дисперсии смеси сигнала и помехи. Значительные флуктуации эмпирических функций обусловлены конечностью усредняемых выборок и флуктуациями дисперсий входных процессов обнаружителя от реализации к реализации. При увеличении объема усредняемых выборок и их числа эмпирические функции распределения вероятностей стремятся к теоретическим (гауссовым).

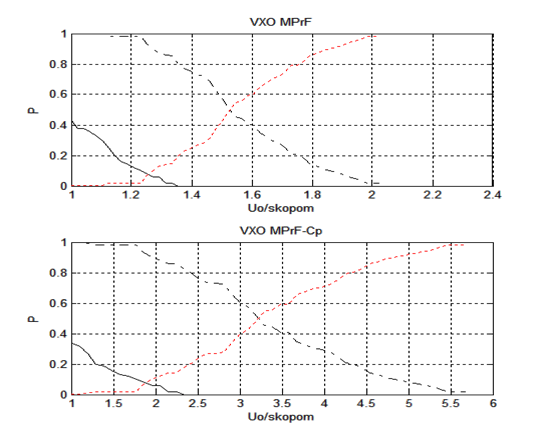
Рис. 4. Вероятностные характеристики обнаружения сигнала МПрФ (верхний рисунок) и МПрФ, из отклика которого вычитается среднее по области обзора пространства значение помехи; вероятность обнаружения (штрихпунктирная линия); вероятность ложной тревоги (сплошная линия); вероятность пропуска сигнала (пунктирная линия).

ОСП = –17,5 дБ, объем выборки 512 значений.

Оценка вероятностных характеристик обнаружения сигнала при использовании двух рассмотренных алгоритмов формирования откликов показала, что при заданной величине вероятности ложной тревоги относительный порог обнаружения (отношение порога к эффективному значению помехи на входе устройства принятия решения) при использовании алгоритма (4) в полтора-два раза больше, чем при использовании первого алгоритма. Это связано с тем, что при втором алгоритме величина дисперсии помехи значительно меньше, чем при первом алгоритме (см. рис. 3). При этом вероятностные характеристики обнаружения сигналов, учитывая погрешности оценки вероятностей, примерно равны. Например, по результатам, представленным на рис. 4, вероятность обнаружения сигнала при величине вероятности ложной тревоги 0,01 для МПрФ, отклик которого сформирован по алгоритму (1), равна 0,82, а для МПрФ, отклик которого сформирован по алгоритму (4), – 0,84. При этом величина вероятности пропуска сигнала менее 0,2.

Выводы

На основании выполненных исследований можно утверждать, что предложенный метод формирования отклика обнаружителя позволяет повысить пространственную разрешающую способность при малых отношениях сигнала к помехе и является достаточно эффективным.

Литература

1. Тихонов В. И. Статистическая радиотехника. – М.: Сов. Радио, 1966. – 678 с.

2. Левин Б.Р. Теоретические основы статистической радиотехники. – М.: Сов. Радио, 1975. – 391 с.

3. Ван Трис Г. Теория обнаружения, оценок и модуляции. – М.: Советское радио, 1972. – 744 с.

4. Тюрин А. М. Введение в теорию статистических методов в гидроакустике. - Л.: ВМОЛУА, 1963. – 251 с.

5. Долгих В.Н., Бородин А.Е. Высокопроизводительный метод корреляционной обработки информации в пространственном фильтре акустических сигналов // Сборник трудов XI сессии РАО, т. 2, с.22…25. – М.: ГЕОС, 2001.

6. Долгих В.Н., Бородин А.Е., Ламека А.П. Устройство с корреляционным формирователем характеристики направленности для обнаружения сигналов и определения направления на их источник // Патент на изобретение № 2305297. – Российское агентство по патентам и товарным знакам, 2007.

7. Долгих В.Н., Ушаков К.А. Устройство для обнаружения сигналов и определения направления на их источник // Патент на изобретение № 2499276. – Российское агентство по патентам и товарным знакам, 2013.

8. Кремер И.Я., Кремер А.И., Петров В.М., Понькин В.А., Потапов Н.А. Пространственно-временная обработка сигналов. – М.: Радио и связь, 1984. – 223 с.