УДК 537.862
РАСТАЛКИВАНИЕ РЕЗОНАНСНЫХ ЧАСТОТ МАГНИТОДИНАМИЧЕСКИХ КОЛЕБАНИЙ В НАМАГНИЧЕННЫХ ФЕРРИТОВЫХ РЕЗОНАТОРАХ МИЛЛИМЕТРОВОГО ДИАПАЗОНА
Н. Н. Мовчан, М. А. Попов
Киевский национальный университет имени Тараса Шевченко
Статья получена 26 декабря 2013 г.
Аннотация. В работе исследовано расталкивание резонансных частот магнитодинамических колебаний в ферритовых резонаторах миллиметрового диапазона в форме диска и прямоугольного параллелепипеда. В частности, теоретически и экспериментально исследовано начальное расталкивание резонансных частот магнитодинамических колебаний в малых магнитных полях. В результате численных расчетов с помощью пакета программ HFSS обнаружено, что в условиях эксперимента преобладающей причиной начального расталкивания резонансных частот в дисковом ферритовом резонаторе является нарушение цилиндрической симметрии электромагнитного поля вокруг резонатора при его помещении, как неоднородности, в волновод. Предложена методика управления величиной начального расталкивания резонансных частот ферритового резонатора в форме прямоугольного параллелепипеда путем изменения формы резонатора. Экспериментально показана возможность уменьшения начального расталкивания резонансных частот с 1 ГГц до 400 МГц и увеличения модуля крутизны полевой зависимости частот колебаний ЖИГ резонаторов в области малых полей (~100-200 Э) от 0.5 МГц/Э до 1 МГц/Э.
Ключевые слова: ферритовый резонатор, магнитная перестройка, магнитодинамические колебания, железо-иттриевый гранат.
Abstract. In the paper the repulsion of the magnetodynamic modes resonant frequency in the ferrite disc-shaped and rectangular parallelepiped-shaped millimeter band resonators have been investigated. In particular, the initial repulsion of magnetodynamic modes eigenfrequencies at low magnetic fields was studied both theoretically and experimentally. From numerical calculations using the HFSS software package it was found that for the current experimental conditions the predominant cause of the resonance frequencies initial repulsion in the disk-shaped ferrite resonator is the distortion of the cylindrical symmetry of the electromagnetic field around the resonator when it is placed as inhomogeneity inside the waveguide. A method was proposed to control the magnitude of the resonance frequencies initial repulsion of the ferrite rectangular parallelepiped-shaped resonator by changing the shape of the resonator. The possibility of reducing the resonance frequencies initial repulsion from 1 GHz to 400 MHz and increasing the magnitude steepness of the frequency vs. field dependence of the YIG resonators in low fields (~ 100-200 Oe) from 0.5 MHz/Oe to 1 MHz/Oe was experimentally demonstrated.
Keywords: ferrite resonator, magnetic tuning, magnetodynamic modes, yttrium iron garnet.
Введение
Среди управляемых твердотельных приборов
миллиметрового диапазона [1-4] особый практический интерес представляют приборы, использующие собственные колебания ферритовых
резонаторов [5-10]. Намагниченные ферритовые резонаторы позволяют в одном и том
же образце объединить свойства магнитогиротропного и диэлектрического резонатора.
При намагничивании ферритового резонатора наблюдается расталкивание его
резонансных частот. Управление резонансными частотами ферритового магнитодиэлектрического
резонатора магнитным полем позволяет получить сравнительно большую крутизну зависимости рабочей частоты прибора от
магнитного поля (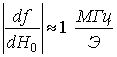 ) для ненасыщенного состояния
ферритового образца. Магнитное управление резонансной частотой магнитодинамических
колебаний ферритового резонатора позволяет использовать слабоанизотропные ферриты
с малыми диэлектрическими потерями, предназначенные для сантиметрового
диапазона, например, железо-иттриевый гранат (ЖИГ), в миллиметровом и
субмиллиметровом диапазоне наравне с
гексаферритами, которые имеют большое поле одноосной кристаллографической
анизотропии.
) для ненасыщенного состояния
ферритового образца. Магнитное управление резонансной частотой магнитодинамических
колебаний ферритового резонатора позволяет использовать слабоанизотропные ферриты
с малыми диэлектрическими потерями, предназначенные для сантиметрового
диапазона, например, железо-иттриевый гранат (ЖИГ), в миллиметровом и
субмиллиметровом диапазоне наравне с
гексаферритами, которые имеют большое поле одноосной кристаллографической
анизотропии.
Ранее были исследованы магнитодинамические колебания в резонаторах из железо-иттриевого граната [5], гексаферрита бария [6], [7], а также были предложены макеты фильтров [8], фазовращателей [9], вентилей [10] на эффекте расталкивания резонансных частот.
Согласно аналитической теории магнитодинамических колебаний в намагниченных ферритовых резонаторах цилиндрической формы [7] в ненамагниченном состоянии феррита расталкивание резонансных частот отсутствует. Колебания с правой и левой циркулярными поляризациями и одинаковыми по модулю азимутальным и радиальным индексами являются вырожденными по частоте. Однако, практически во всех экспериментах, когда ферритовый резонатор включался, как неоднородность, в линию передачи, было зафиксировано начальное расталкивание резонансных частот колебаний при отсутствии поля подмагничивания. Эффект начального расталкивания резонансных частот значительно уменьшает крутизну частотно-полевой зависимости магнитодинамических колебаний ЖИГ резонаторов в области малых полей (~100-200 Э).
Ранее начальное расталкивание резонансных частот объяснялось на качественном уровне наличием недиагональных компонент тензора магнитной проницаемости ферритовых образцов с малым количеством доменов [11] или связью между собственными колебаниями ферритового резонатора, размещенного на металлической стенке волновода, через поверхностный импеданс металла [9, 12]. Однако выдвинутые гипотезы не дают количественно объяснения величины начального расталкивания резонансных частот.
Снятие вырождения по частоте колебаний дискового ферритового резонатора также может быть вызвано влиянием элементов линии передачи [15], например, боковых стенок волновода.
Стоит отметить, что ранее не проводился полный электродинамический анализ расталкивания резонансных частот колебаний ферритовых резонаторов при их намагничивании, а предложенные объяснения природы начального расталкивания резонансных частот носят оценочный характер.
Следуя теории связанных колебаний в динамической системе с двумя степенями свободы [13], для реализации максимально эффективной перестройки резонансных частот магнитодинамических колебаний ферритовых резонаторов магнитным полем необходимо равенство резонансных частот колебаний при отсутствии поля подмагничивания, или иными словами, нужно уменьшить начальное расталкивание резонансных частот. Оптимизацию СВЧ системы с ферритовым резонатором для минимизации начального расталкивания резонансных частот сложно осуществить аналитическими методами, поэтому для решения этой задачи было использовано численное решение уравнений Максвелла с помощью метода конечных элементов реализованным для случая пассивных СВЧ цепей с ферритовыми включениями в пакете программ HFSS 13 фирмы Ansoft.
Целью данной работы является теоретическое и экспериментальное исследование расталкивания резонансных частот в намагниченных ферритовых резонаторах миллиметрового диапазона имеющих форму диска и прямоугольного параллелепипеда, а также выяснение причин начального расталкивания резонансных частот ферритовых резонаторов.
1. Эффект начального расталкивания резонансных частот магнитодинамических колебаний в дисковых ферритовых резонаторах
Ранее проведенные исследования расталкивания резонансных частот колебаний в дисковых ЖИГ резонаторах [5,8,9] показали, что расталкивание резонансных частот существует и при отсутствии поля подмагничивания.
Для
теоретической интерпретации начального расталкивания резонансных частот
колебаний [5] в программе HFSS 13 была смоделирована измерительная ячейка с
дисковым резонатором из монокристалла ЖИГ. При расчетах полагалось, что ЖИГ
резонатор, который имеет радиус 0.8 мм и высоту 0.45 мм, расположен в отрезке
волновода прямоугольного сечения U-диапазона (4.77×2.39 ![]() ) длиной 5 см, посредине широкой стенки
волновода, симметрично относительно боковых стенок. Стенки волновода рассматривались
как металл с конечной проводимостью – серебро. В HFSS модели исследуемый отрезок
волновода возбуждался основной модой прямоугольного волновода
) длиной 5 см, посредине широкой стенки
волновода, симметрично относительно боковых стенок. Стенки волновода рассматривались
как металл с конечной проводимостью – серебро. В HFSS модели исследуемый отрезок
волновода возбуждался основной модой прямоугольного волновода ![]() через два волноводных порта. Удовлетворительная
точность расчета частотных зависимостей S-параметров была получена при
разбиении исследуемой СВЧ конструкции на 15 тыс. тетраэдров.
через два волноводных порта. Удовлетворительная
точность расчета частотных зависимостей S-параметров была получена при
разбиении исследуемой СВЧ конструкции на 15 тыс. тетраэдров.
В соответствии с результатами измерения петли гистерезиса ЖИГ резонатора с помощью СКВИД магнитометра [5] при расчетах в HFSS была использована кусочно-линейная аппроксимация кривой намагничивания ЖИГ и магнитного поля внутри образца:
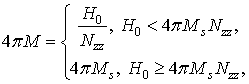
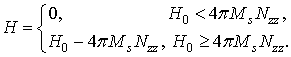 (1)
(1)
где ![]() −
напряженность поля подмагничивания,
−
напряженность поля подмагничивания, ![]() − напряженность магнитного поля внутри
резонатора,
− напряженность магнитного поля внутри
резонатора, ![]() −
намагниченность ферритового резонатора,
−
намагниченность ферритового резонатора, ![]() − намагниченность насыщения. Размагничивающий
фактор вдоль оси резонатора
− намагниченность насыщения. Размагничивающий
фактор вдоль оси резонатора ![]() рассчитывался согласно [14].
рассчитывался согласно [14].
При
расчете были использованы такие параметры монокристалла ЖИГ: намагниченность
насыщения ![]() , ширина линии ФМР
, ширина линии ФМР ![]() ,
тангенс угла диэлектрических потерь
,
тангенс угла диэлектрических потерь ![]() . Наилучшее
согласование расчетных S-параметров с результатами эксперимента [5] в широкой
полосе частот получено при диэлектрической проницаемости монокристалла ЖИГ
. Наилучшее
согласование расчетных S-параметров с результатами эксперимента [5] в широкой
полосе частот получено при диэлектрической проницаемости монокристалла ЖИГ ![]() . Поле магнитной кристаллографической
анизотропии при моделировании не учитывалось.
. Поле магнитной кристаллографической
анизотропии при моделировании не учитывалось.
В
результате расчетов получены частотные зависимости коэффициента передачи ![]() исследуемой СВЧ конструкции для разных
значений внешнего поля подмагничивания и полевая зависимость резонансных частот
магнитодинамических колебаний
исследуемой СВЧ конструкции для разных
значений внешнего поля подмагничивания и полевая зависимость резонансных частот
магнитодинамических колебаний ![]() и
и ![]() дискового
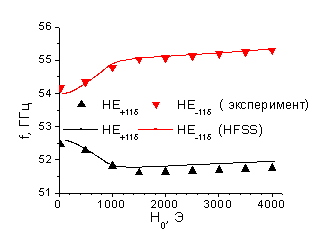
ЖИГ резонатора. Сравнение теоретического расчета и экспериментальных данных [5]
показано на рис.1.
дискового
ЖИГ резонатора. Сравнение теоретического расчета и экспериментальных данных [5]
показано на рис.1.

а) б)
Рис. 1. Сравнение теоретических и экспериментальных а)
зависимостей резонансных частот от магнитного поля; б) частотных зависимостей коэффициента
передачи ![]() для
колебаний
для
колебаний ![]() и
и
![]() дискового
ЖИГ резонатора.
дискового
ЖИГ резонатора.
Классификация
типов колебаний на рис. 1 проведена согласно работе [7]. Теоретический расчет
для колебания ![]() проведен для магнитных полей
проведен для магнитных полей ![]() , поскольку для меньших
величин подмагничивающего поля колебание
, поскольку для меньших
величин подмагничивающего поля колебание ![]() имеет
очень малый коэффициент связи с прямоугольным волноводом и его резонансная
линия не наблюдается на фоне резонансной линии колебания
имеет
очень малый коэффициент связи с прямоугольным волноводом и его резонансная
линия не наблюдается на фоне резонансной линии колебания ![]() .
.
Отметим
хорошее совпадение теоретических и экспериментальных зависимостей (рис. 1). Некоторое
расхождение между теоретическими и экспериментальными частотными зависимостями
коэффициента передачи ![]() (рис. 1б) объясняется незначительными отклонениями
размеров резонатора от принятых при расчете и отсутствием учета
неоднородности внутреннего магнитного поля в объеме ферритового образца
неэллипсоидальной формы.
(рис. 1б) объясняется незначительными отклонениями
размеров резонатора от принятых при расчете и отсутствием учета
неоднородности внутреннего магнитного поля в объеме ферритового образца
неэллипсоидальной формы.
При
отсутствии подмагничивания ферритовый резонатор может быть рассмотрен как
эквивалентный диэлектрический резонатор. Собственные колебания дискового диэлектрического резонатора в неограниченном
пространстве с одинаковыми радиальным и азимутальным индексами, но
ортогональными угловыми зависимостями ![]() и
и ![]() , вырождены
по частоте. При помещении резонатора в волновод азимутальная симметрия системы
нарушается, вырождение колебаний снимается, и возникают два колебания с
различными резонансными частотами: четное
, вырождены
по частоте. При помещении резонатора в волновод азимутальная симметрия системы
нарушается, вырождение колебаний снимается, и возникают два колебания с
различными резонансными частотами: четное ![]() и нечетное
и нечетное ![]() относительно плоскости
симметрии проходящей через ось цилиндрической симметрии резонатора и
продольную ось волновода [15]. При намагничивании ферритового резонатора
колебания
относительно плоскости
симметрии проходящей через ось цилиндрической симметрии резонатора и
продольную ось волновода [15]. При намагничивании ферритового резонатора
колебания ![]() и
и ![]() переходят
в магнитодинамические колебания
переходят
в магнитодинамические колебания ![]() и
и ![]() соответственно. Расчет в HFSS (рис. 1а) предсказывает существование начального
расталкивания резонансных частот колебаний
соответственно. Расчет в HFSS (рис. 1а) предсказывает существование начального
расталкивания резонансных частот колебаний ![]() и
и ![]() при малых
значениях магнитного поля.
при малых
значениях магнитного поля.
Преобладающей, в условиях эксперимента [5], причиной снятия вырождения колебаний при отсутствии поля подмагничивания является нарушение цилиндрической симметрии электромагнитного поля вокруг резонатора при помещении его в прямоугольный волновод. Стоит также отметить, что в начальное расталкивание резонансных частот в ферритовом резонаторе вносят вклад наличие остаточной намагниченности и связь колебаний через поверхностный импеданс металлической поверхности, на которой лежит резонатор (учитывается при расчете в HFSS через импедансные граничные условия на стенках волновода). Однако в условиях эксперимента [5] их вклады не являются доминирующими.
2. Расталкивание резонансных частот магнитодинамических колебаний ферритовых резонаторов в форме прямоугольного параллелепипеда
Особый практический интерес представляет экспериментальное и теоретическое исследование эффекта расталкивания резонансных частот в ферритовых резонаторах имеющих форму прямоугольного параллелепипеда. Преимуществом резонаторов такой формы является простота изготовления в миллиметровом диапазоне длин волн.
Рассмотрим
ферритовый резонатор в форме прямоугольного параллелепипеда, высота ![]() которого в несколько раз меньше размеров
основания
которого в несколько раз меньше размеров
основания ![]() и
и ![]() . Резонатор
расположен на широкой стенке прямоугольного волновода, как показано на рис. 2.
. Резонатор
расположен на широкой стенке прямоугольного волновода, как показано на рис. 2.
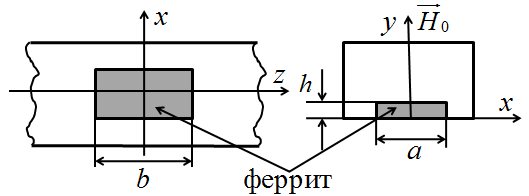
Рис. 2 Расположения ферритового образца в поперечном сечении прямоугольного волновода.
При
рассеянии моды ![]() прямоугольного волновода на ферритовом резонаторе
возбуждаются колебания типа
прямоугольного волновода на ферритовом резонаторе
возбуждаются колебания типа ![]() , где
, где ![]() соответствует количеству вариаций поля
вдоль оси
соответствует количеству вариаций поля
вдоль оси ![]() ,
, ![]() –
вдоль оси
–
вдоль оси ![]() ,
, ![]() –
вдоль оси
–
вдоль оси ![]() (направления осей координат показаны на
рис. 2). Поскольку ферритовый резонатор размещен на металлической стенке
волновода и частично заполняет его поперечное сечение по высоте, то в
эксперименте наблюдаются только нижайшие моды с
(направления осей координат показаны на
рис. 2). Поскольку ферритовый резонатор размещен на металлической стенке
волновода и частично заполняет его поперечное сечение по высоте, то в
эксперименте наблюдаются только нижайшие моды с ![]() . Классификация
типов колебаний проводится согласно пространственным распределениям
электрического и магнитного полей колебаний полученных в программе HFSS.
. Классификация
типов колебаний проводится согласно пространственным распределениям
электрического и магнитного полей колебаний полученных в программе HFSS.
В
случае, когда размеры основания резонатора ![]() и
и ![]() незначительно отличаются между собой, два
нижайших колебания
незначительно отличаются между собой, два
нижайших колебания ![]() и
и ![]() являются
близкими по частоте. При намагничивании резонатора они становятся
связанными и их резонансные частоты расталкиваются.
являются
близкими по частоте. При намагничивании резонатора они становятся
связанными и их резонансные частоты расталкиваются.
Для
экспериментального исследования влияния линейных размеров резонатора на расталкивание
резонансных частот колебаний ![]() и
и ![]() было изготовлено три резонатора из
поликристаллического ЖИГ марки 10СЧ6Б4 в форме прямоугольного параллелепипеда.
Намагниченность насыщения ЖИГ составляет
было изготовлено три резонатора из
поликристаллического ЖИГ марки 10СЧ6Б4 в форме прямоугольного параллелепипеда.
Намагниченность насыщения ЖИГ составляет ![]() ,
ширина линии ФМР
,
ширина линии ФМР ![]() , тангенс угла
диэлектрических потерь
, тангенс угла
диэлектрических потерь ![]() . Размеры резонаторов: 1.98×1.85×0.55
. Размеры резонаторов: 1.98×1.85×0.55 ![]() (резонатор №1), 1.98×1.55×0.56
(резонатор №1), 1.98×1.55×0.56
![]() (резонатор №2), 1.98×1.4×0.55
(резонатор №2), 1.98×1.4×0.55
![]() (резонатор №3). Далее в тексте отдельные
резонаторы обозначаются только номером.
(резонатор №3). Далее в тексте отдельные
резонаторы обозначаются только номером.
В эксперименте резонаторы помещались в измерительную ячейку в виде отрезка прямоугольного волновода U-диапазона, как показано на рис. 2. Поле намагничивания было приложено вдоль нормали к широкой стенке волновода. СВЧ измерения проводились с использованием векторного анализатора СВЧ-цепей Agilent E8361A.
Для
каждого из резонаторов была измерена полевая зависимость резонансных частот
нижайших магнитодинамических колебаний ![]() и
и ![]() в диапазоне магнитного поля от 0 до 2,5 кЭ.
в диапазоне магнитного поля от 0 до 2,5 кЭ.
Интерпретация
экспериментальных результатов, была проведена с помощью пакета программ HFSS 13.
Наилучшее согласование расчетных S-параметров с результатами эксперимента в
широкой полосе частот получено при диэлектрической проницаемости поликристаллического
ЖИГ ![]() .
.
Сравнение экспериментальных и теоретических зависимостей показано на рис. 3. Теоретические зависимости изображены в виде сплошных линий, экспериментальные результаты – точками.
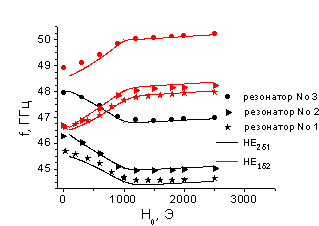
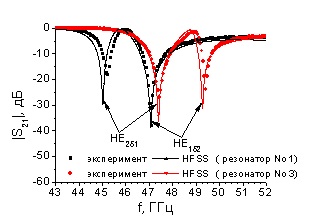
а) б)
Рис.
3. Сравнение экспериментальных и теоретических зависимостей а) резонансных
частот от магнитного поля для резонаторов №1-3; б) коэффициента передачи ![]() для измерительной ячейки с резонаторами
№1 и №3 при магнитном поле 600 Э.
для измерительной ячейки с резонаторами
№1 и №3 при магнитном поле 600 Э.
Расчет в HFSS достаточно хорошо
описывает экспериментальные частотно-полевые зависимости (рис. 3а). Исследованные
ферритовые резонаторы в форме прямоугольного параллелепипеда обеспечивают такой
же диапазон магнитной перестройки резонансных частот, как и резонаторы в форме диска.
При некотором соотношении геометрических размеров резонатора в форме параллелепипеда
можно достичь минимума начального расталкивания резонансных частот колебаний ![]() и
и ![]() . Так, для резонатора №2 на рис. 3а
начальное расталкивание резонансных частот составляет 400 МГц, в то же время
начальное расталкивание резонансных частот для резонаторов №1и №3 составляет
около 1 ГГц.
. Так, для резонатора №2 на рис. 3а
начальное расталкивание резонансных частот составляет 400 МГц, в то же время
начальное расталкивание резонансных частот для резонаторов №1и №3 составляет
около 1 ГГц.
На рис. 3б показано сравнение
экспериментальных и рассчитанных в HFSS частотных зависимостей коэффициента
передачи ![]() измерительной ячейки с ферритовыми
резонаторами №1 и №3 при поле подмагничивания
измерительной ячейки с ферритовыми
резонаторами №1 и №3 при поле подмагничивания ![]() . Следует
отметить, что практическое использование колебания
. Следует
отметить, что практическое использование колебания ![]() при
магнитном поле
при
магнитном поле ![]() невозможно, вследствие очень слабой
связи резонатора с модой
невозможно, вследствие очень слабой
связи резонатора с модой ![]() прямоугольного волновода.
прямоугольного волновода.
Для управления начальным расталкиванием резонансных частот магнитодинамических колебаний ферритовых резонаторов предложено изменять ширину резонатора.
С помощью пакета программ HFSS была
исследована зависимость расталкивания резонансных частот ЖИГ резонатора в форме
прямоугольного параллелепипеда от отношения поперечных размеров его основания
при магнитном поле ![]() . На рис. 4 показано сравнение теоретического
расчета в HFSS с результатами эксперимента для резонаторов №1-3. При расчетах
было принято, что длина наибольшей грани резонатора
. На рис. 4 показано сравнение теоретического
расчета в HFSS с результатами эксперимента для резонаторов №1-3. При расчетах
было принято, что длина наибольшей грани резонатора ![]() , толщина
h=0.56 мм, а ширина резонатора
, толщина
h=0.56 мм, а ширина резонатора ![]() (см. рис. 2) рассматривалась
как независимая переменная.
(см. рис. 2) рассматривалась
как независимая переменная.
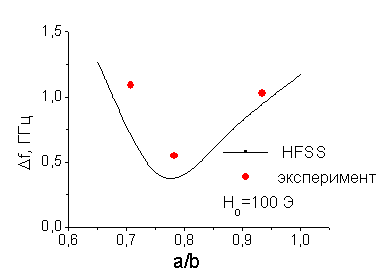
Рис.
4. Сравнение экспериментальной и теоретической зависимости расталкивания
резонансных частот колебаний ![]() и
и ![]() от отношения геометрических
размеров резонатора.
от отношения геометрических
размеров резонатора.
Экспериментальные и теоретические
зависимости на рис. 4 качественно совпадают, причины количественного отличия
зависимостей те же что и в разделе 1. Минимальному расталкиванию резонансных
частот при заданном магнитном поле соответствует минимальное начальное
расталкивание резонансных частот при отсутствии поля подмагничивания (см.
зависимости для резонатора №2 на рис. 3а). На рис. 4 экспериментально и путем
численных расчетов показано существование минимума на зависимости начального
расталкивания резонансных частот колебаний ![]() и
и ![]() ферритового резонатора
в форме прямоугольного параллелепипеда от отношения поперечных размеров
резонатора.
ферритового резонатора
в форме прямоугольного параллелепипеда от отношения поперечных размеров
резонатора.
При сравнении крутизны
частотно-полевой зависимости в области малых магнитных полей (![]() ~100-200 Э) для резонаторов №1-3 найдено,
что модуль крутизны частотно-полевой зависимости для резонатора №2, размеры
которого соответствуют минимуму зависимости на рис. 4, составляет
~100-200 Э) для резонаторов №1-3 найдено,
что модуль крутизны частотно-полевой зависимости для резонатора №2, размеры
которого соответствуют минимуму зависимости на рис. 4, составляет 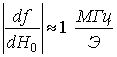 . В то же время, для резонаторов №1 и №3 модуль
крутизны частотно-полевой зависимости практически в два раза меньше и
составляет
. В то же время, для резонаторов №1 и №3 модуль
крутизны частотно-полевой зависимости практически в два раза меньше и
составляет 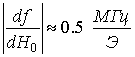 .
.
Выводы
В работе теоретически и экспериментально исследован эффект расталкивания резонансных частот магнитодинамических колебаний в намагниченных ферритовых резонаторах, которые имеют форму диска и прямоугольного параллелепипеда. Показано, что моделирование в программном продукте HFSS 13 хорошо описывает частотно-полевые зависимости и АЧХ для намагниченных ферритовых резонаторов размещенных как неоднородность в прямоугольном волноводе.
Выяснено, что преобладающей причиной начального расталкивания резонансных частот колебаний ферритового резонатора при отсутствии поля подмагничивания в условиях эксперимента [5] является влияние боковых стенок волновода. Полного совпадения теоретического расчета и экспериментальных данных не получено, поскольку в модели не учитывались механизм возникновения начального расталкивания резонансных частот связанный с наличием доменной структуры.
Экспериментально и путем
численных расчетов показано возможность минимизации начального расталкивания
резонансных частот ферритовых резонаторов. Это позволило увеличить модуль крутизны частотно-полевой зависимости резонансных частот магнитодинамических колебаний в
области малых магнитных полей (![]() ~100-200 Э) практически
вдвое: от 0.5 МГц/Э при наличии начального расталкивания резонансных частот до 1
МГц/Э при оптимальных размерах резонатора.
~100-200 Э) практически
вдвое: от 0.5 МГц/Э при наличии начального расталкивания резонансных частот до 1
МГц/Э при оптимальных размерах резонатора.
Литература
1. Subramanyam G. Challenges and opportunities for multi-functional oxide thin films for voltage tunable radio frequency/microwave components / G. Subramanyam, M. W. Cole, N. X. Sun, T. S. Kalkur, N. M. Sbrockey et al. // J. Appl. Phys. – 2013. – Vol. 114., Iss. 19. – P. 191301 (1-35).
2. Ozgur U. Microwave ferrites, part 2: passive components and electrical tuning. / U. Ozgur, Y. Alivov, H. Markoc // Journal of Material Science: Materials in Electronics. – 2009. - Vol. 20, Iss. 10 – P. 911-952.
3. Tatarenko A.S. Microwave magnetodielectric devices. / A.S. Tatarenko, M.I. Bichurin // Advances in Condensed Matter Physics, – 2012. – Vol. 2012. – P. 286562 (1-10).
4. Srinivasan G. Millimeter-wave magnetoelectric effect in bilayer of barium hexaferrite and zirconate titanate / G. Srinivasan, I. V. Zavislyak, A. S. Tatarenko // Appl. Phys. Lett. – 2006. – Vol. 89, Iss. 15. – P. 152508 (1-3).
5. Popov M. A Sub-THz dielectric resonance in single crystal yttrium iron garnet and magnetic field tuning of the modes / M. A. Popov, I. V. Zavislyak, G. Srinivasan // J. Appl. Phys. – 2011. – Vol. 110, Iss. 2. – P. 024112 (1-7).
6. Popov M. A. Sub-Terahertz Magnetic and Dielectric Excitations in Hexagonal Ferrites / M. A. Popov, I. V. Zavislyak, G. Srinivasan // IEEE Trans. on magnetics. – 2011. – Vol. 47, №. 2 – P. 289-294.
7. Мовчан Н. Н. Расщепление аксиально неоднородных мод в гиромагнитных и гироэлектрических резонаторах миллиметрового диапазона / Н. Н. Мовчан, И. В. Зависляк, М. А. Попов // Известия вузов. Радиоэлектроника. – 2012. – Т. 55, № 12 – С. 31-40.
8. Popov M. A. Magnetic field tunable 18-36 GHz dielectric bandpass filter / M. A. Popov, D. V. B. Murthy, I. V. Zavislyak, G. Srinivasan // Electronics letters. – 2012. – Vol. 48, No. 2. – P. 98-99.
9. Popov M. A. A magnetic field tunable yttrium iron garnet millimeter-wave dielectric phase shifter: theory and experiment / M. A. Popov, I. V. Zavislyak, G. Srinivasan // PIER C. – 2012. – Vol. 25 – P. 145-157.
10. Popov M. A Tunable magneto-dielectric resonator for W-band isolators / M. A. Popov, I. V. Zavislyak, G. Srinivasan // Electronics letters. – 2009. – Vol. 45, No. 24. – P. 1216-1218.
11. Schlomann E. Microwave behavior of partially magnetized ferrites / E. Schlomann // J. Appl. Phys. – 1970. – Vol. 41, No 1. – P. 204-214.
12. Ильинский А. С. Колебания и волны в электродинамических системах с потерями / А.С. Ильинский, Г.Я. Слепян. – М.: Изд-во МГУ, 1983. – 232 с.
13. Мандельштам Л. И. Лекции по теории колебаний / Л. И. Мандельштам; Под ред. С.М. Рытова. – М.: Наука, 1972. – 470 с.
14. Beleggia M. The equivalent ellipsoid of a magnetized body / M. Beleggia, M. De Graef, Y. T.Millev // J. Phys. D: Appl. Phys. –2006. – Vol. 39. – P. 891−899.
15. Ильченко М. Е. Диэлектрические резонаторы / М.Е. Ильченко, В. Ф. Взятышев, Л.Г. Гасанов и др.; Под ред. М. Е. Ильченко – М.: Радио и связь, 1989. – 328 с.