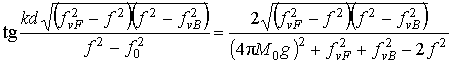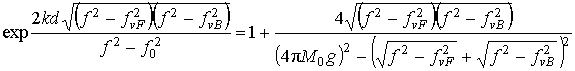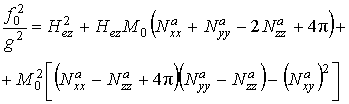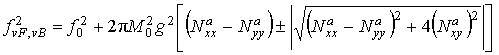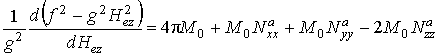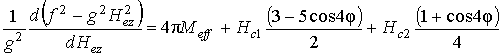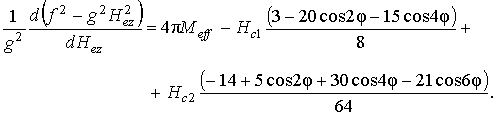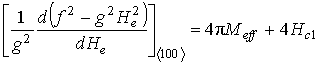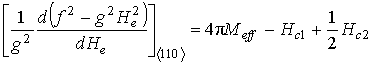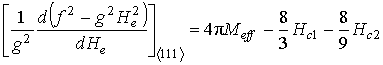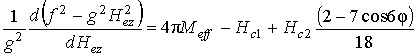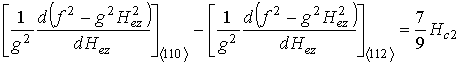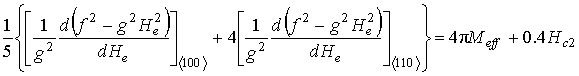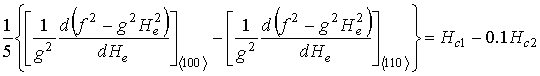УДК 538.975

ЧАСТОТНО-ПОЛЕВЫЕ ЗАВИСИМОСТИ В СПЕКТРЕ ПОВЕРХНОСТНОЙ МАГНИТОСТАТИЧЕСКОЙ ВОЛНЫ И ИХ ИСПОЛЬЗОВАНИЕ ДЛЯ ОПРЕДЕЛЕНИЯ МАГНИТНЫХ ПАРАМЕТРОВ ФЕРРИТОВЫХ ПЛЁНОК

 

В. В. Шагаев, Тун Тун Лин

Московский государственный технический университет им. Н.Э. Баумана, Калужский филиал

 

Статья получена 16 января 2015 г.

 

Аннотация. Выведено уравнение, характеризующее поверхностную магнитостатическую волну в плёнке с точки зрения зависимости частоты волны от напряжённости намагничивающего поля. Особенность уравнения состоит в том, что оно не зависит от волнового числа. Выполнен анализ частотно-полевого уравнения в плёнках кубических ферритов с ориентациями типа {100}, {110}, {111}. При этом были учтены первая и вторая константы кубической анизотропии феррита. На основе выведенного уравнения разработан метод измерения магнитных параметров плёнок. Приведены результаты экспериментальных исследований, в которых были определены температурные зависимости эффективной намагниченности и поля магнитной кристаллографической анизотропии в плёнке железоиттриевого граната.

Ключевые слова: магнитостатическая волна, ферриты, железоиттриевый гранат, магнитная анизотропия, намагниченность.

Abstract: The equation characterizing a magnetostatic surface wave in a film from a viewpoint of the wave frequency dependence on the magnetizing field strength is deduced. The peculiarity of the equation consists in the fact that it doesn't depend on wave number. The analysis of the equation of the frequency dependence on a field in films of the cubic ferrites with orientations of type {100}, {110}, {111} is executed. In this case the first and the second constants of cubic anisotropy of ferrite were taken into account. On the basis of the deduced equation the method of measurement of the films magnetic parameters is developed. Results of the experimental investigations in which the dependences of the effective magnetization and the magnetic crystallographic anisotropy field on temperature in a film of iron-yttrium garnet was defined are given.

Key words: magnetostatic wave, ferrites, yttrium iron garnet, magnetic anisotropy, magnetization.

 

Введение

Законы дисперсии магнитостатических волн (МСВ), распространяющихся в плёнках ферритов, определяют характеристики построенных на их основе приборов [1]. Наибольшее применение нашли плёнки кубических ферритов, выращиваемые на монокристаллических подложках. Такие плёнки обладают двумя видами магнитной анизотропии – кристаллографической и одноосной. На законы дисперсии влияют оба вида. К настоящему времени законы дисперсии МСВ в анизотропных плёнках достаточно подробно изучены как теоретически, так и экспериментально (см., например, [2–5]). При этом наиболее детально исследовано влияние первой константы магнитной кубической анизотропии, поскольку в широко используемых ферритах именно она имеет наибольшее значение. Вместе с тем учёт второй константы позволяет повысить точность проектирования спин-волновых устройств. Например известно, что в плёнках железоиттриевого граната (ЖИГ) с кристаллографической ориентацией типа {111} угловая зависимость частот поверхностной МСВ (ПМСВ) в равной степени определяется первой и второй константами [3]. Интерес к учёту в характеристиках МСВ второй константы может быть обусловлен и перспективой получения новых материалов со сравнимыми значениями первой и второй констант. Также имеется необходимость в развитии методов измерения констант магнитной анизотропии.

В настоящей работе рассмотрена зависимость частот ПМСВ от намагничивающего поля и изучено влияние на эту зависимость магнитной анизотропии. В частности из законов дисперсии МСВ можно рассчитать производную от квадрата частоты по напряжённости поля и выразить её через линейную комбинацию эффективных размагничивающих факторов анизотропии. При этом получающееся выражение будет зависеть от кристаллографической ориентации вектора намагниченности, что может быть использовано для определения материальных параметров ферритовых плёнок. В работе [6] были рассмотрены частотно-полевые зависимости, но только для отдельных кристаллографических направлений и с учётом только одной константы анизотропии. Цель данной работы состояла в том, чтобы обобщить ранее полученные результаты. Частотно-полевые соотношения были выведены в виде зависимостей от угла, определяющего ориентацию вектора намагниченности в плоскости плёнки, и при этом были учтены две константы анизотропии.

 1. Преобразование дисперсионного уравнения поверхностной магнитостатической волны в уравнение частотно-полевой зависимости

Дисперсионные уравнения МСВ в плёнке выводятся из уравнений Максвелла в магнитостатическом приближении и с электродинамическими граничными условиями и уравнения движения намагниченности без учёта обмена и потерь (уравнения Ландау-Лифшица). При этом магнитную анизотропию феррита можно учесть с помощью эффективных размагничивающих факторов [7]. В касательно намагниченной до насыщения анизотропной плёнке в случае, когда волновой вектор МСВ перпендикулярен вектору равновесной намагниченности ( и ,  – нормаль к плёнке), дисперсионные уравнения (ДУ) могут быть двух типов [5]:

                                 (1)

 

для объемных волн и

         (2)

   

для поверхностной (или смешанной при ) волны. Здесь  – частота МСВ;  – волновое число;  – толщина плёнки;  – намагниченность насыщения феррита;  – гиромагнитное отношение (для широко используемых ферритов  МГц/Э). Остальные параметры выражаются формулами:

                                                      (3)

              ,          (4)

где , , ,  – эффективные размагничивающие факторы анизотропии в системе координат с осями , , , причём, ось направлена вдоль вектора равновесной намагниченности (), а ось  – вдоль волнового вектора ();  – проекция вектора напряжённости внешнего намагничивающего поля  на вектор . Параметр  является длинноволновой граничной частотой спектра МСВ и совпадает с частотой однородного ферромагнитного резонанса.  и  – соответственно коротковолновые граничные частоты многомодовых спектров прямых объёмных () и обратных объёмных () волн. Дисперсионная зависимость (2) описывает спектр МСВ в частотном интервале

                                                      ,                                                  (5)

                           

 

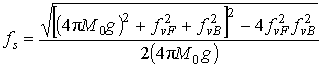
Причём, дисперсионная зависимость основной моды прямой объёмной волны плавно переходит в дисперсионную зависимость поверхностной волны на частоте  и при значении нормированного волнового числа.

                            .

 

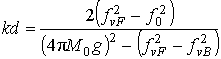Графики, изображённые на рис. 1, демонстрируют структуру спектра МСВ. Расчёт был выполнен с помощью уравнений (1), (2).

 

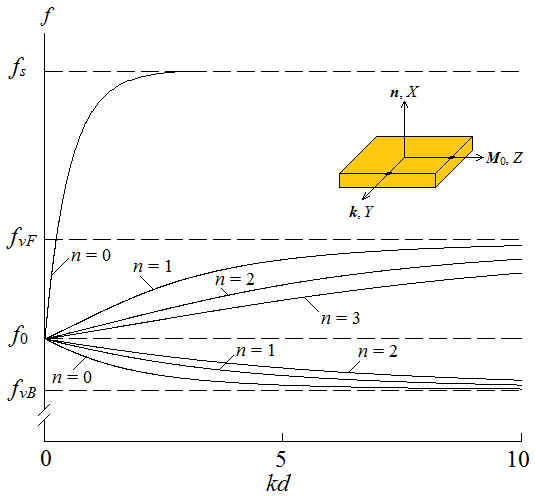
Рис. 1. Дисперсионные зависимости МСВ в касательно намагниченной анизотропной плёнке;
параметром «n» обозначены номера нескольких изображённых объемных мод;
в расчётах полагалось: ; ;

 

Поставленная задача – вывод зависимости  из ДУ (1), (2) – на первый взгляд кажется трудно разрешимой, поскольку из ДУ нельзя получить явное выражение для . Вместе с тем уравнения (1) и (2) обладают следующей особенностью: после подстановки в них выражений (3), (4) параметры f и  образуют комбинацию

                    .

Если полагать, что в ДУ от значения  может зависеть только значение , а значения остальных параметров не меняются, то функция  должна быть константой. Тогда будет выполняться соотношение: . Из него получим:

                    .                (6)

 

Данное уравнение может быть использовано для определения магнитных параметров ферритовых плёнок. Для этого необходимо получить экспериментальную зависимость f(H_e) при любом фиксированном значении волнового числа и по ней рассчитать левую часть уравнения. При этом в правую часть нужно подставить выражение, рассчитанное на основе выбранной модели плёнки. В результате получится уравнение с известной левой частью и с набором материальных параметров в правой части. Правая часть будет зависеть от угла, задающего кристаллографическую ориентацию . Используя различные значения этого угла, можно составить систему уравнений, достаточную для расчёта всех входящих в модель параметров. В настоящей работе уравнение (6) было применено к плёнкам кубических ферритов.

 2. Модель ферритовой плёнки

Расчёты эффективных размагничивающих факторов были выполнены для плёнки с кубической и нормальной одноосной магнитной анизотропией. Полагалось, что кристаллографическая ось типа  расположена в плоскости плёнки (рис.2). При этом кристаллографическая ориентация плёнки задана углом наклона к плёнке оси типа , перпендикулярной к упомянутой оси  (угол ). Тогда значениям угла 0,  и  будут соответствовать кристаллографические ориентации плёнки типа {110}, {111} и {100}. В дальнейшем изложении рассмотрены именно эти ориентации.

 

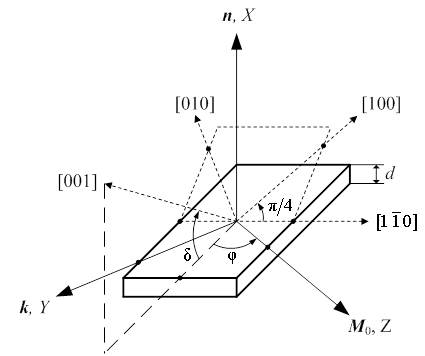
Рис. 2. Исследованная модель плёнки из кубически анизотропного феррита

 

Основой для расчёта эффективных размагничивающих факторов является плотность энергии магнитной анизотропии. Было использовано следующее выражение:

                          .                      (7)

Первое и второе слагаемые описывают кубическую анизотропию [7]. Причём,  – косинусы углов между вектором намагниченности и тремя кристаллографическими осями симметрии четвёртого порядка, образующими прямоугольную систему координат. Третье слагаемое в (7) учитывает одноосную анизотропию, присущую плёнкам, выращиваемым на подложках.

Энергию кубической анизотропии удобно выразить через проекции вектора намагниченности на оси , , . Сначала нужно выразить соответствующие слагаемые в (7) через проекции вектора намагниченности на ортогональные оси , , . При этом энергия кубической анизотропии с точностью до независящей от ориентации намагниченности константы примет вид:

                .            (8)

 

Для перехода к проекциям на оси , ,  необходимо сделать подстановку:

                                                    ,                                                (9)

где индексы принимают значения: ; . Матрица косинусов углов между осями рассматриваемых систем координат  может быть рассчитана с помощью рис. 2 и имеет вид ( – строка,  – столбец):

          .    (10)

В результате подстановок выражений (9) и (10) в формулу (8) энергия  будет преобразована в функцию от проекций , , . Далее необходимо вычислить производные  и в линейном приближении по малым компонентам ,  преобразовать их к виду:

            .

 

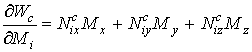Коэффициенты при проекциях вектора намагниченности будут искомыми эффективными размагничивающими факторами кубической анизотропии.

Энергию одноосной нормальной анизотропии в (7) можно представить в виде ряда [7]:

            ,

где  – угол между вектором намагниченности и нормалью к плёнке. Поскольку в рассматриваемой модели , то при малом отклонении вектора намагниченности от равновесного положения изменение  будет определяться компонентой  и при этом . Тогда единственным отличным от нуля эффективным размагничивающим фактором одноосной анизотропии будет .

 3. Частотно-полевые уравнения в плёнках с кристаллографическими ориентациями типа {100}, {110} и {111}

3.1. Плёнки с ориентацией типа .

Значение  соответствует именно такой плёнке. Расчёт по описанной в предыдущем разделе схеме приводит следующим выражениям:

            ; ; .

 

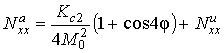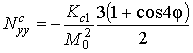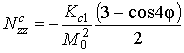Уравнение (6) после подстановки выражений примет вид:

             ,       (11)

где  – эффективная намагниченность;  и  – компоненты поля кубической магнитной анизотропии. Кроме того, при намагничивании вдоль касательных осей типа  и  проекция  будет совпадать с полной напряженностью намагничивающего поля. То есть для значений  и  в производной можно сделать замену . Такая замена обусловлена тем, что преобразования симметрии кристаллической решётки не должны менять ориентацию вектора намагниченности в намагниченной до насыщения плёнке. В рассматриваемой геометрии такое возможно только, когда .

3.2. Плёнки с ориентацией типа .

В данном случае , и эффективные размагничивающие факторы выражаются формулами:

            ,

            ,

            .

 

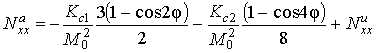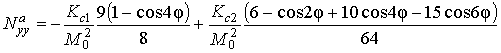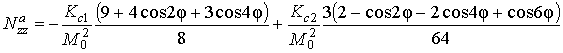Частотно-полевое уравнение (6) после всех подстановок и алгебраических преобразований примет вид:

                       (12)

В плоскости плёнок с ориентацией типа  расположены кристаллографические оси симметрии типа , , , и сама плоскость  является плоскостью симметрии кристалла. Анализ, основанный на преобразованиях симметрии, показывает, что для всех трёх типов осей можно полагать . Каждый из косинусов в правой части уравнения (12) может быть выражен через . При этом направлениям вдоль осей типа  соответствует значение , вдоль  – , вдоль  – . Для этих значений получаются следующие частотно-полевые уравнения:

                                ,                          (13)

                           ,                    (14)

                         .                   (15)

 

Левые части уравнений могут быть определены из экспериментальных зависимостей , полученных при любом значении волнового числа ПМСВ. После этого параметры , ,  могут быть рассчитаны из системы линейных уравнений (13), (14), (15). Таким образом, в плёнках с ориентацией типа  имеется возможность определить три магнитных параметра, входящих в дисперсионные уравнения МСВ, не делая при этом пересчёта значений  в .

3.3. Плёнки с ориентацией типа .

В компоненты матрицы (10) нужно подставить значения  и . Тогда расчёт даёт:

                            ,

                            ,

                            .

 

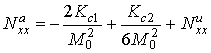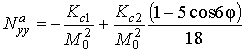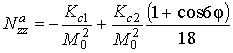Уравнение (6) с этими выражениями можно преобразовать к виду:

                      .                (16)

 

Интересно отметить, что угловая зависимость правой части связана только с полем . Это даёт возможность рассчитать  по двум значениям производной. Например, можно определить производную для кристаллографических направлений типа  и , расположенных в плоскости плёнки. В первом случае , во втором – . Тогда из уравнения (16) получается расчётное соотношение:

                  .           (17)

 

В рассматриваемом типе плёнок их плоскость уже не будет плоскостью симметрии. Поэтому вектор  не будет параллелен вектору , и в производных нельзя заменить  на . На практике же контролируется ориентация и значение вектора . Однако, для ферритов со слабой анизотропией и помещенных в сильное намагничивающее поле погрешность, обусловленная отличием  от , может быть несущественной.

 4. Методика эксперимента

Для экспериментов была использована плёнка ЖИГ с кристаллографической ориентацией типа . Возбуждение и приём ПМСВ осуществлялись с помощью микрополоскового модуля, конструкция которого изображена на рис. 3.

 

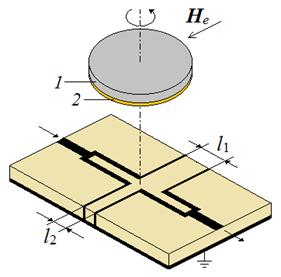
Рис. 3. Интерферометр спиновых волн; 1 – подложка из гадолиний галлиевого граната; 2 – плёнка ЖИГ

 

Исследуемый образец прижимался к модулю, после чего измерялась его амплитудно-частотная характеристика (АЧХ). Выбор кристаллографического направления намагничивания реализовывался поворотом образца. Примеры АЧХ изображены на рис. 4.

Рис. 4. Спектры ПМСВ в плёнке ЖИГ с кристаллографической ориентацией типа  и толщиной ,
измеренные при  и при разных температурах

 

Волны, распространяющиеся между двумя парами полосков (антенн), при сложении имеют разность фаз . В максимумах АЧХ разность фаз равна , где  – номер максимума. В минимумах – . Полоски имели ширину  и разность . Таким образом, каждому экстремуму АЧХ в соответствии с его номером можно сопоставить определённое значение волнового числа . Зависимости  измерялись для частот, расположенных в максимумах АЧХ.

Необходимую для составления частотно-полевого уравнения производную можно получить из зависимости разности  от . Примеры таких зависимостей приведены на рис. 5.

 

Рис. 5. Экспериментальные частотно-полевые зависимости, полученные в спектре ПМСВ

 

Ориентация поля  выставлялась по минимуму угловой зависимости спектра ПМСВ, а ориентация  – по максимуму. Графики на рис. 5 хорошо аппроксимируются линейными зависимостями с одинаковыми наклонами (производными) для разных значений . Вместе с тем для разных ориентаций  наклоны имели видимые отличия. Данные особенности находятся в соответствии с частотно-полевым уравнением (6).

 5. Температурные зависимости магнитных параметров

Уравнение (11) в условиях, когда  и , и соответственно  и , приводит к системе из двух уравнений:

                  ,

                  .

 

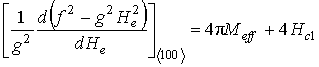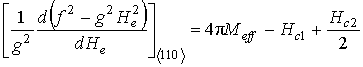Комбинации уравнений приводят к следующим соотношениям:

                  ,     (18)

                  .             (19)

 

Производные в левых частях были определены из экспериментальных исследований при разных температурах. В результате были получены зависимости, изображённые на рис. 6.

 

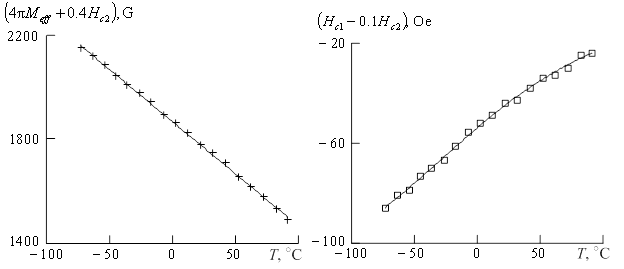
Рис. 6. Зависимости от температуры эффективной намагниченности и поля кубической анизотропии плёнки ЖИГ с поправками,
учитывающими вторую константу кубической анизотропии

 

В ЖИГ выполнятся неравенство . Так, при  [3]: , . К тому же коэффициенты, с которыми  входит в соотношения (18), (19), дополнительно ослабляют влияние поля  на эти соотношения. Для практических целей зависимости, приведённые на рис. 6, можно использовать без поправок с полем  и при этом они хорошо согласуется с зависимостями  и , полученными другими экспериментальными методами [8, 9].

 Выводы

Полученные результаты могут быть использованы при разработке и совершенствовании материалов спин-волновой электроники. Предложенный в статье метод определения ключевых параметров ферритовых плёнок основан на выявленной закономерности в спектре ПМСВ и поэтому наилучшим образом подходит для данной категории материалов. Выведены соотношения, на основе которых в плёнках кубических ферритов могут быть определены три параметра – , , .

Использование метода было продемонстрировано на плёнке ЖИГ. Экспериментальный модуль позволял фиксировать значение волнового числа и отслеживать соответствующую ему частоту при изменении условий распространения волны. При этом волновое число не входит в расчётные выражения, и его фиксируемые значения можно было не определять. Это обстоятельство существенно упрощает эксперимент. Были получены температурные зависимости намагниченности насыщения и поля кубической магнитной анизотропии, которые согласуются с данными из других источников.

 

Литература

1. Вашковский А.В., Стальмахов В.С., Шараевский Ю.Г. Магнитостатические волны в электронике СВЧ. – Саратов: Изд.-во СГУ, 1993. – 316 с.

2. Берегов А.С. Магнитостатические волны в структуре с произвольно намагниченной пленкой кубического ферромагнетика // Изв. ВУЗов. Сер. Радиоэлектроника. – 1984. – Т. 27, № 10. – С. 9-16.

3. Чивилева О.А., Гуревич А.Г., Эмирян Л.М. Влияние кубической анизотропии на спектр поверхностных спиновых волн в плёнке с плоскостью {111} // ФТТ. – 1987. – Т. 29, № 1. – С. 110-115.

4. Шагаев В.В. О влиянии магнитной кристаллографической анизотропии на температурные характеристики магнитостатических волн в ферромагнитных плёнках // ФТТ. – 2003. – Т.45, № 12. – С. 2215-2221.

5. Шагаев В.В. Метод расчета характеристик поверхностных магнитостатических волн в анизотропных ферромагнитных плёнках // ЖТФ. 2004. T.74. Вып. 10. С. 108-112.

6. Шагаев В.В. Зависимость частот магнитостатических волн от напряжённости поля подмагничивания в ферритовых плёнках // ФТТ. – 1998. – Т.40, № 11. – С. 2089-2092.

7. Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. – М.: Наука, 1994, 464 с.

8. Hansen P., Röschmann P. and Tolksdorf W. Sutaration magnetization of gallium-substituted yttrium iron garnet // J. Appl. Phys. – 1974. – Vol. 45, N 6. – P. 2728-2732.

9. Hansen P. Anisotropy and magnetostriction of gallium-substituted yttrium iron garnet // J. Appl. Phys. – 1974. – Vol. 45, N 8. – P. 3638-3642.