УДК: 519.61, 004.02, 004.67
ТЕОРЕМЫ ОБ УМЕНЬШЕНИИ РАЗМЕРНОСТИ ПРОСТРАНСТВА ПРИ КОРРЕЛЯЦИИ И СВЁРТКЕ
А. Ю. Гришенцев
Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики
Статья получена 21 января 2015 г.
Аннотация. В работе сформулированы и доказаны теоремы об уменьшении размерности пространства при корреляции и свёртке n-мерных последовательностей. В качестве иллюстрации рассмотрены некоторые примеры. Данные теоремы могут найти широкое применение в задачах цифровой обработки сигналов, широкополосной радиосвязи, исследованиях уединённых волн (солитонов) и других прикладных и теоретических естественнонаучных областях знаний.
Ключевые слова: корреляция, свёртка, многомерные сигналы, оптимизация вычислений, цифровая обработка, широкополосные сигналы.
Abstract. In this paper we formulate and prove theorems about reducing the space dimension and the correlation with the convolution of n-dimensional sequences. As an illustration, we consider some examples. These theorems can be widely used in the problems of digital signal processing, broadband radio, studies solitary waves (solitons) and other applied and theoretical natural science fields.
Keywords: correlation, convolution, multi-dimensional signals, the optimization of computing, digital, broadband signals.
Введение
Формализация, обобщение и общая систематизация один из ключевых вопросов эффективного использования математического аппарата. Особого внимания требует формализация методов вычислительной математики [1,2], цифровой обработки сигналов [3,4,5], широкополосных систем связи [6] и ряда других смежных дисциплин, это связано с тем, что прикладным разработчикам нужен готовый к использованию математический инструментарий [7,8], позволяющий реализовать эффективные аппаратные, программные и смешанные решения. Наилучший набор инструментария для практического разработчика это готовые системы, выполненные в виде микросхем или целых схемотехнических модулей, программных библиотек, причём имеющих высокий уровень многокритериальной оптимизации и достаточное множество опций конфигурации. Построение таких систем возможно только на основе развитого математического аппарата и междисциплинарного подхода при решении вопросов проектирования [9,10].
Данная работа посвящена формулировке и доказательству теорем об уменьшении размерности пространства при корреляции и свёртке последовательностей. Реализация рассмотренных теорем может быть выполнена доступными вычислительными средствами, способствуя их более эффективному использованию.
Теоремы об уменьшении размерности пространства при корреляции и свёртке
Введём следующие обозначения, n-мерное пространство Rn, существования произвольной последовательности a[Rn] есть пространство заданное измерениями {X0,X1, ..., Xn-1} где n – есть число измерений пространства Rn, каждое измерение последовательности определяется отсчётами Xk={xk0,xk1,…} для k=0...n–1 каждому отсчёту соответствует пространство Rn–Xk. Для двух последовательностей f[Rn] и h[Rn] заданных в пространстве Rn, операцию свёртка будем обозначать f[Rn]*h[Rn], операцию корреляция – f[Rn]•h[Rn]. Например, если отдельно взятый элемент последовательности a[Rn] есть число, то для нольмерного (n=0) пространства R0 последовательность a[R0] будет соответствовать скаляру, для одномерного (n=1) пространства R1 – вектору, для двумерного (n=2) пространства R2 – матрице. Следует отметить, что в более общем случае отдельно взятый элемент последовательности a[Rn] может быть тензором, следовательно, последовательность a[Rn] будет тензорным полем. В рамках данной работы термин последовательность будет эквивалентен термину цифровой сигнал или дискретный сигнал.
Теорема 1. Пусть в пространстве Rn заданы последовательности f[Rn] и h[Rn], выберем
одно произвольное измерение Xk из Rn, тогда результат операции свёртка y[Rn]= f[Rn]*h[Rn], с
последующим суммированием по Xk есть
эквивалентен предварительному
суммированию 
и 
с последующей свёрткой y[Rn–Xk]= f[Rn–Xk]*h[Rn–Xk].
Доказательство 1.
Для каждой последовательности f[Rn] и h[Rn] определённой в пространстве Rn, задана соответствующая размерность {Xf0, Xf1,
..., Xfn–1} и {Xh0, Xh1,
..., Xhn–1} в
соответствии с множеством измерений {X0, X1, ..., Xn–1}.
Выберем и зафиксируем значения всех кроме одного отсчётов is (s≠k) и будем пробегать лишь один произвольный отсчёт ik (ik=0…
Xhk+Xfk–2)
для произвольного измерения Xk,
произведём свёртку, т.е. получим множество слагаемых для последующего
нахождения одного из элементов последовательности , запишем выражение в виде:
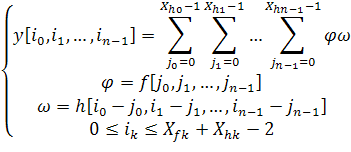
Затем вычислим сумму полученной последовательности y[i0, i1,…, in–1]
по отсчёту ik, в соответствии с
выражением: . В результате получим сумму комбинаторных
сочетаний без повторений всевозможных произведений 
с учётом изменения лишь одного
произвольного отсчёта ik.
Выполним действия иначе. Выберем и зафиксируем значения всех
кроме одного отсчётов is (s≠k) и будем пробегать лишь один произвольный отсчёт ik для произвольного
измерения Xk, вычислим суммы
понижающие размерность последовательностей и , затем выполним свёртку y[Rn–Xk]=f[Rn–Xk]*h[Rn–Xk], в результате получим сумму комбинаторных
сочетаний всевозможных произведений с учётом изменения лишь одного
произвольного отсчёта ik. Таким
образом, результаты для выбранных и зафиксированных значений всех is (s≠k) отсчётов,
кроме одного ik (ik=0…Xhk+Xfk–2), для произвольного измерения Xk, полученные двумя различными способами
совпадают.
Применяя приведённые выше рассуждения последовательно ко
всем отсчётам is (s≠k) последовательно
присваивая им все возможные значения, фиксируя и затем, пробегая лишь один отсчёт
ik (ik=0…Xhk+Xfk–2)
для измерения Xk, в соответствии с
приведёнными выше рассуждениями получим, что элементы y[Rn–Xk]
полученные свёрткой y[Rn]=f[Rn]*h[Rn], с
последующим суммированием по Xk т.е. , эквивалентны элементам y[Rn–Xk] полученным предварительным суммированием и с последующей свёрткой y[Rn–Xk]=f[Rn–Xk]*h[Rn–Xk], что и требовалось доказать.
Теорема 2. Пусть в пространстве Rn заданы последовательности f[Rn] и h[Rn], выберем
одно произвольное измерение Xk из Rn, тогда результат операции корреляция y[Rn]= f[Rn]•h[Rn], с
последующим суммированием по Xk есть
эквивалентен предварительному
суммированию и с последующей корреляцией y[Rn–Xk]= f[Rn–Xk]•h[Rn–Xk].
Доказательство 2.
Рассуждения для доказательства теоремы 2, аналогичны доказательству
1. Для каждой последовательности f[Rn] и h[Rn] определённой в пространстве Rn, задана соответствующая размерность {Xf0, Xf1,
..., Xfn–1} и {Xh0, Xh1,
..., Xhn–1} в
соответствии с множеством измерений {X0, X1, ..., Xn–1}.
Выберем и зафиксируем значения всех кроме одного отсчётов is (s≠k) и будем пробегать лишь один произвольный отсчёт ik (ik=0…
Xhk+Xfk–2)
для произвольного измерения Xk,
произведём корреляцию, т.е. получим множество слагаемых для последующего
нахождения одного из элементов последовательности , запишем выражение в виде:
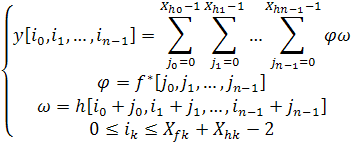
где f*[Rn], есть последовательность комплексно сопряженная к f[Rn], если последовательности образованны только вещественными числами, то сопряжение не требуется.
Затем вычислим сумму полученной последовательности y[i0, i1,…, in–1]
по отсчёту ik, в соответствии с
выражением: . В результате получим сумму комбинаторных
сочетаний без повторений всевозможных произведений 
с учётом изменения лишь одного
произвольного отсчёта ik.
Выполним действия иначе. Выберем и зафиксируем значения всех
кроме одного отсчётов is (s≠k) и будем пробегать лишь один произвольный отсчёт ik для произвольного
измерения Xk, вычислим суммы
понижающие размерность последовательностей и , затем выполним корреляцию y[Rn–Xk]=f[Rn–Xk]•h[Rn–Xk], в результате получим сумму комбинаторных
сочетаний всевозможных произведений с учётом изменения лишь одного
произвольного отсчёта ik. Таким
образом, результаты для выбранных и зафиксированных значений всех is (s≠k) отсчётов,
кроме одного ik (ik=0…Xhk+Xfk–2), для произвольного измерения Xk, полученные двумя различными способами
совпадают.
Применяя приведённые выше
рассуждения последовательно ко всем отсчётам is (s≠k) последовательно присваивая им все возможные значения,
фиксируя и затем, пробегая лишь один отсчёт ik для измерения Xk,
в соответствии с приведёнными выше рассуждениями получим, что элементы y[Rn–Xk] полученные корреляцией y[Rn]=f[Rn]•h[Rn], с
последующим суммированием по Xk т.е. , эквивалентны элементам y[Rn–Xk] полученным предварительным суммированием и с последующей корреляцией y[Rn–Xk]=f[Rn–Xk]•h[Rn–Xk], что и требовалось доказать.
Некоторые частные случаи и примеры использования теорем
Рассмотрим частные случаи применения теорем.
Пример 1. Свёртка двух векторов. Заданы два вектора X=(x0, x1, x2, x3, x4) и H=(h0, h1, h2), выполнить свёртку в соответствии с теоремой 1. В соответствии с выражением:
вычислим свёртку векторов X и H получим Y=H*X=(h0∙x0, h0∙x1+h1∙x0, h0∙x2+h1∙x1+h2∙x0, h0∙x3+h1∙x2+h2∙x1, h0∙x4+h1∙x3+h2∙x2, h1∙x4+h2∙x3, h2∙x4), затем вычислим поэлементную сумму вектора Y, получим ΣY=(h0∙x0+h0∙x1+h1∙x0+h0∙x2+h1∙x1+h2∙x0+h0∙x3+h1∙x2+h2∙x1+h0∙x4+h1∙x3+h2∙x2+h1∙x4+h2∙x3+h2∙x4) в результате получим сумму комбинаторных сочетаний без повторений всевозможных произведений элементов векторов X и H. Теперь, в соответствии с теоремой 1, получим указанный результат с помощью вычисления поэлементной суммы для векторов X и H, т.е. ΣX=(x0+x1+x2+x3+x4) и ΣH=(h0+h1+h2) с последующей свёрткой, т.е. перемножением скаляров (x0+x1+x2+x3+x4)∙(h0+h1+h2)=(h0∙x0+h0∙x1+h1∙x0+h0∙x2+h1∙x1+h2∙x0+h0∙x3+h1∙x2+h2∙x1+h0∙x4+h1∙x3+h2∙x2+h1∙x4+h2∙x3+h2∙x4)=ΣY, очевидно что результаты совпадают. Следует отметить, что если считать умножение или сложение за одну операцию, то для получения одинакового результата свёртка с последующим суммированием потребовала 29 операций, а суммирование с последующей свёрткой 7.
Пример 2. Выполнить корреляцию двух матриц X и H преобразовать результат в вектор:
.
Затем рассчитаем сумму матрицы Y по строкам и получим вектор (12, 14, 22, 12). Теперь в соответствии с теоремой 2 выполним следующую последовательность действий: рассчитаем построчную сумму матриц X и H, получим векторы (2, 1, 3) и (4, 6) соответственно, затем выполним корреляцию полученных векторов (2, 1, 3)•(4, 6)= (12, 14, 22, 12). Возможно, выполнить аналогичные операции для сумм по столбцам матрицы Y даст результат
,
а для свертки суммы по столбцам матриц X и H соответственно
.
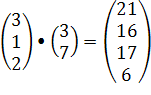Очевидно, что результаты совпадают. При расчёте корреляции с последующим суммированием число операций составляет 66, при суммировании с последующей корреляцией – 9.
Пример 3. Широкополосный сигнал существует в пространстве определяемым частотой и временем (ω, t), при этом ансамбль бинарных сигнатур, определяющий широкополосный сигнал, образован матрицей Адамара и имеет вид:
,
положим, что строки имеют постоянную частоту ω, автокорреляция матрицы H•H будет иметь вид:
,
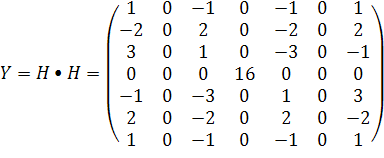сумма матрицы Y по строкам: (4, 0, -4, 16, -4, 0, 4). Применив теорему 2, рассчитаем сумму матрицы H по строкам с последующий автокорреляцией полученных векторов: (2, -2, 2, 2) •(2, -2, 2, 2)= (4, 0, -4, 16, -4, 0, 4). Полученные результаты совпадают.
Обсуждение, выводы
В работе сформулированы и доказаны теоремы об уменьшении размерности пространства при корреляции и свёртке. Применение данных теорем для решения практических задач может способствовать существенному сокращению объёма вычислений, особые перспективы использования в задачах распознавания образов, например, в системах широкополосной связи.
Литература
1. Гантмахер Ф. Р. Теория матриц. – М.: из-во «Наука», 1967. – 576 с.: ил.
2. Новиков С. П., Тайманов И. А. Современные геометрические структуры и поля. – М.: МЦНМО, 2005. – 584 с.: ил.
3. Оппенгейм А., Шафер Р. Цифровая обработка сигналов. 2-е издание, испр. М.: Техносфера, 2009. – 856 с.: ил.
4. Гришенцев А. Ю., Коробейников А. Г. Декомпозиция n-мерных цифровых сигналов по базису прямоугольных всплесков. // Научно-технический вестник информационных технологий, механики и оптики – 2012. – № 4 (80). – С. 75-79.
5. Гришенцев А. Ю. Эффективное сжатие изображений на базе дифференциального анализа. // Журнал радиоэлектроники: электронный журнал. 2012. №11. URL: http://jre.cplire.ru/jre/nov12/1/text.pdf
6. Ипатов В. Широкополосные системы и кодовое разделение сигналов. Принципы и приложения. М.: Техносфера, 2007. – 488 с.: ил.
7. Брей Б. Микропроцессоры Intel: 8086/8088, 80186/80188, 80286, 80386, 80486, Pentium, Pentium Pro Processor, Pentium II, Pentium III, Pentium 4. Архитектура, программирование и интерфейсы. Шестое издание: пер. с англ. – СПб.: БХВ-Петербург, 2005. – 1328 с.: ил.
8. Редькин П. П. Микроконтроллеры Atmel архитектура AVR32 семейства AT32UC3. Руководство пользователя. М.: Техносфера, 2010. – 784 с.: ил.
9. Герасимов И. В., Сафьянников Н. М., Якимовский Д. О. Сложно-функциональные блоки смешанных систем на кристалле: автоматизация функционального проектирования: Монография / под ред. И. В. Герасимова. – СПб.: Изд-во «ЭЛМОР», 2012. – 237 с.: ил.
10. Анисимов В. И. Топологический расчет электронных схем. – Л.: Энергия, 1977 . – 240 с.