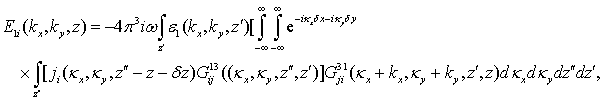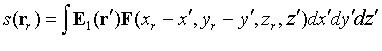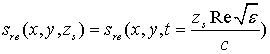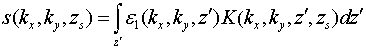УДК 621.371+537.87
О БЛИЖНЕПОЛЬНОЙ СВЧ ДИАГНОСТИКЕ НЕОДНОРОДНОСТЕЙ В СИЛЬНОПОГЛОЩАЮЩИХ СРЕДАХ 1
К. П. Гайкович 1,2, Е. С. Максимович 3
1 Институт физики микроструктур Российской академии наук, г. Нижний Новгород
2 Нижегородский государственный университет им. Н.И. Лобачевского
3 Институт прикладной физики Национальной академии наук
Беларуси, г. Минск
Статья получена 23 декабря 2014 г.
Аннотация. В работе анализируются возможности многочастотной СВЧ диагностики диэлектрических неоднородностей в средах с сильным поглощением. Исследуемый подход использует опыт создания аналогичной системы зондирования сред с относительно слабым поглощением. Алгоритмы анализа данных этой системы для томографии и голографии подповерхностных неоднородностей, основанные на решении обратной задачи ближнепольного рассеяния, модифицируются в применении к новым параметрам системы и диэлектрическим параметрам сильнопоглощающих сред и исследуются в численном моделировании.
Ключевые слова: томография, голография, диэлектрик, неоднородные среды, рассеяние СВЧ излучения.
Abstract: In this paper, possibilities of multifrequency microwave diagnostics of dielectric inhomogeneities in media with a strong absorption are studied. At that, experience with a similar system that has been worked for diagnostics of low-absorbing media is in use. Algorithms of tomography and holography based on the solving the inverse problem of near-field scattering that have been applied in data processing are modified in application to new parameters of strongly absorbing media and studied in the numerical simulation.
Key words: tomography, holography, dielectric, inhomogeneous media, scattering of microwave radiation.
1. Введение
Задача томографии, то есть получения трехмерного (3D) распределения диэлектрической проницаемости в среде с подповерхностной неоднородностью, в данном случае состоит в решении обратной задачи рассеяния на основе использования данных многочастотных СВЧ измерений поля, рассеянного диэлектрическими объектами на глубине порядка размеров ближнего поля для наибольшей длины волны частотного диапазона зондирующего сигнала. Ближнепольные измерения привлекают возможностью выхода за релеевское ограничение разрешающей способности, что является единственным способом, когда переход к более коротковолновому диапазону невозможен из-за возрастания ослабления в среде, например такой, как биологические ткани.
В данной работе
развивается подход к ближнепольной сканирующей томографии [1], основанный на
схеме измерений, предложенной в [2], в которой измерения в двумерной области
над неоднородностью выполняются с помощью жестко связанной системы
источник-приемник. Глубинную чувствительность обеспечивают измерения в зависимости
от третьего параметра, такого, как частота сигнала, размер апертуры приемной
антенны или высота уровня сканирования. Эта схема приводит 3D
уравнение в борновском приближении к уравнению типа свертки, редуцируемому к
одномерному интегральному уравнению, которое должно решаться для каждой пары
волновых чисел двумерного поперечного спектра. Более того, этот подход
позволяет получать и некоторую коррекцию к решению в борновском приближении.
Поперечные спектры функций Грина, образующие ядро решаемого уравнения были
получены в [2] в явном виде. Там же был апробирован и метод решения таких
уравнений Фредгольма 1-го рода для комплекснозначных функций в пространстве
Соболева 
, основанный на
принципе обобщенной невязки.
Следует отметить, что для сплошных, внутренне однородных, объектов, которые на практике встречаются значительно чаще распределенных неоднородностей, исчерпывающей характеристикой является геометрическая форма поверхности, однако ее получение (задача компьютерной голографии) на основе результатов решения описанной более общей задачи томографии не является тривиальной задачей. Математически последовательный подход к задаче голографии таких объектов и первые результаты также были получены в [3]. До некоторой степени аналогичные подходы в настоящее время развиваются также с целью получения радиоголографических изображений поверхности металлических неоднородностей [4].
Описанные подходы были реализованы в эксперименте для подповерхностной СВЧ томографии неоднородностей в грунте [3], где были получены хорошие результаты томографии для распределенных и сплошных тестовых неоднородностей в средах с относительно небольшими значениями диэлектрических параметров. Среди возможных применений этой методики весьма важными представляются медико-биологические приложения, но непосредственное применение описанной в [3] системы для этой цели оказывается невозможным. Причиной является тот факт, что диэлектрические параметры живых тканей имеют существенно большие значения, что приводит к сильному поглощению волн в частотном диапазоне системы [3] (1,7 – 7 ГГц) и сильному отражению от поверхности. В данной работе на основе численного моделирования рассматриваются возможные изменения ее параметров, которые позволили бы применить развитые алгоритмы для медико-биологической диагностики.
2. Теория
Если в среде с комплексной
диэлектрической проницаемостью 
имеется
рассеивающая трехмерная неоднородность 
, так
что 
, то комплексные амплитуды электрического поля
на частоте 
могут быть представлены как сумма
зондирующего и рассеянного полей 
. Для предлагаемой
схемы измерений (см. на рис.1) с фиксированным вектором 
,
определяющим сдвиг между приемной и передающей антеннами, поперечный спектр
рассеянного поля (двумерное фурье-преобразования по x и y) в
борновском приближении может быть представлен как интеграл от глубинного
профиля поперечного спектра неоднородностей в виде [2]:
где 
- компоненты соответствующих
функций Грина в k-пространстве для волн, распространяющихся из среды 1 в
среду 2 и обратно, 
- поперечный спектр
распределения тока источника зондирующего сигнала.
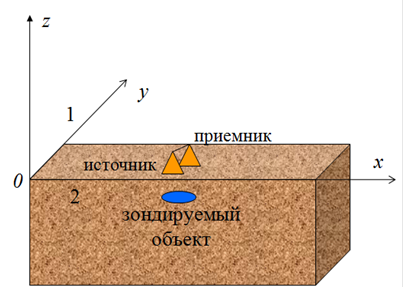
Рис.1. Схема измерений.
Вариации принимаемого
сигнала s1, связанные с рассеянным на подповерхностной
неоднородности полем, определяются сверткой по поперечным координатам
передаточной функции приемника F и рассеянного поля 
.
где положение приемника
определяется вектором 
. Это позволяет получить
одномерное интегральное уравнение, связывающее поперечный спектр вариаций
сигнала с глубинным профилем поперечного спектра неоднородностей
диэлектрической проницаемости:
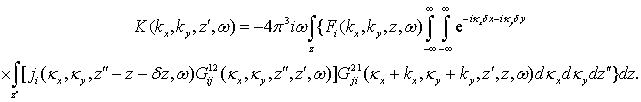
Интегральное уравнение Фредгольма 1-го рода (3) должно решаться для каждой пары спектральных компонент. Искомое трехмерное распределение (результат томографии) получается путем двумерного обратного фурье-преобразования полученного спектра. Исходными данными для анализа является двумерное распределение вариаций сигнала у поверхности среды над неоднородностью, измеренное на ряде частот. В [2] было показано, что в возможна и коррекция за пределами борновского приближения, для которой нужно внести соответствующие поправки в левую часть (3) или использовать для калибровки тестовые образцы со сравнимыми диэлектрическими параметрами.
Зависимость масштаба затухания сигнала в среде от частоты определяет глубинную чувствительность метода. Этот масштаб определяется как ближнепольными компонентами поперечного спектра рассеянного поля, так и поглощением в среде. При решении задачи с учетом ближнего поля нет принципиальных теоретических ограничений на разрешающую способность метода, однако, учитывая экспоненциальное затухание ближнепольных компонент и ненулевую погрешность измерений, такие ограничения неизбежно существуют, и разрешающая способность за пределами ближней зоны быстро стремится к релеевскому пределу.
Решение уравнения (3) было использовано в наших первых исследованиях метода томографии по экспериментальным данным [3]. Результаты показали, что наиболее серьезной проблемой метода являлся высокий уровень зашумленности данных поверхностным рассеянием, причем даже мелкомасштабные неоднородности вблизи антенны при многократном рассеянии порождают и крупномасштабные вариации принимаемого сигнала. Вместе с тем, нами экспериментально было установлено [3], что при трансформации многочастотных данных во временную область можно разделить вклад поверхностного рассеяния от рассеяния на зондируемом объекте в эквивалентном псевдоимпульсе:
Такой импульс характеризует относительный вклад рассеяния с разных уровней глубины в соответствии со временем задержки, которому можно сопоставить эффективную глубину zs:
Оказывается, что это преобразование позволяет получить отчетливое изображение рассеивающих объектов в грунте. Поэтому представлялось оправданным выполнить аналогичную (4) трансформацию частотных зависимостей в интегральном уравнении (3) к соответствующим временным распределениям; тогда (3) трансформируется в уравнение, в котором поперечные спектры зависят от параметра эффективной глубины формирования:
Полученное уравнение имеет серьезные преимущества по сравнению с (3). Появляется возможность обоснованно выбрать значения параметра zs так, чтобы они перекрывали интервал, на котором имеется вклад зондируемого объекта – вне зоны влияния поверхности. Кроме того, можно существенно сузить область локализации объекта, в которой ищется решение. Проблема применения развитой теории на практике заключается в определении ядер в уравнениях (3), (6), поскольку не для всех антенн можно определить их вид теоретически. В [2] для этой цели было предложено использовать калибровку ядра уравнения по измерениям тестовых образцов в форме тонких параллелепипедов с известным поперечным спектром и продемонстрирована принципиальная осуществимость метода ближнепольной томографии (восстановления трехмерных распределений комплексной диэлектрической проницаемости) на основе решения (6) – как для распределенных, так и для сплошных (внутренне однородных) тестовых объектов.
Для искомых функций в комплексном гильбертовом
пространстве 
был разработан регуляризирующий алгоритм
решения [2], основанный на принципе обобщенной невязки Тихонова. В результате
из решения в k-пространстве задачи (3) путем
обратного фурье-преобразования получается решение задачи томографии – искомая
трехмерная структура комплексной диэлектрической проницаемости:
. (7)
Однако, поскольку на
практике чаще всего приходится иметь дело со сплошными объектами, больший
интерес представляет задача определения их формы, т.е. задача компьютерной
голографии. Для этого необходимо ввести в алгоритм решения задачи
дополнительную априорную информацию о постоянстве диэлектрических параметров
внутри неоднородной области. Из общих соображений ясно, что такое сильное
ограничение способно привести к существенно более точному решению задачи. Такой
метод голографии был разработан нами в [3,5]; он основан на непосредственном
использовании восстановленного из решения (6) распределения 
в предположении, что оно получено для
объекта с известной постоянной внутренней комплексной диэлектрической
проницаемостью
.
Для этой цели зададим
форму поверхности объекта в декартовой системе координат в виде 
(см. на рис.2). При некотором значении 
сечение описывается двумя функциями: 
– левее пунктирной линии и 
– правее этой линии.
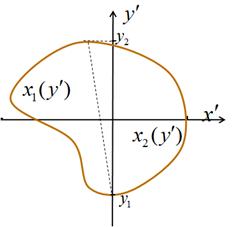
Рис.2. Граница сечения объекта при 
Тогда для одномерного обратного фурье-преобразования этого спектра по ky имеем комплексное уравнение:
решение которого для двух
неизвестных x1 и x2
задает искомую форму поверхности объекта. Поскольку решение может быть получено
при каждом значении kx, уравнение (8) является
переопределенным, и, следовательно, имеется возможность его оптимизации.
Очевидно, что аналогичное уравнение можно получить для описания формы объекта
функциями 
.
3. Результаты численного эксперимента
Численные эксперименты были
выполнены для системы, работающей в диапазоне 200-600 МГц с
приемно-передающей системой, использующей идентичные антенны с размерами 1,5
1,5 см2,
возбуждаемые y-компонентой тока постоянной
амплитуды, и расстоянием между их центрами 2 см. В этом диапазоне толщина
скин-слоя в такой среде меняется примерно от 2 до 6 см.
На рис.3,4 показаны
результаты численного моделирования метода томографии для неоднородности,
имеющей форму параллелепипеда размером 110,5 см3 с e = 43+18i,
основанного на решении (3), в среде с e = 40+15i для двух значений
его глубины: на рис.3 для глубины 1 см, а на рис.4 – для глубины 3 см.
Можно видеть, что на изображении синтезированного псевдоимпульса (рис.3b, 4b) объект виден в
области эффективных глубин рассеяния zs,
примерно соответствующих реальному глубинному положению объекта. Это открывает
возможность существенного сужения области, где ищется решение обратной задачи
рассеяния, что весьма важно в некорректных задачах, основанных на решении
уравнений Фредгольма 1-го рода. На изображениях псевдоимпульса есть и более
слабо выраженные детали, не ассоциируемые с объектом.
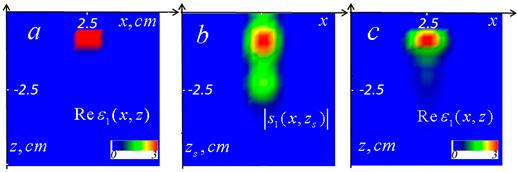
Результаты томографического анализа (рис.3с, 4с), основанные на решении (3) по данным с наброшенной случайной нормально распределенной ошибкой со среднеквадратичным отклонением в 5%, демонстрируют хорошую воспроизводимость положения и формы объекта. Однако, если для объекта на глубине 1 см восстановленное значение диэлектрической проницаемости в максимуме отличается от заданного примерно на 10%, то при его глубине 3 см ошибка составляет около 30%.
|
Рис.3. Моделирование метода томографии для объекта на глубине 1 см. a) исходное распределение диэлектрической проницаемости в вертикальном сечении через центр объекта по оси y; b) распределение амплитуды псевдоимпульса в зависимости от параметра эффективной глубины рассеяния zs; c) восстановленное распределения диэлектрической проницаемости в вертикальном сечении (томограмма). |
|
|
|
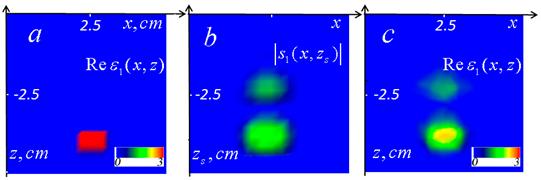
Рис.4. Моделирование томографии объекта на глубине 1 см. Обозначения аналогичны рис.2. |
На томограммах (рис.3с, 4с) так же, как и на изображениях псевдоимпульса можно заметить артефакты, но они являются менее выраженными.
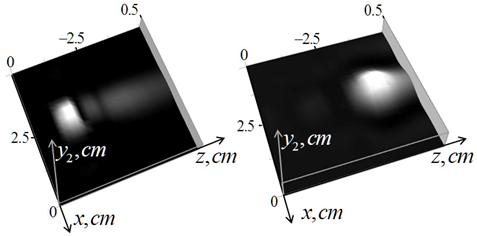
Существенно более отчетливо объект различим на голограммах (рис.5), полученных из решения (8), что возможно связано с введением дополнительной информации о постоянстве его диэлектрической проницаемости. Можно отметить, что с ростом глубины происходит расплывание формы объекта, но артефакты уже практически отсутствуют и в целом достигнутое качество диагностики можно считать приемлемым для рассматриваемых приложений.
|
Рис.5. Моделирование метода голографии. Слева – голографическое изображение половины моделируемого объекта, расположенного на глубине 1 см, функцией y2(x,z); справа – голографическое изображение объекта на глубине 3 см. |
Результаты подтверждают принципиальную возможность решения обратной задачи диагностики объектов с размерами около 1 см для такой среды по данным измерения в выбранном диапазоне с использованием электрически малых антенн. Однако серьезной проблемой является создание системы, обеспечивающей измерения рассеянного поля с необходимым уровнем точности, поскольку уменьшение антенн до таких малых размеров радикально уменьшает эффективность излучения бегущих волн – фактически зондирование осуществляется только ближним полем.
Для исследования формирования
зондирующего и рассеянного поля в описанной выше среде были выполнены их прямые
расчеты для широкополосного диполя типа bow-tie, подобного по структуре антеннам, использованным в
описанной выше системе, которая использовалась нами в [3], но с уменьшенными в
два раза размерами (1,92,8 см2).
Такие антенны предполагается использовать в новой системе для зондирования в
медицинских приложениях. Расчеты проводились для объектов в форме параллелепипеда
с теми же размерами, что и выше (110,5 см3). Однако
оказалось, что для обеспечения различимости рассеянного от объекта сигнала в
такой среде его диэлектрические параметры должны иметь больший контраст, а сами
измерения необходимо выполнять из согласованной по диэлектрическим параметрам
среды. На рис. 6 представлены вычисленные распределения амплитуд полного и
рассеянного полей на частоте 200 МГц в плоскости x-z такой излучающей антенны для объекта с e = 30+5i
в форме параллелепипеда с такими же размерами, как на рис.3,4 и на тех же
глубинах 1 и 3 см.
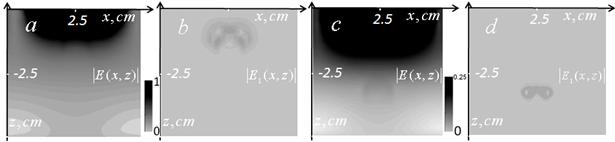
Рис.6. Слева – распределение полного поля (a) и рассеянного поля (b) для объекта на глубине 1 см. Справа – полное (с) и рассеянное (d) поля для объекта на глубине 3 см.
Масштаб рис.6a,b нормирован на амплитуду поля, соответствующему началу сплошной черной зоны на рис.6a, а на рис. 6с,d – на четверть этой величины. Ближе к антеннам поле существенно (на порядки) возрастает. Видно, что объект проявляется в распределениях полного поля на рис.6a,c как слабоконтрастный, что позволяет использовать описанные выше методы решения обратной задачи. Но, с другой стороны, выделение вариаций рассеянного поля (рис.6b,d) на фоне сильного сигнала вблизи излучающей антенны остается серьезной технической проблемой, возможность решения которой предстоит выяснить на основе экспериментальных исследований.
Решение указанной проблемы существенно облегчается в случаях, когда диэлектрические параметры живой ткани не слишком велики – как например, в при зондировании опухолей в жировой ткани грудной железы (e = 12+2i). Тогда для диагностики можно использовать более высокочастотный диапазон, в частности, такой же, как и в [3] (1,7 ГГц – 7 ГГц). В этом интервале частот толщина скин-слоя меняется в диапазоне от 2 до 10 см. На рис. 7 показаны распределения амплитуд полного и рассеянного полей на частоте 2 ГГц в плоскости x-z такой излучающей антенны для опухолевой ткани в жировой среде в форме параллелепипеда с такими же размерами, как на рис. 6 и на тех же глубинах 1 и 3 см.
Рис.7. Слева – распределение полного поля (a) и рассеянного поля (b) для объекта на глубине 1 см. Справа – полное (с) и рассеянное (d) поля для объекта на глубине 3 см.
Из сравнения результатов рис.7 с распределениями полей на рис. 6 можно видеть, что относительный вклад рассеянного поля в полное поле существенно (на порядки) возрастает; при этом для объекта на малой глубине он даже становиться сопоставим с вкладом зондирующего поля, что безусловно облегчает создание эффективной системы для зондирования в медицинской диагностики.
Исследования были выполнены при поддержке РФФИ, проекты № 12-02-90028-Bel, 13-07-97028_р_поволжье, БРФФИ № Т12Р-133, а также программы ОФН РАН IV.13, а также частично поддержаны грантом Минобрнауки РФ (соглашение от 27 августа 2013г. № 02.В.49.21.0003 между МОН РФ и ННГУ).
1. Gaikovich K.P. Subsurface Near-Field Scanning Tomography, Physical Review Letters, 2007, v. 98, No. 18, pp. 183902 (1-4).
2. Gaikovich K.P., Gaikovich P.K. Inverse problem of near-field scattering in multilayer media, 2010, Inverse Problems, v. 26, No. 12, pp. 125013 (1-17 pp.).
3. Gaikovich K.P., Gaikovich P.K., Maksimovitch Ye.S., Badeev V.A. Pseudopulse near-field subsurface tomography, Physical Review Letters, 2012, v. 108, No.16, p. 163902 (1-5).
4. Razevig V. V., Ivashov S. I., Sheyko A. P., Vasiliev I. A., Zhuravlev A. V. An example of holographic radar using at restoration works of historical building, Progress in Electromagnetic Research Letters, 2008, v.1, pp. 173-179.
5. Гайкович К.П., Максимович Е.С., Бадеев В.А. Микроволновая подповерхностная голография сплошных диэлектрических объектов. Журнал радиоэлектроники [электронный журнал], 2012, №6, http://jre.cplire.ru/jre/jun12/index.html.