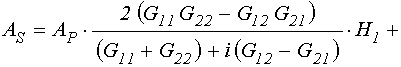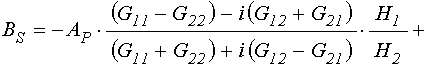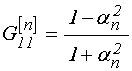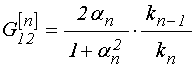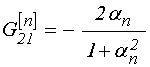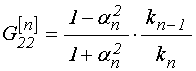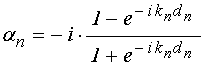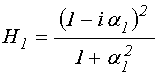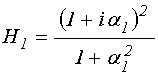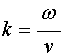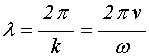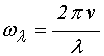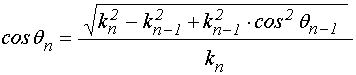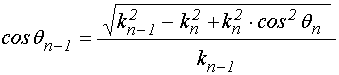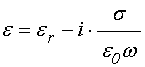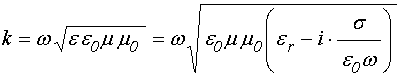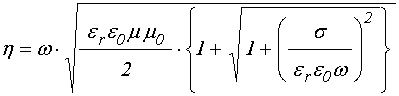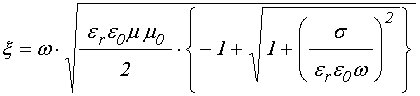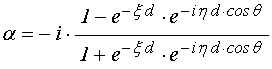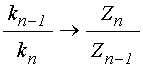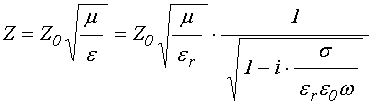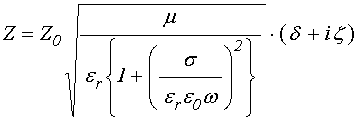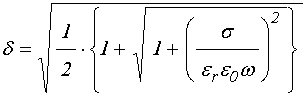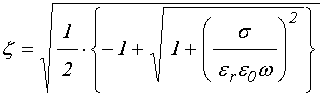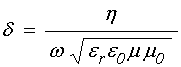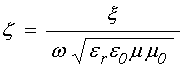УДК 537.874; 537.624
ИССЛЕДОВАНИЕ МЕТОДОМ ИСКЛЮЧЕНИЯ РАСПРОСТРАНЕНИЯ ВОЛН ЧЕРЕЗ МНОГОСЛОЙНУЮ СРЕДУ С БАРЬЕРНЫМИ НЕОДНОРОДНОСТЯМИ
И. В. Антонец1, В. Г. Шавров2, В. И. Щеглов2
1Сыктывкарский государственный университет, Сыктывкар
2Институт радиотехники и электроники РАН, Москва
Статья получена 13 января 2015 г.
Аннотация. Методом исключения рассмотрена задача о распространении волн через многослойную структуру, содержащую барьерные и периодические неоднородности. Получены частотные зависимости коэффициентов отражения, прохождения и поглощения. Выявлен периодический многолепестковый характер зависимостей коэффициентов от частоты, показана его связь с параметрами барьеров. Рассмотрено распространение волны в структуре с периодической неоднородностью на модели многобарьерной среды. На каждом периоде частотных зависимостей коэффициентов выявлено выделение одного узкого лепестка при подавлении боковых лепестков. При увеличении числа барьеров центральная частота лепестка увеличивается, его ширина уменьшается, а амплитуда увеличивается, причем эти изменения происходят тем сильнее чем соотношение скоростей внутри и вне барьера больше. Обнаружен эффект вторичной модуляции частотной зависимости, для интерпретации которого высказана гипотеза о биениях между резонансами в барьерах и промежутках между ними. Показана возможность обобщения на случай электромагнитных волн, распространяющихся в проводящей среде с магнитной и диэлектрической проницаемостями.
Ключевые слова: распространение волн, многослойные неоднородные структуры.
Abstract. The task of wave propagation through multilayer structure containing barrier and periodic nonuniformities is solved by exclusion method. The frequency dependencies of reflection, transmission and absorption coefficients are found. The periodic multipetal character of frequency dependencies and its connection with barrier parameters is found. It is investigated the wave extension in structure with periodic nonuniformity on the model of multibarrier medium. On each period of coefficient frequency dependencies it is found the separation of single narrow petal accompanied by the suppression of side petals. When the quantity of barriers is increased the central frequency of petal is increased and its amplitude is decreased. These changing are the stronger the distinction between the velocities inside and outside of barriers is more. The secondary modulation effect of frequency dependencies is found. For interpretation of this effect it is proposed the hypothesis about the beating between the resonances inside and outside of barriers. It is shown the possibility of generalization on the case of electromagnetic waves propagating in conducting media with permittivity and permeability.
Key words: wave propagation, multilayer nonuniform structure.
Введение
Распространение волн различной природы через слоистые и неоднородные среды издавна привлекает внимание исследователей [1-6]. Особое место здесь занимают задачи, где неоднородность имеет периодический характер [7], возникающие во множестве в электро и радиотехнике, в теории связи, колебаний, теории распространения упругих, электромагнитных или электронных волн в кристаллах и ряде других областей. Значительное количество задач касается распространения электромагнитных и магнитостатических волн в магнитных средах [8-14]. Характерным свойством всех периодических сред является наличие чередующихся по частоте полос пропускания и непропускания [7].
Для решения подобных задач особенно широко используются методы, основанные на решении уравнений Хилла, Матье или Кронига-Пенни [7,15-17], специфически весьма удачно приспособленные к периодическому характеру среды. Однако в случае хотя бы небольшого нарушения периодичности, например при возникновении какого-нибудь промежуточного барьера, приходится использовать уже классические методы решения задач для сред с произвольными неоднородностями. Наиболее последовательным здесь является прямой метод, состоящий в решении волновых уравнений в каждом слое с последующим их сшиванием на границах [3,4,18,19]. Удобным обстоятельством для этого метода является возможность его применения для волн разнообразной природы, в первую очередь электромагнитных [19,20]. Тем не менее, свойственные этому методу трудности раскрытия громоздких определителей высоких порядков делают его непригодным уже при количестве сред более пяти.
Методы последовательных вычислений – матрицы [18,21], импеданса [1,2,22] и некоторые специфические, в том числе метод переотражений [23], хотя и являются менее громоздкими, однако пригодны для рассмотрения за один проход волн только одного направления без учета встречных волн. Алгоритм последовательного построения решения для произвольного числа слоев [24-27] удобен для получения аналитических выражений, однако на каждом шаге объем вычислений удваивается, что затрудняет его применение для структур, содержащих более пяти-шести сред.
Для задач, где достаточно получить амплитуды отраженной и проходящей волн, значительное преимущество в простоте и универсальности имеет метод исключения, подробно рассмотренный в работе [28]. Будучи пригодным для неоднородностей любого вида, он применим как для идеально периодических структур, так и при частичном нарушении периодичности, а также в случае любых видов затухания.
В работе [29] метод исключения весьма успешно применен для изучения распространения волн в средах с барьерными и периодическими неоднородностями. Однако проведенное там исследование является неполным. Так недостаточно исследован характер отраженных и проходящих волн при большом числе барьеров, не рассмотрено влияние затухания волн на структуру характеристик отражения и прохождения, а также на свойства отмеченного там эффекта вторичной модуляции. Применимость полученных результатов к случаю электромагнитных волн не рассмотрена.
Настоящая работа является продолжением исследования, выполненного в [29], c более подробным выявлением отмеченных особенностей, а также рассмотрением применимости полученных результатов к случаю электромагнитных волн, распространяющихся в проводящей среде с магнитной и диэлектрической проницаемостями.
1. Геометрия задачи и схема барьерной неоднородности
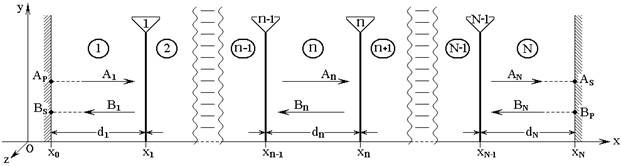
Рассмотрим падение двух встречных одномерных волн на многослойную структуру, состоящую из произвольного числа плоскопараллельных сред. Геометрия задачи, совпадающая с принятой в [28,29], показана на рис.1.
Рис.1. Геометрия распространения встречных одномерных волн.
Структура содержит 
сред, представляющих собой плоские однородные
бесконечно протяженные пластины, разделенные 
бесконечно
тонкими границами. Плоскость 
декартовой системы
координат 
параллельна плоскостям пластин, а ось 
им перпендикулярна. Координаты границ равны
, 
, …, 
, расстояния между ними: 
. Вдоль оси распространяются
плоские одномерные волны волновые числа которых равны 
,
, . . . , 
.
Амплитуды волн, распространяющихся в прямом направлении, обозначены 
, во встречном – 
.
Будем полагать, что структура представляет собой совокупность слоев, каждый из которых в отдельности однороден, а на границах между слоями параметры соседствующих сред скачком меняются, причем это изменение может происходить в обе стороны, то есть волновое число распространяющейся волны может как увеличиваться, так и уменьшаться. С точки зрения распространения волны такую структуру можно рассматривать как совокупность примыкающих друг к другу прямоугольных барьеров разной высоты, поэтому будем называть ее «структурой с барьерной неоднородностью».
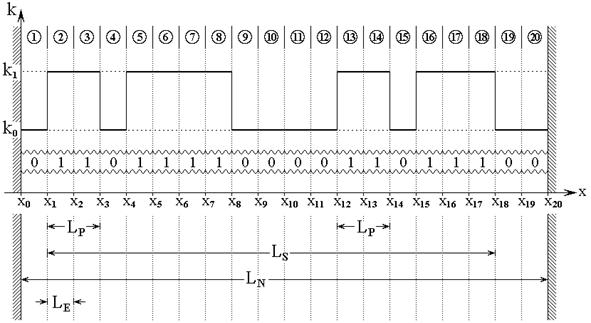
Рис.2. Схема многослойной структуры с барьерной неоднородностью.
На рис.2 показана схема
рассматриваемой далее такой структуры. Исследуемая структура содержит 20 сред
(номера показаны цифрами в кругах), границы между которыми соответствуют
координатам , , . . .
. 
. Утолщенными горизонтальными линиями
показана зависимость волнового числа от координаты. Волновые числа внутри сред
принимают два значения 
и ,
причем в первой и последней средах волновое число равно .
Структура содержит
несколько барьеров, для обращения к которым будем использовать обозначение 
, где 
–
координата начала барьера, 
– координата его конца.
Так для барьера между координатами и 
будем использовать обозначение 
, для барьера между координатами 
и 
– обозначение
, для барьера между 
и 
–
обозначение 
и между 
и 
– 
.
Последовательное распределение волновых чисел по слоям структуры можно
характеризовать заданием последовательности нулей и единиц, в которой нуль
соответствует , а единица – . Такая последовательность показана на
рисунке между двумя волнистыми линиями и имеет вид: 01101111000011011100.
Структура может содержать
несколько барьеров различной длины. Для дальнейшего рассмотрения важны два
параметра: минимальная длина барьера 
, соответствующая
самому короткому барьеру, а также полная длина неоднородности 
, соответствующая расстоянию от начала
первого барьера до конца последнего. При этом полную длину структуры будем
обозначать 
. Для интерпретации описанных далее
результатов удобно ввести понятие «элементарного барьера». Полагая толщины всех
слоев структуры равными друг другу, будем называть «элементарным барьером»
такой барьер, длина которого равна толщине одного слоя. Длину элементарного
барьера обозначим через 
. В общем случае 
.
В качестве частного
случая барьерной неоднородности можно рассматривать структуру, состоящую из
нескольких одинаковых барьеров, расположенных периодически. В случае такой
периодической структуры будем полагать, что внутри барьеров волновое число
равно , а между ними – .
2. Метод исключения
При работе методом
исключения [28] для каждой среды рассматриваются две волновые функции, одна из
которых является суммой прямой и встречной волн, а другая – частным от деления
производной от первой на волновое число. Вся структура разбивается на ячейки,
каждая из которых включает в себя одну среду и одну границу. После нахождения
соотношений между упомянутыми функциями на внешних сторонах каждой ячейки,
полученные соотношения сшиваются «прикладыванием» друг к другу, в результате
чего амплитуды внутренних волн исключаются. Для структуры в целом получается
система из двух линейных уравнений, связывающая неизвестные амплитуды выходящих
волн 
и 
с
заданными амплитудами входящих 
и 
, коэффициенты в которой выражаются через
параметры сред. Решение этой системы имеет вид:
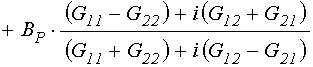; (1)
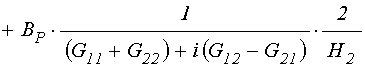, (2)
где функции 
(верхний
индекс «
» для простоты записи опущен). Для 
и 
эти
функции определяются по формулам:
где
а все последующие функции 
, начиная с 
(то
есть 
), получаются из предыдущих с помощью
рекуррентных формул:
При этом функции 
равны:
3. Энергетические параметры распространения волн
Найденные амплитуды
отраженной и проходящей волн и позволяют определить энергетические
коэффициенты, характеризующие распространение волны. Для случая падения одной
волны в положительном направлении оси 
, то
есть при 
, 
, энергетические
коэффициенты отражения 
, прохождения 
и поглощения 
имеют
вид:
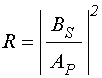; (14)
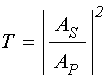; (15)
. (16)
4. Зависимость от частоты и диссипации среды
Метод исключения предполагает заданными волновые числа в отдельных средах, тогда как основной задачей дальнейшего рассмотрения является исследование частотных свойств структуры в целом. Для получения частотной зависимости амплитуд отраженной и падающей волн, введем зависимость волнового числа от частоты через скорость волны с помощью соотношения:
то есть будем считать, что при постоянной скорости и изменяющейся частоте волновое число меняется прямо пропорционально частоте.
При этом длина волны равна:
Если задана скорость и известна длина волны, то частоту, при которой волна принимает заданную длину, можно определить из соотношения:
Так, при 
длине
волны 
соответствует частота 
, а длине волны 
соответствует
частота 
.
Затухание волны за счет
диссипативных свойств среды будем учитывать путем введения мнимой добавки 
к действительной части 
волнового числа, которое в этом случае
становится комплексным:
где 
и 
– величины действительные.
5. Прохождение волны через единичный барьер
Рассмотрим сначала общий
характер распространения волны через среду с единственной неоднородностью в
виде прямоугольного барьера, внутри которого и по обе стороны от него среда
однородна, причем параметры сред по разные стороны от барьера одинаковы, а
внутри барьера принимают отличное значение. Будем считать, что вне барьера
скорость волны равна 
, а внутри барьера – 
, что соответствует волновым числам 
и 
. Поскольку
барьер всего один, то длина неоднородности равна длине этого барьера: 
. Общие свойства распространения волны
через барьер иллюстрируются рис.3, где показаны зависимости коэффициентов
отражения (1), прохождения (2) и поглощения (3) от частоты при различных
значениях комплексного волнового числа.
Рис.3. Зависимости коэффициентов отражения (1), прохождения (2) и поглощения (3) от частоты для единичного барьера при комплексном волновом числе.
Параметры: 
;
, 
; 
.
а – 
; б – 
;
в – 
; г – 
.
Рис.3а соответствует
чисто действительному волновому числу: 
, 
. Из этого рисунка видно, что обе зависимости
и 
имеют
осциллирующий периодический вид, близкий к синусоидальному, причем минимумы
отражения приходятся на максимумы прохождения. Зависимости и симметричны
относительно уровня 
, а коэффициент поглощения 
всегда равен нулю. При изменении частоты
амплитуды осцилляций зависимостей и сохраняются постоянными. Из численной
оценки следует, что коэффициент отражения максимален
тогда, когда длина барьера равна нечетному числу четвертей длин волн внутри
барьера, и минимален тогда, когда эта длина равна четному числу четвертей длин
волн. При этом первый минимум зависимости при 
, определяющий величину ее периода, соответствует
равенству между длиной барьера и половиной длины волны внутри него.
Вследствие симметрии
зависимостей относительно уровня , для коэффициента
прохождения эти соотношения заменяются на обратные.
Рис.3б соответствует
случаю, когда волновое число уже имеет мнимую часть, однако она значительно
меньше действительной: 
. Как и в предыдущем
случае здесь зависимости и осциллируют с тем же периодом, однако по
мере увеличения частоты амплитуда осцилляций спадает, при этом коэффициент
отражения стремится к постоянному значению 
, а коэффициент прохождения стремится к нулю. Коэффициент поглощения
резко возрастает, стремясь к постоянному значению 
.
Затухание осцилляций до уровня 
от максимума происходит
при частоте 
.
Рис.3в соответствует
случаю, когда мнимая часть волнового числа имеет тот же порядок, что и
действительная: 
. Здесь осцилляции коэффициентов
прохождения и поглощения полностью пропадают, а коэффициент отражения,
претерпевая лишь одно незначительное переколебание, принимает постоянное
значение 
. Коэффициент прохождения падает до нуля,
а коэффициент поглощения стремится к величине 
. Стабилизация
режимов происходит при частоте порядка 
. Таким
образом, начиная с этой частоты, поглощение энергии преобладает над отражением.
Рис.3г соответствует
случаю, когда мнимая часть волнового числа значительно превышает
действительную: 
. Здесь какие-либо осцилляции
также полностью отсутствуют, стабилизация режимов происходит уже при частоте
порядка 
, причем теперь уже отражение значительно
преобладает над поглощением.
Замечание. Рассмотренная картина в случае электромагнитных волн для барьера в пустом пространстве соответствует различным видам проводимости составляющей барьер среды. Так рис.3а соответствует диэлектрику, рис.3б – полупроводнику с малой проводимостью, рис.3в – полупроводнику с высокой проводимостью, рис.3г – металлу.
6. Изменение длины единичного барьера
Рассмотрим теперь, что
происходит с волной при изменении длины барьера. Поскольку основной характер
частотных зависимостей при комплексном волновом числе уже выяснен, ограничимся
рассмотрением действительного волнового числа. Из рис.3а следует, что в этом
случае частотные зависимости коэффициента отражения и прохождения симметричны
относительно уровня . Поэтому достаточно будет
рассмотреть только коэффициент отражения. Характер поведения коэффициента
отражения 
при изменении длины барьера 
иллюстрируется рис.4, где приведены
зависимости для барьеров длиной от 
до 
с
шагом в 
.
Для удобства построения
наглядных рисунков, скорость волны внутри барьера выбрана близкой к единице: 
. При этом скорость волны вне барьера, как
и прежде, равна 
. Столь малое различие между
скоростями внутри и вне барьера порождает довольно малое значение коэффициента
отражения, порядка 
, что однако никак не мешает
проследить основные закономерности во всех подробностях.
Если задана скорость и
известна длина волны, то частота, при которой волна имеет заданную длину,
определяется соотношением: 
. Так при длине волны соответствует
частота 
, а длине волны 
соответствует
частота 
. Эти значения частот показаны на рис.4
вертикальными точечными линиями.
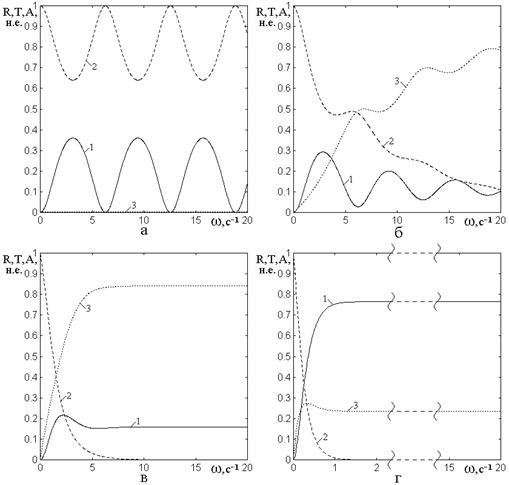
Из рис.4 видно, что зависимость коэффициента отражения от частоты при любой длине барьера является периодической, близкой к синусоидальной.
Рис.4а соответствует
длине барьера 
. Видно, что первый минимум
зависимости приходится на частоту . Длина волны, соответствующая этой частоте,
равна 
. Отражение становится минимальным на той
частоте, на которой половина длины волны становится равной длине барьера, как
это отмечалось в предыдущем разделе. Второй минимум приходится на частоту,
соответствующую двум длинам волн на длине барьера и так далее, то есть период
зависимости равен .
Рис.4б соответствует
увеличению длины барьера до , то есть в два раза.
При этом первый минимум приходится на частоту вдвое ниже, то есть на 
. Остальные минимумы кратны этой величине,
то есть период здесь становится вдвое короче.
Рис.4в соответствует
увеличению длины барьера до 
, рис.4г – 
, рис.4г – 
. Во
всех этих случаях период уменьшается в число раз, равное отношению длины
барьера к первоначальной в 
, соответствующей минимальной
длине барьера.
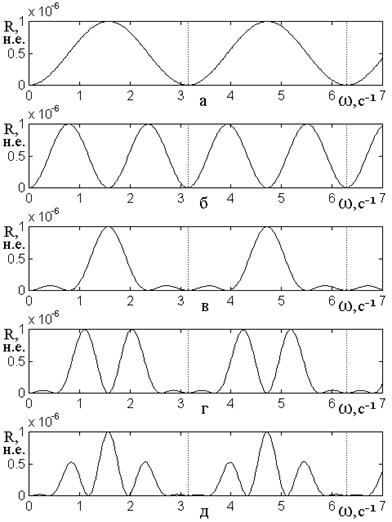
Рис.4. Зависимости коэффициента
отражения от частоты для барьеров разной длины. Вне барьера: , внутри барьера: .
Длина
барьера: а – ; б – ; в – ; г – ; д – 
.
Таким образом, можно
сказать, что при увеличении длины барьера первоначальная зависимость разбивается на одинаковые «лепестки»,
количество которых на длине первоначального периода равно отношению длины барьера
к его первоначальной длине.
7. Прохождение волны через два единичных барьера
Рассмотрим теперь, что происходит с коэффициентом отражения в случае двух барьеров при различной их длине и расположении.
Характер поведения
коэффициента отражения при изменении расстояния между
двумя одинаковыми барьерами иллюстрируется рис.5, где приведены зависимости для барьеров длиной , расстояние между началами которых
меняется от 
до с шагом
в . Зависимости нормированы на единицу
(нормирующие множители приведены в подписи к рисунку). Для удобства сравнения с
предыдущим случаем, скорость волны внутри барьеров выбрана равной: . При этом скорость волны вне барьеров
по-прежнему равна . Частоты и , соответствующие
длинам волн и ,
отмечены на рис.5 вертикальными точечными линиями.
Из рис.5 видно, что
зависимость коэффициента отражения от частоты при любом расстоянии между
барьерами является периодической, причем величина периода всегда остается одной
и той же равной , в данном случае определяемой
длиной одного барьера. Однако близкий к синусоидальному характер зависимости наблюдается только для случаев 5а и 5б, а
в случаях 5в, 5г, 5д зависимости имеют вид синусоиды, промодулированной по
амплитуде другой синусоидой с периодом .
Рис.5а и 5б совпадают с
рис.4а и 4б и никаких новых закономерностей не выявляют. Рис.5б на длине
периода содержит два лепестка, рис.5в – три лепестка, рис.5г – четыре, а рис.5д
– пять лепестков, то есть здесь, подобно случаю, изображенному на рис.4, при
увеличении расстояния между барьерами, то есть при увеличении полной длины
неоднородности первоначальная зависимость разбивается на одинаковые лепестки,
количество которых на длине первоначального периода равно отношению полной
длины неоднородности к длине одного барьера: 
.
Рис.5. Зависимости коэффициента
отражения от частоты для двух барьеров на различном расстоянии. Скорости: , 
. Длины
барьеров: . Параметры с нормирующим множителем:
а – 
, ; 0100000000…0; ,
; 
;
б – , 
; 0110000000…0; 
,
; ;
в – , 
; 0101000000…0; 
,
; 
;
г – , 
; 0100100000…0; 
,
; 
;
д – , 
; 0100010000…0; 
,
; .
Внутри каждого периода
лепестки располагаются симметрично относительно центра периода, а их амплитуда
по мере приближения к краям периода убывает. При нечетном отношении период содержит один центральный лепесток,
амплитуда которого значительно превышает амплитуды остальных. При четном
отношении в центре периода коэффициент отражения равен
нулю, а по бокам симметрично располагаются два лепестка, амплитуда которых
значительно преобладает над остальными.
Таким образом, можно
сделать вывод, что в рассматриваемом случае величина периода определяется
длиной одного барьера , а количество лепестков внутри
периода определяется отношением полной длины неоднородности к длине одного барьера: . Поскольку в данном случае минимальная длина
барьера равна длине элементарного барьера , величина эквивалентна
величине 
.
8. Два барьера различной длины
Рассмотрим теперь, что
происходит с коэффициентом отражения в случае двух барьеров при изменении их
длины. Характер поведения частотной зависимости коэффициента отражения при изменении длины каждого из двух
барьеров иллюстрируется рис.6. Зависимости нормированы на единицу (множители –
в подписи). Для единства с предыдущими случаями скорости волны внутри и вне
барьеров выбраны равными: 
, 
. Частоты и , соответствующие и
, отмечены вертикальными точечными
линиями.
Из рис.6 видно, что
зависимость коэффициента отражения от частоты при любом расстоянии между
барьерами является периодической, причем величина периода всегда остается
равной , в данном случае определяемой уже не
минимальной длиной барьера , поскольку она
меняется, а толщиной одного слоя или длиной элементарного барьера , равной 
.
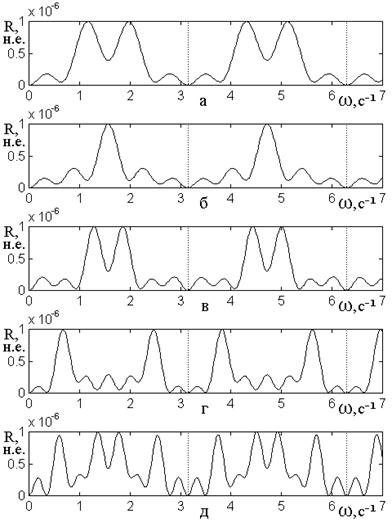
Рис.6. Зависимости коэффициента
отражения от частоты для случая двух барьеров различной длины. Скорости: , .
Параметры с нормирующим множителем:
а – , 
; 0101100000…0; 
,
; 
;
б – , 
; 0101110000…0; 
,
;;
в – , 
; 0101111000…0; 
,
;
;
г – 
, 
; 0110011100…0; 
,
;
;
д – 
, 
; 0111011110…0; 
,
;
.
Характер зависимости во всех случаях имеет многолепестковый
вид, напоминающий синусоиду с переменной амплитудой. Внутри каждого периода
лепестки располагаются симметрично относительно центра периода. Полное
количество лепестков на длине периода равно отношению полной длины неоднородности
к длине элементарного барьера .
9. Произвольное количество и длина барьеров
Для многослойной структуры, все слои которой имеют одинаковую толщину, а скорость волны принимает всего два значения: одно вне барьеров, другое внутри них, отмеченные выше закономерности выполняются при любом произвольном количестве, длине и расстоянии между барьерами. Перечислим эти закономерности в кратком виде.
Зависимость коэффициента
отражения от частоты является периодической. Величина периода соответствует
частоте 
, при которой половина длины волны,
равняется длине элементарного барьера: 
.Зависимость
имеет многолепестковый вид, напоминающий
синусоиду с переменной амплитудой. Внутри каждого периода лепестки
располагаются симметрично относительно центра периода. Полное количество
лепестков на длине периода равно отношению полной длины неоднородности к длине
элементарного барьера .
10. Периодическая неоднородность из единичных барьеров
Важным частным случаем барьерной неоднородности является периодическая, при которой многослойная структура представляет собой совокупность слоев одинаковой толщины с чередующимися параметрами, то есть периодическую последовательность одинаковых барьеров.
Для характеристики
периодической структуры введем еще один параметр – длину периода структуры 
, то есть такое расстояние по оси , по прохождении которого свойства
структуры повторяются.
11. Малое количество барьеров
Рассмотрим сначала, как
ведет себя коэффициент отражения при различном количестве барьеров. Характер
поведения частотной зависимости коэффициента отражения при
изменении количества барьеров иллюстрируется рис.7. Все зависимости нормированы
на единицу (множители – в подписи к рисунку). Для единства с предыдущими
случаями скорости волны внутри и вне барьеров выбрана равными: , . Частоты
и ,
соответствующие и 
, отмечены
вертикальными точечными линиями.
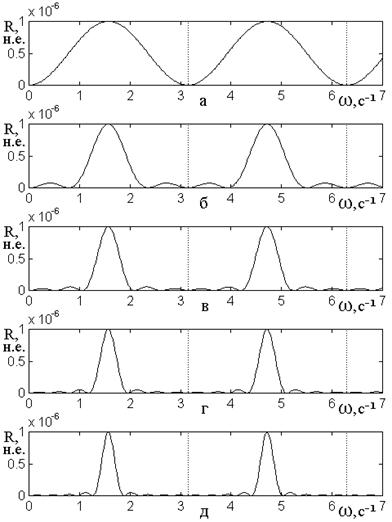
Рис.7а соответствует одному барьеру и совпадает с рис.3а. Рис.7б соответствует двум барьерам, рис.7в – трем, рис.7г – четырем, рис.7д – пяти.
Из рис.7 видно, что
зависимость коэффициента отражения от частоты имеет те же свойства, что и при
произвольной структуре, то есть при любом количестве барьеров является
периодической с периодом , определяемой длиной
элементарного барьера 
. При этом зависимость во всех случаях имеет многолепестковый
вид, причем внутри каждого периода лепестки располагаются симметрично
относительно его центра. Количество лепестков на длине периода равно .
Везде значительно
выделяется центральный лепесток, приходящийся на середину периода, причем с
увеличением количества барьеров отношение амплитуды первого бокового лепестка к
амплитуде центрального уменьшается. Так при двух барьерах это отношение составляет
, при трех – 
, а при
четырех-пяти – около 
. Ширина центрального лепестка
на уровне половины высоты при увеличении числа барьеров уменьшается. При одном
барьере она составляет 
, при двух – 
, при трех – 
, при
четырех – 
и при пяти – 
.
Рис.7. Зависимости коэффициента
отражения от частоты для периодической структуры с разным числом барьеров. Параметры:
, ; 
; 
; 
.
а – 1; 01000000000…0; 
; ;
б – 2; 01010000000…0; 
; ;
в – 3; 01010100000…0; 
; 
;
г – 4; 01010101000…0; ; 
;
д – 5; 01010101010…0; 
; 
.
12. Увеличение количества барьеров, частотные параметры
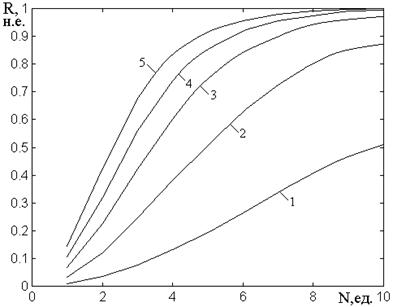
Ввиду практической важности распространения волны через периодическую структуру, рассмотрим этот вопрос более подробно, для чего зададим сразу достаточно большое число барьеров, чтобы основные особенности выявились более наглядно. Такая ситуация иллюстрируется рис.8, где показаны зависимости частотных параметров главного лепестка от количества барьеров при различных соотношениях скоростей волн вне и внутри барьеров.
Порядок расположения
барьеров при различном их числе принят следующим: 
:
01000000000…0000; 
: 01010000000…0000; далее барьеры
прибавляются по одному через каждый промежуток; при десяти барьерах порядок
имеет вид: 
: 01010101010101010101.
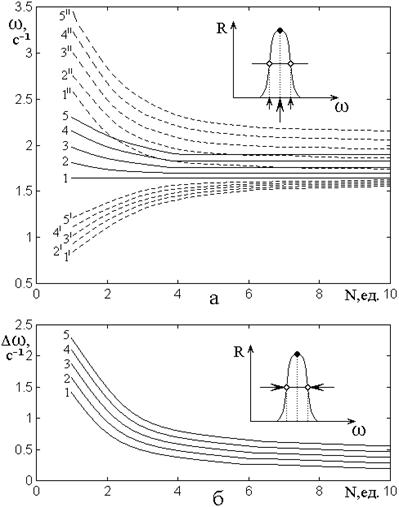
Рис.8. Зависимости частотных параметров главного
лепестка от количества барьеров при различных
соотношениях скоростей волн вне и внутри барьеров. а – центральная частота
(сплошные линии) и частоты краев (пунктир) лепестка; б – ширина лепестка на половине
его высоты. На врезках показаны схемы получения значений частот. Общие параметры:
,; ; ; . Индивидуальные
параметры:
1 – 
; 2 – 
; 3 – 
;
4 – 
; 5 – 
.
Из рис.8а видно, что по
мере увеличения числа барьеров центральная частота лепестка (сплошные линии)
несколько уменьшается, причем это уменьшение тем более заметно, чем различие
скоростей внутри и вне барьеров больше. Так при соотношении скоростей равном 
(сплошная кривая )
центральная частота в пределах точности рисунка не меняется, тогда как при соотношении
равном 
(сплошная кривая 
),
частота центра лепестка при одном барьере составляет 
,
а при десяти барьерах – 
, то есть уменьшается
на 
от первоначальной величины.
Частота нижнего края
лепестка на половине его высоты (цифры с одним штрихом) по мере увеличения
числа барьеров увеличивается, а верхнего (цифры с двумя штрихами) уменьшается.
Такое изменение также происходит наиболее сильно при числе барьеров до четырех,
где составляет до 
, а уже после шести барьеров
вплоть до десяти меняется мало – не более чем на 
.
На рис.8б показана
зависимость ширины лепестка от числа бартеров, полученная как разность частот
верхнего и нижнего краев на рис.8а. Видно, что при увеличении числа барьеров лепесток
сужается, особенно сильно при малом их числе, причем это сужение более ярко
проявляется при большем соотношении скоростей волн внутри и вне барьеров (наиболее
сильно для кривой 5, где это соотношение равно ). Так
при увеличении числа барьеров от одного до четырех для кривой 5 сужение
лепестка составляет 
, а при увеличении числа
барьеров от шести до десяти – всего 
от начальной величины.
13. Амплитудные параметры
Рассмотрим теперь
зависимости амплитуды главного лепестка от количества барьеров при различных соотношениях скоростей волн
вне и внутри барьеров, иллюстрируемые рис.9.
Рис.9. Зависимости амплитуды главного
лепестка от количества барьеров при различных
соотношениях скоростей волн вне и внутри барьеров.
Все параметры – те же, что на рис.8.
Из этого рисунка видно,
что амплитуда главного лепестка при увеличении числа барьеров растет тем
сильнее, чем соотношение скоростей волн внутри и вне барьеров больше. Так при
соотношении равном (кривая 1), амплитуда главного
лепестка достигает величины 
только при десяти
барьерах, тогда как при соотношении 
(кривая 5), достигает
почти той же величины (точнее 
) уже при двух
барьерах. Все кривые стремятся к максимуму отражения 
,
приближаясь к этому значению тем скорее, чем количество барьеров и соотношение
скоростей больше. Так при соотношении скоростей равном (кривая
5) практически полное отражение 
наступает уже при восьми
барьерах, а при десяти становится равным 
.
Таким образом, можно видеть, что при увеличении числа барьеров центральная частота главного лепестка частотной зависимости коэффициента отражения несколько увеличивается, его ширина уменьшается, а амплитуда увеличивается в значительной степени, стремясь к единице, причем эти изменения происходят тем сильнее чем соотношение скоростей внутри и вне барьера больше.
14. Влияние диссипации среды
В предыдущих разделах рассматривалось распространение волны в многобарьерной среде, полностью бездиссипативной. Рассмотрим теперь, как меняется отражение и прохождение волны в среде с затуханием, которое будем учитывать введением в волновое число мнимой добавки в результате чего это число будет комплексным.
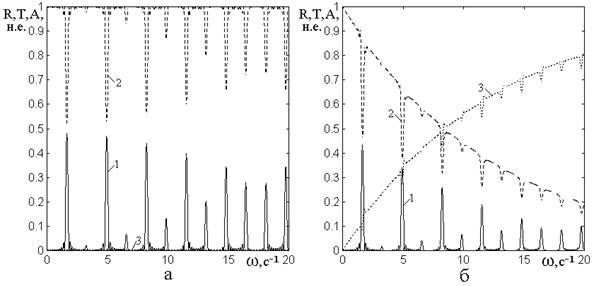
Для этого обратимся к рис.10, где показаны зависимости коэффициентов отражения (1), прохождения (2) и поглощения (3) от частоты для структуры с девятью барьерами. Рис.10а соответствует действительному волновому числу, рис.10б – комплексному.
Рис.10. Зависимости коэффициентов
отражения (1), прохождения (2) и поглощения (3) от частоты для структуры с
девятью барьерами при комплексном волновом числе. Параметры: 
, 
; ; ; 
; ;
01010101010101010100.
а – 
, 
;
б – 
, 
.
Из рис.10 видно, что
главные особенности частотных зависимостей коэффициентов , , , отмеченные при рассмотрении
рис.3,
сохраняются, однако имеется ряд отличий, на которых здесь и остановимся.
Из рис.10а и 10б видно,
что при достаточно большом числе барьеров периодичность всех зависимостей , и по частоте сохраняется. Величина периода
равна 
, что полностью соответствует скорости . Однако амплитуда пиков упомянутых
зависимостей меняется. Так кроме пиков при 
, где 
, появляются также пики при 
, причем из рис.10а видно, что амплитуда
первых пиков с увеличением частоты спадает, а вторых – увеличивается. Вблизи 
амплитуды обоих пиков становятся равными
друг другу, после чего амплитуда первых пиков растет, а вторых – уменьшается
(за правой рамкой рисунка). Ширина тех и других пиков остается постоянной.
При приобретении волновым
числом мнимой добавки, как видно из рис.10б, эта картина, в основном,
сохраняется, причем величина коэффициентов отражения и
прохождения уменьшается, а коэффициента поглощения увеличивается, подобно тому, как это
происходит на рис.3б. Отметим, что здесь при примерно такой же тенденции изменения
этих коэффициентов, мнимая часть волнового числа составляет всего 
, что соответствует 
от действительной части, тогда как на
рис.3б мнимая часть равна 
от действительной.
Такое различие обусловлено тем, что структура на рис.3б содержит всего один
барьер, тогда как здесь их – девять, в результате чего эффект затухания волны, обусловленный
мнимой частью волнового числа, здесь накапливается.
15. Вторичная модуляция
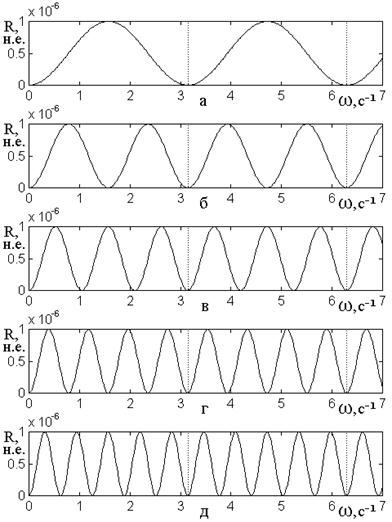
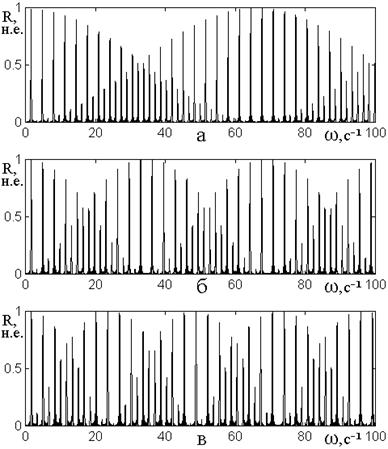
Поскольку амплитуда пиков зависимостей коэффициентов от частоты меняется, представляет интерес рассмотреть их изменение в более широком диапазоне частот. Характер такого изменения иллюстрируется рис.11, где показаны зависимости нормированного коэффициента отражения от частоты в широком диапазоне частот.
Рис.11. Зависимость коэффициента
отражения от частоты при различных значениях скорости волны внутри барьера. Структура
– та же, что на рис.8. Волновое число – действительное. Скорость вне барьера:. Скорости внутри барьера и нормирующие
множители: а – 
, 
; б – , 
; в – 
, 
.
Остальные параметры – те же, что на рис.10.
Из рис.11 видно, что
огибающие частотных зависимостей амплитуд пиков коэффициента отражения
испытывают периодическую модуляцию, период которой зависит от скорости волны
внутри барьера и для рис.11а составляет 
, для
рис.11б – 
и для рис.11в – 
.
Следуя [29], будем называть это явление «вторичной модуляцией». Таким образом,
период вторичной модуляции при увеличении скорости волны внутри барьера
уменьшается.
Отметим попутно, что в
пределах диапазона исследованных значений ,
абсолютные значения максимумов коэффициента отражения при увеличении скорости
увеличиваются: а – 
; б – 
;
в – 
, однако, по-видимому, такое их поведение
с эффектом вторичной модуляции не связано, а обусловлено повышением степени
неоднородности структуры из-за увеличения разности скоростей волны в
соседствующих участках.
16. Влияние диссипации на вторичную модуляцию
Рассмотрим теперь ту же
ситуацию несколько подробнее, в первую очередь при наличии затухания волны,
которое учтем путем введения мнимой добавки к волновому числу, подобно (20),
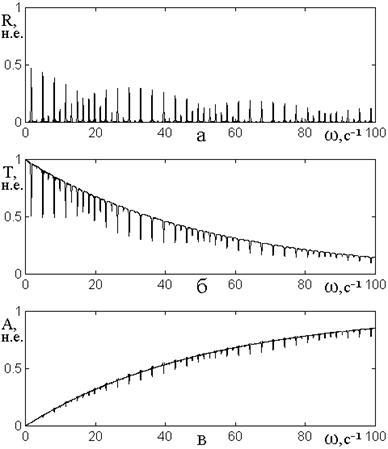
для чего обратимся к рис.12, где показаны зависимости коэффициентов отражения (а), прохождения (б)
и поглощения (в) от частоты 
при
наличии затухания, задаваемого мнимой частью волнового числа, вне барьеров: 
, внутри: 
.
Из рис.12а видно, что
огибающая зависимости коэффициента отражения от
частоты по мере ее увеличения плавно спадает с осцилляциями синусоидального
характера.
Коэффициент прохождения (рис.12б) также плавно спадает, однако теперь
осцилляции проявляются только на его нижней огибающей, тогда как верхняя
спадает монотонно.
Коэффициент поглощения (рис.12в) по мере роста частоты увеличивается
без каких-либо осцилляций, однако на частотах, соответствующих максимумам
отражения и минимумам прохождения, претерпевает небольшие выбросы, составляющие
не более от текущей величины. Амплитуда этих выбросов
также осциллирует, однако ввиду малости осцилляций, эффект вторичной модуляции
здесь проявляется значительно слабее, чем на коэффициентах отражения и
прохождения.
Рис.12. Зависимости коэффициентов отражения (а), прохождения (б) и поглощения (в) от частоты при наличии затухания. Структура – та же, что на рис.8.
Скорость вне барьеров: . Скорость внутри барьеров: 
. Остальные параметры – те же, что на
рис.10.
17. Возможная причина вторичной модуляции
Причина вторичной модуляции, по-видимому, связана с тем, что в структуре барьеры и промежутки между ними представляют собой ограниченные с двух сторон участки однородной среды, то есть обладают определенными резонансными свойствами. Поскольку имеются только два вида таких участков, то и резонансных частот получается всего две. Таким образом, волна распространяется через цепочку распределенных резонаторов, частоты которых чередуются. Такое распространение приводит к биению между этими частотами, в результате чего появляется разностная частота с периодом значительно большим чем исходные. Этот период и проявляет себя в периодическом изменении амплитуды пиков, то есть вторичной модуляции частотной зависимости коэффициента отражения. При увеличении разности между частотами составляющих структуру резонаторов (то есть между значениями скоростей в них) частота биений увеличивается, в результате чего период вторичной модуляции уменьшается, как это и видно из рис.9.
18. Обобщение на случай электромагнитных волн
Проведенное рассмотрение выполнено на примере одномерной волны, как наиболее простой, однако не представляет труда обобщить предложенный способ расчета на случай волн другой природы, в частности, электромагнитных, например как это сделано в работах [19,20]. Так, для случая нормального падения волны достаточно во всех выражениях, кроме показателей экспонент, заменить волновые числа величинами, обратными соответствующим импедансам:
где:
-
импеданс пустого пространства, а 
и 
– магнитная и диэлектрическая проницаемости
-го слоя.
В случае наклонного
падения сначала надо найти углы падения волн обоих направлений во всех слоях
структуры. Эти углы в крайних слоях структуры считаются заданными: 
и 
.
Остальные углы 
между направлением распространения
волны в слое и осью определяются
законом Снеллиуса. Для волн, распространяющихся в положительном направлении оси
, начиная с и , увеличивая индекс на единицу, последовательно
получаем:
Для волн, распространяющихся в
отрицательном направлении оси , начиная с и ,
уменьшая индекс на единицу, последовательно получаем:
После того, как все углы найдены, в случае волн с продольной
поляризацией для волновых чисел надо произвести замену:
при этом экспоненты преобразуются как:
а амплитуды определяются выражениями:
Для волн с поперечной поляризацией замена волновых чисел имеет вид:
экспоненты преобразуются в соответствии
с формулой (26), а амплитуды и 
остаются без изменений:
19. Электромагнитная волна в проводящей среде
В случае одномерной волны
основной ее характеристикой, отражающей свойства среды, является волновое
число. Для электромагнитной волны параметрами среды являются диэлектрическая и
магнитная проницаемости 
и 
, а также проводимость 
. Рассмотрим, как выражаются приведенные
замены переменных через эти параметры. Для простоты дальнейшей записи соответствующий
номеру среды индекс «» будем опускать.
При записи уравнений электродинамики для проводящей среды ее проводимость, удобно включить в диэлектрическую проницаемость в виде мнимой добавки [30,31]:
где 
–
действительная часть волнового числа.
При этом полное волновое число приобретает вид:
Преобразуем эту формулу с помощью известного соотношения для извлечения квадратного корня из комплексного числа [32]:
В результате, подобно (20), получаем:
где:
Именно в таком виде
волновое число надо подставлять в показатель экспоненты, входящий в формулы для
(7). В результате для случая нормального
падения волны получаем:
где и 
соответствуют выражениям (34) и (35),
определяемым через параметры материала для каждой среды.
Для случаев наклонного падения с продольной и поперечной поляризациями вместо (36) получаем:
где угол 
определяется
для каждой среды в соответствии с законом Снеллиуса (23) или (24).
Входящие в формулы (1)-(2)
амплитуды 
,
и 
,
преобразуются
в соответствии с формулами (27) или (29).
Общий вид остальных функций (3)-(6), а также (8)-(11) не меняется, кроме того, что в функциях (4) и (6) производится замена волнового числа на импеданс соответствующей среды:
В среде с проводимостью импеданс становится комплексным. Так, из общего определения импеданса («характеристического волнового сопротивления среды») [30,33] с учетом (30) получаем:
откуда, выделяя действительную и мнимую части и пользуясь (32), получаем:
где:
Из сопоставлеия с (34)-(35) можно видеть, что имеют место соотношения:
а также:
Приведенные соотношения позволяют обобщить все описанные результаты в применении к электромагнитным волнам, распространяющимся в среде с магнитной и диэлектрической проницаемостями, а также проводимостью.
Заключение
Рассмотрена задача о распространении волн через многослойную структуру, содержащую барьерные и периодические неоднородности. Рассмотрение проведено методом исключения. Получены частотные зависимости коэффициентов отражения, прохождения и поглощения.
Показано, что при действительном волновом числе все упомянутые зависимости имеют осциллирующий периодический вид. В случае комплексного волнового числа при небольшой величине мнимой части по сравнению с действительной с увеличением частоты амплитуда осцилляций спадает, а поглощение постепенно растет. При средней величине мнимой части осцилляции почти пропадают и поглощение начинает преобладать над отражением, а при достаточно большой величине мнимой части осцилляции пропадают полностью и отражение преобладает над поглощением.
При действительном волновом числе зависимость коэффициента отражения от частоты при любом количестве, длине и расстоянии между барьерами является периодической. Величина периода соответствует частоте, при которой половина длины волны на этой частоте равняется длине элементарного барьера. Зависимость коэффициента отражения от частоты имеет многолепестковый вид, напоминающий синусоиду с переменной амплитудой. Внутри каждого периода лепестки располагаются симметрично относительно центра периода. Полное количество лепестков на длине периода равно отношению полной длины неоднородности к длине элементарного барьера.
Рассмотрено распространение волны в структуре с периодической неоднородностью на модели многобарьерной среды. Показано, что зависимость коэффициента отражения от частоты имеет те же основные свойства, что и при произвольном сочетании барьеров. Благодаря периодичности структуры внутри каждого периода значительно выделяется центральный лепесток, приходящийся на середину периода, причем с увеличением количества барьеров ширина этого лепестка значительно уменьшается, а амплитуды боковых лепестков резко падают. При увеличении числа барьеров центральная частота главного лепестка несколько увеличивается, его ширина уменьшается, а амплитуда увеличивается, причем эти изменения происходят тем сильнее чем соотношение скоростей внутри и вне барьера больше.
При комплексном волновом числе с увеличением частоты коэффициенты отражения и прохождения уменьшаются, а коэффициент поглощения увеличивается. Показано, что такое изменение происходит при значительно меньшей величине мнимой части волнового числа, чем при одном барьере, что обусловлено накоплением затухания волны при прохождении многих барьеров.
Рассмотрен эффект вторичной модуляции, состоящий в периодическом изменении величины коэффициента отражения по частоте. Показано, что период вторичной модуляции при увеличении различия между параметрами барьеров и промежутков между ними уменьшается. Для интерпретации эффекта высказана гипотеза о многорезонаторном характере распространения волны и связанными с этими резонаторами биениями.
Показана возможность и даны рекомендации для обобщения полученных результатов на случай электромагнитных волн, распространяющихся в проводящей среде с магнитной и диэлектрической проницаемостями.
Работа выполнена при финансовой поддержке за счет гранта Российского Научного Фонда (проект № 14-22-00279).
Литература
1. Бреховских Л.М. Волны в слоистых средах. М.: Наука. 1973.
2. Бреховских Л.М., Годин О.А. Акустика слоистых сред. М.: Наука. 1989.
3. Розенберг Г.В. Оптика тонкослойных покрытий. М.: Гос.изд.физ-мат.лит. 1958.
4. Кизель В.А. Отражение света. М.: Наука. 1973.
5. Oksanen M.I., Hanninen J., Tretyakov S.A. // IEEE Proc.H. 1991. V.138. №7. P.513.
6. Шварцбург А.Б. // УФН. 2000. Т.170. №12. С.1297.
7. Бриллюэн Л., Пароди М. Распространение волн в периодических структурах. М.: ИЛ. 1959.
8. Кирюхин Н.Н., Лисовский Ф.В. // ФТТ. 1968. Т.10. №3. С.709.
9. Зубков В.И., Моносов Я.А., Щеглов В.И. // Письма в ЖЭТФ. 1971. Т.13. №5. С.229.
10. Медников А.М., Никитов С.А., Попков А.Ф. // ФТТ. 1982. Т.24. №10. С.3008.
11. Герус С.В., Харитонов В.Д. // ФММ. 1984. Т.58. №6. С.1069.
12. Вороненко А.В., Герус С.В., Харитонов В.Д. // Изв. ВУЗов. Физика. 1988. Т.31. №11. С.76.
13. Анненков А.Ю., Герус С.В. // РЭ. 1996. Т.41. №2. С.216.
14. Бутько Л.Н., Бучельников В.Д., Бычков И.В., Шавров В.Г. // Журнал радиоэлектроники [электронный журнал]. 2007. №3. URL:
http://jre.cplire.ru/jre/mar07/3/text.html
15. Уиттекер Э.Т., Ватсон Д.Н. Курс современного анализа. Ч.2. М.: ИЛ. 1963.
16. Мак-Лахлан Н.В. Теория и приложения функций Матье. М.: ИЛ. 1953.
17. Флюгге З. Задачи по квантовой механике. Т.1. М.: МИР. 1974.
18. Борн М., Вольф Э. Основы оптики. М.: Наука. 1970.
19. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры. Часть первая. Прямой метод. Сыктывкар: ИПО СыктГУ. 2011.
20. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2010. Т.55. №2. С.133.
21. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры. Часть вторая. Метод матрицы. Сыктывкар: ИПО СыктГУ. 2012.
22. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры. Часть третья. Метод импеданса. Сыктывкар: ИПО СыктГУ. 2012.
23. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры. Часть четвертая. Специфические методы. Сыктывкар: ИПО СыктГУ. 2013.
24. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2012. Т.57. №1. С.67.
25. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2013. Т.58. №1. С.16.
26. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Журнал радиоэлектроники [электронный журнал]. 2013. №1. URL:
http://jre.cplire.ru/jre/jan13/11/text.pdf
27. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры. Часть пятая. Алгоритмические методы. Сыктывкар: ИПО СыктГУ. 2014.
28. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // Журнал радиоэлектроники [электронный журнал]. 2013. №4. URL:
http://jre.cplire.ru/jre/apr13/6/text.pdf
29. Антонец И.В., Шавров В.Г., Щеглов В.И. // Сборник трудов XXI Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2013. С.145.
30. Никольский В.В, Никольская Т.И. Электродинамика и распространение радиоволн. М.: Наука. 1989.
31. Левич В.Г. Курс теоретической физики. Т.1. М.: Наука. 1969.
32. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука. 1973.
33. Красюк Н.П., Дымович Н.Д. Электродинамика и распространение радиоволн. М.: Высшая школа. 1974.