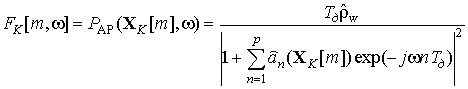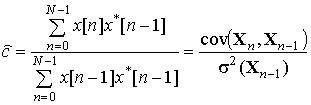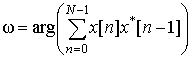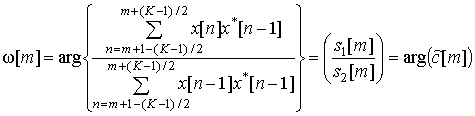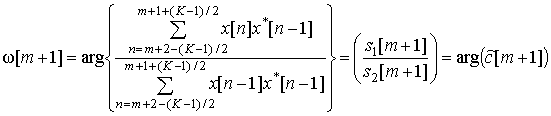УДК 621.396.96
БЫСТРЫЙ АЛГОРИТМ ПАРАМЕТРИЧЕСКОГО ЧАСТОТНО-ВРЕМЕННОГО ОЦЕНИВАНИЯ ОДНОМОДОВЫХ
КОМПЛЕКСНЫХ СИГНАЛОВ
В. Г. Волков 1, Ю. Н. Кривов 2, В. М. Комаров3 , И. В. Лукьянов 3
1 ООО
«НПП «ЛАМА», г. Рыбинск
2 Ярославское высшее
зенитное ракетное училище противовоздушной обороны
3 ФГБОУ ВПО «Рыбинский
государственный авиационный технический университет имени
П. А. Соловьева»
Статья поступила в редакцию 15 ноября 2015 г., после доработки – 13 января 2016 г.
Аннотация. Проводится обзор известных методов частотно-временного оценивания сигналов. Рассматривается быстрый алгоритм частотно-временного оценивания одномодового комплексного сигнала. Приводятся результаты моделирования рассмотренного алгоритма, проводится сравнение с алгоритмом оконного преобразования Фурье и нижней границей Крамера-Рао для оценки параметров ЛЧМ сигнала.
Ключевые слова: частотно-временное оценивание, оконное преобразование Фурье, параметрическое оценивание, ЛЧМ, граница Крамера-Рао.
Abstract. A review of known time-frequency estimation methods is presented. We consider a fast time-frequency estimation algorithm of single-tone complex signal. The results of the simulation algorithm are presented, the comparison with the Short-time Fourier transform and Cramer-Rao lower bound is carried out for chirp signal parameters estimation.
Keywords: time-frequency estimation, Short-time Fourier transform, parametric estimation, chirp, Cramer-Rao lower bound.
Введение
Одной из важных задач при анализе характеристик нестационарных сигналов является построение оценок частотно-временных распределений – зависимости частотных параметров от времени [1–8]. Существует ряд методов для оценки таких распределений: оконное преобразование Фурье (ОПФ), вейвлет-преобразование, распределение Вигнера-Вилля [1–5], метод эмпирической модовой декомпозиции в сочетании с преобразованием Гильберта-Хуанга [7, 8], построение параметрических частотно-временных распределений [9–11].
Каждый из этих методов обладает рядом особенностей. Так, ОПФ обладает всеми особенностями БПФ – расширением частотного спектра для гармонических сигналов с частотами не кратными частотным дискретам БПФ, смещением оценок при уменьшении длины выборки. Вейвлеты позволяют получить хорошую время-частотную локализацию для многих важных приложений в обработке сигналов. Однако, базисные вейвлет-функции, адекватно отражающие частоты гармонических составляющих, сходны с базисными функциями ОПФ и не дают существенного преимущества в части точности оценки частоты. Кроме того, для анализа узкополосных сигналов (а к таким задачам относится оценка несущих частот) и Фурье- и вейвлет- базисы избыточны, требуют большого объема памяти и существенных вычислительных затрат. К недостаткам преобразования Вигнера-Вилля можно отнести интерференции, обусловленные квадратичными свойствами этого преобразования, появление ложных пиков на частотно-временной плоскости, ухудшение разрешения при применении процедур сглаживания, необходимость вычисления БПФ [1, 4]. Метод эмпирической модовой декомпозиции (ЭМД) в сочетании с преобразованием Гильберта-Хуанга не содержит избыточного базиса, однако для построения эмпирических мод используются трудоемкие вычислительные процедуры, ограничивающие его применение в системах реального времени [7, 8].
Параметрические методы [9] построения частотно-временных распределений [3, 4, 10] представляют интерес по следующим причинам:
- для выборок ограниченного объема методы данной группы могут давать лучшие результаты по спектральному разрешению, чем рассмотренные выше [9];
- для параметрических авторегрессионных (далее АР) методов базис разложения заранее не задан, а точность оценки частоты определяется корректностью выбранной модели, длиной выборки и отношением сигнал/шум (ОСШ).
Отметим, что максимально правдоподобной [12] оценкой (МП-оценкой) частоты является периодограммная оценка [13]. В частности для оценки частоты сигнала с одной спектральной составляющей данная оценка имеет вид [13, 14]
где ![]() – периодограмма
сигнала.
– периодограмма
сигнала.
На практике при оценке частоты сигналов с ограниченным набором данных вычисление периодограммы осуществляется при помощи БПФ с использованием известной процедуры дополнения нулями до заданного дискрета БПФ, что влечет за собой дополнительные вычислительные затраты. Для низких порядков АР-моделей существует возможность найти некоторый компромисс между точностью оценки и вычислительной сложностью, используемых алгоритмов. Этим компромиссом является использование АР-оценок, что подтверждается результатами моделирования, представленными в [11].
Параметрические частотно-временные распределения
Для анализа частотно-временных распределений (ЧВР) сигналов с ограниченным набором спектральных составляющих и хорошо согласующихся с АР-моделью сигнала возможно использование параметрического частотно-временного распределения (ПЧВР) или параметрической спектрограммы
где ![]() –
спектральная оценка, полученная одним из известных методов авторегрессионного
спектрального оценивания [9] над данными
–
спектральная оценка, полученная одним из известных методов авторегрессионного
спектрального оценивания [9] над данными ![]() ,
выделенными скользящим окном длительностью K отсчетов;
,
выделенными скользящим окном длительностью K отсчетов;
![]() –
оценка АР-параметра, запись
–
оценка АР-параметра, запись![]() означает, что АР-параметр
вычислен по данным
означает, что АР-параметр
вычислен по данным ![]() ;
;
p – порядок АР-модели;
![]() –
интервал дискретизации сигнала;
–
интервал дискретизации сигнала;
m – сдвиг во временной области;
![]() –
угловая частота;
–
угловая частота;
![]() –
вектор комплексных отсчетов, получаемый из входного вектора
–
вектор комплексных отсчетов, получаемый из входного вектора ![]() посредством скользящего окна
длительностью K, сдвиг m соответствует центральному отсчету
вектора
посредством скользящего окна
длительностью K, сдвиг m соответствует центральному отсчету
вектора ![]() . Вектор
. Вектор ![]() имеет
вид:
имеет
вид:
Идея параметрической
спектрограммы аналогична идее оконного преобразования Фурье: исходная выборка
обрабатывается скользящим окном шириной K отсчетов, в пределах этого окна вычисляются
спектральные оценки с помощью АР-методов [9]. Присутствующее в формуле (1)
дискретное преобразование Фурье можно исключить, используя тот факт, что для
оценки частот сигнала и соответствующих им амплитуд могут быть использованы
аргументы и модули корней ![]() характеристического полинома:
характеристического полинома:
 .
.
Каждому сдвигу m
скользящего окна можно поставить в соответствие множество картежей I = {I1,
I2, …, Ip}, где In = {![]() ,
, ![]() },
}, ![]() – оценка частоты
n-комплексной экспоненты,
– оценка частоты
n-комплексной экспоненты, ![]() – оценка мощности n-комплексной
экспоненты. Тогда ПЧВР можно представить в матричном виде
– оценка мощности n-комплексной
экспоненты. Тогда ПЧВР можно представить в матричном виде
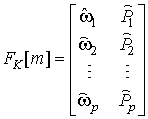 ,
,
где
![]() ;
;
![]() ;
;
arg – функция взятия аргумента комплексного числа.
Параметрические частотно-временные распределения на основе АР-модели первого порядка для одномодовых сигналов
Под одномодовым сигналом будем понимать сигнал, математическая модель которого представима в виде [1, 7, 8]:
где t – время;
A – амплитуда;
f(t) – функция мгновенной частоты;
![]() –
начальная фаза.
–
начальная фаза.
Одной из распространенных задач при анализе радиосигналов является отслеживание закона изменения несущей частоты f(t) в выражении (3). Поскольку в ряде случаев, например, для сигналов с линейной частотной модуляцией (ЛЧМ), скорость изменения мгновенной частоты мала, допустимо разбиение исходного сигнала на достаточно короткие временные интервалы и описание каждого интервала гармонической моделью сигнала. Математическая модель несущего колебания на выходе квадратурного приемника после гетеродинирования представляет собой комплексную экспоненту. Известно [9, 12], что модель комплексной экспоненты может быть описана формирующим фильтром первого порядка
![]() ,
,
где ![]() – АР-параметр;
– АР-параметр;
![]() ;
;
![]() –
интервал дискретизации.
–
интервал дискретизации.
Несложно показать, что оптимальной с точки зрения метода наименьших квадратов оценкой АР-параметра является оценка вида
где N – число отсчетов в выборке;
![]() –
выборочный коэффициент ковариации исходной выборки и выборки сдвинутой на один
отсчет;
–
выборочный коэффициент ковариации исходной выборки и выборки сдвинутой на один
отсчет;
![]() –
выборочная дисперсия исходной выборки;
–
выборочная дисперсия исходной выборки;
* – знак комплексного сопряжения.
Поскольку выборочная дисперсия
![]() в выражении (4) является нормирующей
величиной и влияет лишь на оценку коэффициента затухания комплексной экспоненты,
оценка частоты может быть получена в виде
в выражении (4) является нормирующей
величиной и влияет лишь на оценку коэффициента затухания комплексной экспоненты,
оценка частоты может быть получена в виде
где arg – функция взятия аргумента комплексного числа.
Оценка частоты по формуле (5) представлена в работах [15, 16]. В многочисленных работах (например, [14, 17, 18]) проводятся исследования и предлагаются модификации данной оценки. Модификации обычно сводятся к использованию некоторых взвешивающих функций при вычислении оценок по формуле (5) и процедур фильтрации, что улучшает статистическую устойчивость оценки.
В некоторых случаях использование
немодифицированной формы (5) представляется более интересным. Это связано с тем,
что на основе выражений (4) и (5), можно построить вычислительно-эффективные
алгоритмы оценки частотно-временных распределений. Однако, стоит отметить факт
низкой эффективности данной оценки для значений аргумента в окрестностях,
кратных ![]() , поскольку оценка частоты меняется скачкообразно
в силу свойств функции арктангенса.
, поскольку оценка частоты меняется скачкообразно
в силу свойств функции арктангенса.
Положим K нечетным, тогда согласно формулам (2, 4) оценка частоты на m-шаге может быть получена как
а на m+1 шаге
Заметим, что
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() .
.
Для удобства изменим
порядок индексов в (6) и (7). Для этого введем переменную l = m + (K–1) / 2 с индексацией ![]() по l.
Тогда выражения (6, 7) можно преобразовать к виду
по l.
Тогда выражения (6, 7) можно преобразовать к виду
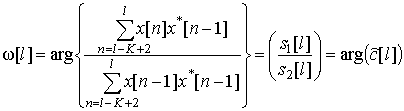 ,
,
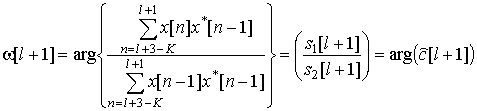
где l = {K, K+1, …, N}.
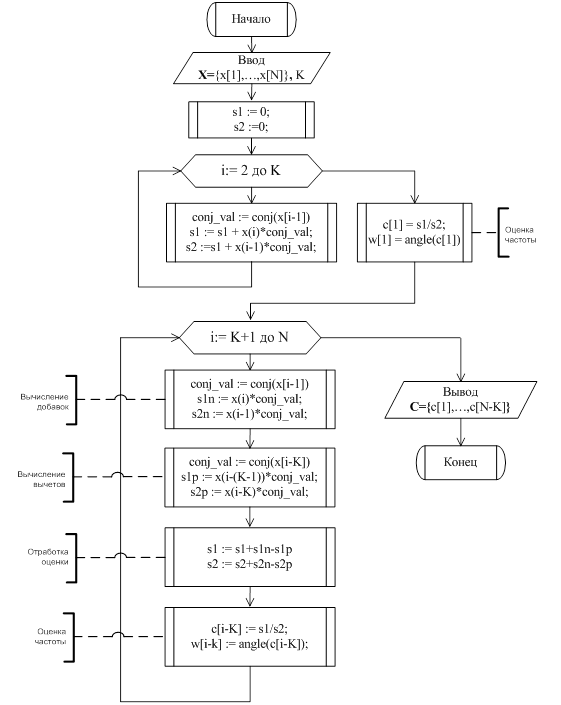
Рисунок 1 – Блок-схема быстрого алгоритма вычисления ПЧВР
комплексной экспоненты
с оптимизацией по использованию памяти
С учетом (8,
9) быстрый
алгоритм можно представить блок-схемой, приведенной на рисунке 1. При этом
существует возможность уменьшения числа комплексных умножений, поскольку
произведения, представляющие «добавки» и «вычеты» в выражениях (8,
9)
вычисляются дважды: на m-ой итерации в качестве «добавок» и на (m+K–1)-ой
итерации в качестве «вычетов». Введя пару циклических буферов для временного
хранения в них «добавок», вычисляемых по формулам (8,
9), можно сократить количество
комплексных умножений на ![]() .
.

Рисунок 2 – Блок-схема быстрого алгоритма вычисления ПЧВР
комплексной экспоненты
с оптимизацией по числу комплексных умножений
Блок-схема алгоритма вычисления ПЧВР с оптимизацией по количеству умножений представлена на рисунке 2. Этот алгоритм может быть эффективно реализован в последовательном виде в устройствах обработки сигналов в реальном времени.
Необходимо отметить, что
представленные алгоритмы позволяют проводить одновременную оценку АР-параметра ![]() и частоту сигнала
и частоту сигнала ![]() . Когда требуется оценка только частоты, вычисления по формуле (9) можно опустить,
приняв делитель
. Когда требуется оценка только частоты, вычисления по формуле (9) можно опустить,
приняв делитель ![]() равным единице.
равным единице.
Отметим, что рекуррентные соотношения (8), (9) в общем случае обладают крайне нежелательным свойством – неустойчивостью, что определяет ограниченность их применения в практических приложениях. Неустойчивость данных соотношений может проявляться для сигналов, отличающихся от принятой модели данных, с низким отношением сигнал шум, с высокой скоростью изменения мгновенной частоты. По этим причинам могут потребоваться дополнительные процедуры обработки исходных данных.
Результаты моделирования
Рассмотрим возможности практического применения предложенного выше алгоритма. На рисунке 3 представлена осциллограмма комплексной огибающей радиосигнала с импульсной модуляцией, оцифрованной с частотой дискретизации 1 ГГц.

Рисунок 3 – Осциллограммы комплексной огибающей
исходного сигнала
с импульсной модуляцией
По осциллограмме видно, что в сигнале присутствует некоторая паразитная частотная модуляция. На рисунке 4,а представлена спектрограмма этого же сигнала, полученная с помощью ОПФ с шириной окна Хемминга 1024 отсчета без перекрытия и с добавлением нулей до 131072 отсчетов, а на рисунке 4,б – результат наложения ПЧВР на спектрограмму рисунка 4,а. ПЧВР выполнено с параметром K = 1024 (белая линия). С помощью спектрограммы, изображенной на рисунке 4,а можно обнаружить некоторую нестабильность частоты в пачках сигнала. При этом идентификация закона изменения частоты затруднительна, поскольку имеет место известное «растекание» спектра при вычислении БПФ. Однако, представленное на рисунке 4,б частотно-временное распределение более чётко локализует частоту сигнала (белая линия) и позволяет сделать вывод, что частота сигнала изменяется по некоторому гармоническому закону.
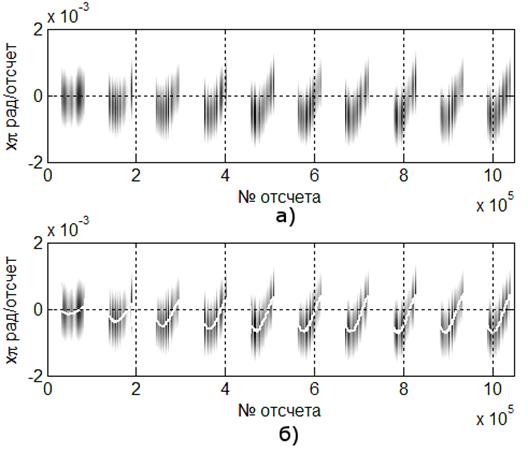
Рисунок 4 – Частотно-временное распределение
а) ОПФ с окном Хемминга 1024 отсчета, Nfft = 131072
б) ОПФ с окном Хемминга 1024 отсчета + ПЧВР (К = 1024)
Стоит отметить, что результаты ОПФ можно представить в более чёткой форме, подобно результатам ПЧВР – с помощью кривой. Для этого при построении частотно-временного распределения используются лишь спектральные отсчеты с максимальной энергией, согласно (0). Однако в этом случае оценка частоты при малом числе отсчетов БПФ может оказаться смещенной, а процедура дополнения нулями требует дополнительных вычислительных затрат. Продемонстрируем данное обстоятельство, решив задачу оценки параметров ЛЧМ сигнала, относящегося к классу одномодовых сигналов в соответствии с определением (3).
Математическая модель ЛЧМ сигнала, получаемого после оцифровки комплексной огибающей, может быть описана следующим выражением
где A – амплитуда сигнала;
n – номер отсчета, n = 0, 1, N–1;
![]() – значение несущей
частоты в начале периода времени формирования;
– значение несущей
частоты в начале периода времени формирования;
b – коэффициент, характеризующий скорость изменения несущей частоты;
![]() – начальная фаза
сигнала;
– начальная фаза
сигнала;
![]() –
аддитивный белый гауссовский шум с дисперсией
–
аддитивный белый гауссовский шум с дисперсией ![]() .
.
Рассчитаем
границы Крамера-Рао (ГКР) для параметров A, f, b
и ![]() . Составим информационную матрицу Фишера
согласно [12]
. Составим информационную матрицу Фишера
согласно [12]
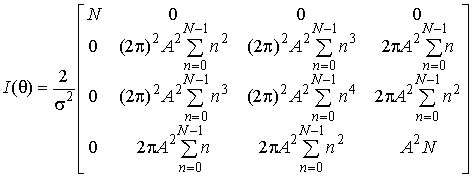
Найдя обратную матрицу ![]() и воспользовавшись формулами Фаулхабера [19],
получим нижнюю границу Крамера-Рао для всех неизвестных параметров в выражении
(10)
и воспользовавшись формулами Фаулхабера [19],
получим нижнюю границу Крамера-Рао для всех неизвестных параметров в выражении
(10)
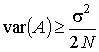 ;
; 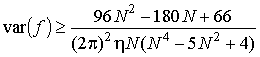 ;
;
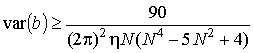 ;
; 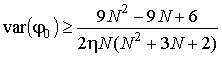 ,
,
где 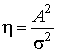 – отношение сигнал/шум.
– отношение сигнал/шум.
Проведем оценку параметров f и b. Для этого оценим
частотно-временное распределение ![]() , после чего построим уравнение
линейной регрессии
, после чего построим уравнение
линейной регрессии ![]() и оценим параметры
и оценим параметры ![]() и
и ![]() с помощью метода наименьших квадратов.
с помощью метода наименьших квадратов.
Для построения оценки
частотно-временного распределения ![]() воспользуемся рассмотренным в данной
статье алгоритмом ПЧВР и алгоритмом оценки частот по максимумам ОПФ. Для лучшей
временной локализации сдвиг окна ОПФ будем выполнять на один отсчет. Для уменьшения
смещения оценки частоты воспользуемся процедурой дополнения нулями до различных
значений Nfft.
воспользуемся рассмотренным в данной
статье алгоритмом ПЧВР и алгоритмом оценки частот по максимумам ОПФ. Для лучшей
временной локализации сдвиг окна ОПФ будем выполнять на один отсчет. Для уменьшения
смещения оценки частоты воспользуемся процедурой дополнения нулями до различных
значений Nfft.
На рисунках 5–13 представлены зависимости среднеквадратической ошибки оценок параметров ЛЧМ, выраженной в дБ, полученные в результате численного эксперимента по формуле
где 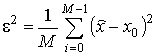 ;
;
![]() – оценка параметра ЛЧМ;
– оценка параметра ЛЧМ;
![]() –
номинальное значение параметра ЛЧМ;
–
номинальное значение параметра ЛЧМ;
M – число экспериментов, для фиксированного ОСШ.
Общее число отсчетов в выборке N = 512, M = 1000.
Так же на этих рисунках приведена граница Крамера-Рао, выраженная в дБ. Необходимо отметить, что сравнение полученных оценок с границей Крамера-Рао [12, 20] не является в полной мере математически строгим. Это связано с тем, что данные оценки являются смещенными (по причине ограниченного размера выборки). Кроме этого оценка среднеквадратической ошибки (11) не является выборочной оценкой дисперсии в чистом виде. Несмотря на это, такая практика сравнения оценок с ГКР широко применяется (например, в [16–18]). В действительности выражение (11) характеризует как выборочную дисперсию, так и смещение оценки.
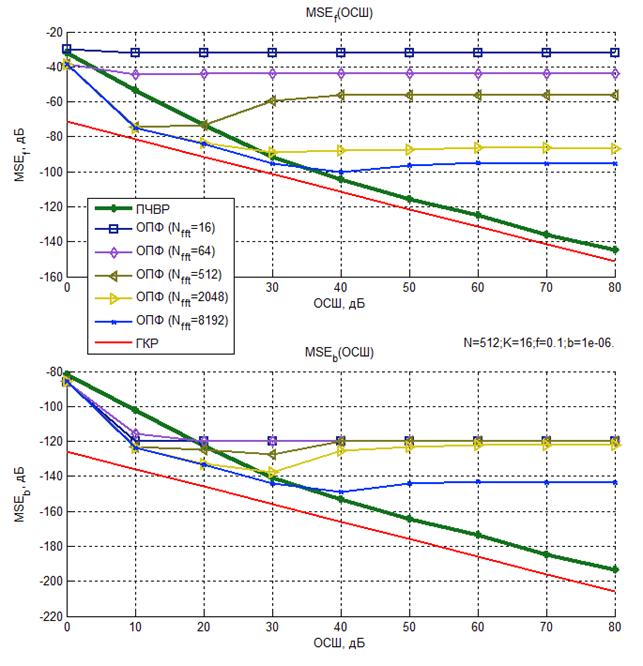
Рисунок 5 – Зависимость среднего квадрата ошибки оценки
параметров ![]() и b
и b
ЛЧМ сигнала от ОСШ (N=512, K=16, f = 0,1, b = 10-6)

Рисунок 6 – Зависимость среднего квадрата ошибки
оценки параметров ![]() и b
и b
ЛЧМ сигнала от ОСШ (N=512, K=32, f = 0,1, b = 10-6)
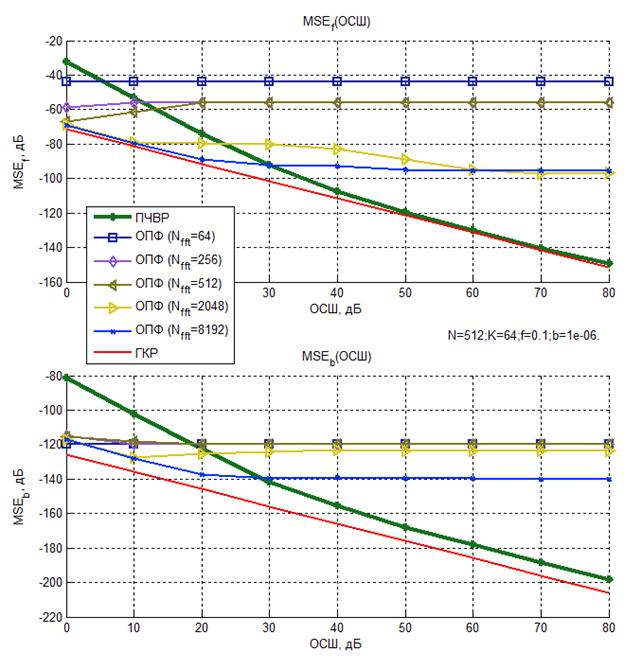
Рисунок 7– Зависимость среднего квадрата ошибки оценки
параметров ![]() и b
и b
ЛЧМ сигнала от ОСШ (N=512, K=64, f = 0,1, b = 10-6)
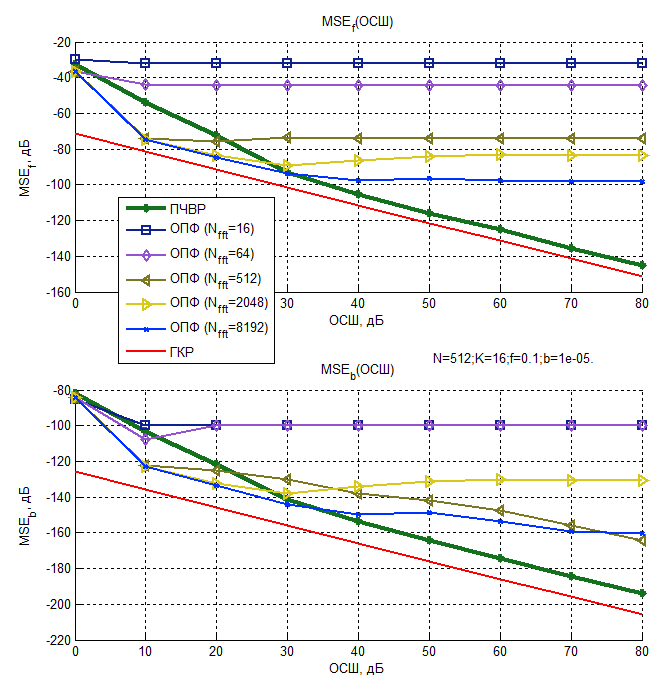
Рисунок 8 – Зависимость среднего квадрата ошибки
оценки параметров ![]() и b
и b
ЛЧМ сигнала от ОСШ (N=512, K=16, f = 0,1, b = 10-5)
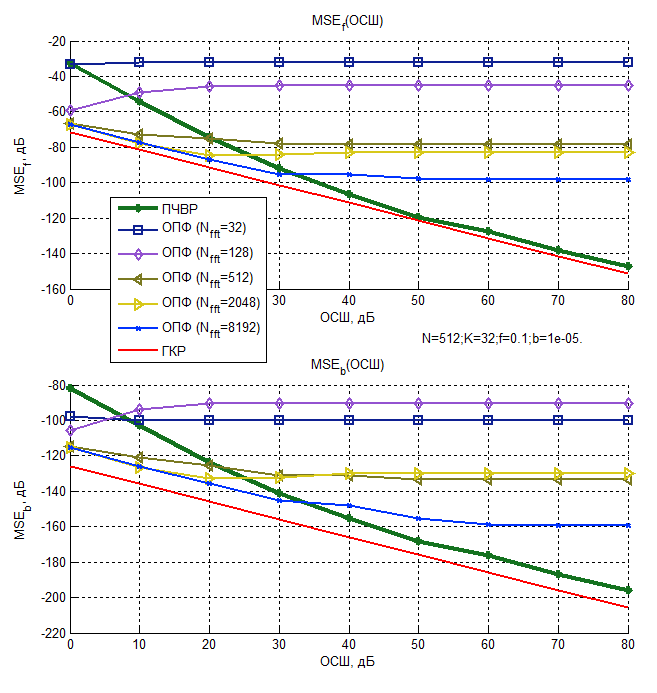
Рисунок 9 – Зависимость среднего квадрата ошибки
оценки параметров ![]() и b
и b
ЛЧМ сигнала от ОСШ (N=512, K=32, f = 0,1, b = 10-5)
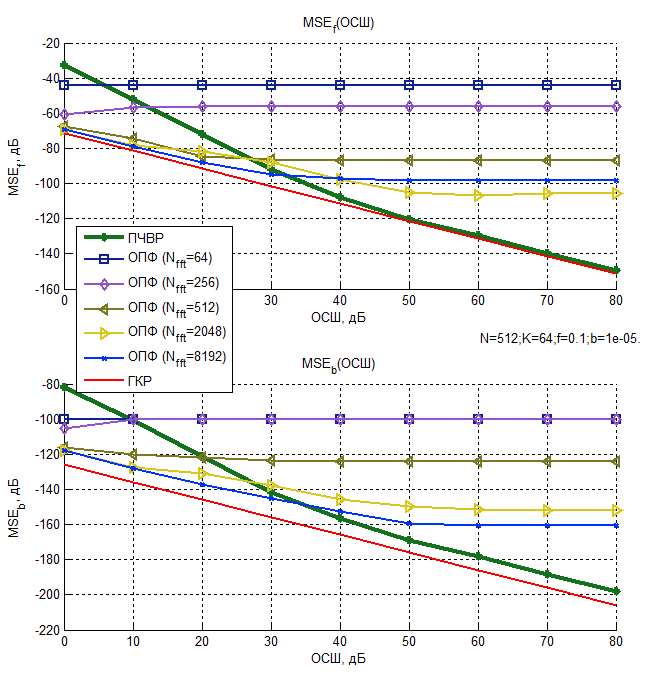
Рисунок 10 – Зависимость среднего квадрата ошибки
оценки параметров ![]() и b
и b
ЛЧМ сигнала от ОСШ (N=512, K=64, f = 0,1, b = 10-5)
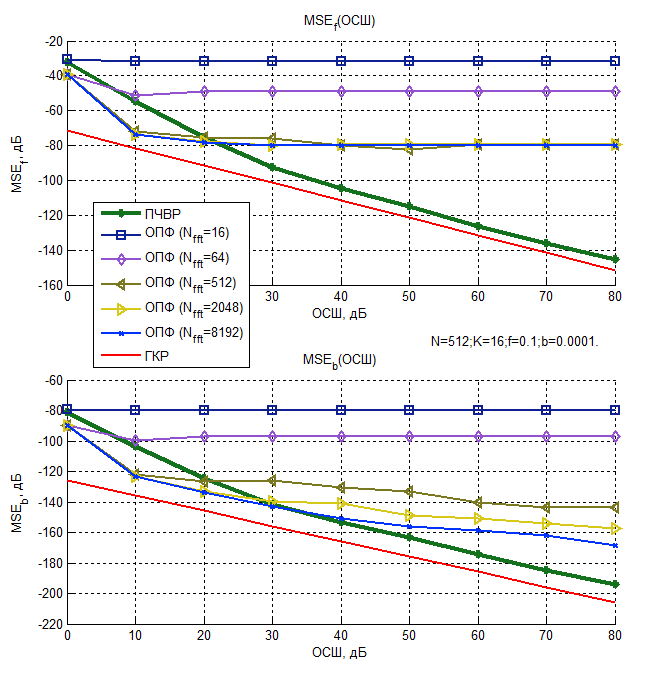
Рисунок 11 – Зависимость среднего квадрата ошибки
оценки параметров ![]() и b
и b
ЛЧМ сигнала от ОСШ (N=512, K=16, f = 0,1, b = 10-4)

Рисунок 12 – Зависимость среднего квадрата ошибки
оценки параметров ![]() и b
и b
ЛЧМ сигнала от ОСШ (N=512, K=32, f = 0,1, b = 10-4)
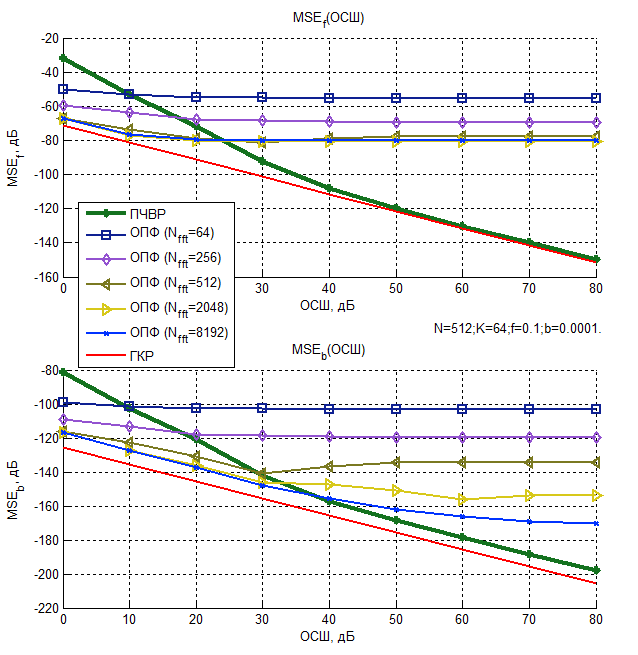
Рисунок 13 – Зависимость среднего квадрата ошибки
оценки параметров ![]() и b
и b
ЛЧМ сигнала от ОСШ (N=512, K=64, f = 0,1, b = 10-4)
Из представленных графиков следует, что при малых Nfft средние квадраты ошибок оценок, использующих ОПФ, практически не зависят от ОСШ и определяются частотным шагом используемого преобразования, а, следовательно, основной вклад в выражение (11) вносит смещение оценки. С увеличением Nfft средние квадраты ошибок оценок, полученных с помощью ОПФ, снижаются, а при малых ОСШ оказываются меньше, чем у метода ПЧВР.
Однако, при высоких значениях ОСШ средние квадраты ошибок оценок, полученных с помощью ПЧВР для параметра f, приближаются к нижней границе Крамера-Рао и демонстрируют наилучшие результаты.
Все рассмотренные методы не являются эффективными для оценки параметра b, при малом числе отсчетов, поскольку они не достигают границы Крамера-Рао. Тем не менее, при высоких ОСШ наиболее точным из них является метод ПЧВР, что является приемлемым для ряда прикладных задач.
Кроме того, метод ПЧВР показывает наилучшее быстродействие, что отображено в таблице 1.
Поскольку рассмотренный метод предназначен для анализа относительно узкополосных сигналов существует возможность значительного увеличения ОСШ за счет адаптивных процедур полосовой или низкочастотной фильтрации.
Таблица 1.Сравнение вычислительной сложности ОПФ и ПЧВР одномодового сигнала
|
Используемый метод |
Оценка числа операций |
Используемая память |
|
ПЧВР (Рисунок 1) |
O(4(2N–K–1)) |
N |
|
ПЧВР (Рисунок 2) |
O(2(3N–K–2)) |
N + K |
|
ОПФ (с временным шагом K отсчетов) |
O((N/K)Nfftlog2Nfft) |
2Nfft |
|
ОПФ (с временным шагом 1 отсчет) |
O((N–K)Nfftlog2Nfft) |
2Nfft |
Заключение
В статье рассмотрен быстрый алгоритм оценки частотно-временного распределения (ПЧВР) одномодового комплексного сигнала.
1. Алгоритм обладает линейной зависимостью вычислительной сложности от количества отсчетов исходного сигнала, что даёт ему преимущество над другими методами при использовании в системах обработки сигнала в реальном времени и в системах, чувствительных к времени выполнения.
2. Наилучшие результаты данный алгоритм демонстрирует при ОСШ больших 30 дБ, что приемлемо для ряда прикладных задач.
3. При высоких значениях ОСШ оценки, полученные методом ПЧВР, приближаются к границе Крамера-Рао.
4. Для уменьшения ошибки оценки частоты при низких значениях ОСШ требуются дополнительные процедуры адаптивной фильтрации.
Литература
1. Малла С. Вэйвлеты в обработке сигналов: Пер. с англ. М.: Мир, 2005. 671 с.
2. L. Cohen, "Time–Frequency Analysis," Prentice-Hall, New York, 1995. ISBN 978-0135945322
3. S. Elouaham, R. Latif, A. Dliou, M. LAABOUBI, F. M. R. Maoulainie, Parametric and Non Parametric Time-Frequency Analysis of Biomedical Signals. International Journal of Advanced Computer Science and Applications, Vol. 4, No.1, 2013
4. Лупов С. Ю. Частотно-временной анализ интерферометрических данных о газодинамических процессах. Специальность 01.04.03 – радиофизика. Диссертация на соискание учёной степени кандидата физико-математических наук. Нижний Новгород, 2012
5. В.И. Кривошеев. Модификация преобразования Вигнера–Вилля для анализа интерферометрических данных газодинамических процессов, Нижегородский госуниверситет им. Н.И. Лобачевского. Радиофизические измерения. Вестник Нижегородского университета им. Н. А. Лобачевского, 2011, № 5(3), с.109–117.
6. M. Ronkin, E. Khrestina, A. Kalmikov. Frequency Estimation for Short Realization of Radar Signals: The New Algorithm Presentation
[Электронный ресурс] // Hikari Ltd [сайт]. URL: http://www.m-hikari.com/ces/ces2014/ces33-36-2014/khrestinaCES33-36-2014-1.pdf (дата обращения 10.04.2015).
7. N. E. Huang et al., “The Empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis,” in Proc. Royal Society London A, vol. 454, pp. 903-995, 1998.
8. Долгих Л. А. Алгоритмы обработки информации на основе анализа быстропеременных процессов. Диссертация на соискание ученой степени кандидата технических наук. Пенза, 2014 г.
9. Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения: Пер. с англ. М.: Мир, 1990. 604 с.
10. Zbigniew Leonowicz. Parametric methods for time–frequency analysis of electric signals. Politechnika Wrocławska. Wroclaw University of Technology, Poland, 2006
11. И. В. Лукьянов. «Параметрическое оценивание несущей частоты коротких радиосигналов» Современная наука. Актуальные проблемы теории и практики. Серия Естественные и Технические Науки Выпуск № 03-04 2015, стр. 11–17.
12. Kay S.M. Fundamentals of Statistical Signal Processing: Estimation Theory (v.1). Prentice Hall, Upper Sadle River, NJ, 1998. 595 p.
13. D. C. Rife and R. R. Boorstyn, “Single-tone parameter estimation from discrete-time observations,” IEEE Trans. Inform. Theory, vol. IT–20, pp. 591–598, Sept. 1974.
14. Vaughan Clarkson. Efficient single frequency estimators. In Proc. Internat. Sympos. Signal Process. Appl., pages 327-330, August 1992.
15. G. W. Lank, I. S. Reed, and G. E. Pollon, “A semicoherent detection and doppler estimation statistic”, IEEE Transactions on Aerospace and Electronic Systems, vol. AES–9, pp. 151–165, Mar. 1973.
16. S. Kay, “A Fast and Accurate Single Frequency Estimator,” IEEE Trans. Acoustics Speech Signal Processing, vol. 37, no. 12, pp. 1987–1990, Dec. 1989.
17. Naveed R. Butt, Andreas Jakobsson, and Magnus Mossberg. Computationally efficient online phase-based frequency estimation of a single tone. 17th European Signal Processing Conference (EUSIPCO 2009) Glasgow, Scotland, August 24-28, 2009
18. Hing Cheung So and Hongqing Liu. Improved Single-Tone Frequency Estimation by Averaging and Weighted Linear Prediction, ETRI Journal, Volume 33, Number 1, February 2011
19. Beardon, A. F. (1996). "Sums of Powers of Integers". American Mathematical Monthly 103. pp. 201–213.
20. Крянев А. В., Лукин Г. В. Математические методы обработки неопределенных данных. М:ФИЗМАТЛИТ, 2003 – 216 с.