УДК 621.396.1

ДИАГНОСТИКА АПЕРТУРНЫХ РАСПРЕДЕЛЕНИЙ АНТЕНН ПУТЕМ ИЗМЕРЕНИЙ В ЗОНЕ БЛИЖНЕГО ИЗЛУЧЕННОГО ПОЛЯ

 

И. Ю. Данилов, Ю. Е. Седельников

Казанский национальный исследовательский технический университет им. А.Н. Туполева – КАИ

 

Статья поступила в редакцию 27 августа 2015 г., после доработки – 14 января 2016 г.

 

Аннотация. Рассматривается задача нахождения апертурного распределения антенны по данным измерений в области ближнего излученного поля. Рассмотрено  два подхода: метод восстановления и метод фокусировки. Обсуждаются особенности указанных методов, анализируется  точность определения. Показано, что метод фокусировки имеет ряд достоинств и может обеспечивать точность, приемлемую для практических приложений.

Ключевые слова: апертурное распределение, метод измерений в ближнем поле, метод восстановления, сфокусированная антенна, точность измерений.

Abstract. The problem of finding the antenna aperture field distribution by measurements in the area of near radiated field is searched. Two approaches: the reduction  and the focusing methods are considered. The features of these methods as well as accuracy aspect are analyzed. It is shown that the focusing method has several advantages and can provide accuracy acceptable for practical applications.

Key words: aperture distribution, the method of measurement in the near field, the method of recovery, focusing antenna, measurement precision.

 

Введение

Диагностике антенн уделяется большое внимание на  всех этапах жизненного цикла современных антенных систем. Несмотря на значительные достижения, актуальность диагностики антенн не ослабевает, особенно в связи с использованием в современных антенных системах АФАР, гибридно-зеркальных антенн, а также технологий конформных антенных решеток.

Для указанных  целей предложено, разработано и находит применение большое число различных приемов. Во-первых, это непосредственные измерения амплитудно-фазовых распределений (АФР) в раскрыве антенны. Известно большое число  способов измерения указанных величин, и устройств для их реализации. Сколь-нибудь полный перечень их привести здесь не представляется возможным. Примерами могут служить Патенты РФ и АС СССР:   № 2267795, 2254585, 2275644, 1786453, 1770918, 1693568, 15997788, , 1223170, 1229644, 1146611, 1415203 и др.

Непосредственное измерение  электромагнитных полей вблизи антенны  не всегда  позволяет решать задачи диагностики апертурных распределений. Не останавливаясь детально на обсуждении высказанного положения, отметим  лишь то, что в ряде практически важных случаев проведение  указанных измерений непосредственно в апертуре или хотя бы на малом расстоянии от антенны технически неосуществимо. Для этих случаев предложены  приемы, имеющие в основе измерения параметров электромагнитного поля антенны в ближней зоне излучения антенны  с последующим определением искомого АФР путем некоторой обработки данных измерений. Стоит особо отметить, что в настоящее время указанные принципы измерений все более завоевывают позиции на практике.  Сегодня хорошо развиты не только методы нахождения диаграмм направленности в дальней зоне, но и соответствующие программно- аппаратные средства [2,3,9,10]. Представляет несомненный интерес разработка технологий измерений, осуществляемых в ближней зоне излучения для диагностики апертурных распределений  различных антенн, в том числе АФАР.

Методы определения  внешних характеристик антенн по данным измерений в ближней зоне к настоящему времени  хорошо изучены [1-4] и реализованы в промышленных измерительных комплексах [5-6]. Не обойдены вниманием  также вопросы определения характеристик антенн по данным измерений, осуществляемым  в зоне Френеля [7].

Задача нахождения  амплитудно-фазовых распределений по данным измерений создаваемых антенной электромагнитных полей в ближней зоне также нашла отражение в ряде работ [8-16]. Не останавливаясь подробнее на деталях, отметим, что в основу большинства из них составляет  два подхода. Первый из них -  использование процедуры восстановления АФР антенны по данным измерений. В этих случаях решаемая задача может быть представлена следующим образом. Пусть известна функциональная связь исходного АФР и измеренного поля в ближней зоне излучения:   – апертурное распределение в области , а создаваемое им электромагнитное поле в области   – . Связь их значений описывается линейным оператором :

                                                              (1)

Для антенных решеток с числом элементов   или непрерывных апертур при соответствующей дискретизации функции и рассмотрении значений электромагнитного поля в конечном  числе точек области  оператор   - прямоугольная матрица размерности . Способы решения задач, описываемых уравнением (1), хорошо известны. Так при использовании  критерия минимума среднеквадратического отклонения решение основано на  использовании  псевдообратной матрицы [17]:

                                                   (2)

где   - транспонированная и комплексно сопряженная матрица .

 Второй подход можно обосновать различным образом. Так, если считать матрицу   достаточно близкой к диагональной, решение (2) принимает вид:

.                                                    (3)

В работе [11] показано, что к аналогичному представлению приводит представление оператора задачи на основе приближения стационарной фазы. Можно указать и на физическую трактовку решений типа (3), использованную на техническом уровне в [15].

Действительно, область измерений может рассматриваться как виртуальная  приемная антенна с синтезированной апертурой. Ею с учетом соответствующей фазировки «сигналов», соответствующих каждому из положений измерительной антенны-зонда, осуществляется избирательный прием излучения обследуемой антенны, относящийся к  определенному участку ее апертуры. Для этого фазы принятых сигналов должны быть сдвинуты таким образом, чтобы обеспечить синфазное сложение колебаний, соответствующих излучению выделенного  участка апертуры. Нетрудно увидеть, что с учетом некоторой коррекции значений амплитуд суммируемых сигналов  это соответствует алгоритму обработки (3). Таким образом, эффективность определения АФР по измеренным значениям излучаемого поля методом фокусировки непосредственным образом зависит от реализации фокусирующих свойств в зоне ближнего излученного поля. Очевидно, что «фокусировка» согласно (3) не является единственно возможным вариантом и можно рассчитывать на  улучшение качества определения АФР за счет  модификации алгоритма (3).

Целесообразность поиска вариантов совершенствования метода фокусировки связана еще и со следующим обстоятельством. Не требует доказательств тот факт, что в идеальных условиях метод  фокусировки уступает   по потенциальной  точности определения искомого АФР решению обратной задачи.  Не стоит, однако, упускать из вида и то, что для решения  задачи восстановления (2) требуется совершение нескольких  операций с матрицами, включая обращение, что при больших их размерностях может вызвать  определенные затруднения. Кроме того, наличие в алгоритме процедуры обращения матриц более остро ставит вопрос о требуемой  точности исходных данных, включая оператор задачи и измеренные значения параметров излученного поля. Метод фокусировки имеет в этом отношении явное преимущество. Поэтому, несмотря на ряд выполненных работ, отмеченных выше, вопрос об использовании метода фокусировки не стоит считать закрытым. В статье рассматриваются возможности улучшения точностных показателей указанного метода.

1. Метод фокусировки в задачах нахождения апертурного АФР

Выше уже отмечалось, что в задаче нахождения  апертурного распределения по данным измерений в ближней зоне  излучения физической интерпретацией метода фокусировки является  последовательное осуществление избирательного приема излучения обследуемой  антенны виртуальной антенной решеткой, сфокусированной в режиме приема в заданную точку (реально – участок конечных размеров)  ее апертуры. Для более наглядного представления существа возможных модификаций этого метода целесообразно рассмотреть еще одно представление. В силу принципа взаимности определение искомого АФР можно осуществить путем  приема обследуемой антенной излучения виртуальной антенной решеткой, фокусируемой последовательно в различные точки ее апертуры. Рис. 2  иллюстрирует этот факт  для случая измерений дискретной антенны.

          Указанное представление наглядно показывает   пути улучшения точностных показателей метода фокусировки. Действительно, в этом случае коэффициент передачи участка «вход виртуальной решетки - выход обследуемой антенны» будет пропорциональным значениям свертки функций апертурного АФР и сфокусированного поля виртуальной решетки. Отсюда, в частности, следует, что точное воспроизведение функции апертурного АФР возможно только, если распределение сфокусированного поля имеет вид δ–функции, что физически неосуществимо.

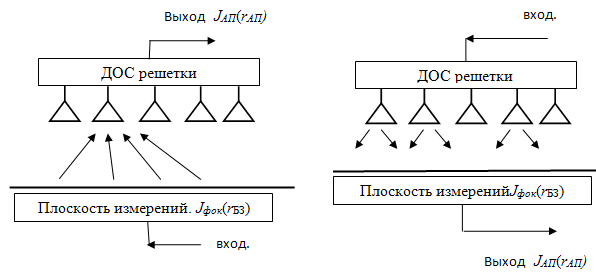
а)                                                         б)

Рис. 1. К определению апертурного распределения  антенной решетки методом фокусировки приемной  системы.
а) область измерений как передающая антенна,   б) виртуальная фокусировка в режиме приема.

 

Это же означает, что приближенное  воспроизведение искомой функции апертурного распределения будет тем более точным, чем меньше значения размеров сфокусированной области и ниже уровень боковых лепестков. Таким образом,  возможности улучшения точностных показателей метода фокусировки непосредственным образом связаны с формирование сфокусированных полей в зоне с указанными свойствами.

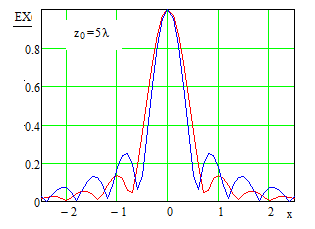
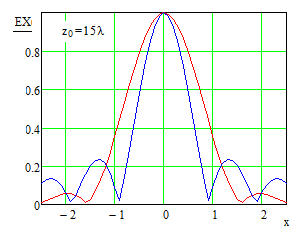
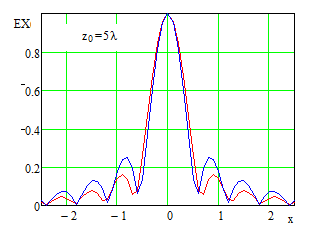
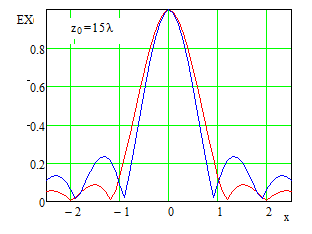
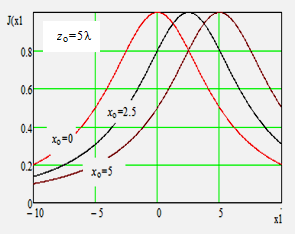
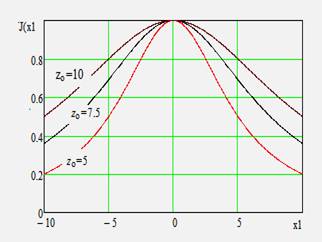
В плоскости, параллельной апертуре и отстоящей от нее на расстояние, равное фокусному расстоянию, интенсивность сфокусированного поля имеет характер выраженного «пика», окруженного всплесками меньшей интенсивности, аналогичным боковым лепесткам ДН антенны в дальней зоне и имеющих сходную с ними природу (Рис. 2).

 

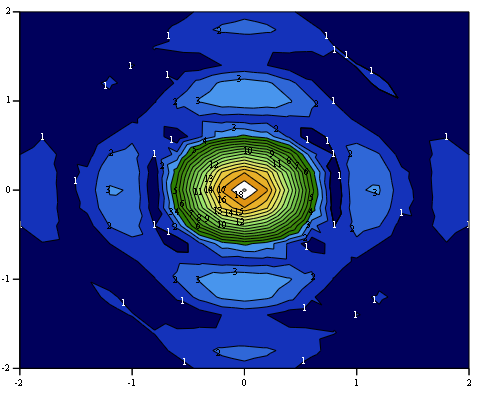
Рис. 2 Распределение горизонтальной составляющей напряженности электрического поля. Размеры сфокусированной апертуры 20λ х 20λ, фокусное расстояние  10λ, амплитудное распределение в соответствие с (3).

 

Свойства электромагнитных полей,  сфокусированных в зоне ближнего излученного поля, в последнее время достаточно активно  изучались. Данные о наиболее важных в практическом плане положениях апертурной теории сфокусированных апертур содержится в [18-22]. Для рассматриваемых приложений наиболее существенно следующее:

- размеры сфокусированной области и значения уровней боковых лепестков характеризуются сложной зависимостью от вида функции амплитудного распределения, фокусного расстояния  и положения точки фокусировки относительно центра сфокусированной апертуры;

- характер этих зависимостей, сохраняя общие черты с аналогичными для полей дальней зоны излучения антенн, имеет в то же время  и ряд достаточно важных отличий. Прежде всего, это относится к наличию явно выраженной зависимости уровней боковых лепестков от величины относительного фокусного расстояния, в том числе тенденцией к их возрастанию по мере уменьшения фокусного расстояния. Иллюстрацией могут служить приведенные на Рис. 3 зависимости напряженности поля в фокальной плоскости, для двух видов амплитудного распределения ,  и:

 

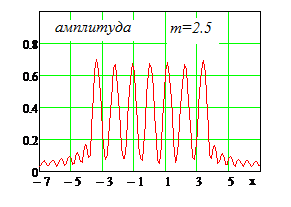
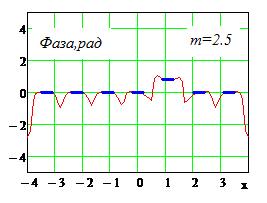
Рис. 3. Нормированная зависимость напряженности горизонтальной составляющей электрического поля  от вида амплитудного  распределения и фокусного расстояниядля  равномерного распределения и  вида косинус в квадрате. Апертура размером 20λ, расстояние по оси абсцисс – в долях длины волны. Синий цвет - рm=1, красный - m=2.5 Синий цвет - равномерное амплитудное распределение, красный – вида «косинус в квадрате».

 

Второй пример – амплитудное распределение вида

 (4)

- условие достижения максимального КНД существенно отличается от случая дальней зоны[1]. В частности, в случае необходимости перемещения   точки фокусировки в фокальной плоскости (сканирование) для достижения максимума КНД требуется осуществлять не только соответствующую фазировку излучателей, но и изменять амплитудное распределение (Рис.5).

 

Рис. 4. Нормированная зависимость напряженности горизонтальной составляющей электрического поля,
слева  от вида амплитудного  распределения и фокусного расстояния.
Синий цвет - m=1, красный - m=2.5, расстояние по оси абсцисс – в долях длины волны.

.

 

Рис. 5 Амплитудные распределения, обеспечивающие максимум КНД в точке фокусировки
при различных ее положениях в фокальной плоскости для квадратной  апертуры размером 20λ.

 

Перечисление этих свойств преследует  единственную цель: показать, что фокусировка, осуществляемая согласно (3), не только не является единственно возможной, но и не может считаться наилучшей в задаче определения АФР по значениям комплексных амплитуд полей, излучаемых в ближней зоне. Действительно, как уже отмечалось выше, качественное  определение АФР по данным измерений в зоне ближнего излученного поля требует обеспечения минимальных значений как размеров сфокусированной области, так  и уровней боковых лепестков. Не трудно увидеть, что если фокусировка осуществляется согласно правилу (3), это означает, что  в виртуальной решетке используется амплитудное распределение вида , где  и – фокусное расстояние и расстояние от - й точки апертуры до точки фокуса с координатами  . Известно [18-19], что данное амплитудное распределение обеспечивает максимально возможный КНД в точке фокуса , но не минимальные значения ширины сфокусированной области и уровней боковых лепестков. Отсюда вытекает и практическое следствие: алгоритм (3) не гарантирует наиболее точного определения АФР антенны по данным измерений ее полей в зоне ближнего излученного поля. Отсюда же вытекает еще одно следствие: при надлежащем  выборе размеров виртуальной антенны, фокусного расстояния и вида дополнительно вводимой весовой функции (т.е. амплитудного распределения сфокусированной виртуальной антенны) можно  надеяться на повышение точности определения искомого АФР антенны.

2. Иллюстрации

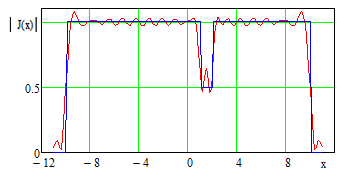
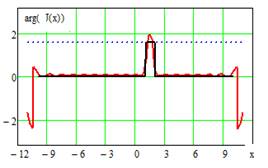
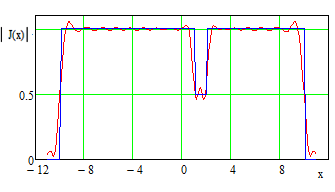
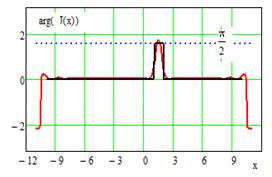
В качестве иллюстрации изложенного выше приводим результаты моделирования процесса определения  АФР антенны по данным измерений в ближней зоне излучения. В качестве первого примера выступает линейная апертура с задаваемым АФР J(x) (Рис. 6).

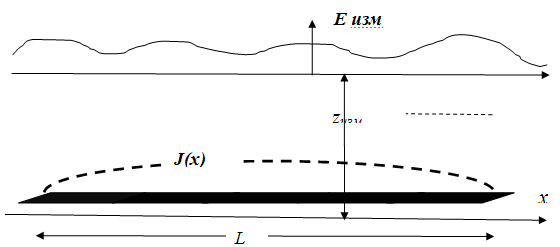
Рис. 6. Модель антенны

 

Процедура моделирования состояла в следующем. По заданным размерам апертуры и АФРJ(x)  рассчитывалось пространственное распределение в зоне ближнего излученного поля . Затем измеренные значения подвергались обработке в соответствие с алгоритмом (3), модифицированным путем введения весовой функции, соответствующей фокусировке виртуальной апертуры в текущую  точку контролируемой антенны согласно приведенным выше соображениям. Расчет  проводился согласно  классическим представлением излучаемого поля заданной системой источников. Наконец, проводилось сравнение исходного АФР и определенного согласно использованной процедуре. Указанный подход часто используется при  моделировании процессов измерений параметров антенн в ближней зоне излучения, например в [19]. На Рис. 7 показаны результаты: исходное АФР  линейной антенны длиной 20λ и «измеренное» на расстоянии z₀=4λ в области длиной 25λ с шагом 0.5λ, на Рис. 8 – найденные АФР при различных параметрах весовой функции вида (4). Приведенный пример наглядно демонстрирует возможность улучшения воспроизведения исходного АФР в модификации метода фокусировки при введении в алгоритм (3) надлежащей  весовой функции.

 

Рис. 7. Исходное АФР и «измеренное» на расстоянии 5λ от апертуры

 

Амплитудное распределение	Фазовое распределение
m=0 Максимальная относительная погрешность  7.9%	m=0 Максимальная погрешность 20.10
m=1 Максимальная относительная погрешность  4.6%	m=1  Максимальная погрешность 13.20
m=2.5   Максимальна относительная погрешность  3.5%	m=2.5  Максимальная погрешность 8.10

 

Рис. 8 Исходное АФР в антенне и найденное по данным измерений  в зоне ближнего излученного поля при различных весовых функциях.

 

Второй пример (Рис. 9) – коллинеарная антенная решетка из 7 полуволновых излучателей с шагом 1.1λ. Амплитудное распределение в элементе – косинусное, в решетке – равномерное. Фаза  возбуждения элемента №1 – 45⁰ , в остальных равна нулю.

 

 

Максимальная относительная погрешность  14.3%	Максимальная погрешность 230
Максимальная относительная погрешность  7.1%	Максимальная погрешность 9.40

 

Рис. 10 Результаты моделирования определения АФР антенны модифицированным методом фокусировки при двух различных весовых функциях.

 

Результаты  нахождения апертурного АФР модифицированным методом фокусировки приведены на Рис. 10. Весовая функция и ее параметры – аналогичны использованным выше. В обоих  примерах весовая функция с параметром  m=1 соответствует известному решению - алгоритму (3).

Приведенные данные моделирования подтверждают  возможность повышения точности определения АФР в антенне  при  модификации метода фокусировки, путем введения  дополнительной весовой функции. Можно ожидать, что   вид оптимальный весовой функции, обеспечивающий максимальную точность определения АФР,  зависит от ряда факторов, в том числе от значения фокусного расстояния и, отчасти, от характера обследуемого АФР. Рассмотрение вопроса об оптимальной  весовой функции, очевидно,  выходит за рамки настоящей работы. Авторы предполагают обсудить эту сторону вопроса в отдельной публикации.

3. Влияние основных видов погрешностей на точность нахождения АФР по данным измерений в зоне ближнего излученного поля

На первый взгляд может сложиться  представление, что решение (2), основанное на обращении оператора , в любом случае обеспечивает достижение  более точных результатов по сравнению с методом фокусировки. Это, безусловно, было бы справедливо, если бы значения оператора задавались точно, а результаты измерений поля в области   не содержали неизбежной составляющей  погрешности. В реальности наличие указанных погрешностей приводит к появлению погрешности определяемых значений апертурного распределения . Это означает, что заключение о преимуществе решения (2) перед (3) уже не является очевидным.  Ниже проводится более детальное рассмотрение этой стороны вопроса. Поскольку провести анализ влияния погрешностей аналитически не представляется возможным, наиболее реалистично прибегнуть к прямому численному моделированию. Вычислительный   эксперимент осуществляется по следующей схеме: задается исходное апертурное распределение  , рассчитывается  «точное» пространственное распределение . Далее имитируется реальное измерение  путем добавление составляющих, соответствующих погрешности измерения . После этого проводится расчет функции АФР по «измеренным» значениям , причем с обязательным учетом того факта, что прямой оператор задачи также задан с погрешностью:  .  При проведении подобных экспериментов, особенно если они имеют предварительный характер, как правило, можно ограничиться  максимально простыми моделями «измеряемых» АФР.

 

3.1. Метод восстановления

Ключевым моментом, во многом определяющим «качество»  восстановления апертурного распределения , является влияние погрешностей исходных данных. Для задач восстановления это:

- погрешности измерения параметров электромагнитного поля в области , обусловленные как условиями проведения измерений, так и свойствами измерительных средств:  ;

- погрешность прямого оператора, связанная с неточным определением его значений в качестве модели антенных измерений: .

С учетом указанных погрешностей найденная функция апертурного распределения будет неизбежно отличаться от истинного значения:

 

        (5)

 

Для оценки меры отличия истинной и восстановленной функций апертурного распределения необходимо, как минимум, ввести в рассмотрение разумные модели погрешностей  и .

Основным фактором, определяющим значения , является погрешность самих измерительных средств, при этом влияние   собственных шумов определяет принципиально неустранимую составляющую общей погрешности.  В соответствии с принятыми представлениями [24]   значения могут рассматриваться как некоррелированные случайные величины с нулевым средним значением и нормальным распределением реальных и мнимых частей.

Задание модели погрешностей прямого оператора т ребует предварительного выявления порождающих их причин. Обычно считают, что измерительный датчик (пробник, измерительная антенна) реагирует на преобладающую компоненту поля, например соответствующую ориентации вектора напряженности электрического поля парциального источника в апертуре антенны. Тогда .  Результат «приема», в силу влияния  неучитываемых компонент в зоне ближнего излученного поля, а также  реальных направленных и поляризационных характеристик  приемного датчика,  будет отличаться от  значений, соответствующих введенной модели. Последнее обстоятельство существенно еще и потому, что аналитическое описание свойств датчика, как правило, не может быть получено в строгом виде.

Это означает, что  значения  коэффициентов  в условиях реальных измерений  отличаются от используемых в апертурной модели. Это становится особенно очевидным, если учесть, что  для их строгого определения нужно учитывать  действительную комплексную векторную диаграмму направленности измерительного датчика.  Последняя, в реальности, зависит от ряда трудно учитываемых факторов, например, дифракции на кромках рупора (открытого конца волновода) и в точности неизвестна.  Таким образом, приходится считаться с тем, что используемый прямой оператор задачи принципиально задан с некоторой погрешностью . Для количественных оценок  влияния указанной погрешности на результат восстановления необходимо ввести в рассмотрение разумную модель .

В основу одного из возможных способов можно положить  следующее. Измеряемое значение интенсивности ЭМП в n-й точке в области , создаваемого m – ым элементом апертуры, представляют собой коэффициент передачи  четырехполюсника со входами, соответствующими  измерительному датчику и элементу апертуры. Для них  проводится по возможности точное электродинамическое моделирование величин . Указанное моделирование можно осуществить с использованием хорошо апробированных программных средств, например, пакета CSTMICROWAVESTUDIO. Результаты сравниваются с расчетными значениями  согласно апертурной модели.

Вычислительные эксперименты, проведенные авторами на этой основе, позволяют составить  модель погрешности прямого оператора. Значения   для каждого m-го элемента  апертуры могут рассматриваться как случайные величины с  нулевым средним значением,  нормальным распределением реальной и мнимой частей и значением СКО, не превышающим  (5…10) процентов  от соответствующих максимальных значений. Радиус корреляции составляет величину порядка (0.5 … 1) длины волны.  Указанные представления  и далее можноиспользовать в качестве модели погрешности задания прямого оператора .

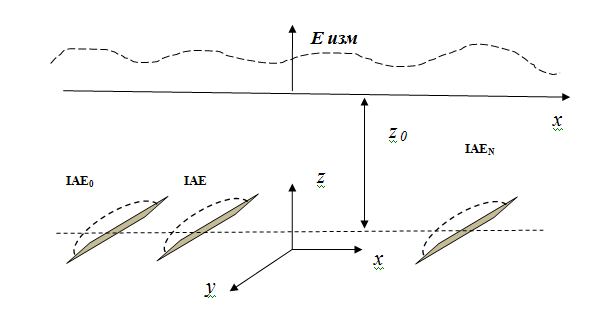
Рис. 11. К оценке влияния погрешностей. Модель антенны

 

В вычислительном эксперименте по оценке влияния  и на точность восстановления использована максимально упрощенная модель антенны в виде линейной решетки излучателей с «измерением» создаваемого ей электромагнитного поля в плоскости апертуры на расстоянии , соизмеримом с протяженностью антенны. Численные расчеты проводились для эквидистантной линейной  антенной решетки из 9 параллельных излучателей, поляризованных перпендикулярно апертуре (Рис. 11).

Исходное амплитудно-фазовое распределение в апертуре показано на Рис. 12, строка 1. «Измерения» осуществлялись вдоль линии, параллельной апертуре на расстоянии 5 длин волн от нее. Электрический размер датчика – 0.5λ, шаг измерений – 0.75λ, число точек «измеряемого»» поля – 30. «Измерения» осуществлялись для различных значений  максимальной относительной  погрешностью δE при максимальной относительной погрешности величин , равных δA . На Рис. 12 приведены результаты моделирования для ряда сочетаний параметров, характеризующих погрешность измерений   и прямого оператора .

 

		Амплитудное распределение			Фазовое распределение
δA=0   δE=0		Максимальная относительная погрешность  0%			Масимальная погрешность 0
δA=0.05   δE=0		Максимальная относительная погрешность  3.6%			Максимальная погрешность 11.40
δA=0   δE=0.05		Максимальная относительная погрешность4.7%			Максимальная погрешность 7.630
δA=0.05   δE=0.05		Максимальная относительная погрешность  6.7%		Максимальная погрешность 15.30.6
.
δA=0.1   δE=0		Максимальная относительная погрешность  5.3%			Максимальная погрешность 30.5.40
δA=0   δE=0.1		Максимальная относительная погрешность  8.3%			Максимальная погрешность 11.40
δA=0.1   δE=0.1		Максимальная относительная погрешность  14%			Максимальная погрешность 32.40
δA=0.15   δE=0		Максимальная относительная погрешность  12.7%			Максимальная погрешность 42.60
δA=0   δE=0.15	Максимальная относительная погрешность  6.7%		Максимальная погрешность 30.60

 

Рис. 12. Исходное и восстановленное  АФР при различных значениях погрешностей  и  δE.
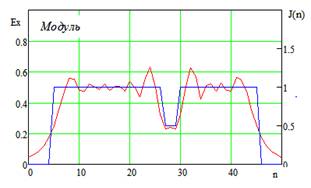
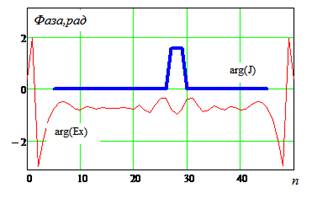
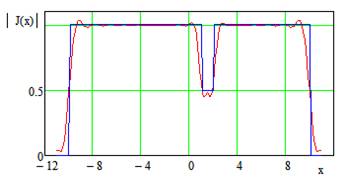
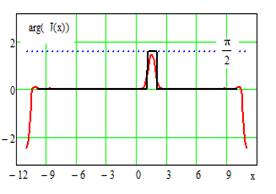
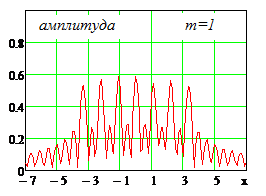
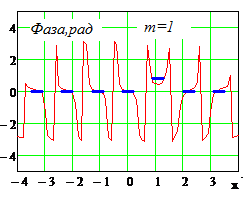
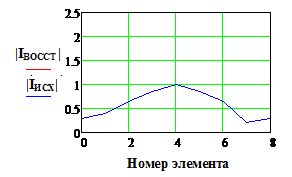
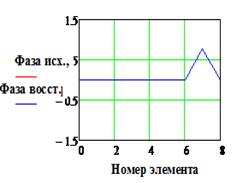
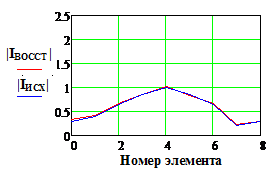
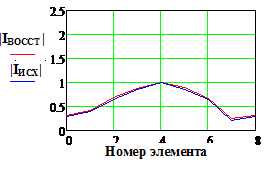
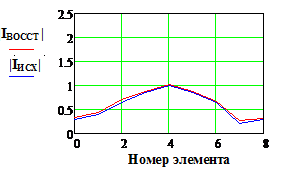
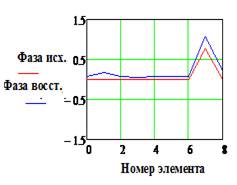
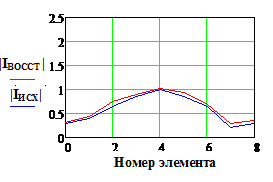
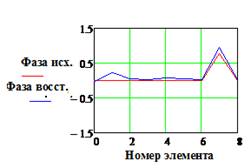
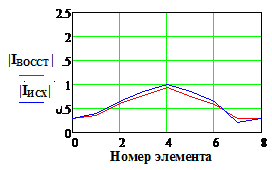
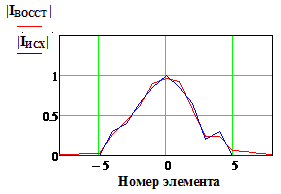
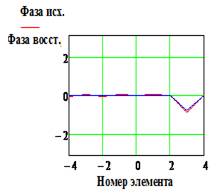
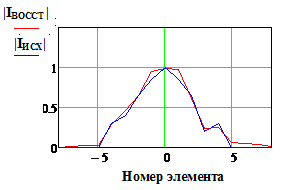
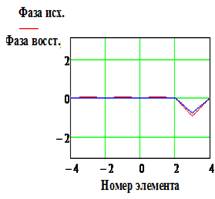
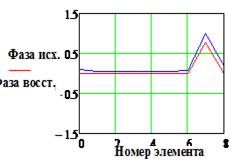
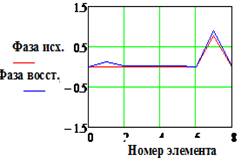
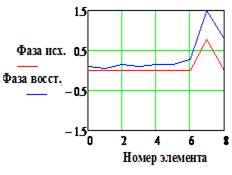
|I_ИСХ| и |I_ВОССТ | и  Фаза исх., и Фаза восст.(рад) - исходное и восстановленное АФР соответственно, k – номер излучателя решетки.

 

Проведенный анализ эффектов влияния погрешностей величин  и  на результат восстановления апертурного распределения показывает следующее:

- влияние погрешностей  и  в наибольшей мере проявляется в снижении  точности восстановления фазового распределения поля в апертуре антенны;

- влияние погрешностей  и  с максимальными значениями порядка 5% и менее практически несущественно (Рис. 11, строки 2-4);

- при значениях погрешностей свыше указанных значений  погрешность восстановления исходного АФР начинает заметным образом возрастать. При этом погрешность элементов матрицы прямого оператора  оказывает более выраженное  влияние;

- при значениях погрешностей прямого оператора и измеренных данных более 10%  «качество» восстановления становится явно недостаточным для типовых практических ситуаций. В частности, максимальное значение погрешности восстановления фазового распределения. Так при значениях =0.1 и 0.15 погрешность достигает 25⁰ и 42^{0 ,} , в то же время максимальная  относительная погрешность восстановления амплитудного распределения не превышает 10%.

3. 2. Метод фокусировки

Как и в варианте использования процедуры восстановления ключевым моментом является количественная мера достижимой  погрешности найденного апертурного распределения. Аналитическая оценка ее  не представляется возможной и единственно реальным также является использование численного моделирования. Для получения сопоставимых результатов численное моделирование, очевидно, должно осуществляться в сходных условиях и с  исходными данными, использованным в предыдущем разделе при оценках точности метода восстановления.

Принципиально важными являются два положения:

- очевидно, что в допущении отсутствия погрешностей метод фокусировки будет уступать по точности методу восстановления. Это обстоятельство можно рассматривать как наличие методической погрешности данного способа;

- второе принципиальное положение состоит в том, что при использовании метода фокусировки отсутствует погрешность задания элементов прямого оператора, неизбежная для метода восстановления. Действительно, измеренные значения  непосредственно используются в процессе фокусировки как амплитудно-фазовое распределение виртуальной сфокусированной антенны. Принципиальное значение имеет   лишь то, что  в результате  измерения величины  определяются с некоторой погрешностью . Кроме того, при этом при осуществлении виртуальной фокусировки согласно правилу (3) или его модификаций не принимается в расчет фактическое отклонение фазовой диаграммы направленности измерительного датчика от постоянной. Однако это может  рассматриваться как составляющая часть общей погрешность . В процессе анализа можно в полной мере воспользоваться модельными представлениями  предыдущего раздела.

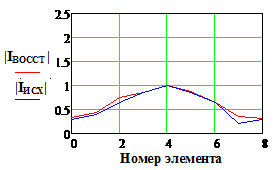
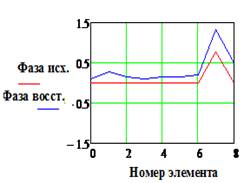
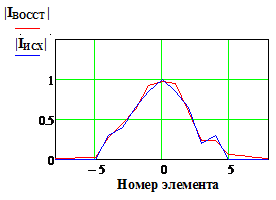
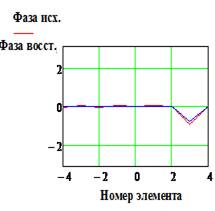
Как и в случае использования метода восстановления, количественные оценки наиболее естественно получить путем прямого численного моделирования. Указанные оценки  для случая определения апертурного распределения в антенне, рассмотренной в предыдущем разделе, приводятся ниже. На Рис. 13 показаны исходное апертурное распределение и найденное модифицированным методом фокусировки с использованием весовой функцией, вида «косинус в квадрате».

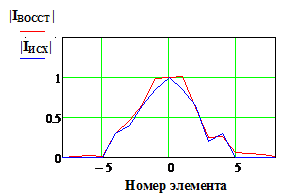
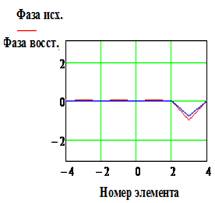
Как и следовало ожидать, в гипотетическом случае - отсутствии погрешностей, метод фокусировки  заметно уступает по точности методу восстановления (Рис 12, верхняя  строка). В то же время при их наличии  погрешность определения апертурного распределения оказывается  зависящей  от погрешности измерения в меньшей мере (Рис. 12). Так при 10…15% точность определения искомого АФР еще остается удовлетворительной.

 

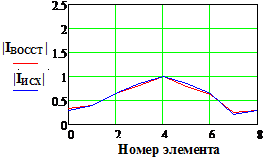
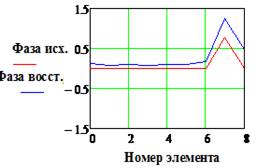
δ =0	Максимальная относительная погрешность  6.1%	Максимальная погрешность 7.60
δ  =0.05	Максимальная относительная погрешность  6.5%	Максимальная погрешность 12.90
δ =0.1	Максимальная относительная погрешность  7%	Максимальная погрешность 15.30
δ =0.15	Максимальная относительная погрешность  7.6%	Максимальная погрешность 18.10

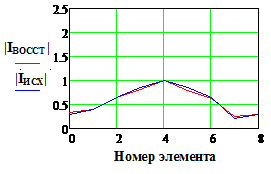
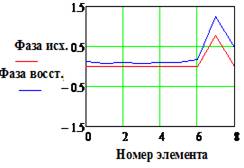
Рис. 13. Исходное и найденное амплитудно-фазовое распределение при различных значениях погрешности измеренных данных.
Размер области измерения - 15λ, фокусное расстояние - 5 λ, весовая функция – косинус в квадрате.
|I_ИСХ| и |I_ВОССТ | и  Фаза исх., и Фаза восст.(рад) - исходное и восстановленное АФР соответственно, k – номер излучателя решетки.

 

Заключение

Из приведенных результатов можно сделать следующие выводы.

1. Определение апертурного  амплитудно-фазового распределение по данным измерений в области ближнего излученного поля методом фокусировки может оказаться достаточно эффективным, несмотря на наличие составляющей методической погрешности по сравнению с методом восстановления.

2. Сравнивая результаты восстановления  апертурного распределения и нахождения его методом фокусировки нетрудно увидеть следующее:

- в отсутствие погрешностей метод фокусировки уступает по точности методу восстановления. В частности, в приведенных примерах относительная погрешность определения АФР  достигала значений  порядка 7% и 3⁰  при нулевых значениях для метода восстановления;

- при наличии погрешностей соизмеримого уровня картина меняется: метод восстановления уже может «проигрывать» по точности методу фокусировки. Так при уровне погрешностей порядка 10% погрешность метода фокусировки составила в проведенных опытах 15.8% и 9.2^0, а для метода восстановления – около 10% и 25⁰ соответственно.

Резюмируя изложенное, можно утверждать, что в задаче определения апертурного распределения по результатам измерений в зоне ближнего излученного поля использование метода фокусировки может быть практически приемлемым по  точности. В то же время требования к вычислительным ресурсам в этом случае значительно меньшие, так как используемые алгоритмы не требуют обращения матриц большой размерности. Для определения оптимальных условий проведения оценки АФР методом фокусировки, включая выбор оптимальных весовых функций,  требуется проведение дополнительной проработки.

       Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации в рамках проектной части государственного задания З.1962.2014/К.

 

Литература

 

1. Yaghijan A.D. An overview of near-field measurements. IEEE Trans. on Ant. and Prop, 1986, v. AP-34, № 1. pp. 30-45

2. Кинбер Б.Е. Теория измерений параметров антенн. В кн.: Обратные задачи теории рассеяния и теория статистически нерегулярных трактов. М, 1979, стр. 142-225

3.  Бахрах Л.Д. , Кременецкий С.Д., Курочкин А.П., Усин В.А., Шифрин Я.С Методы измерений параметров излучающих систем в ближней зоне. Л. Наука 1985 -272с.

4. Воронин Е.Н., Нечаев Е.Е., Шашенков В.Ф. Реконструктивные антенные измерения. М.: Наука, Физматлит, 1995

5.Компания  Agilent Technologies. Испытания антенн http://www.unitest.com/pdf/antenna_measurements_ru.pdf  Дата обращения 21.07.2015

6. Комплекс для измерения параметров антенн в ближней зоне с использованием плоского сканера http://www.trimcom.ru/index.php?level= other_parts_russian&time=1177749492 Дата обращения 21.07.2015

7. Кривошеев Ю.В. Измерение характеристик антенн в зоне Френеля на разреженной сетке углов.  Дисс. на соиск. уч. степ.канд. техн. наук. М.;ОАО «Радиофизика» 2014

8. Гармаш В.Н., Пузанков В.А. Восстановление амплитудно-фазового распределения апертурных антенн по измеренным в ближней зоне полям излучения. Труды МФТИ, вып. 112, 1977 с. 9-14

9.  Кинбер Б.Е.,Антипин Л.П., Мартынов А.Н. О диагностике элементов  ФАР  методом фокусировки «Радиотехника и электроника», 1983, т.28, с.843-853.

10. Борисов С.Ю. Разработка методов, алгоритмов и устройств для определения амплитудно-фазовых распределений и внешних характеристик антенн в амплифазометрическом методе антенных измерений. Дисс.на соиск.уч. степ. канд. техн. наук, М.: МЭИ 1992 г.

11. Коротков В. С. Исследование и разработка методов реконструкции тока по измеренному полю излучающих систем Дисс.на соиск.уч. степ. канд. техн. наук. Горький, 1984 г.

12. Анохина А.Д. , Нечеса А.Е. , Усин В.А. Определение АФР в элементах фазированных антенных решеток по измерениям амплитуды ближнего поля [электронный ресурс].  URL: http://radio.kpi.ua/public/journals/17/preview/1996/S002134701996100081_preview.pdf

13. Нечаев Е.Е.Рождественский И.Н. Экспериментальные исследования по восстановлению фазового распределения поля в раскрыве антенны по данным амплитудных измерений. Научный вестник МГТУ ГА, 2007 г., № 112. - С. 17 – 22

14. Калинин Ю.Н. Измерение диаграмм направленности антенн в планарном сканере без измерения фазы. «Антенны» вып.1 (212), 2015 с. 61-68

15.  Кисмерешкин В.П., Лобова Г.И.Устройство измерения АФР антенны. Патент РФ № 2329518 опубл.20.07.2008

16. Толкачев А.А., Меркулов О.Н. Антипин Д.С. Кувшинов Г.В.и др. Восстановление распределения поля в раскрыве решетки модуляционным способом. Радиотехника и электроника, т.ХХ № 3 1975 с. 617-620 

17. Гантмахер Ф. Р. Теория матриц. — 5-е изд. — М.: ФИЗМАТЛИТ, 2004. — 560 с.

18. Vedenkin D.A., Potapova O.V.Sedelnikov Yu,E.    ANTENNAS, FOCUSED IN THE NEAR  RADIATED FIELD zone. FEATURES AND TECHNICAL АРРLICATIONS Proceedings  of International Conference  on antenna theory and technique  ICATT 13 Odessa, Ukraine 2013 p. 560-565

19. Низамутдинов Р.Р. Сфокусированные антенны в задачах радиоволновой диагностики

Диссертация на соискание ученой степени канд. техн. наук. Казань, КГТУ им А.Н.Туполева, 2011

20  J. Musil  Properties of antennas focused in the Fresnel zone Czechoslovak Journal of Physics.Vol. 17, Number 10, 1967. p 874-888

21.  Седельников Ю.Е., Потапова.О.В.  Коэффициент направленного действия апертурных антенн, сфокусированных в зоне ближнего излученного поля. «Радиотехника»  № 7 2015 с118-123

22.  R. C. Hansen Focal Region Characteristics of Focused Array Antennas.IEEETrans. onAntennas and Propagat.1985. т. AP-33, № 6, с. 1328-1337

23. Шафранов Е.В.  Восстановление характеристик зеркальных антенн по результатам моделирования процесса измерения поля в ближней зоне. Электронный ресурс http://mmp.vestnik.susu.ac.ru/article/ru/49. Дата обращения 02. 09.2015 г

24. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений . 2-е издание. Л.: Энергоатомиздат, 1991 -304с.

---

[1] Определение КНД в зоне ближнего излученного поля дано в  [21].