| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 6, 2001 |  |
ЭФФЕКТИВНОСТЬ ПРИЕМА СИГНАЛОВ НА ФОНЕ КОМБИНИРОВАННОЙ ПОМЕХИ С ДОПОЛНИТЕЛЬНОЙ ОБРАБОТКОЙ В МЕДИАННОМ ФИЛЬТРЕ
Воронежский государственный университет, физический факультет
Получена 4 июня 2001 г.
Рассмотрена задача обнаружения полезного сигнала с неизвестным временным положением на фоне гауссовского шума и импульсной помехи. Предлагается ввести в структуру приемника медианный фильтр, позволяющий существенно ослабить импульсную помеху. Найдены характеристики обнаружения сигнала на фоне комбинированной помехи в случае применения процедуры дополнительной медианной фильтрации.
1. Введение
Цифровые системы связи включают в свою структуру ряд подсистем,
осуществляющих процедуры ожидания вызова, установления связи и вхождения в
синхронизм, приема информационных сообщений и ряд других важных и
вспомогательных операций [1]. Условия работы современных радиосредств таковы,
что в приемнике кроме флуктуационных шумов
![]() и полезного сигнала
и полезного сигнала
![]() присутствует импульсный поток
присутствует импульсный поток
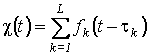 с регулярной или
хаотической структурой
с регулярной или
хаотической структурой
Причиной появления импульсного потока могут быть как
внешние импульсные помехи, так и сбои в работе канального декодера, связанные с
замиранием сигналов в канале связи, перемещением абонентов и так далее.
Необходимо отметить, что временное положение сигнала
![]() в режимах ожидания вызова,
поиска сигнала, вхождения в синхронизм является неизвестным параметром,
определенным внутри априорного интервала поиска с большим числом элементов
разрешения. Прием полезного сигнала в асинхронных системах связи также приводит
к задаче обнаружения (различения) сигналов с неизвестными параметрами.
в режимах ожидания вызова,
поиска сигнала, вхождения в синхронизм является неизвестным параметром,
определенным внутри априорного интервала поиска с большим числом элементов
разрешения. Прием полезного сигнала в асинхронных системах связи также приводит
к задаче обнаружения (различения) сигналов с неизвестными параметрами.
Совокупность гауссовского шума и потока квазидетерминированных импульсов (помехи) будем называть комбинированной помехой. Вопросам построения приемных систем, устойчивых к воздействию импульсной помехи посвящено большое число работ [2, 3] и др. Многочисленные алгоритмы можно разделить на три группы. К первой принадлежат способы борьбы, основанные на ограничении сигналов (схемы типа ШОУ, ШОС) или схемы с ключевыми АРУ. Однако, они применимы только к некоторым типам сигналов, приводят к их искажению, существенно уменьшают отношение сигнал/шум.
Ко второй группе принадлежат адаптивно – компенсационные алгоритмы. Они весьма сложны, работоспособны при очень малом уровне шумов и рассматриваются только в теоретическом плане.
К третьей группе
принадлежат алгоритмы, основанные на непараметрических методах статистики [3],
устойчивые к действию помех. Однако они требуют некоторой обучающей выборки из
ансамбля помех, относительно которой формируется решающая статистика. Причем
элементы выборки из ансамбля помех должны быть независимыми. Применение таких
методов к типичной задаче обнаружения сигнала
![]() с неизвестным временным положением на
интервале, содержащем много элементов разрешения по задержке на фоне
коррелированных шумов, вызывает большие затруднения. Наконец, борьба с комбинированной
помехой может вестись путем применения мощных помехоустойчивых кодов. Однако
этот путь приводит к снижению скорости передачи сообщений и усложнению
структуры приемника.
с неизвестным временным положением на
интервале, содержащем много элементов разрешения по задержке на фоне
коррелированных шумов, вызывает большие затруднения. Наконец, борьба с комбинированной
помехой может вестись путем применения мощных помехоустойчивых кодов. Однако
этот путь приводит к снижению скорости передачи сообщений и усложнению
структуры приемника.
В данной работе
предлагается двухэтапный алгоритм обработки наблюдаемого процесса
![]() . На первом этапе производится медианная
фильтрация, которая с высокой вероятностью позволяет устранить импульсы из
потока
. На первом этапе производится медианная
фильтрация, которая с высокой вероятностью позволяет устранить импульсы из
потока
![]() . После
этого может производиться обработка профильтрованного процесса
. После
этого может производиться обработка профильтрованного процесса
устройством, рассчитанным только на флуктуационную
компоненту
![]() . Структура алгоритма обработки на втором
этапе и работа порогового устройства могут быть оптимизированы с учетом
статистической структуры профильтрованного шума
. Структура алгоритма обработки на втором
этапе и работа порогового устройства могут быть оптимизированы с учетом
статистической структуры профильтрованного шума
![]() , искажений сигнала
, искажений сигнала
![]() и вероятности прохождения
импульсной помехи через медианный фильтр. Поэтому в данной работе получено
достаточно полное статистическое описание профильтрованного ансамбля помех и
разработаны методы расчета характеристик обнаружения сигналов с неизвестными
параметрами на фоне комбинированной помехи.
и вероятности прохождения
импульсной помехи через медианный фильтр. Поэтому в данной работе получено
достаточно полное статистическое описание профильтрованного ансамбля помех и
разработаны методы расчета характеристик обнаружения сигналов с неизвестными
параметрами на фоне комбинированной помехи.
2. Медианная фильтрация входного ансамбля помех
Итак, пусть в течение
времени
![]() на
входе медианного фильтра наблюдается процесс
на
входе медианного фильтра наблюдается процесс
![]() . Шум
. Шум
![]() будем считать гауссовским процессом с
нулевым математическим ожиданием и корреляционной функцией
будем считать гауссовским процессом с
нулевым математическим ожиданием и корреляционной функцией
![]() . Полезный сигнал
. Полезный сигнал
![]() имеет неизвестное временное положение
имеет неизвестное временное положение
![]() , причем на этом интервале содержится много элементов
разрешения по задержке. Поток импульсов
, причем на этом интервале содержится много элементов
разрешения по задержке. Поток импульсов
![]() имеет вид
имеет вид
Здесь
![]() - амплитуда импульса в потоке,
- амплитуда импульса в потоке,
![]() - его неизвестное временное
положение. Множитель
- его неизвестное временное
положение. Множитель
![]() с
вероятностью
с
вероятностью
![]() , и
, и
![]() с вероятностью
с вероятностью
![]() . Такое задание импульсной помехи
соответствует потоку Бернулли [4], для которого на интервале
. Такое задание импульсной помехи
соответствует потоку Бернулли [4], для которого на интервале
![]() имеется не более
имеется не более
![]() точек. Статистика
каждой точки характеризуется парциальной плотностью
точек. Статистика
каждой точки характеризуется парциальной плотностью
![]() . Здесь
. Здесь
![]() - вероятность появления
- вероятность появления
![]() точки,
точки,
![]() - распределение моментов ее появления.
Считается, что
- распределение моментов ее появления.
Считается, что
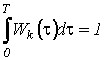 ,
т.е. удовлетворяет условию нормировки.
,
т.е. удовлетворяет условию нормировки.
Если
![]() , то все
, то все
![]() точек всегда присутствуют на интервале
точек всегда присутствуют на интервале
![]() . Если
. Если ![]() , то положение точек
детерминировано. При
, то положение точек
детерминировано. При ![]() и
и
![]() поток является регулярной импульсной
помехой. Если
поток является регулярной импульсной
помехой. Если
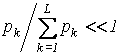 ,
то при достаточно больших, но конечных
,
то при достаточно больших, но конечных
![]() , поток Бернулли приближается по своим
свойствам к потоку Пуассона [4]. Заметим, что пуассоновская аппроксимация
потока при большом числе
, поток Бернулли приближается по своим
свойствам к потоку Пуассона [4]. Заметим, что пуассоновская аппроксимация
потока при большом числе
![]() позволяет упростить расчеты свойств
профильтрованного ансамбля помех. В дальнейшем будет рассматриваться частный
случай потока Бернулли с неперекрывающимися парциальными плотностями, так что
позволяет упростить расчеты свойств
профильтрованного ансамбля помех. В дальнейшем будет рассматриваться частный
случай потока Бернулли с неперекрывающимися парциальными плотностями, так что
![]() , при
, при
![]() . При этом отдельные
импульсы
. При этом отдельные
импульсы
![]() потока
также считаются неперекрывающимися.
потока
также считаются неперекрывающимися.
Пусть из смеси
![]() в дискретные моменты
времени с периодом дискретизации
в дискретные моменты
времени с периодом дискретизации
![]() берутся отсчеты, которые подвергаются
скользящей медианной фильтрации по
берутся отсчеты, которые подвергаются
скользящей медианной фильтрации по
![]() отсчетов. Число
отсчетов. Число
![]() , называемое шириной апертуры
медианного фильтра, для удобства считается нечетным. В таком случае медианой из
, называемое шириной апертуры
медианного фильтра, для удобства считается нечетным. В таком случае медианой из
![]() отсчетов
является отсчет
отсчетов
является отсчет
![]() с
номером
с
номером
![]() в
упорядоченной последовательности
в
упорядоченной последовательности
![]() .
.
Были выбраны медианные фильтры с небольшой апертурой
![]() , содержащей от
, содержащей от
![]() до
до
![]() отсчетов. Такие апертуры обеспечивают
темп обработки в реальном масштабе времени при умеренных требованиях к
быстродействию системы обработки.
отсчетов. Такие апертуры обеспечивают
темп обработки в реальном масштабе времени при умеренных требованиях к
быстродействию системы обработки.
Медианный фильтр
подавляет полностью часть импульсной помехи, если количество импульсов в
пределах апертуры не превосходит
![]() . Используя производящую функцию
. Используя производящую функцию
![]() потока Бернулли [4]
потока Бернулли [4]
где
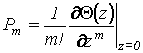 , можно записать вероятность подавления
импульсной помехи как
, можно записать вероятность подавления
импульсной помехи как
Если все
![]() , то для потока Бернулли
, то для потока Бернулли
Для потока Пуассона [4]
В выражении (7)
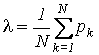 - средняя интенсивность
потока Пуассона в пределах апертуры медианного фильтра, а
- средняя интенсивность
потока Пуассона в пределах апертуры медианного фильтра, а
![]() - временной интервал, на котором
берутся
- временной интервал, на котором
берутся
![]() отсчетов
для медианной фильтрации. Тогда мы имеем
отсчетов
для медианной фильтрации. Тогда мы имеем
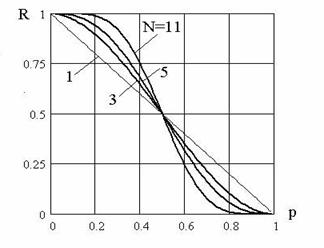
На рис. 1 приведены результаты расчетов по формулам (6) и (8) вероятности подавления импульсной помехи медианным фильтром.
Рис. 1. Зависимость вероятности подавления импульсной помехи медианным фильтром для потоков Бернулли .
Кривые соответствуют различным апертурам медианного
фильтра. Линия, которая соответствует
![]() , соответствует отсутствию медианной
фильтрации.
, соответствует отсутствию медианной
фильтрации.
Был выполнен цикл
статистического моделирования медианной фильтрации потоков Бернулли и Пуассона
с фиксированными и флуктуирующими по закону Рэлея амплитудами. Результаты
моделирования показали их хорошее соответствие расчетным значениям вероятности
подавления
![]() Однако,
для интенсивных потоков происходит не подавление, а усиление и трансформация
его в поток импульсов другой структуры. Например, входной поток может
трансформироваться в поток импульсов со случайной длительностью. Очевидно, что
медианная фильтрация имеет смысл при
Однако,
для интенсивных потоков происходит не подавление, а усиление и трансформация
его в поток импульсов другой структуры. Например, входной поток может
трансформироваться в поток импульсов со случайной длительностью. Очевидно, что
медианная фильтрация имеет смысл при
![]() .
.
Медианная фильтрация является нелинейной операцией над входным процессом, изменяющей статистику принятой реализации. Однако, некоторые теоретические результаты имеются только по статистике профильтрованного белого шума. Аналитический расчет преобразования статистики коррелированных процессов весьма затруднителен из-за неразработанности соответствующего математического аппарата. Поэтому был использован метод математического моделирования процесса медианной фильтрации принятой смеси с последующей аппроксимацией выходных статистических характеристик.
Исследовалась эволюция
первых четырех кумулянтов и корреляционной функции
![]() профильтрованного шума
профильтрованного шума
![]() при обработке
стационарного гауссовского процесса
при обработке
стационарного гауссовского процесса
![]() с нормированной корреляционной функцией
вида
с нормированной корреляционной функцией
вида
![]() и
и
![]() .
.
Результаты зависят от
соотношения ширины спектра
![]() , периода дискретизации
, периода дискретизации
![]() и ширины апертуры
и ширины апертуры
![]() . Исследование
коэффициентов асимметрии и эксцесса процесса
. Исследование
коэффициентов асимметрии и эксцесса процесса
![]() показало их малость даже для небольших
апертур размером
показало их малость даже для небольших
апертур размером
![]() отсчетов.
Поэтому, одномерное распределение профильтрованного шума можно считать
гауссовским.
отсчетов.
Поэтому, одномерное распределение профильтрованного шума можно считать
гауссовским.
Удалось определить, что
корреляционные свойства шума
![]() зависят от параметра
зависят от параметра
![]() [5]. Если
[5]. Если
![]() , то корреляционные
функции
, то корреляционные
функции
![]() и
и
![]() практически совпадают.
Если
практически совпадают.
Если
![]() , то у
процесса
, то у
процесса
![]() ширина
спектра сужается по сравнению с шириной спектра
ширина
спектра сужается по сравнению с шириной спектра
![]() .
.
Моментные функции
определялись путем обработки нескольких десятков реализации
![]() длиной от трех до десяти тысяч
интервалов корреляции. Тем самым устранялось возможное нарушение эргодичности,
связанное с реальным моделированием процессов на основе псевдослучайных
датчиков чисел.
длиной от трех до десяти тысяч
интервалов корреляции. Тем самым устранялось возможное нарушение эргодичности,
связанное с реальным моделированием процессов на основе псевдослучайных
датчиков чисел.
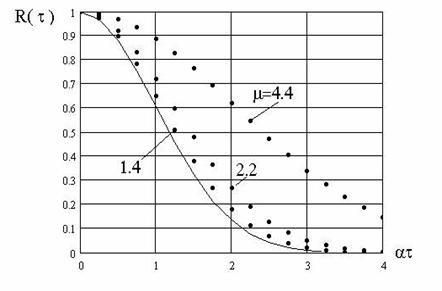
Рис. 2. Экспериментальный вид нормированной корреляционной функции профильтрованного шума.
В [6] приводится один
приближенный подход к расчету
![]() , точность которого предположительно
возрастает при
, точность которого предположительно
возрастает при
![]() .
Однако, сравнение с результатами моделирования показало его применимость только
для узкого диапазона значений параметра
.
Однако, сравнение с результатами моделирования показало его применимость только
для узкого диапазона значений параметра
![]() , внутри которого отклонение точных и расчетных
значений
, внутри которого отклонение точных и расчетных
значений
![]() меньше
меньше
![]() . На
рис. 2 приведены экспериментальные
значения нормированной корреляционной функции
. На
рис. 2 приведены экспериментальные
значения нормированной корреляционной функции
![]() при различных значениях параметра
при различных значениях параметра
![]() . Здесь же пунктиром
показана корреляционная функция
. Здесь же пунктиром
показана корреляционная функция
![]() . Для процессов с корреляционной функцией
. Для процессов с корреляционной функцией
![]() зависимости
аналогичны.
зависимости
аналогичны.
3. Характеристики обнаружения
Итак, после этапа
медианной фильтрации на интервале
![]() имеется процесс
имеется процесс
где
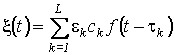 ;
;
![]() с вероятностью
с вероятностью
![]() , и
, и
![]() с вероятностью
с вероятностью
![]() . Вероятность
. Вероятность
![]() вычисляется в соответствии с
формулами (5),(6) и (8), а бегущий индекс
вычисляется в соответствии с
формулами (5),(6) и (8), а бегущий индекс
![]() отражает процесс скользящей медианной
фильтрации. Процесс
отражает процесс скользящей медианной
фильтрации. Процесс
![]() поступает
на приемник, рассчитанный на обработку полезного сигнала
поступает
на приемник, рассчитанный на обработку полезного сигнала
![]() на фоне флуктуационного шума
на фоне флуктуационного шума
![]() . На выходе приемника формируется
статистика
. На выходе приемника формируется
статистика
В выражении (10)
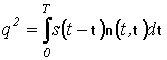 - отношение сигнал/шум;
- отношение сигнал/шум;
![]() - решение интегрального
уравнения
- решение интегрального
уравнения
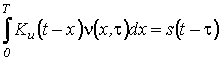 .
Параметр
.
Параметр
![]() имеет
смысл отношения сигнал/помеха для
имеет
смысл отношения сигнал/помеха для
![]() - го импульса потока на выходе линейной
части приемника
- го импульса потока на выходе линейной
части приемника
Нормированные сигнальные функции
представляют отклик приемника на сигнальный и
помеховый импульсы. Они полагаются непрерывными, а
![]() - дважды дифференцируемой
функцией. Причем,
- дважды дифференцируемой
функцией. Причем,
![]() ,
,
![]() .
.
Асимптотически оптимальным правилом обнаружения сигнала с неизвестными параметрами является алгоритм принятия решения по методу максимального правдоподобия
Порог обнаружения
![]() выбирается в
соответствии с выбранным критерием. Расчет вероятностей ложной тревоги
выбирается в
соответствии с выбранным критерием. Расчет вероятностей ложной тревоги
![]() и пропуска сигнала
и пропуска сигнала
![]() может быть выполнен по методике, разработанной в [7].
может быть выполнен по методике, разработанной в [7].
Величина абсолютного
максимума
![]() ,
,
![]() может быть обусловлена либо полезным сигналом, либо
может быть обусловлена либо полезным сигналом, либо
![]() - м импульсом помехи,
либо шумовым выбросом
- м импульсом помехи,
либо шумовым выбросом
![]() .
Функция распределения абсолютного максимума гауссовского процесса
.
Функция распределения абсолютного максимума гауссовского процесса
![]() на интервале
на интервале
![]() определяется выражением
определяется выражением
Здесь параметр
![]() имеет смысл числа элементов разрешения по
временному положению полезного сигнала на интервале
имеет смысл числа элементов разрешения по
временному положению полезного сигнала на интервале
![]() . Формула (14) асимптотически
точна при
. Формула (14) асимптотически
точна при
![]() и
и
![]() . Обобщая методику
расчета
. Обобщая методику
расчета
![]() и
и
![]() из работы [7], можно записать
из работы [7], можно записать
где
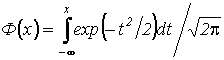 , а
, а
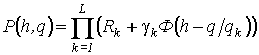 .
.
Учитывая, что
![]() , а
, а
![]() можно переписать
можно переписать
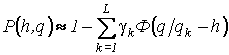 .
.
В частном случае одинаковых амплитуд импульсов в
потоке
![]() ,
,
![]() . Тогда
. Тогда
![]() . Если этап медианной
фильтрации отсутствует, то вероятности ошибок
. Если этап медианной
фильтрации отсутствует, то вероятности ошибок
![]() и
и
![]() имеют вид аналогичный (15). Только в
этом случае
имеют вид аналогичный (15). Только в
этом случае
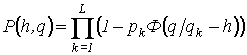 ,
где
,
где
![]() -
вероятность присутствия
-
вероятность присутствия
![]() - го импульса в потоке Бернулли. Как уже
упоминалось,
- го импульса в потоке Бернулли. Как уже
упоминалось,
![]() .
.
Рис. 3. Результаты расчета вероятности пропуска сигнала.
На рис. 3 приведены
результаты расчетов вероятности пропуска
![]() при выборе порога
при выборе порога
![]() по критерию Неймана – Пирсона
при значении
по критерию Неймана – Пирсона
при значении
![]() .
Расчет выполнялся для следующих значений параметров:
.
Расчет выполнялся для следующих значений параметров:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() . Ширина апертуры
. Ширина апертуры
![]() соответствует случаю отсутствия
медианной фильтрации. Пунктиром показан случай отсутствия импульсной ппомехи.
соответствует случаю отсутствия
медианной фильтрации. Пунктиром показан случай отсутствия импульсной ппомехи.
Полученные формулы
являются асимптотически точными при
![]() ,
,
![]() и приближенными при конечных значениях
указанных параметров. Методом статистического моделирования для частного случая
одного и двух мешающих сигналов установлено [7], что совпадение расчетных и экспериментальных значений наблюдается при
и приближенными при конечных значениях
указанных параметров. Методом статистического моделирования для частного случая
одного и двух мешающих сигналов установлено [7], что совпадение расчетных и экспериментальных значений наблюдается при
![]() ,
,
![]() и порогах
и порогах
![]() , вероятность превышения которых
меньше
, вероятность превышения которых
меньше
![]() .
Результаты моделирования показали, что при значениях
.
Результаты моделирования показали, что при значениях
![]() влиянием остаточной помехи можно
пренебречь. Ее учет необходим при
влиянием остаточной помехи можно
пренебречь. Ее учет необходим при
![]() , когда амплитуды мешающих сигналов на
выходе приемника после двухэтапной обработки соизмерима с амплитудой полезного
сигнала.
, когда амплитуды мешающих сигналов на
выходе приемника после двухэтапной обработки соизмерима с амплитудой полезного
сигнала.
В заключении отметим, что
медианная фильтрация на первом этапе целесообразна, только при
![]() , где
, где
![]() - вероятность
прохождения импульса помехи через фильтр. Для интенсивных потоков медианная
фильтрация становится неэффективной. Метод медианной фильтрации может стать
полезным дополнением к процедуре помехоустойчивого кодирования - декодирования,
особенно в случае интенсивных помех, приводящих к появлению кратных ошибок.
- вероятность
прохождения импульса помехи через фильтр. Для интенсивных потоков медианная
фильтрация становится неэффективной. Метод медианной фильтрации может стать
полезным дополнением к процедуре помехоустойчивого кодирования - декодирования,
особенно в случае интенсивных помех, приводящих к появлению кратных ошибок.
Литература
1. Ратынский М.В. Основы сотовой связи. /Под ред. Д.Е. Зимина- М.: Радио и связь, 1998, -248 с.
2. Финк Л.М. Теория передачи дискретных сообщений, М.: Сов. Радио, 1970,- 728с.
3. Обнаружение радиосигналов /П.С. Акимов, Ф.Ф. Евстратов, С.И. Захаров и др.; Под ред. А.А. Колосова,-М.: Радио и связь, 1989,- 288 с.
4. Большаков И.А., Ракошиц В.С. Прикладная теория случайных потоков, М.: Сов. радио, 1978,- 248с.
5. Радченко Ю.С., Радченко Т.А., Назарьев А.Л. Вероятностные характеристики случайных процессов на выходе медианного фильтра.// Тезисы докладов 51 научной сессии РНТО РЭС им. А.С. Попова, посвященной Дню радио, Москва, 1996, часть II,- 169с.
6. Быстрые алгоритмы в цифровой обработке изображений. Преобразования и медианные фильтры / Под ред. Хуанга, Пер. с англ.- М.: Радио и связь, 1984,- 224с.
7. Куликов, Ю.С. Радченко, А. П. Трифонов Характеристики приемника максимального правдоподобия при наличии квазидетерминированной помехи, Изв. ВУЗов, Радиоэлектроника, N9,1978, С.4 – 9.
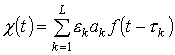
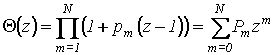
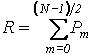 . (
. ( 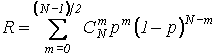 . (
. ( 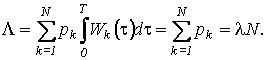 ( 7 )
( 7 )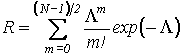 . (
. ( 
 . (
. (  (
(  ;
;
 (
( 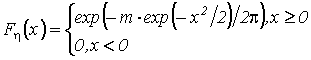 (
(