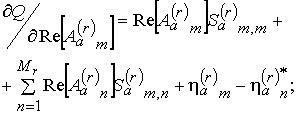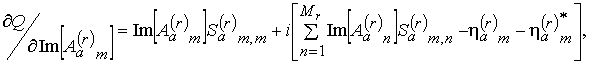|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 7, 2003 |
|
МЕТОД ФАЗОВОГО СИНТЕЗА ЛИНЕЙНОЙ АНТЕННОЙ РЕШЕТКИ С НЕИДЕНТИЧНЫМИ ИЗЛУЧАТЕЛЯМИ ПО ЗАДАННОЙ ВЕКТОРНОЙ ДИАГРАММЕ НАПРАВЛЕННОСТИ
Мищенко С.Е., Тупичкин Д.В.; e-mail: mihome@jeo.ru
Ростовский военный институт ракетных войск
Получена 10 июля 2003 г.
Предложен метод фазового синтеза антенной решетки скрещенных электрических вибраторов по заданной векторной диаграмме направленности. Каждый излучатель в составе решетки повернут относительно соседнего на угол 45 градусов. Каждый электрический вибратор в составе излучателя управляется независимо. После выполнения преобразования Фурье диаграмм направленности излучателей задача векторного синтеза сводится к решению трех систем линейных уравнений. Каждая из систем уравнений решена методом проектируемого градиента. Приведены результаты численных исследований.
В работе [1] была рассмотрена задача векторного синтеза антенной решетки (АР) скрещенных электрических вибраторов по заданной векторной диаграмме направленности (ДН). Реализация подхода, предложенного в [1], основана на разделении задачи векторного синтеза на две задачи синтеза АР с линейной поляризацией сигнала. Данное разделение возможно при условии, что скрещенные электрические вибраторы в составе антенны ориентированы вдоль осей выбранной декартовой системы координат. Кроме того, каждый электрический вибратор должен управляться независимо с отдельного входа. В то же время в ряде практических случаев вызывает интерес построение АР скрещенных вибраторов, в которой излучатели повернуты относительно соседних в плоскости раскрыва на угол 45 градусов. Такая конфигурация АР позволяет, в частности, с большей плотностью размещать излучатели. При этом возникает необходимость решения задачи векторного синтеза АР с неидентичными излучателями.
Цель данной работы состоит в разработке метода фазового синтеза линейной АР с неидентичными излучателями по заданной векторной ДН. Каждый излучатель синтезируемой АР имеет два независимо управляемых входа.
Пусть в состав АР входят излучатели, состоящие из горизонтальных скрещенных симметричных электрических вибраторов с совмещенными центрами. Будем считать, что каждый электрический вибратор в составе излучателя может управляться независимо. При этом каждый следующий излучатель в составе решетки повернут относительно предыдущего на угол 45 градусов в плоскости излучающего раскрыва. Подобная конфигурация антенны позволяет разбить АР на две подрешетки, в каждой из которых ориентация излучателей идентична.
Векторная ДН рассматриваемой АР может быть представлена в виде суперпозии двух проекций на орты сферической системы координат
где
![]() ;
; ![]() ;
; ![]() ,
, ![]() и
и ![]() ,
, ![]() - комплексные амплитуды возбуждения
- комплексные амплитуды возбуждения ![]() -ых электрических вибраторов в
составе первой и второй подрешеток соответственно;
-ых электрических вибраторов в
составе первой и второй подрешеток соответственно; ![]() и
и ![]() - координаты размещения излучателей в составе первой и второй
подрешеток;
- координаты размещения излучателей в составе первой и второй
подрешеток; ![]() и
и
![]() - количество излучателей в составе
первой и второй подрешеток соответственно;
- количество излучателей в составе
первой и второй подрешеток соответственно; ![]() - волновое число. Геометрия задачи приведена на
рис. 1.
- волновое число. Геометрия задачи приведена на
рис. 1.
Анализ выражений (2) и
(3) позволяет сделать вывод о том, что подход к решению задачи синтеза,
предложенный в работе
[1], к
задаче синтеза рассматриваемой АР использован быть не может. Однако в частном случае, когда АР является линейной, а шаг
между излучателями близок или равен ![]() декомпозиция задачи векторного синтеза на
ряд более простых задач все-таки возможна.
декомпозиция задачи векторного синтеза на
ряд более простых задач все-таки возможна.
Пусть линейная АР ориентирована вдоль оси 0X
декартовой системы координат (см. рис. 1). В этом случае выражения (2) и (3)
могут быть значительно упрощены. Следует отметить, что для подрешетки,
излучатели которой повернуты на 45 градусов, на основании выражения (4)
выполняется равенство
![]() . Поэтому для любого направления сканирования
единичный коэффициент эллиптичности будет иметь место в том случае, когда
. Поэтому для любого направления сканирования
единичный коэффициент эллиптичности будет иметь место в том случае, когда
![]() . Выполнение этого условия позволяет представить выражения (2) и (3)
для линейной АР в виде:
. Выполнение этого условия позволяет представить выражения (2) и (3)
для линейной АР в виде:
Из выражений (7) и (8) следует, что ДН рассматриваемой линейной АР зависит от трех амплитудно-фазовых распределений.
Рассмотрим теперь решение задачи синтеза линейной АР
с шагом между излучателями
![]() в
следующей постановке. Пусть известны функции, описывающие ДН излучателей АР, определяемые
выражениями (4)-(6). Заданы комплексные функции
в
следующей постановке. Пусть известны функции, описывающие ДН излучателей АР, определяемые
выражениями (4)-(6). Заданы комплексные функции
![]() и
и
![]() , определяющие компоненты желаемой векторной ДН
рассматриваемой антенны (
, определяющие компоненты желаемой векторной ДН
рассматриваемой антенны (![]() ). Требуется найти комплексные амплитуды
). Требуется найти комплексные амплитуды
![]() ,
,
![]() и
и
![]() ,
обеспечивающие величину среднеквадратического уклонения компонент
синтезированной ДН от заданной, не превышающей заданной величины.
,
обеспечивающие величину среднеквадратического уклонения компонент
синтезированной ДН от заданной, не превышающей заданной величины.
Для осуществления декомпозиции задачи векторного синтеза АР с неидентичными излучателями на две задачи синтеза АР с идентичными излучателями выполним Фурье преобразование функций, описывающих ДН излучателей АР для каждой подрешетки в отдельности.
где ![]() - волновое число;
- волновое число; ![]() ;
; ![]() - номер подрешетки (в зависимости от номера подрешетки индекс
- номер подрешетки (в зависимости от номера подрешетки индекс ![]() изменяется от единицы
до
изменяется от единицы
до ![]() или
или ![]() ).
).
Для вычисления
коэффициентов Фурье воспользуемся правилом интегрирования по частям, обозначив ![]() ;
; ![]()
![]() .
.
С учетом данных обозначений выражение (9) примет вид
После вычисления первого слагаемого получим
При вычислении второго
слагаемого учтем, что функции ![]() принадлежат к классу целых функций
конечной степени. Это означает, что для описания функции
принадлежат к классу целых функций
конечной степени. Это означает, что для описания функции ![]() могут использоваться степенные
полиномы вида
могут использоваться степенные
полиномы вида
где ![]() – постоянные коэффициенты.
– постоянные коэффициенты.
При этом результат
вычисления второго слагаемого в (9) будет зависеть от степени полинома. Так,
для полинома нулевой степени второе слагаемое равно нулю, коэффициенты ![]() определяются выражением
(11).
определяются выражением
(11).
В случае, когда функции ![]() описываются полиномами
более высоких степеней, для вычисления второго слагаемого в выражении (10)
также приходится использовать интегрирование по частям. При этом результирующее
выражение будет содержать слагаемые вида:
описываются полиномами
более высоких степеней, для вычисления второго слагаемого в выражении (10)
также приходится использовать интегрирование по частям. При этом результирующее
выражение будет содержать слагаемые вида:
После подстановки пределов получим выражение, позволяющее вычислить коэффициенты разложения в ряд Фурье ДН излучателей.
Однако для анализа
номеров ненулевых гармоник Фурье в спектре излучателей, ДН которых описываются
четными функциями, окончательные выражения не обязательны. Действительно, если функции ![]() являются четными, то описывающий их
степенной полином будет состоять из слагаемых с четными степенями параметра
u. При этом в знаменателе выражения
(13) показатель j+1 есть число
нечетное. Это означает, что номера ненулевых гармоник Фурье в разложениях
излучателей с четными амплитудными ДН будут совпадать с номерами ненулевых
гармоник Фурье в разложениях изотропных излучателей. То есть для определения
ненулевых гармоник Фурье в спектрах излучателей достаточно воспользоваться
выражением (11) положив
являются четными, то описывающий их
степенной полином будет состоять из слагаемых с четными степенями параметра
u. При этом в знаменателе выражения
(13) показатель j+1 есть число
нечетное. Это означает, что номера ненулевых гармоник Фурье в разложениях
излучателей с четными амплитудными ДН будут совпадать с номерами ненулевых
гармоник Фурье в разложениях изотропных излучателей. То есть для определения
ненулевых гармоник Фурье в спектрах излучателей достаточно воспользоваться
выражением (11) положив ![]() .
.
Из анализа выражения (11) следует, что при
![]() спектр
спектр
![]() -го излучателя будет содержать лишь одну ненулевую
гармонику Фурье, номер которой связан с номером излучателя в составе АР.
-го излучателя будет содержать лишь одну ненулевую
гармонику Фурье, номер которой связан с номером излучателя в составе АР.
Последний вывод применительно к рассматриваемой задаче позволяет утверждать, что излучатели первой и второй подрешеток управляют ортогональными наборами гармоник Фурье. Оба эти набора могут присутствовать в спектре заданной ДН. Поэтому для разделения сформулированной задачи синтеза необходимо найти набор гармоник Фурье, образующих спектр заданной ДН и выделить в нем наборы гармоник, которыми управляют первая и вторая подрешетки соответственно.
Пусть
![]() и
и
![]() ,
,
![]() и
и
![]() - ортогональные наборы гармоник Фурье, образующие спектры компонент
- ортогональные наборы гармоник Фурье, образующие спектры компонент
![]() и
и
![]() заданной векторной ДН для первой и второй
подрешеток соответственно. При определении заданной будем полагать, что
заданной векторной ДН для первой и второй
подрешеток соответственно. При определении заданной будем полагать, что
![]() .
.
Из ненулевых наборов гармоник Фурье спектров ДН
излучателей составим матрицы
![]() ,
,
![]() и
и
![]() . Будем считать, что количество строк в матрицах и
размерности векторов
. Будем считать, что количество строк в матрицах и
размерности векторов
![]() и
и
![]() ,
,
![]() и
и
![]() ,
,
![]() и
и
![]() совпадают. Это требование обусловлено тем, что набор ненулевых
гармоник Фурье в спектрах ДН излучателей ограничен, следовательно, и реализуемая
ДН в своем спектре Фурье должна содержать конечный набор ненулевых гармоник.
совпадают. Это требование обусловлено тем, что набор ненулевых
гармоник Фурье в спектрах ДН излучателей ограничен, следовательно, и реализуемая
ДН в своем спектре Фурье должна содержать конечный набор ненулевых гармоник.
С учетом введенных обозначений и сделанных допущений решение задачи векторного синтеза может быть сведено к независимому решению трех систем линейных уравнений вида:
Следует отметить, что в отличие от метода [2], где система уравнений для задачи синтеза могла быть переопределенной, а количество уравнений в системе соответствовало числу ненулевых гармоник, в рассматриваемом случае каждая из систем уравнений (14)-(16) будет содержать количество уравнений, соответствующее числу элементов в составе подрешетки. Это означает, что при выборе заданной ДН необходимо следить за тем, чтобы количество ненулевых младших гармоник Фурье в ее спектре не превышало числа излучателей.
Решение систем уравнений (14)-(16) может быть осуществлено любым из известных методов. С практической точки зрения представляет интерес решение задачи фазового синтеза, которое может быть получено методом проектируемого градиента [3]. При этом градиент целевой функции будет определяться выражениями вида:
где
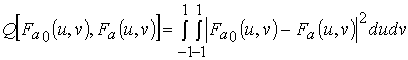
- целевая функция; символ “*” обозначает операцию комплексного сопряжения;
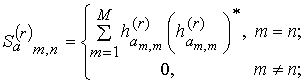
![]() ;
;
![]() ;
;
![]() .
.
В качестве примера решения задачи векторного синтеза рассмотрим решение 33-х элементной линейной АР скрещенных симметричных электрических вибраторов с длиной плеча 0.25l, поочередно развернутых друг относительно друга на угол 45 градусов. Будем считать, что излучатели размещены с постоянным шагом - 0,5l. Крайние излучатели АР ориентированы таким образом, что их электрические вибраторы ориентированы вдоль осей декартовой системы координат.
При решении задачи синтеза в качестве заданной ДН выберем функцию, получаемую при синфазном возбуждении 33-х элементной ФАР изотропных излучателей, возбужденных спадающим по закону косинус распределению. В качестве заданного амплитудного распределения выберем также косинусное возбуждение, но с подставкой 0,5 (максимальная амплитуда центрального излучателя равна единице). Начальное фазовое распределение было сформировано с использованием метода быстроколеблющейся фазы [3].
Для решения каждой из сформированных систем уравнений потребовалось от пяти до десяти итераций.
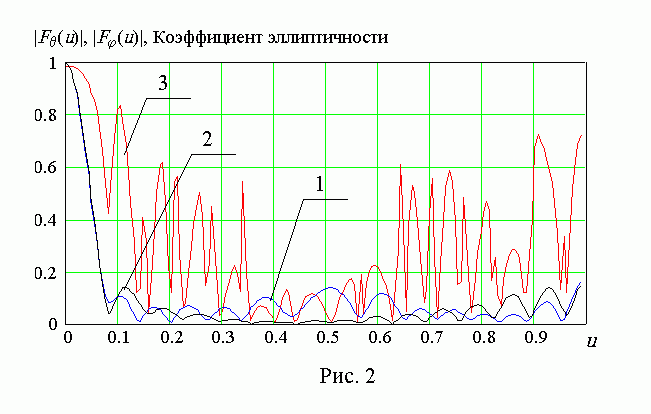
На рис. 2 приведены
![]() - и
- и
![]() -компоненты синтезированной векторной ДН, соответствующие
кривые обозначены номерами 1 и 2. Кривая 3 иллюстрирует зависимость коэффициента
эллиптичности АР. Как видно из рис.2, наиболее высокие значения коэффициента
эллиптичности получены в пределах главного луча ДН. Для остальных направлений
значения коэффициента эллиптичности ниже 0,8. Полученная зависимость отражает
возможности АР с неидентичными излучателями при управлении поляризационными
характеристиками. Следует отметить, что коэффициент эллиптичности синтезированной
АР в области боковых лепестков в значительной степени определяется выбором
начального фазового распределения.
-компоненты синтезированной векторной ДН, соответствующие
кривые обозначены номерами 1 и 2. Кривая 3 иллюстрирует зависимость коэффициента
эллиптичности АР. Как видно из рис.2, наиболее высокие значения коэффициента
эллиптичности получены в пределах главного луча ДН. Для остальных направлений
значения коэффициента эллиптичности ниже 0,8. Полученная зависимость отражает
возможности АР с неидентичными излучателями при управлении поляризационными
характеристиками. Следует отметить, что коэффициент эллиптичности синтезированной
АР в области боковых лепестков в значительной степени определяется выбором
начального фазового распределения.
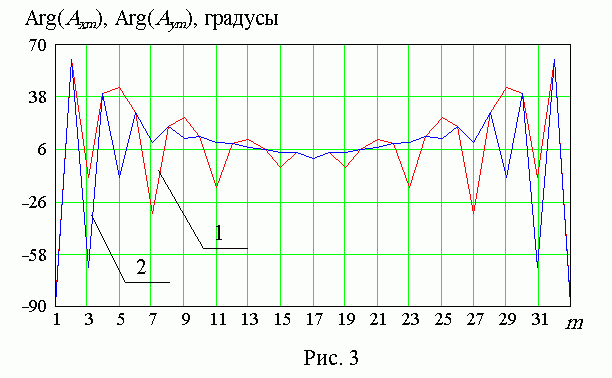
На рис. 3 приведены фазовые распределения, найденные в результате решения задачи синтеза. Значения фаз возбуждения излучателей кривой 1 соответствуют возбуждению электрических вибраторов, ориентированных вдоль оси 0Х для первой подрешетки и коллинеарных электрических вибраторов второй подрешетки. Кривая 2 описывает фазовое распределение в вибраторах, ориентированных вдоль оси 0Y первой подрешетки и коллинеарных электрических вибраторов второй подрешетки. Интересно, что электрические вибраторы второй подрешетки являются синфазными. Сдвиг фаз, равный 90 градусов, между излучателями данной подрешетки приводит к значительному росту боковых лепестков.
Таким образом, в работе предложен метод фазового
синтеза, позволяющий формировать ДН линейной АР с неидентичными излучателями.
Предложенный метод позволяет свести задачу векторного фазового синтеза АР из
двух подрешеток с идентичными излучателями к решению трех независимых систем
линейных уравнений. В основе предложенного метода лежит условие ортогональности
спектров Фурье ДН излучателей решетки с шагом
![]() . При увеличении количества подрешеток с идентичными излучателями будет
увеличиваться количество систем уравнений. Поскольку решение каждой из систем
уравнений является приближенным, то в случае большого числа подрешеток следует
ожидать увеличения расхождения между заданной и синтезируемой ДН. Работа
выполнена при финансовой поддержке РФФИ (коды проекта № 01-01-00030 и №
03-01-06411).
. При увеличении количества подрешеток с идентичными излучателями будет
увеличиваться количество систем уравнений. Поскольку решение каждой из систем
уравнений является приближенным, то в случае большого числа подрешеток следует
ожидать увеличения расхождения между заданной и синтезируемой ДН. Работа
выполнена при финансовой поддержке РФФИ (коды проекта № 01-01-00030 и №
03-01-06411).
ЛИТЕРАТУРA
1. Мищенко С.Е., Тупичкин Д.В. Фазовый синтез векторной диаграммы направленности плской антенной решетки по методу проектируемого градиента // Сб. докладов IV международного симпозиума по электромагнитной совместимости и электромагнитной экологии "ЭМС-2001", 19-22.06.01г. Ст.-Петербург, с.417-420.
2. Габриэльян Д.Д., Мищенко С.Е. Метод амплитудно-фазового синтеза антенной решетки произвольной геометрии // Радиотехника и электроника, 1995, Т.40, № 7, С.1038-1041.
3. Зелкин Е.Г., Соколов В.Г. Методы синтеза антенн: Фазированные антенные решетки и антенны с непрерывным раскрывом. - М.: Сов. Радио, 1980, 296с.
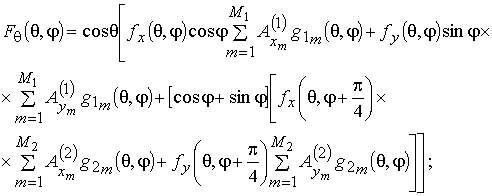
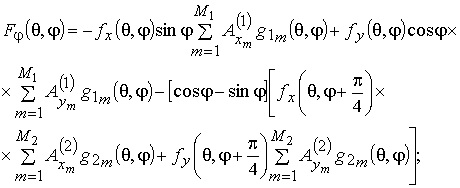

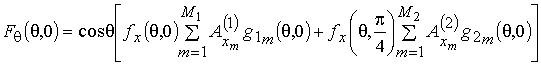 ;(7)
;(7)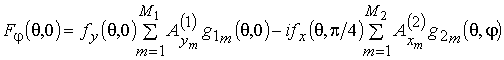 . (8)
. (8)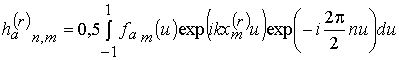 , (9)
, (9)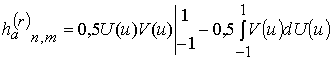 . (10)
. (10)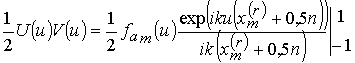 . (11)
. (11)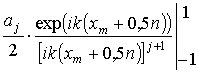 . (13)
. (13)