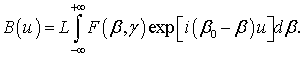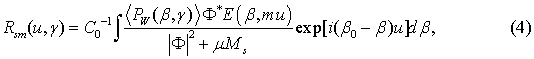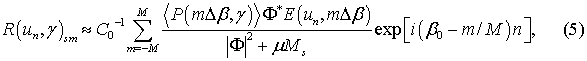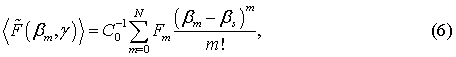| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" №7, 2007 |
УДК 519.6: 535.36: 620.18:
621.373: 681.4
КОГЕРЕНТНАЯ ВОЛНОВОДНАЯ ОПТИЧЕСКАЯ МИКРОСКОПИЯ СТАТИСТИЧЕСКИХ МИКРООБЪЕКТОВ
Получена 20 июня 2007 г.
Описан метод когерентной волноводной оптической микроскопии, основанный на явлении волноводного рассеяния света. Возможности метода продемонстрированы на компьютерной модели. Показано, что разработанный автором алгоритм позволяет определить радиусы корреляции эффективной неровности поверхности размером λ/60–15λ с ошибкой не более 5–25%, а соответствующую среднеквадратичную высоту 25–150 Å с ошибкой менее 5–35%. Показано, что метод волноводного рассеяния позволяет получить статистическую информацию за одно измерение с достаточно большой площади поверхности (объема) с существенным превышением дифракционного предела, т.е. позволяет перейти в нанометровый диапазон.
1. ВВЕДЕНИЕ
В последние годы возник устойчивый интерес к разработке высокоточных оптических методов неразрушающего контроля и идентификации нано- и микрообъектов в биологии, медицине, экологии, биофизике, биохимии, микробиологии, микро- и наноэлектронике, лазерной и интегральной оптике и других наукоемких областях исследования [1-20]. Это связано в первую очередь с высокой чувствительностью оптических методов, а также с возможностью оперативного неинвазивного исследования микрообъектов как биологического, так и не биологического происхождения. Хорошо известны следующие методы исследования, позволяющие достичь высокого разрешения: электронная вакуумная микроскопия, сканирующая туннельная вакуумная микроскопия, атомно-силовая микроскопия, конфокальная лазерная микроскопия, оптическая гетеродинная профилометрия и микроскопия, ближнепольная оптическая микроскопия и ряд других (см., например, список литературы к работам [1-20]). В настоящей работе рассмотрен относительно новый лазерный метод исследования и контроля – метод волноводной оптической микроскопии (ВОМ).
Оптические методы позволяют по тем или иным характеристикам и параметрам, например, рассеянного излучения восстановить характеристики и определить параметры исследуемого объекта. Это могут быть характеристики и параметры, как поверхности объекта, так и его внутренней структуры. Под элементами внутренней структуры или поверхности объекта можно понимать некоторые функциональные элементы [3], геометрические параметры которых могут быть измерены данным методом. Например, в качестве функциональных элементов можно рассматривать клетки ткани, белковые молекулы, микрочастицы компонентов различных материалов или поры в них, микрообъекты (функциональные элементы с минимальной связью между ними, например, во взвесях) и др. От совокупности данных элементов зависят физические параметры объекта [3, 21, 22]. У биологических объектов функциональные элементы определяют еще и динамические свойства тканей, например, рост и функционирование. В связи с этим решение задачи восстановления характеристик и определения геометрических размеров ансамблей функциональных элементов с превышением разрешения Аббе-Рэлея является, несомненно, актуальной задачей как для дисциплин биологического (биофизика, генетика и др.), так и технического профиля (наноэлектроника, интегральная оптика и др.). Следует отметить, что проблема преодоления классического дифракционного предела разрешения Аббе-Рэлея (δA-R = λ(2NA)-1, где λ – длина волны лазерного излучения, NA – числовая апертура микроскопа) является одной из фундаментальных проблем оптики и в частности оптической микроскопии [1-6, 11-14, 20]. Она имеет уже довольно продолжительную историю – более 120 лет, начиная с первых публикаций Аббе по проблемам формирования изображения в 1873 году.
На языке оптической микроскопии характеристики поверхности обычно сводятся к функции профиля поверхности или автокорреляционной функции, в зависимости от характера неровности поверхности. Например, неровность профиля поверхности может быть связана с ее естественной шероховатостью, волнистостью, а может быть обусловлена наличием на достаточно гладкой поверхности подложки ансамбля некоторых биологических микрообъектов (некоторая эффективная неровность) и т.д. При исследовании ансамбля микрообъектов с близкими параметрами (далее – объект) часто продуктивным оказывается статистический подход, при котором определяются характеристики и параметры, характеризующие свойства ансамбля в целом. В этом случае удается описать и свойства одиночного микрообъекта из ансамбля, хотя и в усредненном виде. Такой подход позволяет получить ряд новых сведений об исследуемых микрообъектах, недоступных при анализе другими методами. Естественно, эти данные не могут полностью заменить результаты наблюдения с помощью классического оптического микроскопа, – их следует рассматривать как необходимое дополнение к последним. Одним из методов, позволяющих реализовать статистический подход, является метод ВОМ [5-14].
Метод (когерентной) волноводной оптической микроскопии основан на использовании явления волноводного "освещения" исследуемого объекта, находящегося в волноводном слое, лазерным излучением направляемой волноводной моды. Под освещением здесь понимается рассеяние когерентного излучения заданной моды на исследуемом объекте и формирование диаграммы рассеяния, несущей информацию об основных характеристиках и параметрах объекта. Т.е. в качестве оптического зонда объекта выступает характерная направляемая мода, поддерживаемая структурой волновода. Управляя свойствами данного "зонда" можно управлять контрастными и другими характеристиками рассеянного излучения, формирующего оптический образ объекта что, несомненно, важно при исследовании малоконтрастных объектов [5-9, 12, 14].
Волноводный оптический микроскоп может быть выполнен как самостоятельное устройство, так и как комбинация интегрально-оптического, например, планарного оптического волновода (ПВ) и классического оптического микроскопа. Рассеянное лазерное излучение (наблюдаемых мод), формирующее оптический образ объекта, обычно регистрируется фотодетектором в ближней или дальней зоне (или в эквивалентной ей Фурье-плоскости) волноводного оптического микроскопа в виде излучательных воздушных мод и излучательных мод подложки ПВ. Если условия рассеяния волноводной моды на статистическом ансамбле микрообъектов удовлетворяют первому приближению теории возмущений, то регистрируемая точечным (функция фильтрации является дельта функцией) фотодетектором в дальней зоне функция отклика (диаграмма рассеяния) микроскопа является фактически отображением функции спектральной плотности (ФСП) ансамбля в пространстве волновых чисел. Как известно, в этом случае рассеяние зависит только от статистических характеристик второго порядка ансамбля микрообъектов: ФСП или ее Фурье-преобразования – автокорреляционной функции (АКФ). АКФ и ФСП содержат всю информацию об основных параметрах исследуемого объекта [6, 7, 14-16, 19].
2. ХАРАКТЕРИСТИКИ И ПАРАМЕТРЫ ВОЛНОВОДНОГО МИКРОСКОПА
Основными характеристиками волноводного оптического микроскопа (рис. 1) являются: волноводный оптический фактор (или оптическая передаточная функция (ОПФ)) и функция рассеяния точки (ФРТ), являющаяся фурье-преобразованием ОПФ [6-9]. Основными параметрами волноводного оптического микроскопа являются: числовая апертура и параметры ПВ – показатели преломления обрамляющей среды, тонкого волноводного слоя и подложки n1, n2 и n3 соответственно, толщина волновода h, а также эффективный показатель преломления γ. Последний параметр оказывает основное влияние на вид ОПФ, а следовательно и на ход решения прямой и обратной задач. ПВ может содержать как одиночный микрообъект, так и ансамбль микрообъектов, например, статистическую неровность поверхности подложки ПВ или ансамбль объемных неоднородностей волноводного слоя (далее – исследуемый объект).
Компьютерное моделирование проводилось для практически реализуемого волноводного оптического микроскопа, основанного на простом симметричном ПВ с n1 = n3 = 1.46 (кварцевое стекло) и n2 = 1.59 (оптически прозрачная жидкость) для λ = 0.63 мкм (гелий-неоновый лазер). Близкую разность показателей имеет, например, структура эпидермис–кровь (Δn12 = 1.50–1.35 = 0.15). Заметим, что выбор вещества для волноводного слоя принципиален в случае исследования биологических микрообъектов. Полагается, что исследуемые эффективные неровности однотипны и принадлежат одному эргодическому ансамблю, поэтому определяемые статистические характеристики (АКФ и ФСП) и параметры неровности поверхности (среднеквадратичная высота и радиус (интервал) корреляции) одинаковы для неровностей обеих границ волновода. Поэтому далее будем говорить только об одной поверхности.
Рис. 1. Схема волноводного оптического микроскопа: 1–3 – планарный оптический волновод; 1, 3 – кварцевые пластинки; 2 – жидкостный волноводный слой; 4 – иммерсия; 5 – кварцевая полусфера; Л – линза; ФД – фотодетектор; АЦП – аналого-цифровой преобразователь. На вставке вверху слева: статистический ансамбль модельных биологических микрообъектов, расположенных на поверхностях пластинок внутри волноводного слоя.
Детальный анализ динамики ОПФ и ФРТ волноводного оптического микроскопа позволяет найти оптимальные характеристики волноводного оптического микроскопа и определить соответствующее оптимальное значение γ [8]. Оптимизация характеристик и параметров микроскопа сводится к синтезу ОПФ максимально близкой в среднеквадратичном смысле к некоторой идеальной функции, обеспечивающей прохождение сигнала через оптическую систему с минимальными искажениями.
3. ПРЯМАЯ ЗАДАЧА ВОЛНОВОДНОЙ ОПТИЧЕСКОЙ МИКРОСКОПИИ
Достижение сверхразрешения в волноводной оптической микроскопии тесно связано с корректным решением прямой и обратной задач теории волноводного рассеяния света [5-19]. Решение прямой задачи заключается в нахождении функции отклика (диаграммы рассеяния лазерного излучения) волноводного оптического микроскопа на исследуемый объект, главным образом в ближней зоне, дальней зоне (или в эквивалентной ей Фурье-плоскости) или плоскости изображения. Если интенсивность отклика измеряется в дальней зоне с помощью точечного фотоприемника, то зашумленная функция отклика микроскопа P(β, γ) может быть представлена в виде [6, 7, 14-19]:
где β – продольная составляющая постоянной распространения мод излучения, формирующих оптический образ объекта; C0 – нормировочная постоянная; Φ(β, γ) – волноводный оптический фактор (или оптическая передаточная функция системы); F(β, γ) – ФСП статистического ансамбля микрообъектов; W(β, γ) – интенсивность «белого» аддитивного действительного шума, заданного в области измерения диаграммы рассеяния; <…> – усреднение по эргодическому ансамблю статистически идентичных систем [23]. Модельная ФСП эффективной статистической стационарной неровности обычно берется в виде гауссовой функции:
В формуле (2) L – длина нерегулярного участка ПВ (области, содержащей статистический ансамбль исследуемых микрообъектов), β0 = kγ – постоянная распространения направляемой волноводной моды; k = 2π/λ. Для объемных неоднородностей гауссова ФСП имеет аналогичное (2) выражение с той разницей, что вместо среднеквадратичной высоты эффективных неровностей σ стоит среднеквадратичное отклонение показателя преломления волноводного слоя от среднего значения
, а вместо радиуса корреляции поверхностных неровностей r – радиус корреляции неоднородностей показателя преломления
(характерных объемных неоднородностей). Использование нормального распределения (2) при модельном анализе закономерно, т.к. в силу центральной предельной теоремы большинство реальных случайных процессов в физике, биологии и т.д. является гауссовым [23].
По теореме Винера-Хинчина автокорреляционная функция B(u) является Фурье-преобразованием от функции спектральной плотности F(β, γ):
Выполнив интегрирование, получаем аналитическое выражение для АКФ:
где r – радиус корреляции (характерный латеральный размер эффективных неровностей профиля поверхности, обусловленных наличием исследуемых биологических микрообъектов на ровной поверхности подложки ПВ); u = z – z', z и z' – координаты в плоскости объекта. Напомним, что для случайных эргодических процессов АКФ является мерой статистического (структурного) подобия функций B(z) и B(z') усредненной по ансамблю.
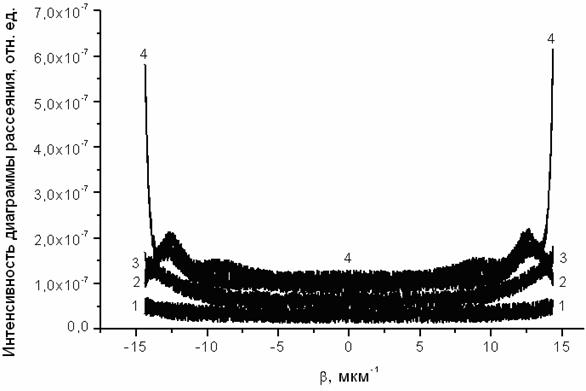
На рис. 2 показаны нормированные двумерные (в плоскости падения XZ) диаграммы рассеяния волноводного оптического микроскопа в Фурье-плоскости в диапазоне наблюдаемых воздушных мод излучения для следующих значений γ: кривая 1 – 1.479, кривая 2 – 1.525, кривая 3 – 1.556, кривая 4 – 1.571 (при этом соответствующая толщина волновода имеет размер: h = λ/5, λ/2, λ, 3λ/2). Динамика диаграмм рассеяния при изменении γ достаточно очевидна. Параметры эффективных неровностей (модельных микрообъектов) здесь имеют значения: σ = 5 нм (≈ λ/120) и r = 10 нм (≈ λ/60). Отметим, что с возрастанием величины радиуса корреляции диаграммы рассеяния становятся асимметричными: их левая часть (относительно центра Фурье-плоскости при β = 0) уменьшается по амплитуде [8]. Диаграммы рассеяния волноводной моды на объемных неоднородностях волноводного слоя подобны приведенным на рис. 2, но имеют менее изрезанный характер по краям в области излучательных мод подложки волновода.
Рис. 2. Двумерные диаграммы рассеяния (функции отклика) волноводного оптического микроскопа в дальней зоне. Величина отношения сигнала к шуму около 10.
Для сравнения укажем размеры некоторых типичных микрообъектов в биомедицине и экологии (см., например, [21]). Вирус табачной мозаики: длина ~ 0.3 мкм, толщина ~ 40 нм. Вирус мозаичной болезни картофеля: длина ~ 0.5 мкм, толщина ~ 40 нм. Вирус гриппа: диаметр ~ 0.12-0.15 мкм. Бактериофаги: длина ~ 0.1-0.17 мкм, толщина ~ 10-70 нм. Размер молекулы гемоглобина составляет примерно 25-30 Å. Эритроциты и тромбоциты крови человека имеют длину примерно 1-5 и 5-8 мкм соответственно. Staphylococcus aureus имеют средний размер около 1 мкм. Микрочастицы (аэрозоль, пыль и др.) различного происхождения и состава имеют субмикронные размеры порядка 0.001-0.5 мкм. Таким образом, размеры многих из данных микрообъектов различной природы вполне удовлетворяют параметрам рассматриваемых в данной работе эффективных нерегулярностей. Последние, как сказано выше, обусловлены наличием статистического ансамбля модельных однотипных микрообъектов на границе волноводного слоя и кварцевых пластинок. Если подобные оптически прозрачные микрообъекты (не биологические или биологические), находящиеся в волноводном слое, рассматривать как объемные неоднородности, то среднеквадратичное отклонение показателя преломления от среднего значения близкое к используемому при моделировании имеют, например, следующие структуры (жидкий волноводный слой–модельные микрочастицы): 1) стирол–пыльца растений: Δn ≈ 0.15; 2) анилин–ПММА: Δn ≈ 0.13; 3) кедровое масло–клетки крови: Δn ≈ 0.17; 4) глицерин–клетки крови: Δn ≈ 0.12; 5) кедровое масло–Staphylococcus aureus: Δn ≈ 0.1.
Детальный анализ особенностей решения задач волноводного рассеяния при обоих типах задания модельных сред (в виде эффективных поверхностных неровностей или объемных неоднородностей) не представляет интереса для широкого круга специалистов биофизиков, медиков, биологов, экологов и др. и выходит за рамки данной работы.
4. ОБРАТНАЯ ЗАДАЧА ВОЛНОВОДНОЙ ОПТИЧЕСКОЙ МИКРОСКОПИИ
Решение обратной задачи при исследовании статистического ансамбля микрообъектов заключается в восстановлении ФСП и/или АКФ и определении соответствующих параметров микрообъектов по данным, полученным, например, в ближней, промежуточной или дальней зоне волноводного оптического микроскопа.
Восстановление автокорреляционной функции. При регистрации интенсивности рассеянного на эффективных неровностях (или оптически прозрачных микрообъектах, распределенных внутри волноводного слоя) излучения в дальней зоне точечным фотодетектором приближенное корректное решение обратной задачи может быть найдено с использованием процедуры квазиоптимальной регуляризации [6, 9, 15, 16, 19]. Восстановленная сглаженная автокорреляционная функция Ri(u,γ) находится из диаграммы рассеяния в дальней зоне (1) по следующей формуле:
где Ф* – комплексно сопряженное к Ф; μ – параметр регуляризации; M = β2p или M = (β0 - β)2p, p ≥ 0 – порядок регуляризации. При Мs = μ-1(SNR)-1 формула (4) дает оптимальное регуляризованное решение обратной задачи, которое совпадает с результатом применения оптимальной фильтрации по Винеру [23]; SNR – отношение сигнала к шуму. Сглаживающая функция E(u, β) квазиоптимального фильтра подбирается из условия минимума, например, среднеквадратичной ошибки восстановления АКФ [15, 16, 19].
В тех случаях, когда восстановление сглаженной автокорреляционной функции выполняется на дискретном множестве, используется формула:
где n = 0, 1, 2 … N, m = 0, 1, 2 … M, причем числа N, M << ∞ т.к. ограничены сверху точность вычислений на компьютере и уровнем заданного шума; un = n∙Δu; βm = m∙Δβ. В экспериментальных исследованиях достаточно ограничиться конечным числом слагаемых (5).
Разложение (5) может быть применено для решения поставленной обратной задачи с использованием известной теоремы отсчетов (теорема Уиттекера-Котельникова-Шеннона [4, 15]). Действительно, определяемый в соответствии с (1) спектр нерегулярностей является естественным образом ограниченным по протяженности, поэтому АКФ может быть определена по ее значениям в последовательности равноотстоящих точек или отсчетов un.
Используя разложение ФСП в ряд Тейлора, получим в результате формулу для аналитического продолжения спектра за пределы области регистрируемых мод излучения:
где N – число коэффициентов разложения, которое обычно ограничено сверху точность вычислений на компьютере и уровнем заданного шума; Fm = F(βs) = <P(βs, γ)∙Ф-1(βs, γ)>(m) – коэффициенты разложения, вычисляемые в некоторой точке βs
(-β3, +β3), β3 = kn3; верхний индекс m означает m-ю производную.
Формула (6) позволяет продолжить ФСП выше граничной пространственной частоты, используя, в том числе и аналитическое продолжение на комплексную плоскость до целой функции экспоненциального типа в соответствии с теоремой Винера-Пэли. Это позволяет повысить разрешение при решении обратной задачи волноводного рассеяния: точность восстановления ФСП и АКФ, и соответственно, точность определения параметров нерегулярностей [16].
Так, при экстраполяции спектра за пределы области измерения на величину диапазона наблюдаемых подложко-покровных мод излучения (т.е. расширение области определения ФСП вдвое) при уровне SNR ≈ 10 и N = 5 ошибка восстановления ФСП не превосходит 100%. Заданная гауссова автокорреляционная функция при этом восстанавливается с ошибкой менее 60%, а субволновые радиусы корреляции λ/15 — λ/35 могут быть определены с относительной ошибкой около 5-15% (см., например, [19]).
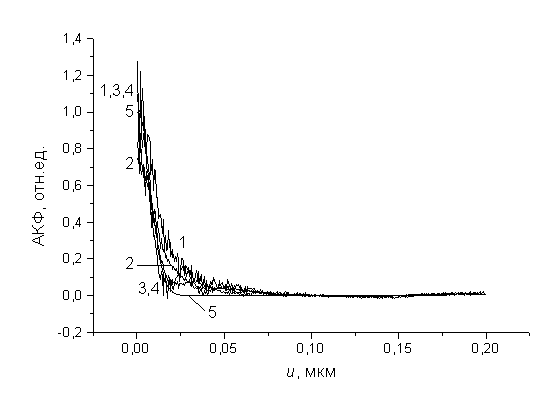
При численных расчетах на компьютере варьировались как функции Мs, E, так и параметры μ, p и γ. На рис. 3 приведены: заданная (кривая 5) гауссова АКФ — B(u) и восстановленные (кривые 1-4) из диаграмм рассеяния (приведенных на рис. 2) АКФ — Ri(u, γ) для функций Мs = (β0 - β)2p, E(u, β) = sin(muβ)/(muβ).
Определение геометрических параметров эффективной неровности поверхности. Геометрия поверхности может быть в общем случае достаточно сложной. У плоских образцов с поверхностью высокого класса чистоты неровность поверхности определяется главным образом статистической неровностью. Это будет вполне справедливо и при случайном распределении, например, ансамбля однотипных биологических микрообъектов на ровной поверхности (или в объеме волноводного слоя). При изучении таких ансамблей обычно используется гауссов (нормальный) закон распределения, зависящий только от двух параметров [23]: радиус корреляции r и среднеквадратичной высоты σ.
Рис. 3. Заданная (кривая 5) и восстановленные (кривые 1-4) из диаграмм на рис. 2 автокорреляционные функции при параметрах задачи: μ = 0.02, p = 0.02, m = 25.
Определение радиуса корреляции эффективной стационарной модельной неровности (и объемных неоднородностей) производилось по следующим четырем формулам:
где R(u) – нормированная автокорреляционная функция, восстановленная по формуле (4) из зашумленных диаграмм рассеяния. В качестве экспресс методики при экспериментальных исследованиях может быть использована оценка радиуса корреляции по характерному уровню e-1 ≈ 0.37 из восстановленных нормированных автокорреляционных функций Ri(u, γ). Радиус корреляции характеризует некоторый пространственный интервал ∆u, на котором корреляционная связь между значениями статистического процесса (в данном случае это – АКФ) "распадается". Можно понимать под радиусом корреляции некоторый латеральный размер неровностей поверхности, сопоставимый с параметрами принятыми в оптической микроскопии и метрологии.
Для заданной гауссовой АКФ с радиусом корреляции r = 10 нм (≈ λ/60) при использовании сглаживающей функции типа sin(mx)/mx с m = 25 были найдены следующие оптимальные параметры решения обратной задачи: μ = p = 0.02, γ = 1.571. Среднеарифметическое значение определенного радиуса корреляции отличается от заданного примерно на 8%.
При увеличении радиуса корреляции до 30 нм (≈ λ/20) можно восстановить АКФ с малой ошибкой при коэффициенте замедления γ = 1.556. Здесь среднеарифметическое значение определенного радиуса корреляции отличается от заданного на 6%.
При дальнейшем увеличении радиуса корреляции до 60 нм (≈ λ) возрастает ошибка восстановления АКФ и соответственно возрастает ошибка определения радиуса корреляции. Здесь среднеарифметическое значение может отличаться от заданного уже на ≈ 20-40%. Эта тенденция наблюдается при дальнейшем увеличении радиуса корреляции от λ до 15λ. В этом диапазоне значений радиуса корреляции удается снизить ошибку восстановления АКФ и определения r, например, за счет аналитической экстраполяции функции спектральной плотности за пределы области определения. Таким образом, точность восстановления АКФ, достигаемая с помощью предложенного алгоритма обработки зашумленных данных измерения в дальней зоне, является вполне достаточной для надежного определения радиусов корреляции эффективных неровностей в широком диапазоне значений.
Важно отметить, что ошибка определения радиусов корреляции ~ 15% равна примерно величине λ/200. Такая ошибка вполне удовлетворительна при решении многих экспериментальных задач, как в оптике, так и в биологии, биофизике, физхимии, экологии и др. Заметим также, что определение радиуса корреляции величиной около λ/30 формально соответствует превышению разрешения Аббе-Рэлея в классической оптической микроскопии в 15 раз. Таким образом, метод волноводного рассеяния, несомненно, позволяет решить проблему сверхразрешения в волноводной оптической микроскопии.
Среднеквадратичное отклонение эффективных неровностей поверхности от плоскости (среднеквадратичная высота) определялось по известным формулам:
где F(β, γ) – функция спектральной плотности, получаемая как Фурье-преобразование восстановленной АКФ. Использование восстановленной регуляризированной АКФ для определения среднеквадратичной высоты позволяет снизить ошибку определения σ по сравнению с формулой, использующей интегрирование функции спектральной плотности до ≈ 12-20% при SNR ≈ 1. При SNR ≥ 100 ошибка определения среднеквадратичной высоты эффективных неровностей менее 1-5%. Отметим, что аналогичным образом определяется среднеквадратичное отклонение показателя преломления волноводного слоя от среднего значения
оптически прозрачных микрообъектов, распределенных внутри волноводного слоя.
Теоретические оценки показали, что предельное разрешение метода ВОМ при высоком отношении сигнала к шуму составляет [5-7, 9]: по высоте – до 0.1Å; латеральное – до λ/30, а с дополнительной математической обработкой – до ≈ λ/60. При исследовании оптически прозрачных неоднородных микрообъектов (не биологических или биологических) среднеквадратичное отклонение показателя преломления от среднего значения может быть определено с точностью примерно 10-5-10-7, а соответствующий радиус корреляции «объемных» неоднородностей при дополнительной математической обработке – с точностью до ≈ λ/60. Дальнейшее развитие метода ВОМ требует проведения экспериментальных исследований с высоким отношением сигнал/шум в широком диапазоне мод излучения, формирующих оптический образ объекта, а также использования адекватной модели экспериментального шума.
В заключение важно подчеркнуть, что разработка методов повышения латерального разрешения является одной из фундаментальных задач не только оптики, но и естествознания в целом, поскольку ее решение уже в наше время позволило применить на практике вместо электронных микроскопов оптические (например, ближнепольные, конфокальные, гетеродинные и др. лазерные микроскопы), реализующие тот или иной неразрушающий способ получения in vivo субволнового "изображения" микрообъектов (см. например, [1-4, 15, 20]). Несомненно, решение этой задачи имеет большое значение в таких областях науки как оптика, биология, медицина, биофизика, экология и др.
5. ЗАКЛЮЧЕНИЕ
В данной работе представлен метод волноводной оптической микроскопии, основанный на явлении волноводного рассеяния когерентного излучения лазера, позволяющий восстановить автокорреляционную функцию эффективных статистических неровностей поверхности и/или неоднородностей объемного характера из зашумленных данных функции отклика волноводного оптического микроскопа. Разработанный метод может быть использован для исследования свойств статистических ансамблей микрообъектов различной природы и определения их статистических характеристик и параметров с превышением дифракционного предела Аббе-Рэлея.
Когерентная волноводная оптическая микроскопия может быть использована также при изучении структурных и функциональных изменений в ансамблях биологических микрообъектов, находящихся в жидкостном волноводном слое. Определение статистики и параметров микрообъектов (геометрических размеров и среднеквадратичного отклонения показателя преломления от среднего значения) может быть дополнено визуализацией соответствующих измерений с помощью ПЗС матрицы. При этом характеристики и параметры динамических процессов в ансамблях микрообъектов, полученные в результате волноводного рассеяния, несомненно, будут отражать особенности процессов самоорганизации и регуляции, как в самом ансамбле, так и в образующих его микрообъектах. Метод волноводного рассеяния в данном случае может позволить получить статистическую информацию о процессах в ансамбле биологических объектов за одно измерение с достаточно большой площади поверхности (объема) с превышением дифракционного предела, т.е. позволяет перейти в нанометровый диапазон. При этом волноводный оптический микроскоп выполняет роль высокопроизводительного интегрально-оптического когерентного Фурье-процессора.
ЛИТЕРАТУРА
Тычинский В.П. Микроскопия субволновых структур // УФН. 1996. Т. 166. C. 1219-1229.
Баранов Д.В., Егоров А.А., Золотов Е.М., Свидзинский К.К. Восстановление профиля микрообъекта в гетеродинном дифференциальном микроскопе // Опт. и спектр. 1997. Т. 83. С. 516-527.
Иваницкий Г.Р., Куниский А.С. Исследование микроструктуры объектов методами когерентной оптики. – М.: Энергия, 1981.
Аблеков В.К., Колядин С.А., Фролов А.В. Высокоразрешающие оптические системы. – М.: Машиностроение, 1985.
Егоров А.А. Волноводная сверхразрешающая микроскопия: приложение к биомедицинским и экологическим исследованиям // Тез. докл. VI-й Межд. науч.-техн. конфер. «Лазеры в науке, технике, медицине». 19-21 сентября 1995 г. Суздаль. М.: ИРЭ РАН. 1995. С. 67-69.
Egorov A.A. Theory of waveguide optical microscopy // Las. Phys. 1998. V. 8. P. 536-540.
Егоров А.А. Определение параметров статистического ансамбля микрообъектов в волноводном оптическом микроскопе // Изв. РАН. Серия Физическая. 1999. Т. 63. С. 1125-1131.
Egorov A. A. Optimization of characteristics and parameters of waveguide optical microscope // Las. Phys. 1999. V. 9. P. 542-547.
Egorov A.A. Waveguide optical microscopy // Proc. SPIE. 1997. V. 3200. P. 114-120.
Egorov A.A. Determination of the parameters of a statistical ensemble of microobjects in a waveguide optical microscope // Proc. SPIE. 1999. V. 3736. P. 375-384.
Егоров А.А. Методы контроля субмикронных структур и качества поверхности // Сб. науч. Трудов 2-й Науч.-техн. конфер. «Электроника, микро- и наноэлектроника». М.: МИФИ. 2000. С. 57-65.
Егоров А.А. Лазерные методы исследования микрообъектов с субволновым разрешением // Сб. науч. трудов РУДН. М.: РУДН. 2001. С. 378-384.
Егоров А.А. Волноводная оптическая микроскопия – новый лазерный метод исследования и контроля // Контроль. Диагностика. 2002. № 4. С. 25-30.
Егоров А.А. Модельный анализ волноводного рассеяния света на статистическом ансамбле биологических микрообъектов // Тез. докл. XIII-й Межд. науч.-техн. конфер. «Лазеры в науке, технике, медицине». 16-20 сентября 2002 г. Сочи. М.: МНТОРЭС им. А.С. Попова. 2002. C. 22-24.
Егоров А.А. Восстановление экспериментальной автокорреляционной функции и определение параметров статистической неровности поверхности по данным рассеяния лазерного излучения в интегрально-оптическом волноводе // Квантовая Электроника. 2003. Т. 33. № 4. С. 335-341.
Egorov A.A. Inverse problem of laser light scattering in an integrated optical waveguide: 2D solution with accurate input data // Las. Phys. 2004. V. 14. P. 1296-1309.
Egorov A.A. Theory of laser radiation scattering in integrated optical waveguide with 3D-irregularities in presence of noise: vector consideration // Las. Phys. Let. 2004. V. 1. P. 579-585.
Егоров А.А. Теория волноводного рассеяния света в интегрально-оптическом волноводе при наличии шума // Изв. Вуз. Радиофизика. 2005. Т. 48. С. 63-75.
Egorov A.A. Super resolution in the waveguide inverse light scattering problem // Journal of Radio Electronics. 2007. N 6.
Тычинский В.П. Когерентная фазовая микроскопия внутриклеточных процессов // УФН. 2001. Т.171. C. 649-662.
Вилли К., Детье В. Биология (Биологические процессы и законы). – М.: Мир, 1974.
Ахманов С. А., Дьяков Ю. Е., Чиркин А. С. Введение в статистическую радиофизику и оптику. – М.: Наука, 1981.