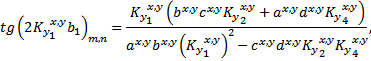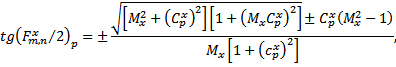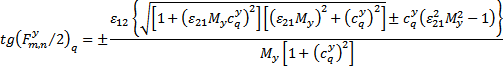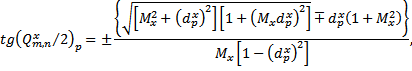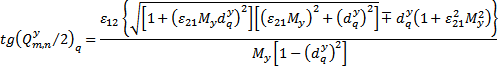Аномальная дисперсия волн, распространяющихся в многослойных металлодиэлектрических структурах

Б. А. Мурмужев, Р. Н. Денисюк

Институт Радиотехники и Электроники имени В. А. Котельникова РАН,
Фрязинский филиал

Получена 28 июня 2010 г.

Аннотация. Обнаружено, что дисперсионная характеристика одной из основных волн, распространяющихся в металлодиэлектрической структуре с двумя электромагнитно-связанными волноведущими слоями, имеет аномальную отсечку распространения на критической частоте, равной нулю, и величине относительного замедления, зависящего от геометрических и вещественных параметров структуры. Показана возможность применения такой структуры для создания широкополосных делителей высокого уровня мощности миллиметрового диапазона волн.

 

Ключевые слова: многослойные металлодиэлектрические структуры, аномальная дисперсия, делитель мощности, миллиметровый диапазон длин волн.

 

Введение.

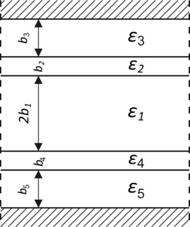
Многослойные плёночные структуры, содержащие волноведущие и разделительные слои (ВС и РС) диэлектриков или полупроводников, находят применение в функциональных элементах интегральной оптики [1,2 ]. В диэлектрических интегральных схемах миллиметрового диапазона [3] ВС или диэлектрические волноводы (ДВ) могут располагаться на поверхности металлической подложки с тонким промежуточным слоем (ПС) диэлектрика [4]. При формировании объёмной интегральной схемы [5] из двух расположенных друг над другом ВС или ДВ образуется пятислойная металлодиэлектрическая структура (МДС), содержащая расположенные между металлическими экранами (МЭ) два ПС, два ВС и РС (рис. 1). Такая МДС может быть использована для создания делителей мощности объёмного формообразования.

Рис. 1.

В направлении оси Z вдоль слоёв плоской (ширина ) МДС распространяются волны , отличающиеся направлением преимущественной поперечной поляризации электрического поля волны: волны  имеют компоненты поля , , и , а волны  - , , и . Индексы «m» и «n» означают число нечётных  и чётных  гармоник поля в ВС, а индексы «p» и «q» относятся к двум типам волн, соответственно имеющих нечётное  или чётное  гиперболические вариации поля по высоте РС. Именно электромагнитное взаимодействие волн  и  приводит к  биениям этих волн и перекачке электромагнитной энергии из одного ВС в другой и обратно [6].

 

1.    Дисперсионные уравнения.

Ранее в работе [7 ] для обобщённой модели МДС, содержащей расположенные между МЭ центральный ВС с диэлектрической проницаемостью  и высотой , два ПС с диэлектрическими проницаемостями  и  и высотами  и  с верхней стороны ВС и два ПС с диэлектрическими проницаемостями  и  и высотами  и  с нижней стороны ВС ()  было получено обобщённое дисперсионное уравнение (ДУ) для суперпозиции нечётных и чётных гармоник поля волн  по высоте  ВС и суперпозиции полей с экспоненциальным распределением амплитуды по высотам ПС . Это трансцендентное уравнение имеет вид:

(1)

 

где  - поперечные волновые числа,

Решение ДУ (1) значительно упрощается для симметричной МДС (рис. 1), в которой для двух ПС, контактирующих с ВС, поперечные волновые числа , а для двух ПС, контактирующих с МЭ .

В этом случае коэффициенты , , а ДУ (1) имеет два независимых решения для волн  и :

	(2)
	(3)

 

В данной работе рассматривается обратная дисперсионная задача, когда два ПС с высотами  и диэлектрическими проницаемостями  выполняют функции ВС с гармоническим распределением амплитуд полей, а ВС высотой  и диэлектрической проницаемостью  является РС, соответственно, с нечётным и чётным гиперболическими вариациями полей. При этом соблюдается соотношение

Для симметричной МДС с двумя ВС в ДУ (2) и (3) действительные значения поперечных волновых чисел  необходимо заменить на мнимые, то есть произвести подстановки . В этом случае в ДУ (2) и (3) происходит замена тригонометрических функций на гиперболические и, наоборот, гиперболических функций на тригонометрические, так как

Для решения ДУ (2) и (3) необходимо учесть соотношения между продольными  (постоянные распространения) и поперечными волновыми числами . Эти соотношения следуют из условий для разделения переменных в волновом уравнении Гельмгольца и имеют вид:

,

(4)

 

где  - волновое число в вакууме.

Для упрощения совместного решения уравнений (2) – (4) введём новые параметры , которые характеризуют отношения поперечных волновых чисел:

В этом случае с учётом соотношений (4) для нормированных к высоте ВС  поперечных волновых чисел получим:

	(5)

Где

.

Решения ДУ (2) и (3) совместно с выражениями (5) удобно записать относительно функций , характеризующих суперпозицию нечётных и чётных гармоник поля в ВС. Эти решения в параметрической форме имеют вид:

	(6)

 

	(7)

 

Где ,  ,  .

Следует заметить, что в предельном случае ,  пятислойная МДС трансформируется в открытый трёхслойный волновод, а система ДУ (7) для волн  соответствует ДУ для нечётной и чётной волн трёхслойного волновода [6]. Для получения ДУ нечётных  и чётных  волн системы уравнений (6) и (7) необходимо разрешить относительно функций  половинного аргумента. В этом случае системы ДУ (6) и (7) можно представить в обобщённом виде:

(8)

 

Знаки «+» и «-» в системах ДУ (6) и (7) относятся к ДУ для нечётных  и чётных волн .

Системы ДУ (8) характеризуют сложную функциональную связь параметров , пропорциональных приведённым волновым числам  (частоте), с параметрами , равных отношению поперечных волновых чисел, а также с геометрическими  и диэлектрическими  параметрами МДС.

Действительные решения систем ДУ (8) существуют при изменении параметров  в пределах . Левый предел  соответствует низкочастотным границам спектра волн , а условия  определяют высокочастотную границу спектра волн .

Относительное замедление волн  определяется из уравнений (4) и в параметрической форме имеет вид:

(9)

 

Из выражения (9) следует, что изменение параметров  в пределах  ограничивает спектр волн  пределами относительных замедлений .

В случае, когда параметры , расчётная пятислойная модель МДС на рис. 1, трансформируется в две плоские пластины с высотой  и диэлектрической проницаемостью , окружённые безграничными средами с диэлектрическими проницаемостями  и . При этом аргументы гиперболических функций  и , гиперболические функции  и , а уравнения в системе ДУ (8) вырождаются и при  имеют известный [8] вид:

При  параметры , а уравнения в системе ДУ (8) имеют явные решения:

, .

Эти решения означают, что при относительном замедлении  спектр основных и высших типов волн  не ограничен по приведённым волновым числам  (частоте).

Спектральный анализ систем ДУ (8) в общем виде затруднён. Однако, для основных волн  возможны решения  и, следовательно, . Проверка возможности таких решений показала, что основные волны  и  при любых значениях параметров  и  имеют решения  и  Аномальным исключением является ДУ для основной волны , которое при  и, следовательно,  имеет конкретное решение для параметра  в виде:

(10)

 

Из выражения (10) следует фундаментальный вывод о том, что в симметричной пятислойной МДС основная волна  имеет критическую отсечку распространения по относительному замедлению , которое зависит от вещественных и геометрических параметров МДС и находится в интервале  при частоте .

В другом предельном случае, когда параметры , решения уравнений в системе ДУ (8) соответствуют низкочастотной отсечке распространения волн  и  при относительном замедлении  и приведённых волновых числах   и . Приведённые волновые числа для критических частот основных типов волн  и  соответствуют условиям  и .       

При фазовом синхронизме волн  и  должно происходить вырождение дисперсионных характеристик (ДХ) и, следовательно, ДУ в систему ДУ (8) для этих волн. В этом случае параметры , , , а равенства правых частей уравнений для волн  и  приводят к условиям:

(11)

 

Из выражения (11) следует, что ДХ волн  и  не имеют общей точки пересечения (точки кроссовера), а полный фазовый синхронизм этих волн при конечных значениях параметра  наступает при  и, следовательно, условиях

Следует отметить, что эффективность взаимодействия волн  и  повышается при увеличении относительного расстояния  между ВС.

2. Аномальная дисперсия основных волн .

Для частного случая  и , параметры , , а система ДУ (6) упрощается и имеет вид:

	(12)
	(13)

 

Из систем ДУ (12) и (13) видно, что ДУ для волн  и  имеют независимые от параметров  и  решения при  и  в виде  и .

Эти решения означают, что дисперсионные кривые (ДК) основных волн  и  для различных значений  имеют при относительных замедлениях   и приведенных волновых числах ,  общую точку пересечения. Низкочастотная отсечка распространения волн  и  при  соответствует относительному замедлению   и приведённым волновым числам  и . Аномальным исключением является волна , которая согласно первому уравнению системы ДУ (8) имеет отсечку распространения  при  и относительном замедлении

(14)

Из выражения (14) следует, что отсечка распространения основной волны  происходит при критической частоте, равной нулю и относительном замедлении, зависщем не только от вещественных, но и геометрических параметров симметричной МДС. Указанный эффект очевидно связан с конечной величиной электростатической энергии волны , запасённой в образованном МДС конденсаторе с многослойным диэлектрическим заполнением.

3. Волноводные моды.

Последовательный набор волноводных мод при  обусловлен распространением в МДС волн, имеющих гармонические распределения амплитуд полей в ВС, РС и ПС. Для первых волноводных мод в системе ДУ (8) необходимо действительные значения параметров  заменить на мнимые, то есть произвести подстановку .  При такой подстановке происходит изменение параметров в системе ДУ (8), а также преобразование гиперболических функций в тригонометрические, так как , где

Решение системы ДУ (8) для вторых волноводных мод соответствует мнимым значениям параметров  Изменение параметров  в системе ДУ (8) определяется высокочастотной границей спектра, соответствующей условиям  и относительному замедлению  Низкочастотная граница спектра первых волноводных мод соответствует условиям  и, следовательно , , и .

В области замедлений  происходит распространение вторых волноводных мод. Эти замедления соответствуют изменению параметров  в пределах .

При  постоянная распространения становится мнимой величиной, что соответствует преобразованию спектра волноводных мод в реактивные запредельные волны.

Для частного случая  и  системы ДУ (12) и (13) для волноводных типов волн при  преобразуются к виду:

	(15)
	(16)

 

Следует заметить, что первое уравнение системы ДУ (15) для волноводных мод  и последнее уравнение системы ДУ (16) для волноводных мод  при  и  имеют независимые решения для нечётных и чётных мод:

Из полученных решений следует, что чётные волноводные моды  и  имеют низкочастотную отсечку распространения при условиях  и  

Аномальными являются спектральные характеристики волноводных мод  и . Это связано с тем, что при  ДУ для этих волн соответствуют преобразованию нечётных волн  в волноводные чётные моды  и, наоборот, чётных волн  в нечётные волноводные моды .

4. Численные результаты.

Численный анализ систем ДУ (15) и (16) проводился для симметричной пятислойной МДС с параметрами:  (полиэтилен),  (высокоомный кремний), . Из уравнений при заданных параметрах ,  и  определялись приведённые волновые числа  для двух основных волн  и двух высших волн   при известных значениях ,  и  из выражений (9) и (14) определялись относительные замедления этих волн в зависимости от приведённых волновых чисел (частоты).

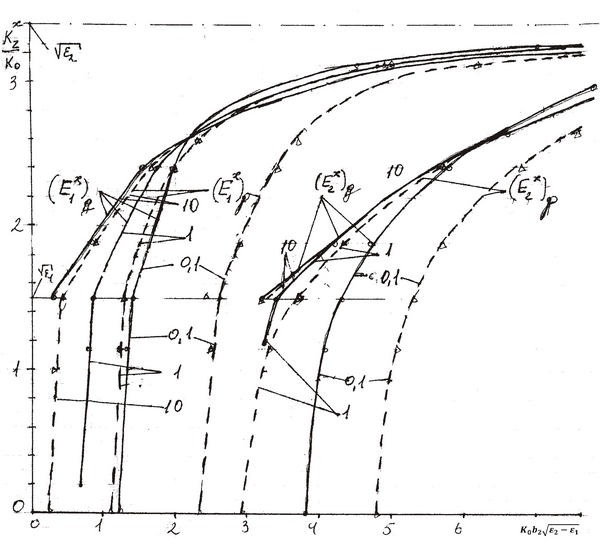
На рис. 2 показаны дисперсионные кривые (ДК) волн  (сплошные кривые) и волн  (штриховые кривые) при . Интервал относительных замедлений  соответствует границам спектра волн , а в интервале относительных замедлений  расположены ДК волноводных мод. Видно, что волны  имеют низкочастотную отсечку распространения при  и относительном замедлении . При  , и относительном замедлении  происходит пересечение ДК волн  при различных значениях параметра . Видно, что увеличение  приводит к сдвигу критических частот в сторону меньших значений  и к сближению ДК волн  и . Для волноводных мод ДК являются продолжением в область замедлений  ДК волн . При этом критические частоты волноводных мод  зависят от параметра  и имеют относительные замедления  при .

Рис. 2.

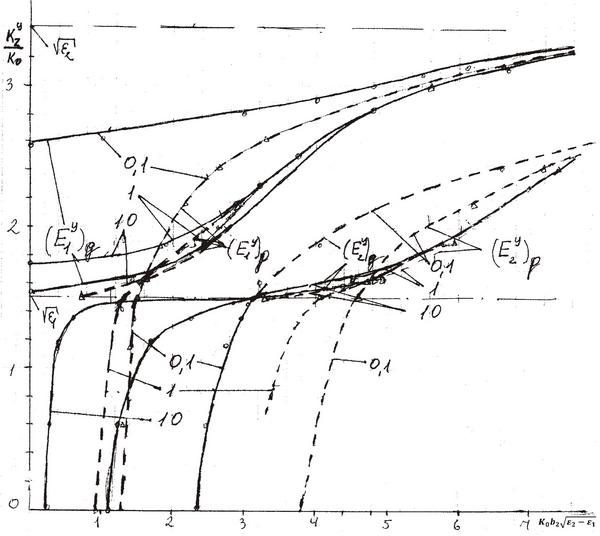
Рис. 3.

 

На рис. 3 представлены ДК волн  и  (соответственно, сплошные и штриховые кривые) для . Видно существенное аномальное различие ДК основных волн  и  (рис. 2). Это различие заключается в том, что основная волна  имеет критическую частоту при  и величине относительного замедления , в то время как основная волна  имеет критические частоты при  и .

При этом уменьшение параметра  приводит к смещению критических замедлений волны  в сторону больших значений   Критические частоты основной волны  так же как и волны  на рис. 2, зависят от параметра  и соответствуют условиям >0 при . Все ДК волны  при  и =1,62 и различных  имеют общую точку пересечения. При увеличении  происходит сдвиг критических частот волн  в сторону меньших значений  и сближение ДК волн  и . При этом практическое вырождение ДК этих волн происходит при более низких значениях , чем для волн  и . Это означает, что эффективное электромагнитное взаимодействие волн  и  происходит в более широкой полосе частот.

Спектр волноводных мод  расположенный на рис. 3 в диапазоне относительных замедлений , имеет аномальные свойства, заключающиеся в том, что спектр нечётных волн  при  преобразуется в спектр чётных волноводных мод, а спектр чётных волн  трансформируется в спектр нечётных волноводных мод . Поэтому ДК волноводных мод  являются продолжением в область относительных замедлений  ДК волн . Следует заметить, что ДК волноводной моды  не имеют аномальных свойств, а критические частоты волноводной моды  смещаются в область замедлений

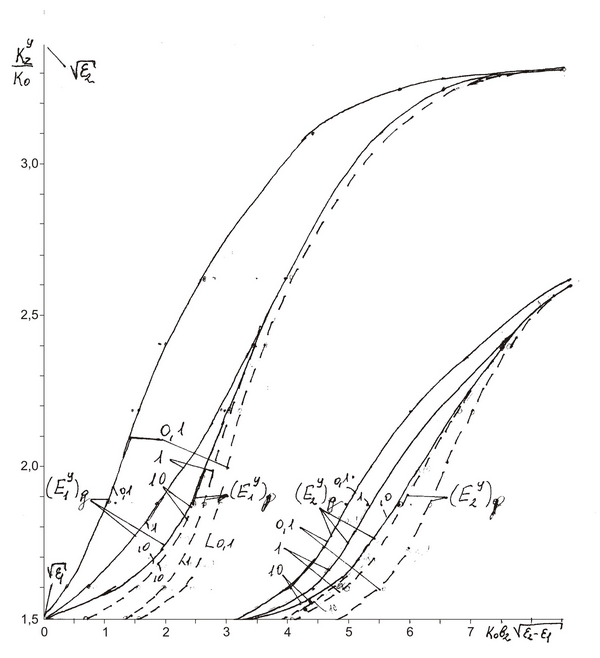
Рис. 4.

В открытой структуре (рис. 4) при отсутствии МЭ существенным образом изменяются ДХ волн  (сплошные кривые) и  (штриховые кривые). Видно, что в отличие от пятислойной МДС (рис. 3) в открытой трёхслойной структуре критическая частота основной волны  не зависит от параметра  и соответствует приведённому волновому числу  и относительному замедлению . При этом ДК волн  при различных  не имеют общих точек пересечения и при увеличении  сдвигаются в сторону меньших значений .

Заключение.

Наличие МЭ в многослойной МДС с двумя ВС приводит к аномальной дисперсии основных волн  Эти аномальные эффекты заключаются в наличии общей точки пересечения ДК волн  и  при различных значениях параметра , а также в наличии критических относительных замедлений волны  при  и  Кроме того, при  наблюдается эффект преобразования нечётных волн  в чётные волноводные моды

Установлено, что увеличение относительного расстояния  между ВС приводит к сближению ДК волн  и , а практическое вырождение ДК волн  и  наступает при меньших значениях приведенных волновых чисел, чем для волн  и   Это увеличивает широкополосность делителей мощности, использующих распределённую электромагнитную связь волн  и  в пятислойной МДС.

 

ЛИТЕРАТУРА

1.    Введение в интегральную оптику. Под редакцией М. Барноски. Перевод с английского под ред. Т. А. Шмаонова. Издательство Мир, М. 1977.

2.    Гвоздев В. И., Мурмужев Б. А., Подковырин С. И. // Микроэлектроника, 1998, т. 24, № 4, с. 244.

3.    Взятышев В. Ф., Нарытник Т. Н., Рябов Б. А. //Обзоры по электронной технике. Сер. 1. Электроника СВЧ. 1986. Вып. 13 (1209).

4.     Вапнэ Г. М., Глаголев Б. С. //Обзоры по электронной технике. Сер. 1. Электроника СВЧ. 1986. Вып. 11 (1200).

5.    Гвоздев В. И., Нефёдов Е. И. Объёмные интегральные схемы СВЧ. М. 1985.

6.    Мальцев В. П., Нефёдов Е. И., Шевченко В. В. //Известия Вузов. Радиоэлектроника, 1970, т. 13, №11, с. 1381.

7.    Мурмужев Б. А. // РЭ. 2005, т. 50, №7, с. 849.

8.    Взятышев В. Ф. Диэлектрические волноводы, М. 1970.