Waveguide light scattering method as a best way for research of the statistic irregularities of integrated-optical waveguides
A. A. Egorov
A.M. Prokhorov’ General Physics Institute, Russian Academy of Sciences
Received June 21, 2010
Abstract. The phenomenon of the waveguide light scattering in the irregular planar integrated-optical waveguide is investigated. The solution of the direct scattering problem is fined with the help of the theory of perturbations. The inverse waveguide scattering problem consists in restoring of spectral density function and/or autocorrelation function of waveguide’s irregularities and determination of irregularities’ parameters by the measuring data of radiating field in the far zone. The computer simulation and experimental results allow approving, that our method permits to receive an approximate correct solution of the inverse scattering problem with the rms error of restoring of the given autocorrelation functions no more than 35% in the presence of high real noise (for SNR ≥ 1). The statistic parameters of irregularities in this case are determined with the error less than 15-30 %.
Keywords: integrated optics, waveguide, irregularities, waveguide scattering phenomenon, autocorrelation function, noise, computer modeling, incorrect scattering problem.
1. Introduction.
The intensive development of the integrated optics and optoelectronics during last 30 years promoted the researches of the light scattering in the irregular optical waveguides (OWG) from the different points of view [1-14]. As it is known the integrated optical waveguide is one of basic elements of the integrated optics. In most cases integrated OWG serves as the basis for creation of the various optical integrated circuits. In this connection the important direction in technology is the development of methods of creation of an OWG with a low level of losses of the intensity of a directed mode on scattering on irregularities (boundaries roughness and heterogeneities of the waveguide layers) of the structure of a waveguide.
The laser light scattered in an OWG can be registered as radiated substrate-cover (substrate-air) and substrate modes (“out-of-plane scattering”), and as the radiation, scattered in the plane of a waveguide (“in plane scattering”). The main task in all cases consists in a correct solution of the direct and inverse scattering problems [8-14, 17-19].
As a rule, when analyzing the light scattering the authors give main attention to the solution of the direct scattering problem i.e. to the determination of the field's or to the intensity's characteristics of the coherent radiation scattered in the waveguide. The found scattering diagrams (patterns) then are used for the solution of an inverse problem by the known comparison method, when one tries by that or different way to achieve the coincidence, for example, by the least squares method (in rms sense) of the experimentally measured diagrams with the theoretically calculated one. When the irregularities are statistical, the diffraction spectra are diffused, and instead of the sum of final number of the plane waves there is an integrated expansion of the field in each point by the plane waves [2, 9-14]. If the conditions of the waveguide mode scattering on the statistical ensemble of microobjects (it can be the statistical roughness of the surface or statistical heterogeneity of the refraction index of the waveguide layers) satisfy to the first approximation of the theory of perturbations, the intensity of the scattered radiation, registered by the “dot” photodetector in the far zone or in an equivalent Fourier plane, is actually a map of the spectral density function (SDF or the power spectrum density (PSD) function) in the space of the wave numbers. As is known, in this case the scattering depends only on the statistical characteristics of the second order of an ensemble of microobjects: SDF or its Fourier-transformation i.e. the autocorrelation function (ACF) [20-30].
The ACF and SDF contain all the information about main parameters of the researched ensemble of microobjects. In considered case the first approximation of the perturbations theory is satisfied, if the root-mean-square (rms) height of the boundaries roughness of OWG is small on a comparison, both with the wavelength of the laser radiation, and with the thickness of the waveguide layer.
In this paper the phenomenon of the waveguide scattering in the irregular planar optical waveguide is investigated. The solutions of the direct and inverse waveguide scattering problems are fined. The computer modeling of both problems are presented.
2. Physical nature of problem. Theoretical analysis of the waveguide light scattering problem.
The phenomenon of waveguide light scattering is being examined in two main directions. The first direction includes the general theory of irregular planar optical waveguide, peculiarity of process of intermode waveguide scattering (mode conversion) etc. In the second direction phenomenon of waveguide scattering is used for investigation of the irregularities properties themselves and determination of their characteristics and parameters. This division can't be very strict because two aspects of problem are being carried on in the examination [1-14, 17-30].
In this paper the out-of-plane two-dimensional (2D) scattering in the incident plane is considered. Let's consider the scattering of the incident waveguide mode in the integrated optical waveguide containing the statistical three-dimensional (3D) irregularities. When neglecting polarizing effects the problem of waveguide three-dimensional (3D) scattering [9, 21, 23, 24, 26] is reduced to the solution of the known two-dimensional wave equation [12-14].
Then we assume absence of the cross-correlation connections between all types of irregularities (roughness of the boundaries and/or heterogeneity of the layers of OWG) [18]. The solution of the inverse problem is reduced to the restoration of the autocorrelation function of the statistic stationary irregularities of the planar optical waveguide by the data of the light scattering in the far zone (or in the equivalent Fourier-plane).
The new algorithm of the solution of the inverse waveguide scattering problem is used which is the combination of the classic (Tikhonov’s) [15] regularization and the quasi-optimal (Egorov’s) filtration of the measured data [12-14, 18-20, 22-25, 27-29].
The planar optical waveguide usually consists of three layers (Fig. 1): the cover medium, thin waveguide layer and the substrate with the refraction indexes n1, n2 and n3 accordingly. The imperfections of the structure of OWG can be stipulated by the irregularities (roughness) of the boundaries of the unit of the mediums forming the waveguide, the under surface defects (so-called infringed or cracked layer) and the heterogeneities of the refraction index of the waveguide layers.
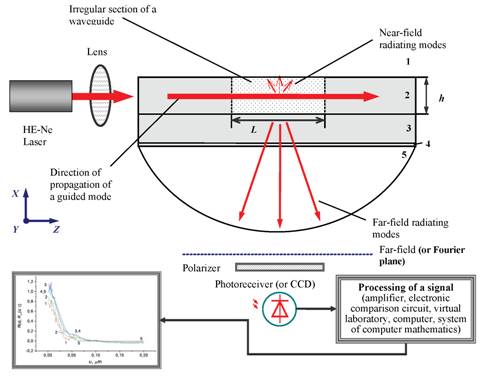
Fig. 1. Scheme of light 2D-scattering in the irregular asymmetric planar optical waveguide: 1 is the covering layer, 2 is the guiding layer, 3 is the substrate, 4 is an immersion, 5 is the quartz hemisphere, 6 is the lens, h is the waveguide thickness, L is the length of the irregular region.
The heterogeneities of the waveguide layers and under surface defects during the consideration of the scattering problem can be circumscribed of the same type as the heterogeneities of the refraction index of the appropriate waveguide medium. For simplification of the theoretical analysis of the waveguide scattering problem we shall neglect cross-correlation connections, both between irregularities of the boundaries of the unit, and between irregularities of the boundaries and heterogeneities of the refraction index of waveguide mediums.
In the Fig. 1 the scheme of light scattering in the irregular OWG is presented, where L is the length of area containing the statistical irregularities, h is waveguide thickness, the cover medium 1 and substrate 3 have the same refraction indexes, 4 is the immersion, 5 is the quartz semi sphere, PD is a photodetector, P(β, γ) is the intensity of scattered light, ADC is analog-to-digital-converter, PC is a personal computer.
On the Fig. 2 the diagram of the wave
numbers β and ρ are presented ![]() , k = 2π/λ,
i = 1, 2, 3; K is a certain harmonic lattice vector in the
infinitive spectrum of the irregularities; θ is the scattering
angle in the xz plane of incidence.
, k = 2π/λ,
i = 1, 2, 3; K is a certain harmonic lattice vector in the
infinitive spectrum of the irregularities; θ is the scattering
angle in the xz plane of incidence.
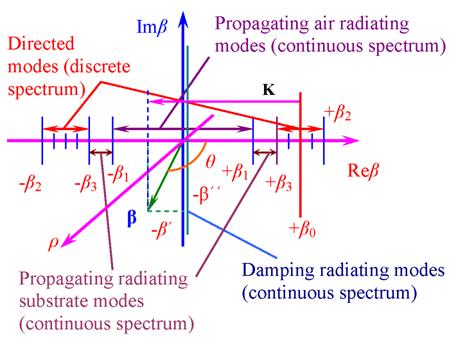
Fig. 2. Wave numbers diagram of an asymmetric optical waveguide.
The problem of scattering of the guiding mode in the planar optical waveguide containing stochastic irregularities (Fig. 1) is solved with the help of the theory of perturbations [2, 8-14]. A solution is sought for in the form of an expansion of an arbitrary radiation field distribution in terms of OWG orthogonal TE or TM modes [10, 12, 18]. We will consider the case of the guiding TE-mode scattering in the irregular OWG.
3. Direct waveguide 2D-scattering problem. Main equations. Numeric modeling
3.1. Formulation of a direct waveguide 2D-scattering problem
The solution of the direct 2D-problem consists in the determination of the scattering diagram, mainly in the near or far zone (or in an equivalent Fourier-plane) [8-14]. In the case of the statistical irregularities it is more preferable to measure intensity of the scattering diagram in the far zone with the help of the point (dot) photo receiver.
When the statistic surface roughness is under consideration there is no separation of the scattered plane waves and we should write the scattered intensity <P> in the integral form (integrated scattering problem) [12-14]:
![]() ,
(1)
,
(1)
where β is the longitudinal component of the propagating constant of scattering modes forming an optical pattern of irregularities; C0 is the normalized coefficient (or so-called wavelength factor); D(β', β) is the transfer function of photo detector; Ô(β'; γ) is the optical transfer function (OTF) of the waveguide (waveguide optical factor); F(β'; γ) is the spectral density function of the statistical irregularities (irregularities factor); γ is the effective refraction index of the waveguide; <…> means averaging on an ergodic ensemble of statistically identical systems.
When the point photoreceiver is used (D(β', β) is delta function δ(β' - β)) the far zone scattering diagram <P(β; γ)> can be presented as for the differential scattering problem:
For investigation of the direct and
inverse waveguide scattering problems the model statistic (e.g. non-sinusoidal)
noise is taken in the form of the band-limited additive (+ in Eq. (3)) or
multiplicative (one should use ![]() in Eq. (3) instead of
in Eq. (3) instead of ![]() ) “white” noise W(β;
γ) [12-17], therefore the equation Eq. (2) must be written in the
form:
) “white” noise W(β;
γ) [12-17], therefore the equation Eq. (2) must be written in the
form:
The intensity of the “white” noise W(β; γ) in Eq. (3) is generated as the uniformly distributed random number between 0 and ξ (ξ is real and depend on the SNR level).
3.2. Numeric modeling of direct waveguide 2D-scattering problem for the surface roughness
The computer modeling of the direct waveguide scattering problem is conducted as an example for the stationary statistical roughness of the surface of quartz plates (index of refraction n1 = n3 = 1.46 for λ = 0.63 μm (helium-neon laser)), between which there is thin optically transparent liquid layer (n2 = 1.59) without losses.
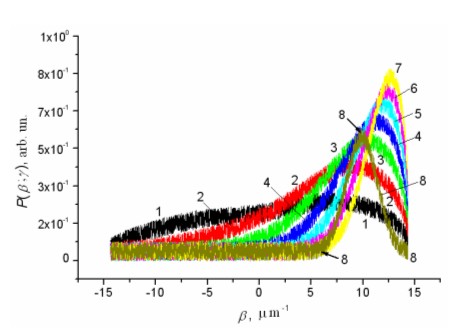
The scattering patterns for the given
Gaussian spectral density function ![]() with rms height σ = 5 nm and
different correlation radiuses (intervals) are depicted accordingly on the Fig.
3; β0 = kγ, and γ ≈ 1.48 in all cases. The scattering patterns
are calculated for the substrate-cover and substrate radiating modes intervals:
with rms height σ = 5 nm and
different correlation radiuses (intervals) are depicted accordingly on the Fig.
3; β0 = kγ, and γ ≈ 1.48 in all cases. The scattering patterns
are calculated for the substrate-cover and substrate radiating modes intervals:
![]() , where
, where ![]() . In all cases here SNR
≈ 10.
. In all cases here SNR
≈ 10.
Fig. 3. Theoretical Gaussian (curves 1-7) and experimental (curve 8) scattering diagrams of a laser radiation in the far-field zone in the plane of incidence (xz). Theoretical Gaussian curves 1-7 are obtained for the following parameters of the roughness: σ = 5 nm, and the correlation interval r is changed from 0.05 till 0.35 micron with the step of 0.05 microns.
Fig. 4 shows the calculated SDF of the band-limited “white” additive noise (for one realization) that is used during computer simulation of the process of restoration of the given theoretical autocorrelation functions via Eqs. (7) and (8). The imaginary part of SDF is calculated for verification during the computer simulation that the used noise statistic process is the real process.
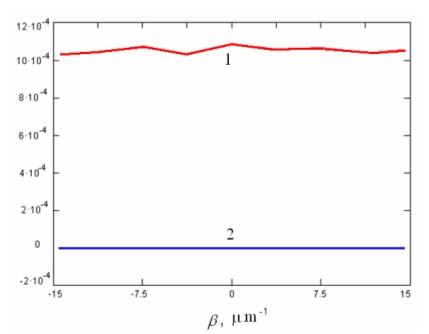
Fig. 4. SDF of the real “white” noise (for one of the noise realizations): 1 is the real part and 2 is the imaginary part in arbitrary units.
The autocorrelation function of the test roughness B(u) is being Fourier-transformation of the given Gaussian SDF: B(u) = σ2exp[-(u/r)2]. The parameters take the values: root-mean-square height σ = 0.1-50 nm (1-500 Å) and correlation radiuses r = 0.01-10 μm. It is supposed, that the studied surfaces are treated by same procedure and belong to one ergodic ensemble, therefore determined statistical characteristics and parameters of the surface roughness i.e. ACF, PSD, rms height and correlation interval are identical to the roughness of both boundaries of the waveguide. The dynamic of the calculated scattering patterns in the presence of the additive or multiplicative band-limited “white” noise as the correlation interval and effective index of refraction change is obvious. The same dynamic has been obtained for others types of the planar optical waveguides and different statistics of the irregularities. It should be noted that e.g. the scattering patterns for the exponential ACF with different correlation intervals are more asymmetric than the patterns on the Fig. 3 (curves 2, 3), so that the left part of the patterns tends to the zero level like on the Fig. 3 (curves 5-7).
The computer modeling of the guiding mode scattering problem on the heterogeneities of the waveguide layer can be conducted similar as for the surface roughness. Here we should consider that there are no losses due to the surface roughness and there are losses due to the heterogeneities of the waveguide layer (liquid with n2 = 1.59). Note that the scattering patterns for the specified Gaussian ACF are similar to the curves depicted on the Fig. 3.
4. Waveguide 2D inverse light scattering problem. Main equations. Algorithm of a solution for the high statistic noise
The solution of the inverse problem for
the statistic ensemble of irregularities consists in the restoration of the ACF
(and/or SDF) and the determination of the appropriate parameters of the
irregularities by the measuring data of the scattering diagrams (patterns) in
the far zone (or in the equivalent Fourier plane). Different procedures of
processing of the measured data can be used to obtain sufficient resolution in
the experiments. We use a new algorithm of processing of the data measured in
the far zone [13, 18-20]. First the spectral density function ![]() of the irregularities
is restored by the far zone data. Second SDF can be than expanded into the Taylor series and then it can be
extrapolated out of the range of the wave numbers β
of the irregularities
is restored by the far zone data. Second SDF can be than expanded into the Taylor series and then it can be
extrapolated out of the range of the wave numbers β ![]() (-β1,
+β1), where β1 = kn1,
of the registering scattering modes. Thereafter the algorithm that uses the
classic regularization and the quasi-optimal discrete data filtration processes
these data. Investigation of this algorithm by the computer modeling for
different types of the planar optical waveguides and different statistics of
the irregularities demonstrates that it is rather simple and permits to
eliminate efficiently the high additive band-limited “white” noise. After certain
modification it permits to eliminate the influence of the high multiplicative
band-limited “white” noise but not so sufficiently as the additive one.
(-β1,
+β1), where β1 = kn1,
of the registering scattering modes. Thereafter the algorithm that uses the
classic regularization and the quasi-optimal discrete data filtration processes
these data. Investigation of this algorithm by the computer modeling for
different types of the planar optical waveguides and different statistics of
the irregularities demonstrates that it is rather simple and permits to
eliminate efficiently the high additive band-limited “white” noise. After certain
modification it permits to eliminate the influence of the high multiplicative
band-limited “white” noise but not so sufficiently as the additive one.
4.1. Taylor expansion of SDF in presence of the statistic noise
We note that the formula Eqs. (2) and (3)
can be used for the solution both of the direct and inverse problems in the
spectral region but with the known space resolution limited by the range of the
observable scattering substrate-air and substrate modes β ![]() (-β1,
+β1) where β1 = kn1,
β1 = β3 [10-14]. The spectral
density function of the statistical irregularities restored from equation Eq.
(3) can be than expanded into the Taylor series [12-14]:
(-β1,
+β1) where β1 = kn1,
β1 = β3 [10-14]. The spectral
density function of the statistical irregularities restored from equation Eq.
(3) can be than expanded into the Taylor series [12-14]:
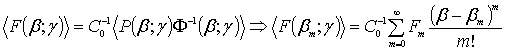 , (4)
, (4)
where m = 0, 1, 2 … ; βm = m∙Δβ; Fm = F(βm) = <P(βm; γ)w∙Ô-1(βm; γ)>(m) is the expansions coefficients taking in the reading (sample) points, the superscript index m means the m-th derivative.
The analytic extrapolation in the presence of the noise requires as is known the use of the regularization methods [8, 15]. In this case the Fourier-transformation of the formula Eq. (4) permit to write the next form for restored ACF R(u, γ):
![]() ,
(5)
,
(5)
where number m of expansion
coefficients determines the rms error of SDF’s and ACF’s restoration; ![]() ,
, ![]() . It can be shown that the
relative error of the rms height determination may be less than 1% for typical
planar waveguides when m ≥ 15 and there are not noise influences
on the registered far-zone data.
. It can be shown that the
relative error of the rms height determination may be less than 1% for typical
planar waveguides when m ≥ 15 and there are not noise influences
on the registered far-zone data.
The restored SDF can be extrapolated into the double band of the taking into account scattering modes with an error not grater than 100 % when the value of expansion coefficients m = 5 and SNR ≈ 10. The given Gauss ACF is determined then from Eq. (5) with an error less than 55 %. The correlation interval r from 20 nm to 3 μm of the given autocorrelation function in this case is determined with the relative error about 5-15 %. The described procedure permits to achieve certain super resolution over the parameters of the statistic irregularities under consideration.
4.2. Standard Tikhonov’s regularization and the quasi-optimal Egorov’s filtration of the measuring scattering noisy data
When the registration of the light scattered intensity is performed in the presence of the noise in the far zone by the point photo detector the evaluation of ACF R(u; γ) can be obtained from the noisy data as the Fourier-transformation of SDF Eq. (4). Then to this estimation of ACF the classic [15] regularization method [12-14, 17-21] can be applied:
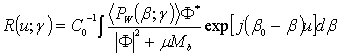 ,
(6)
,
(6)
where u = z - z', z and z' are coordinates in the plane of object, i.e. irregularities of OWG; β0 = kγ is the propagation constant of the waveguide mode; Ô is the optical transfer function of the waveguide (kernel of integral transformation), Ô* is the complex conjugate to Ô; μ is the regularization parameter; the elementary stabilizers of p-order are taken as M1 = β2p or M2 = (β0 - β)2p, p ≥ 0 is the regularization order, b = 1, 2.
The Eq. (6) allows receiving an approximate regularized solution of the inverse diffraction limited problem on Tikhonov [15]. For Ìb = μ-1(SNR)-1 formula (6) gives the optimum regularized solution of the inverse problem, which coincides the result of application of the optimum Wiener filtration [15]. As it is known the Wiener filter operates efficiently only when the spectra of the signal and noise do not overlap [16]. When the spectra are overlapped another procedure of filtering should be found. The equation Eq. (6) yields the solution of the inverse scattering problem in the planar optical waveguide with statistical irregularities of both types, both roughness of the boundaries, and heterogeneities of the refraction index in case of their additive contribution in the common scattering diagram. Note that the classic regularization method do not permit to achieve a superresolution over the parameters of irregularities.
It is known that in the far zone the scattering on roughness of the boundaries of the waveguide is mainly dominant [4]. Using the similar suppositions and various model approaches, it is possible with satisfactory for experimental needs exactitude to solve the problem of restoration of the statistics of the roughness and heterogeneities of the refraction index and to determine appropriate parameters of irregularities. If the cross-correlation connections cannot be neglected such simple solution is impossible. However in this case certain model approaches allow to determine for the given specific (or found in another way) correlation function, at least, the parameters of statistical irregularities.
The limited extrapolation of the
restored power spectrum density of roughness ![]() beyond the limits of the range of wave
numbers of the observable scattering substrate-air and substrate modes in the
presence of the given noise has not allowed solving completely the delivered
problem: the error of restoration remained large.
beyond the limits of the range of wave
numbers of the observable scattering substrate-air and substrate modes in the
presence of the given noise has not allowed solving completely the delivered
problem: the error of restoration remained large.
In this connection the procedure of an effective smoothing (quasi-optimal Egorov’s filtration) in the integral Eq. (6) is applied for deriving an approximate correct solution of the inverse waveguide scattering problem [12-14, 18-20, 22-25, 27-29]:
When the spectra of the noise and signal are overlapped this procedure of the filtering permits to achieve more effective elimination of the band-limited “white” additive noise [12-17, 22-25, 27-29] than Wiener filter [15, 16]. In the cases of using of the sampling theorem it is more preferable to restore the autocorrelation function with the use of the quasi-optimum discrete filtration:
where the value n = 0, 1, 2 … N,
m = 0, 1, 2 … M; un = n∙Δu;
βm = m∙Δβ. The
smoothing (filtering) function E(u; γ) is selected
from the condition of the minimum rms error of reconstructing of the specified
ACF ![]() :
:
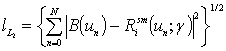 ,
(9)
,
(9)
where the values N, M << ∞.
By applying the Parseval equality to the
Eq. (9), we can consider the obtained expression as the rms error of
approximation of the initial continuous PSD F(β; γ)
![]() L2
(-∞, +∞) with the help of functions (i.e. spectra) of limited
length
L2
(-∞, +∞) with the help of functions (i.e. spectra) of limited
length ![]()
![]() L2 (-β,
+β). The minimum error, accessible for this approximation is equal
to:
L2 (-β,
+β). The minimum error, accessible for this approximation is equal
to:
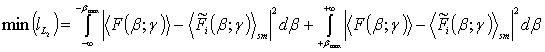 . (10)
. (10)
This error is equal to the “energy” containing mainly in the high-frequency part of the spectrum of the roughness “power” F(β; γ), that is in the range of values │β│> βmax, where βmax determines boundary frequency, after which the optical transfer function of the system is equal to zero. From the viewpoint of the optimum filtration theory formulas Eqs. (7, 8) allows to attenuate mainly high-frequency noise components. Thus, the considered above procedure of searching of the solution of the waveguide inverse problem is reduced to the construction of certain quasi-optimum operator using the least-squares method.
During the modeling on the computer functions M, E, and parameters of the solution of the inverse problem μ, p and γ are varied. The smoothing function has been taken essentially in the simple kind sin(cuβ)/(cuβ) or exp[-a(uβ)2]; c and a can be treated as effective averaging intervals. The obtained outcomes of the computer simulation allow approving that this rather simple procedure allows receiving the approximate correct solution of the waveguide scattering inverse problem with the relative rms error of restoring of an ACF no more than 30% for SNR > 10 [12-14, 18-20, 22-25, 27-29].
We should note that the exactitude of restoring of the experimental ACF achieved by this algorithm is quite sufficient for reliable determination of the subwavelength correlation intervals and rms height of the surface roughness. First we can evaluate from the scattering diagram the experimental ACF of the investigated surface roughness as Gaussian with appropriate geometric parameters σ and r [20]. Then using of our method of reconstruction of the autocorrelation function of the waveguide’s irregularities [12-14, 18-20, 22-25, 27-29] permits to improve this estimation and it is possible to determine the mean parameters of the surface roughness with more accuracy. The determined roughness parameters are in good agreement with the obtained by the SEM and by the standard mechanical profilometer [20]. While the effective filtering and a limited extrapolation are used, the restoring functions became more similar to the initial ones.
The further increase of the exactitude of restoring of the specified ACF (and SDF) and determination of the appropriate parameters of the irregularities is possible, for example, at the expense of the choice of another optimum smoothing functions and the parameters of solution of the problem and also at the expense of application of an effective analytic extrapolation of the spectral density function beyond the limits of the range of registered scattering modes. In this case we should use the following formula for the restoration of the smoothing ACF with the superresolution [12-14, 18-20, 22, 25, 27-29]:
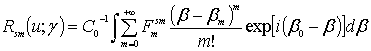 ,
(11)
,
(11)
where ![]() are the smoothed regularized expansion
coefficients. While the experimental data are processed it is necessary to
limit the number m in Eq. (11) due to influences of the calculation errors
and noise.
are the smoothed regularized expansion
coefficients. While the experimental data are processed it is necessary to
limit the number m in Eq. (11) due to influences of the calculation errors
and noise.
Other approaches for finding the correct approximate solution of the delivered problem, especially when reaching the super resolution on lateral sizes of the irregularities are also possible [12-14, 17-30]. It should be noted that a computer realization of all these methods requires first the development of an adequate physical-mathematical model of the waveguide scattering phenomenon. The best results can be obtained if a priori information on the object is known and the noise statistics is determined.
Conclusion
The phenomenon of the waveguide mode scattering in the irregular planar optical waveguide is investigated. The solution of the direct problem is fined with the help of the theory of perturbations. By assuming the absence of the cross-correlation connections between all types of irregularities, it is possible to restore the initial theoretical or experimental autocorrelation function. The solution of the inverse problem is reduced to the restoration of the spectral density function and/or autocorrelation function of the statistic stationary irregularities of the planar optical waveguide by the data of the light scattering in the far zone. This algorithm of solution of the inverse waveguide scattering problem is the combination of the classic regularization and the quasi-optimal filtration (smoothing) of the measured data. To achieve the super resolving in the inverse problem this algorithm must be accomplished at least. Certain extrapolation of the spectral density function of the irregularities beyond the range of the wavenumbers of the registering scattering modes permits to improve the estimations of the restored statistic characteristics and parameters of the irregularities.
The waveguide scattering method in our opinion is the most suited tool for the metrological control in the integrated optics and integrated optoelectronics since the determined characteristics and parameters characterize the waveguide in a whole just as an integrated structure but not as the separated mediums used for its manufacture. And what is more, just these parameters are needed for the final metrological attestation of the integrated optical waveguides.
The waveguide scattering method can be also useful in the biomedical and ecological studies due to its sensitivity to the large changes of the object’s contrast and possibility to obtain statistic information about the ensemble of microobjects in a single measurement over a wide surface area.
REFERENCES
1. Shevchenko V.V. Continuous Transitions in Open Waveguides. Colo.: Golem, Boulder, 1971.
2. Marcuse D. Light Transmission Optics. New York: Van Nostrand, 1972.
3. Walter D.J., Houghton J Attenuation in thin film optical waveguides due to roughness-induced mode coupling // Thin Solid Film. 1978. V. 52. P. 461-476.
4. Bradley E., Hall D.G Out-of-plane scattering from glass waveguides: comparison of theory and experiment // Optics Letters. 1982. V. 7. No. 5. P. 235-237.
5. Gottlieb M., Brandt G.B., Conroy J.J. Out-of-plane scattering in optical waveguides // IEEE Trans. On Circuit and Systems. 1979. V. 26. No. 12. P. 1029-1035.
6. Hall D.G. Scattering of optical guide waves by waveguide surface roughness: a three-dimensional treatment // Optics Letters. 1981. V. 6. No. 12. P. 601-603.
7. Imai M., Koseki M., Ohtsuka Y. Scattering pattern measurement and analysis of sputtered-glass optical waveguides for integrated optics // IEEE Trans. on MTT. 1982. V. 30. P. 635-641.
8. Andler G., Egorov A.A., Cheremiskin I.V. Determination of parameters of a roughness of an optical surface by the scattering in a dielectric waveguide // Optics and Spectroscopy. 1984. V. 56. No. 4. pp. 731-735.
9. Siro F. Vasquez S. de F., Egorov A.A., Cheremiskin I.V. To a problem on determination of statistical characteristics of irregularities of thin-film waveguides // Optoelectronics, Instrumentation and Data Processing. 1991. No. 2. pp. 51-55.
10. Egorov A.A. Characteristics of a radiation, scattered on roughness of a surface substrate of a planar waveguide // Surface. Physics, chemistry, mechanics. 1994. No. 5. pp. 72-76.
11. Egorov A.A. Theory of waveguide optical microscopy // Laser Physics. 1998. V. 8. No. 2. pp. 536-540.
12. Yegorov A.A. Recovery of the characteristics and determination of the parameters of statistical nanometer surface roughness using the data on scattering in a planar optical waveguide // Radiophysics and Quantum Electronics. 2000. V. 43. No. 12. pp. 980-988.
13. Egorov A.A. Using waveguide scattering of laser radiation for determining the autocorrelation function of statistical surface roughness within a wide range of changes of the roughness correlation interval // Quantum Electronics. 2002. V. 32. No. 4. pp. 357-361.
14. Yegorov A.A. A new algorithm of restoring the autocorrelation function of subwavelength statistic surface roughness by light scattering in integrated optical waveguide in the presence of a high additive stochastic noise // Proc. SPIE. 2002. V. 4900. pp. 792-801.
15. Tikhonov A.N., Arsinin V.Y. Solution of ill-posed problem. Washington: Winston/Willey, 1977.
16. Akhmanov S.A., Diakov Yu.E., Chirkin A.S. Introduction to Statistic Radiophysics and Optics. Moscow: Nauka, 1981.
17. Yegorov A.A. Inverse light scattering problem in a planar waveguide with statistical subwavelength irregularities: theory and computer simulation // J. Comput. Methods in Sciences and Engineering. 2002. V. 2. pp. 277-285.
18. Yegorov A.A. Inverse laser irradiation scattering problem in a planar waveguide with statistical irregularities. Computer modeling for a case of large additive “white” noise // Laser Physics. 2003. V. 13. No. 9. pp. 1143-1148.
19. Egorov A.A. Reconstruction of the characteristics and determination of the parameters of a statistical surface roughness from light scattering data in an integrated waveguide in the presence of noise // Optics and Spectroscopy. 2003. V. 95. No. 2. pp. 294-304.
20. Egorov A.A. Reconstruction of the experimental autocorrelation function and determination of the parameters of the statistical roughness of a surface from laser radiation scattering in an integrated-optical waveguide // Quantum Electronics. 2003. V. 33. No. 4. pp. 335-341.
21. Egorov A.A. Theory of laser radiation scattering in integrated optical waveguide with 3D-irregularities in presence of noise: vector consideration // Laser Physics Letters. 2004. V. 1. No. 12. pp. 579-585.
22. Egorov A.A. Inverse problem of laser light scattering in an integrated optical waveguide: 2D solution with accurate input data // Laser Physics. 2004. V. 14. No. 10. pp. 1296-1309.
23. Egorov A.A. Theory of waveguide light scattering in an integrated optical waveguide in the presence of noise // Radiophysics and Quantum Electronics. 2005. V. 48. No. 1. pp. 57-67.
24. Egorov A.A. Use of waveguide light scattering for precision measurements of the statistic parameters of irregularities of integrated optical waveguide materials // Opt. Engineering. 2005. V. 44. No. 1. pp. 014601-1–014601-10.
25. Egorov A.A. Inverse problem of theory of the laser irradiation scattering in two-dimensional irregular integrated optical waveguide in the presence of statistic noise // Laser Physics Letters. 2005. V. 2. No. 2. pp. 77-83.
26. Egorov A.A. 3D Waveguide light scattering. Rigorous and approximate analysis // ICO Topical Meeting on Optoinformatics/Information Photonics 2006. September 4-7 2006. St. Petersburg. Russia. St. Petersburg: ITMO. pp. 371-372.
27. Egorov A.A. Super resolution in the waveguide inverse light scattering problem // Journal of Radio Electronics. 2007. No. 6. pp. 1-9.
28. Egorov A.A. Inverse problem of scattering of monochromatic light in a statistically irregular waveguide: theory and numerical simulation // Optics and Spectroscopy. 2007. V. 103. No. 4. pp. 621-628.
29. Egorov A.A. Theoretical research of correctness of an inverse problem of scattering of laser radiation in a statistically irregular integrated-optical waveguide in the absence of noise // Journal of Radio Electronics. 2009. No. 4. pp. 1-19.
30. Egorov A.A., Sevastianov L.A., Sevastyanov A.L., Stavtsev A.V. Propagation of the monochromatic electromagnetic waves in irregular waveguides. A brief introduction to an analysis in the case of smooth or statistic irregularities // Bulletin of PFUR. Series Mathematics. Computer science. Physics. 2010. No. 1. pp. 67-76.
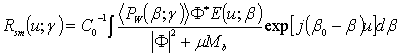 .
(7)
.
(7)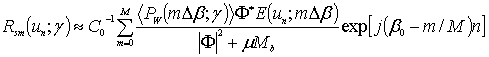 , (8)
, (8)