УДК 621.391.01
ОЦЕНКА МОЩНОСТИ ИНТЕРМОДУЛЯЦИОННЫХ
ПОМЕХ ДЛЯ СИГНАЛОВ С ОРТОГОНАЛЬНЫМ ЧАСТОТНЫМ МУЛЬТИПЛЕКСИРОВАНИЕМ
Л. Е. Назаров¹, А. С. Зудилин²
¹Институт радиотехники и электроники им. В.А.Котельникова РАН, г. Фрязино
²ОАО
“Российские космические системы”, г. Москва
Получена
24 июня 2011 г.
Аннотация. Приведены методики оценки мощности интермодуляционных помех на выходе передатчика как нелинейного устройства для сигналов с частотным ортогональным мультиплексированием, характеризуемых высокими значениями пик/фактор.
Ключевые слова: нелинейности передатчика, OFDM сигналы, интермодуляционные помехи.
Abstract. This paper presents the methods for power evaluation of intermodulation distortions due to nonlinear amplifier for OFDM signals.
Key words: nonlinear power amplifier, OFDM signals, AM/AM and AM/PM characteristics, intermodulation distortion.
Введение
Ансамбли сигналов с ортогональным частотным мультиплексированием известны в литературе как OFDM сигналы (orthogonal frequency-division multiplexing) [1]. Данные сигналы обладают рядом свойств, определяющих перспективность их применения для передачи информации по каналам с многолучевостью. OFDM сигналы являются базовыми для ряда форматов широкополосных систем связи: IEEE 802.16 (WiMax), 3GPP-LTE (Third Generation Partnership Project – Long Term Evolution), IEEE 802.12.11 [1,2].
Одним из недостатков OFDM сигналов является их большое значение параметра пик/фактор. Это приводит к появлению интермодуляционных помех на выходе усилителя мощности передатчика как нелинейного устройства. Актуальной является проблема оценки мощности данных помех. В статье приведены методики оценки мощности рассматриваемых помех, даны результаты расчетов с использованием этих методик для модели передатчика на основе лампы бегущей волны.
1. Постановка задачи
Многочастотные сигналы с ортогональным частотным мультиплексированием представляют сумму ![]() гармонических сигналов, ортогональных на
интервале времени определения (
гармонических сигналов, ортогональных на
интервале времени определения (![]() ) [1]. Спектры составляющих сигналов пересекаются
в общей полосе, поэтому OFDM сигналы
характеризуются большей частотной эффективностью, чем ортогональные сигналы с
частотным разделением, не имеющих пересечения спектров [3].
) [1]. Спектры составляющих сигналов пересекаются
в общей полосе, поэтому OFDM сигналы
характеризуются большей частотной эффективностью, чем ортогональные сигналы с
частотным разделением, не имеющих пересечения спектров [3].
Формирование OFDM сигналов
производится следующим образом. На основе последовательности двоичных кодовых
символов длительностью ![]() , поступающей на
вход модулятора сигналов, формируется
блок длительностью
, поступающей на
вход модулятора сигналов, формируется
блок длительностью ![]() комплексных
дискретных символов {
комплексных
дискретных символов {![]() },
которые определяют комплексную огибающую OFDM сигналов
},
которые определяют комплексную огибающую OFDM сигналов
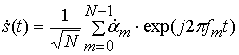 . (1)
. (1)
Объем алфавита символов ![]() равен
равен ![]() . Параметры
. Параметры ![]() связаны соотношением
связаны соотношением ![]() . Ортогональность составляющих
сигналов в (1) на интервале (
. Ортогональность составляющих
сигналов в (1) на интервале (![]() ) обеспечивается выбором
частот
) обеспечивается выбором
частот ![]() для
двумерных сигналов (многофазовая модуляция ФМ-М) или
для
двумерных сигналов (многофазовая модуляция ФМ-М) или ![]() для одномерных сигналов (двухфазовая
модуляции ФМ-2). На вход передатчика поступает вещественный сигнал
для одномерных сигналов (двухфазовая
модуляции ФМ-2). На вход передатчика поступает вещественный сигнал ![]() , здесь
, здесь ![]() - несущая частота.
- несущая частота.
Важным параметром сигналов
является пик/фактор ![]() [3,4],
определяющий динамический диапазон сигналов. Здесь
[3,4],
определяющий динамический диапазон сигналов. Здесь ![]() - средняя мощность сигналов. Для
высоких значений
- средняя мощность сигналов. Для
высоких значений ![]() необходимо
принимать во внимание интермодуляционные помехи, возникающие за счет влияния передатчика
как нелинейного устройства.
необходимо
принимать во внимание интермодуляционные помехи, возникающие за счет влияния передатчика
как нелинейного устройства.
OFDM сигналы
характеризуются высокими значениями пик/фактора - для составляющих сигналов с
постоянной мощностью верно соотношение ![]() [1]. Теоретическое оценивание мощности
интермодуляционных помех OFDM сигналов
составляет суть рассматриваемой задачи.
[1]. Теоретическое оценивание мощности
интермодуляционных помех OFDM сигналов
составляет суть рассматриваемой задачи.
2. Модели нелинейностей
Рассмотрим принятые
в литературе модели нелинейностей передатчика амплитуда/амплитуда (АМ/АМ) и амплитуда/фаза
(АМ/ФМ). Для входного узкополосного сигнала с комплексной амплитудой ![]() комплексная амплитуда
сигнала с выхода передатчика, как нелинейного устройства, может быть записана в
виде [4]
комплексная амплитуда
сигнала с выхода передатчика, как нелинейного устройства, может быть записана в
виде [4]
![]() . (2)
. (2)
Здесь ![]() - нелинейности АМ/АМ и АМ/ФМ.
- нелинейности АМ/АМ и АМ/ФМ.
Для передатчиков на
основе лампы бегущей волны (ЛБВ) модельные нормализованные представления ![]() имеют вид [4]
имеют вид [4]
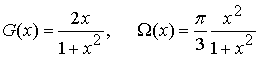 . (3)
. (3)
В точке насыщения при ![]() имеем
имеем ![]() .
.
Известные методы борьбы с нелинейностями основаны на линеаризации каналов, а также на снижении мощности OFDM сигналов на входе передатчика с целью его работы в режиме, близком к линейному режиму.
Суть методов линеаризации
- предварительное искажение сигналов на входе передатчика ![]() с целью компенсации амплитудной и фазовой
нелинейностей. Для этого необходимо, чтобы функции
с целью компенсации амплитудной и фазовой
нелинейностей. Для этого необходимо, чтобы функции ![]() являлись решениями системы
уравнений [4]
являлись решениями системы
уравнений [4]
![]() , (4)
, (4)
![]() . (5)
. (5)
Методы линеаризации
основаны на решениях системы (4), (5) с
использованием приближения ![]() к аппроксимирующей функции
к аппроксимирующей функции ![]() ,
при этом функция
,
при этом функция ![]() соответствует решению уравнения (5) [5]. В
качестве функции
соответствует решению уравнения (5) [5]. В
качестве функции ![]() используется симметричное
ограничение с зоной линейности
используется симметричное
ограничение с зоной линейности
Здесь ![]() - параметр крутизны, при
- параметр крутизны, при ![]() функция
функция ![]() соответствует предельному симметричному ограничителю
без зоны линейности [6].
соответствует предельному симметричному ограничителю
без зоны линейности [6].
Влияние линеаризованного
канала (6) на OFDM сигналы ![]() тождественно ограничению их амплитуд,
что приводит к возникновению интермодуляционных помех [6]. Ниже
приведены методики оценки общей мощности этих помех, а также их мощности в полосе OFDM сигналов с модуляцией ФМ-4.
тождественно ограничению их амплитуд,
что приводит к возникновению интермодуляционных помех [6]. Ниже
приведены методики оценки общей мощности этих помех, а также их мощности в полосе OFDM сигналов с модуляцией ФМ-4.
3. Методики оценки общей мощности интермодуляционных помех
Методика оценки общей
мощности интермодуляционных помех для нелинейного элемента ![]() основана на корреляционной связи входных OFDM сигналов
основана на корреляционной связи входных OFDM сигналов ![]() , как гауссовского процесса (при
условии
, как гауссовского процесса (при
условии ![]() [7]) с
нулевым средним и дисперсией
[7]) с
нулевым средним и дисперсией ![]() , и выходного процесса
, и выходного процесса ![]() [8]
[8]
![]() . (7)
. (7)
Здесь ![]() - взаимная корреляционная функция
- взаимная корреляционная функция ![]() и
и ![]() ;
; 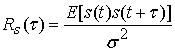 - нормированная корреляционная функция OFDM сигналов;
- нормированная корреляционная функция OFDM сигналов; 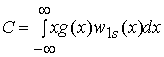 ;
; 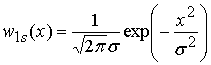 - одномерная плотность распределения
- одномерная плотность распределения ![]() . Таким образом,
мощность полезного сигнала в
. Таким образом,
мощность полезного сигнала в ![]() равна
равна ![]() , мощность
, мощность ![]() и полная мощность интермодуляционных помех
равны
и полная мощность интермодуляционных помех
равны 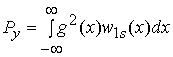 и
и ![]() .
.
Для неинерционного
нелинейного элемента ![]() в виде симметричного ограничителя с зоной линейности (6) мощность полезного сигнала
в виде симметричного ограничителя с зоной линейности (6) мощность полезного сигнала ![]() и мощность процесса
и мощность процесса ![]() определяются соотношениями
определяются соотношениями
Здесь 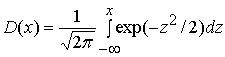 - интеграл ошибок.
- интеграл ошибок.
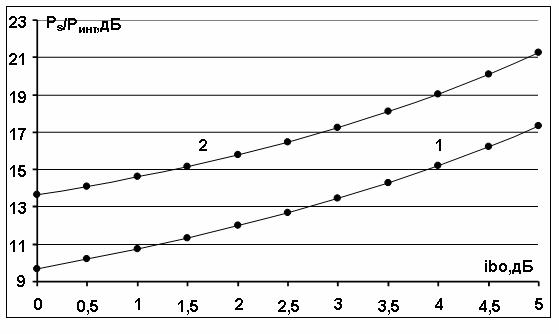
Рис.1. Зависимость отношения сигнал/помеха на выходе ограничителя с зоной линейности от снижения мощности OFDM сигналов ![]() на
на ![]() на входе передатчика: 1
– общая мощность интермодуляционных помех; 2 –
мощность интермодуляционных помех в полосе OFDM сигналов.
на входе передатчика: 1
– общая мощность интермодуляционных помех; 2 –
мощность интермодуляционных помех в полосе OFDM сигналов.
На рис.1 приведена зависимость
(кривая 1) сигнал/помеха 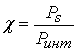 от снижения
мощности
от снижения
мощности ![]() входных
OFDM сигналов на
входных
OFDM сигналов на ![]() (дБ) по отношению к исходной мощности,
равной 1. Кривая рассчитана с использованием соотношений (8), (9) для
(дБ) по отношению к исходной мощности,
равной 1. Кривая рассчитана с использованием соотношений (8), (9) для ![]() . При
. При ![]() дБ вероятность превышения
амплитуды сигналов единичного уровня равна 0.31 и отношение сигнал/помеха равно
дБ вероятность превышения
амплитуды сигналов единичного уровня равна 0.31 и отношение сигнал/помеха равно
![]() дБ. При уменьшении мощности сигналов
в 2 раза (
дБ. При уменьшении мощности сигналов
в 2 раза (![]() дБ) вероятность превышения амплитуды
сигналов единичного уровня равна 0.16 и отношение сигнал/помеха увеличивается и
равно
дБ) вероятность превышения амплитуды
сигналов единичного уровня равна 0.16 и отношение сигнал/помеха увеличивается и
равно ![]() дБ.
дБ.
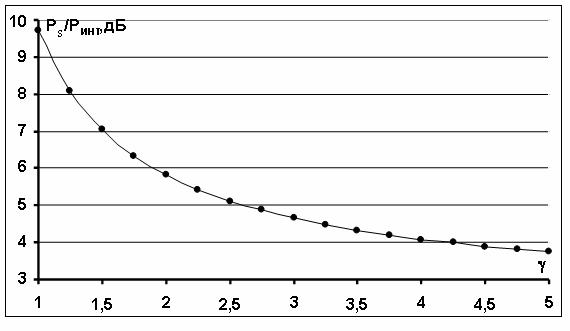
Рис.2. Кривая зависимости сигнал/помеха ![]() на выходе симметричного ограничителя
на выходе симметричного ограничителя
с зоной линейности от значений коэффициента крутизны ![]() .
.
На рис.2 приведена кривая
зависимости сигнал/помеха ![]() от значений коэффициента
от значений коэффициента ![]() .
Кривая рассчитана с использованием соотношений (8), (9) для OFDM сигналов с мощностью
.
Кривая рассчитана с использованием соотношений (8), (9) для OFDM сигналов с мощностью ![]() . При увеличении
. При увеличении ![]() значения
значения ![]() уменьшаются, приближаясь к минимальному предельному значению
уменьшаются, приближаясь к минимальному предельному значению ![]() .
.
Для коэффициента ![]() функция нелинейности
функция нелинейности ![]() (6) соответствует предельному симметричному ограничителю
без зоны линейности, при этом имеем
(6) соответствует предельному симметричному ограничителю
без зоны линейности, при этом имеем ![]() ,
, ![]() и отношение сигнал/помеха равно
и отношение сигнал/помеха равно ![]() (2.45 дБ). Это
значение получено предельным переходом в (8), (9) с использованием приближения
(2.45 дБ). Это
значение получено предельным переходом в (8), (9) с использованием приближения ![]() для
для ![]() . Результаты
компьютерного моделирования для OFDM
сигналов, содержащих
. Результаты
компьютерного моделирования для OFDM
сигналов, содержащих ![]() составляющих
сигналов с ФМ-4 модуляцией, подтвердили приведенное значение
составляющих
сигналов с ФМ-4 модуляцией, подтвердили приведенное значение ![]() . Для ФМ-4 модуляции верным
является соотношение
. Для ФМ-4 модуляции верным
является соотношение 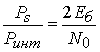 ,
где
,
где ![]() - энергия
сигналов на информационный бит,
- энергия
сигналов на информационный бит, ![]() - односторонняя спектральная плотность мощности помех. Для соответствующего
значения
- односторонняя спектральная плотность мощности помех. Для соответствующего
значения 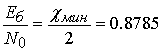 (-0.56 дБ) вероятность
ошибки на бит при приеме OFDM сигналов
без кодирования равна
(-0.56 дБ) вероятность
ошибки на бит при приеме OFDM сигналов
без кодирования равна ![]() .
Это совпадает со значением
.
Это совпадает со значением ![]() , полученным авторами путем моделирования.
, полученным авторами путем моделирования.
4. Оценка мощности интермодуляционных помех в полосе OFDM сигналов
Рассмотрим OFDM сигналы с несущей частотой ![]() , полосой
, полосой ![]() , мощностью
, мощностью ![]() и нормированной корреляционной функцией
и нормированной корреляционной функцией
![]() . Двусторонний нормированный спектр мощности
. Двусторонний нормированный спектр мощности
![]() сигналов
можно рассматривать как прямоугольный
сигналов
можно рассматривать как прямоугольный ![]() при
при ![]() , иначе
, иначе ![]() , и относительно корреляционной
функции в области видеочастот
, и относительно корреляционной
функции в области видеочастот ![]() справедливо
соотношение
справедливо
соотношение ![]() [7].
[7].
Анализ интермодуляционных
помех в полосе ![]() сначала
проведем для предельного симметричного
ограничителя без зоны линейности. В этом случае функция корреляции
сначала
проведем для предельного симметричного
ограничителя без зоны линейности. В этом случае функция корреляции ![]() имеет вид [8,9]
имеет вид [8,9]
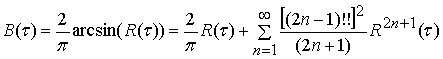 . (10)
. (10)
Здесь ![]() - произведение нечетных положительных
целых чисел до (
- произведение нечетных положительных
целых чисел до (![]() )
включительно.
)
включительно.
Член ![]() (10) соответствует полезному
сигналу с мощностью
(10) соответствует полезному
сигналу с мощностью ![]() и спектральной
плотностью
и спектральной
плотностью ![]() .
.
В полосу OFDM сигналов попадают интермодуляционные
помехи, соответствующие членам суммы (10) с множителем ![]() . Корреляционная функция
. Корреляционная функция ![]() для данных помех имеет вид
[8]
для данных помех имеет вид
[8]
Здесь 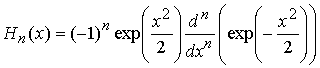 - полиномы Эрмита; для рассматриваемой
нелинейности
- полиномы Эрмита; для рассматриваемой
нелинейности ![]() справедливо соотношение
справедливо соотношение
![]() [9].
[9].
Выражение для оценки
минимального количества ![]() членов в ряде Тейлора (11),
обусловливающее абсолютную погрешность
членов в ряде Тейлора (11),
обусловливающее абсолютную погрешность ![]() при вычислении функции корреляции
при вычислении функции корреляции ![]() , имеет вид
, имеет вид
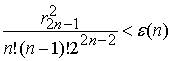 . (13)
. (13)
В соответствии с теоремой
Хинчина-Винера спектральная плотность интермодуляционных помех ![]() в полосе OFDM сигналов может быть определена путем
преобразования Фурье функции
в полосе OFDM сигналов может быть определена путем
преобразования Фурье функции ![]() (11) [8]. При этом спектральная плотность
(11) [8]. При этом спектральная плотность ![]() , соответствующая корреляционной
функции
, соответствующая корреляционной
функции ![]() ,
может быть вычислена с использованием свертки
,
может быть вычислена с использованием свертки 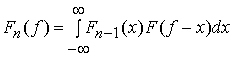 . Этот подход позволяет оценить спектральную
плотность интермодуляционных помех
. Этот подход позволяет оценить спектральную
плотность интермодуляционных помех ![]() в полосе OFDM сигналов и оценить зависимость значений сигнал/помеха
в полосе OFDM сигналов и оценить зависимость значений сигнал/помеха 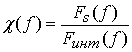 от частоты
от частоты ![]() .
.
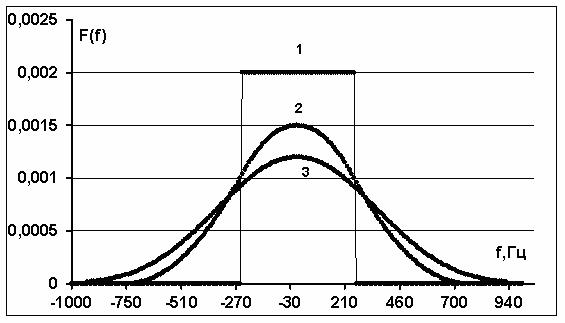
Рис. 3. Кривая 1 – спектральная плотность OFDM сигналов, соответствующая корреляционной функции ![]() (
(![]() Гц); кривая 2 – спектральная плотность
интермодуляционных помех, соответствующая
Гц); кривая 2 – спектральная плотность
интермодуляционных помех, соответствующая ![]() ; кривая 3 – спектральная плотность интермодуляционных
помех, соответствующая
; кривая 3 – спектральная плотность интермодуляционных
помех, соответствующая ![]() .
.
На рис. 3 в
качестве примера приведена кривая 1 исходного спектра OFDM сигналов в области
видеочастот, соответствующего корреляционной функции ![]() для значения
для значения ![]() Гц, а также кривые для спектров
интермодуляционных помех, соответствующих корреляционным функциям
Гц, а также кривые для спектров
интермодуляционных помех, соответствующих корреляционным функциям ![]() (кривая 2) и
(кривая 2) и ![]() (кривая 3).
(кривая 3).
Рис.4. Зависимость сигнал/помеха 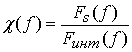 от частоты в полосе OFDM сигналов: 1 - предельный ограничитель без зоны линейности; 2 - предельный
ограничитель с зоной линейности.
от частоты в полосе OFDM сигналов: 1 - предельный ограничитель без зоны линейности; 2 - предельный
ограничитель с зоной линейности.
На рис.4 (кривая 1) приведена
зависимость ![]() ,
вычисленная с использованием данной методики для рассматриваемого ансамбля OFDM сигналов с полосой
,
вычисленная с использованием данной методики для рассматриваемого ансамбля OFDM сигналов с полосой ![]() Гц. Вычисление произведено с использованием
Гц. Вычисление произведено с использованием ![]() членов в (11), что соответствует
точности оценки
членов в (11), что соответствует
точности оценки ![]() не
хуже
не
хуже ![]() =0.001.
Видна неравномерность распределения мощности интермодуляционных помех в полосе OFDM сигналов - различие значений в центре
=0.001.
Видна неравномерность распределения мощности интермодуляционных помех в полосе OFDM сигналов - различие значений в центре
![]() дБ и по краям
полосы
дБ и по краям
полосы ![]() дБ равно
1.37 дБ. Значение
дБ равно
1.37 дБ. Значение ![]() дБ
в центре полосы совпадает со значением, приведенным в [4]. Кривая 1 на рис.4 согласуется с
результатами моделирования, приведенными в работе [10], где показано повышение
сигнал/помеха на краях полосы (
дБ
в центре полосы совпадает со значением, приведенным в [4]. Кривая 1 на рис.4 согласуется с
результатами моделирования, приведенными в работе [10], где показано повышение
сигнал/помеха на краях полосы (![]() дБ) и понижение в центре полосы сигналов (
дБ) и понижение в центре полосы сигналов (![]() дБ). Наблюдаемое различие
оценок моделирования
дБ). Наблюдаемое различие
оценок моделирования ![]() по отношению к теоретическим оценкам объясняется
несовершенством используемой методики моделирования [10], не учитывающей вклада
продуктов нелинейности анализируемого составляющего сигнала в мощность
интермодуляционных помех.
по отношению к теоретическим оценкам объясняется
несовершенством используемой методики моделирования [10], не учитывающей вклада
продуктов нелинейности анализируемого составляющего сигнала в мощность
интермодуляционных помех.
Оценим мощность интермодуляционных
помех в полосе ![]() для
симметричного
ограничителя с зоной линейности
для
симметричного
ограничителя с зоной линейности ![]() (6) (
(6) (![]() ). В этом случае сигнальная составляющая на
выходе соответствует величине
). В этом случае сигнальная составляющая на
выходе соответствует величине ![]() , задаваемой интегральным соотношением
(12). Результирующее выражение для мощности полезных сигналов
, задаваемой интегральным соотношением
(12). Результирующее выражение для мощности полезных сигналов ![]() после выполнения
интегрирования (12) имеет вид
после выполнения
интегрирования (12) имеет вид 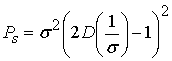 и совпадает с выражением (8).
и совпадает с выражением (8).
Корреляционная функция ![]() для данных помех в
полосе OFDM сигналов определяется соотношением (11), соответствующее выражение
для множителя
для данных помех в
полосе OFDM сигналов определяется соотношением (11), соответствующее выражение
для множителя ![]() после выполнения интегрирования (12) имеет вид
после выполнения интегрирования (12) имеет вид 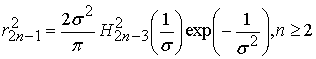 [9].
[9].
На рис.1 (кривая 2) приведена
зависимость усредненных значений сигнал/помеха 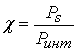 (дБ) от снижения
мощности
(дБ) от снижения
мощности ![]() входных
OFDM сигналов на
входных
OFDM сигналов на ![]() (дБ) по отношению к исходной мощности,
равной 1. Эта кривая рассчитана с использованием соотношений (11), (12). При
(дБ) по отношению к исходной мощности,
равной 1. Эта кривая рассчитана с использованием соотношений (11), (12). При ![]() дБ отношение
дБ отношение ![]() равно
равно ![]() дБ. При уменьшении
мощности сигналов отношение сигнал/помеха
увеличивается и для значения
дБ. При уменьшении
мощности сигналов отношение сигнал/помеха
увеличивается и для значения ![]() дБ (уменьшение
мощности сигналов в 2 раза) отношение
дБ (уменьшение
мощности сигналов в 2 раза) отношение ![]() равно
равно ![]() дБ. Видно также, что общая мощность
интермодуляционных помех превышает мощность данных помех в полосе OFDM сигналов на 4 дБ.
дБ. Видно также, что общая мощность
интермодуляционных помех превышает мощность данных помех в полосе OFDM сигналов на 4 дБ.
На рис.4 (кривая 2) приведена
зависимость сигнал/помеха ![]() . Кривая соответствует значению
. Кривая соответствует значению ![]() дБ. Видна неравномерность распределения
мощности интермодуляционных помех в полосе OFDM сигналов - различие в центре
дБ. Видна неравномерность распределения
мощности интермодуляционных помех в полосе OFDM сигналов - различие в центре ![]() дБ и по краям полосы
дБ и по краям полосы ![]() дБ равно 1.73 дБ.
дБ равно 1.73 дБ.
Заключение
Приведены методики оценивания общей мощности интермодуляционных помех для OFDM сигналов и мощности этих помех в полосе сигналов на выходе передатчика как нелинейного устройства. Основу данных методик составляют методы теории нелинейных преобразований гауссовских случайных процессов. С использованием этих методик произведены оценки мощностей интермодуляционных помех для ансамблей OFDM сигналов с числом составляющих сигналов, превышающим 250 (при этом сигналы можно рассматривать как гауссовский процесс). Показано, что для данных помех характерна неравномерность распределения их мощности в полосе OFDM сигналов - различие значений в центре и по краям полосы достигает 1.7 дБ для модели нелинейности в виде ограничителя с зоной линейности. Это обусловливает необходимость разработки соответствующих процедур обработки OFDM сигналов при их приеме с учетом моделей помех, учитывающих данное свойство неравномерности их спектра.
Литература
1. Hara S., Prasad R. Multicarrier Techniques for 4G Mobile Communications. Artech House. Boston. 2003.
2. Liu H., Li G. OFDM-Based Broadband Wireless Networks. A John Wiley & Sons. New Jersey. 2005.
3. Тепляков И.М., Рощин Б.В., Фомин А.И., Вейцель В.А. Радиосистемы передачи информации. М.: Радио и связь. 1982.
4. Saleh A.A.M., Salz J. Adaptive Linearization of Power Amplifiers in Digital Radio Systems.// The Bell System Technical Journal. 1983. Vol.62. N4. P.1019-1033.
5. Benedetto M-G.D., Mandarini P. An Application of MMSE Predistortion to OFDM Systems.// IEEE Transactions on Communications. 1996. Vol.44. N11. P.1417-1420.
6. Спилкер Дж. Цифровая спутниковая связь. Пер. с англ. М.:Связь. 1979.
7. Гоноровский И.С. Радиотехнические цепи и сигналы. М.: Радио и связь. 1986.
8. Левин Б.Р. Теоретические основы статистической радиотехники. Книга первая. М.:Сов. радио. 1969.
9. Миддлтон Д. Введение в статистическую теорию связи. Пер. с англ. М.: Сов. радио. 1961.
10. Назаров Л.Е., Зудилин А.С. Влияние нелинейностей передатчика на многочастотные сигналы с ортогональным частотным мультиплексированием. //Журнал радиоэлектроники (электронный журнал). http://jre.cplire.ru/jre/dec10/index.html. 2010. №12. Декабрь.
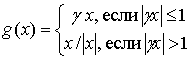 . (6)
. (6)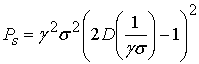
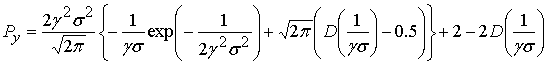 . (9)
. (9)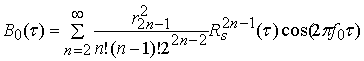 . (11)
. (11)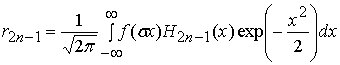 . (12)
. (12)