Обнаружение замираний Райса и Релея в спутниковых радиосигналах на фоне гауссовского шума

ОБНАРУЖЕНИЕ ЗАМИРАНИЙ РАЙСА И РЕЛЕЯ В СПУТНИКОВЫХ РАДИОСИГНАЛАХ НА ФОНЕ ГАУССОВCКОГО ШУМА

А. Эспиноса Мильан, В. М. Шахпаронов

Московский Государствениый Университет Имени М. В. Ломоносова,
физический факультет

Получена 29 июня 2011 г.

Аннотация. В данной работе предлагается методика для обнаружения замираний Райса и Релея в спутниковых радиосигналах на фоне гауссовcкого шума с помощью биспектрального анализа. Предлагаемая методика основана на обнаружении нелинейных признаков, возникающих вследствие интерфирирующих лучей, составляющих приемный сигнал. В работе были использованы тест на нелинейность и тест на гауссовость, основанные на изучении нелинейных компонент бикогерентности сигнала, также была использована сумма нелинейных компонент в качестве показателя степени нелинейности и интенсивности замираний.

Ключевые слова: замирания Райса, замирания Релея, биспектр, бикогерентность, нелинейность.

Abstract. This paper proposes a method for Rice and Rayleigh fading detection in satellite radio signals using bispectral analysis. The proposed methodology is based on the detection of non-linear features that appear due the interfering rays that form the received signal. Nonlinearity test and Gaussian test used in this analysis are based on the study of nonlinear components of signal bicoherence. The sum of non-linear component of the bicoherence was used as an indicator of the degree of nonlinearity and the intensity of fading.

Keywords: Rician fading, Rayleigh fading, bispectrum, bicoherence, nonlinearity.

Введение
Ионосфера является плазменной оболочкой Земли. Ее состав и поведение претерпевают постоянные изменения в зависимости от различных факторов. Одним из таких изменений является возникновение неоднородностей, заключающихся в появлении различной плотности плазмы в слоях ионосферы. Это явление обусловливает появление фазовых и амплитудных флуктуаций, нелинейных искажений и т.д. Такие флуктуации известны в научной литературе как замирания.

Замирания Релея и Райса являются результатом интенсивных нелинейных процессов, возникающих при взаимодействии радиосиналов с изменением концентрации заряженных частиц в плазме ионосферы. Вследствие этих процессов возникает большое количество интерферирующих лучей в приемной антенне наземного комплекса управления спутника. Это явление можно изучать с помощью статистических моделей замираний Релея и Райса, однако, если кроме замираний присутствует высокий уровень гауссовского шума, то результаты не всегда ясны.

Большое количество авторов предлагают методы идентификации стационарных сигналов на фоне мультипликативного шума (в том числе замираний) в разных научных и технических областях, например, в телекоммуникационных системах, в физике плазмы, в механических колебаниях и т.д. [1-3]. Но для данного анализа необходимо не идентифицировать стационарные сигналы, а обнаружить присутствие замираний как признак нелинейного процесса. Таким образом задача состоит в том, чтобы оценить нелинейные признаки в спутниковых радиосигналах. Оценка нелинейности во временных рядах расмотренна в разных работах с разными методиками, например, суррогаты данных [4], статистический анализ [5], вейвлет анализ [6], статистика высокого порядка [7], и т.д. Но одним из наиболее используемых методов является биспектральный анализ.

Первыми авторами, использовавшими биспектр для создания теста на нелинейность, были Субба Рао и Габр [8], но они не обратили внимания на асимптотические свойства биспектра. Хинич [9] создал тест на гауссовость и тест на нелинейность на основе нормализированого биспектра. Тест состоит в том, что квадрат бикогерентности равен нулю, если временые ряды имеют нормальную функцию распределения вероятности. Если же временные ряды являются не гауссовскими, но линейными, то квадрат бикогерентности имеет постоянное значение. Поскольку временные ряды ограничены по времени и имеют узкополосную частоту, невозможно определить настоящий биспектр, можно только получить эстиматор биспектра. Для того, чтобы получить хороший эстиматор биспектра, необходимо применить разные методы для смягчения биспектра в домене времени (например, умножение данных на определенную функцию окна) или в домене частоты (например, фильтрации).

В данной работе представлена методика для обнаружения замираний Релея и Райса с помощью анализа нелинейности спутниковых радиосигналов на основе биспектрального анализа. Также представлены результаты применения предлагаемого метода анализа при анализе ряда сигналов с различной степенью замирания.

Замирания в спутниковых сигналах

Нелинейные флуктуации амплитуды радиосигналов, проходящие через неоднородности в ионосфере, обычно имеют случайный характер. Для анализа замираний в радиосигналах изучается амплитуда квадратурных компонент возникающая вследствие интерференции сигналов с одинаковой чистотой, но с разными фазами, и его фунция распределения. Замирания, присутствующие в спутниковых радиосигналах, обычно делится на два типа: медленные замирания и быстрые замирания. Медленные замирания характеризуется их "моделью", где амплитудное распределение будет логарифмически-нормальным, если амплитуда измеряется единицами Ватт. Если же амплитуда измеряется в децибелах, то распределение будет нормальным. Логарифмически-нормальным распределение определяется следующим уравнением:

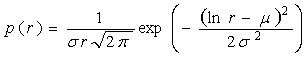, (1)

где - это среднее значение и - это стандартное отклонение .

Быстрые замирания появляются, когда на несущий сигнал влияют другие сигналы одинаковой частоты. Если уровень замираний в канале связи высокий, т.е. количество квадратурнных компонент очень большое, и ни одна из компонент не превышает по амплитуде все остальные, то амплитудное распределение сигнала становится распределением Релея. Распределение Релея определяется следующим образом:

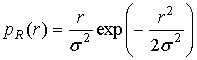, (2)

где является амплитудой огибающей принимаемого сигнала и - средней энергией сигнала. Когда в принятом сигнале существует доминантная квадратурнная компонента, амплитудное распределение становится распределением Райса.

Степень замираний определяется коэффициентом K от функции распределения Райса. Если K стремится к бесконечности, замирания будут минимальными, если K стремится к нулю или равно нулю, замирания будут полными, а амплитудное распределение становится распределением Релея. Распределение Райса определяется следующей формой:

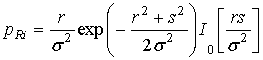, (3)

где - это модифицированная функция Бесселя и - это амплитуда постоянной составляющей сигнала.

K определяется таким образом:

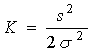(4)

На спутниковые системы коммуникации оказывает большое влияние ионосфера в связи с плотностью электронов и ее изменениями, которые приводят к высокой степени замирания Райса или Релея в спутниковых радиосигналах. Отношение сигнал-шум (S/N) испытывают замирания в зависимости от изменений в плотности электронов. Данное замирание зависит от частоты сигнала и может достигать 30 децибелов.

Методика

Биспектральный анализ обладает рядом особых преимуществ, позволяющих ему превзойти обычный спектральный анализ. Первое и главное преимущество – это возможность удаления гауссовских сигналов (гауссовского шума) при вычислении биспектра сигнала. Второе преимущество – это возможность наблюдения разницы фазы между некоторыми сигналами. Третье преимущество – возможность обнаружения квадратурнных фазовых связей. Однако существует одна проблема: если сигнал ограничен во времени, то в биспектре сигнала появляются соответствующие компоненты. Поэтому необходимо обеспечить сглаживание биспектра, используя функцию «окна», как в случае обычного спектрального анализа.

Для получения биспектра выполняется преобразование Фурье третьего кумулянта сигнала, как это показано в уравнении 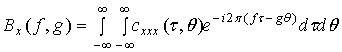(5):

(5)

Бикогерентность является квадратом нормированного биспектра, то есть:

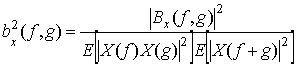(6)

Биспектр находится в зависимости от двух частот f и g. Следовательно, при вычислении биспектра или бикогерентности появляется возможность наблюдать фазу сигналов, т.е. все отношении (f,g,f+g) [9].

Хинич предложил несколько работ [9-11], в которых посредством анализа регионов биспектра ряда данных возможно обнаружить краткосрочные сигналы, негауссовские сигналы и установить нелинейное взаимодействие между несколькими сигналами. В соответствии с теорией Хинича, возможно установить определенные характеристики биспектра для стационарных сигналов и нелинейных процессов.

Хинич установил следующие характеристики для непрерывного биспектра [9]:

Домен непрерывного биспектра является:

Домен прерывного биспектра является:

Область биспектра для стационарнного сигнала является: .

Область, в которой биспектр должен быть равен нулю для стационарной функции, находится в пределах следующего треугольника:

Следовательно, если сигнал является нестационарным, в области присутствуют компоненты с большими значенями. Хинич в этом случае предлагает тест для обнаружения нестационарных сигналов на основе анализа области [9].

Существует одна проблема в использовании биспектра при создании тестов на нелинейность. Амплитуда биспектра не имеет точных пределов, вследствие чего анализ на сравнение разных временых рядов сильно затрудняется. Поэтому ряд авторов предпочитает использовать бикогерентность вместо биспектра, поскольку бикогерентность находится в пределах между нулем и единицей [9]. Основание анализа бикогерентности состоит в том, что является постоянной величиной для линейных функций.

Хинич [9] доказал, что для эстиматора бикогерентности, квадратом бикогерентности на каждой частоте является функция хи-квадрат с двумя степенями свободы для гауссовских функций, и создал один тест на гауссовость и один тест на нелинейность на базе этого основания, однако аккумулятивная ошибка в его тесте может достигать большого значения. Другие авторы предлагают тесты для идентификации нелинейности на базе теории Хинча. В частности, Чудхури и др. [12] предлагает следуюший статистический тест:

(7)

где – это количество сегментов, с помощью которых подсчитывается бикогерентности, и - это критическое значение, рассчитанное исходя из распределения хи-квадрат с двумя степенями свободы для определенного значения .

Из уравнения (7) Чудхури сформулировал два теста. Первый из них, тест на гауссовость, основывается на следующем индексе [12]:

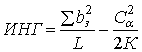(8)

где являются значениями квадрата бикогерентности, отвечающими формуле (7), и является числом компонентов . Можно понять, что для гауссовских рядов результат данного гауссовского показателя будет отрицательным, либо равен нулю, в то время как для негауссовских рядов его результат будет больше нуля.

Также если сигнал не гауссовский, то Чудхури предлагает следующий тест на нелинейность [12]:

, (9)

где и являются средним значением и стандартным отклонением надежных компонент бикогерентности, которые можно получить посредством надежной статистики. Автор предлагает исключить 10% максимальных и 10% минимальных компонент по магнитуде. - это максимальное значение эстиматора квадрата бикогерентности.

Большинство тестов на нелинейность не является показателем степени нелинейности в изученных системах. Некоторые авторы решают этот вопрос, рассчитывая количество нелинейных компонент в биспектре или в бикогерентности [13,14].

Анализ замираний сложно осуществить, если в сигналах, кроме замираний, присутствует влияние гауссовского шума или помехи. Если отношение сигнал-шум в радиосигналах очень низкое, то замирания в этом случае трудно обнаружить через спектральный анализ, поэтому в данной работе было принято решение использовать примущества биспектрального анализа посредством теста на нелинейность на основе уравнений (8) и (9). В следующем разделе представлены результаты тестов на гауссовость и на нелинейность симулированных сигналов с замираниями Райса со значением показателя K от 0 до 6, и с отношением сигнал/шум от 3 дб до 10 дб. Также определяются пределы, для которых работает данная методика и обсуждается ее примущество при обнаружении неоднородностей и при определении степени неоднородности.

Результаты и обсуждение

Перед тем как получить результаты симулированных сигналов с замираниями Райса, сначала надо определить пределы, для которых будут описаны результаты теста на гауссовость. На рисунке 1 представлены результаты теста на гауссовость ста гауссовских временых рядов, каждый из которых имел тысячу отчетов. На рисунке видно, что индекс гауссовости меняется премерно в пределах от 1.1 х до 1.3 х , среднее значение реализации будет равно 1.2 х и стандартное отклонение равно 5.56 х . Таким образом, для данной задачи сигнал будет считаться гауссовским, если результаты теста находятся в пределах между значенями 1.09 х и 1.31 х .

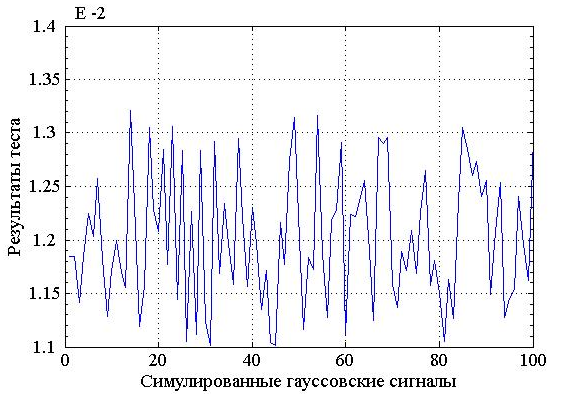
Рисунок 1. Результаты теста на гауссовость ста гауссовских временых рядов, каждый из которых имеет тысячу отчетов.

На рисунках 2 и 3 представлены результаты тестов на гауссовость и на нелинейность симуляции сигналов с разной степенью замирания Райса со значением от нуля до шести показателя К и с разными значениями отношения сигнал/шум. Симуляция была сделана с временными рядами, каждый из которых имеет 1000 отчетов. Можно сформулировать одно важное замечание, рассматривая эти рисунки: методика работает только для сильных замираний, т.е. работает при К < 0.5. Для замираний Райса с К >0.6 результат теста на гауссовость не превышает значение 1.3 х , поэтому эти замирания в данной методике могут быть перепутаны с гауссовским шумом.

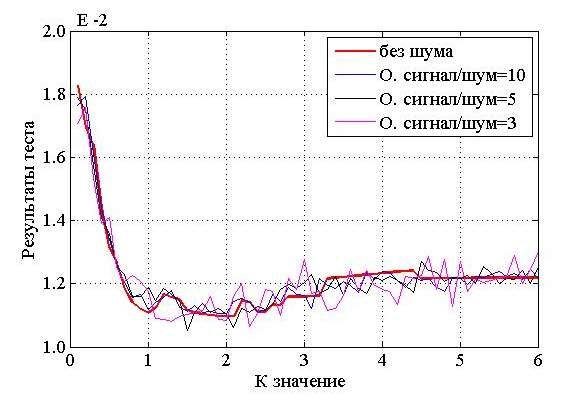
Рисунок 2. Результаты теста на гауссовость для сигналов с замираниями с разными значениями К показателя (от 0 до 6) и с отношением сигнал/шум 10 ДБ, 5ДБ и 3 ДБ.

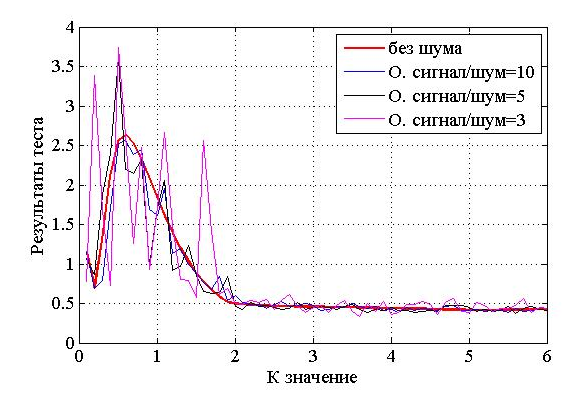
Рисунок 3. Результаты теста на нелинейность для сигналов с замираниями с разными значениями показателя K (от 0 до 6) и с отношением сигнал/шум 10 ДБ, 5ДБ и 3 ДБ.

На рисунке 3 представлены результаты теста на нелинейность, которые позволяют обнаружить замирания в спутниковых сигналах даже при К>6, но результаты теста на гауссовость ограничивают возможность обнаружить замирания Райса с К>0.5. Результаты теста на нелинейность идентифицируют замирания, но не позволяют рассчитать степень нелинейности при разных значениях отношения сигнал/шум. Для вычисления степени нелинейности было решено использовать сумму компонент, которые не выполняют уравнение (7). Т.е. нелинейности бикогерентности, которые появляются из-за квадратурных компонент приемного сигнала на наземной станции спутника.

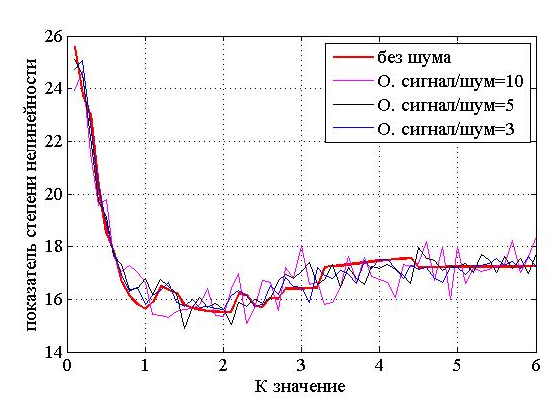
Рисунок 4. Результаты суммы нелинейных компонент для сигналов с замираниями с разными значениями показателя К (от 0 до 6) и с отношением сигнал/шум 10 ДБ, 5ДБ и 3 ДБ.

На рисунке 4 представлены результаты суммы нелинейности бикогеретности. Очевидно, что ошибка в расчете суммы нелинейности бикогерентности зависит от отношения сигнал/шум. При большом значении ошибки невозможно рассчитать интенсивность замираний посредством суммы нелинейности бикогерентности. На рисунке 5 представлено отношение между ошибкой в расчете суммы и отношением сигнал/шум. Для того, чтобы сигнал с замираниями невозможно было перепутать с белым гауссовским шумом, ошибка должна быть меньше 0.73%. Это условие выполняется только при отношении сигнал/шум больше или равно 3 ДБ.

После анализа ошибки в расчете суммы нелинейности относительная от отношении сигнал/шум, можно определить полные пределы, в которых анализ спутниковых радиосигналов будет работать. Количество отчетов временных рядов, описывающих радиосигнал, будет равен 1000. Минимальный коэффицент К замираний, который можно обнаружить, будет равен 0.5, но интенсивность замираний, которую можно рассчитать с помощью данного анализа, будет ниже 0.4 при отношении сигнал/шум > 3 ДБ. Метод имеет силу для замираний Релея, если K=0.

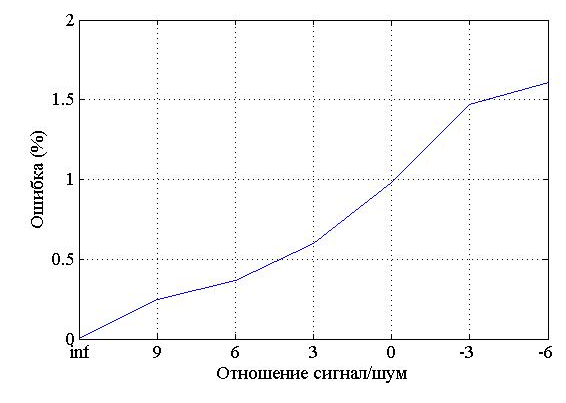
Рисунок 5. Связь между ошибкой в сумме нелинейности бикогерентности и отношением сигнал/шум.

Полученные результаты доказывают, что возможно идентифицировать наличие сильных замираний Райса или Релея и установить степень замирания, даже если амплитудное распределение не будет отвечать ни одному из этих распределений. Как известно, основным источником этих видов замираний является наличие неоднородностей в слоях плазмы в ионосфере. Следовательно, с помощью изучения нелинейностей также можно сделать выводы о характеристиках плазменных процессов в момент распространения спутниковых сигналов.

Выводы

В данной работе была предложена новая форма обнаружения замираний Райса и Релея в спутниковых сигналах посредством биспектрального анализа. Предложенный метод основывается на применении тестов на гауссовость и на нелинейность, основанных на изучении нелинейности бикогерентности анализируемых сигналов. Кроме того, предлагается вычисление суммы нелинейных компонент бикогерентности в качестве показателя нелинейности сигнала.

Поскольку используемая модель нахождения замираний в спутниковых сигналах является моделью замираний Райса, возможно установить отношение между вычислением нелинейности и степенью замираний Райса благодаря количеству существующих квадратурных компонент, даже если амплитудное распределение сигнала не будет в точности отвечать распределению Райса или Релея. В связи с тем, что основные источники замираний в спутниковых сигналах являются ионосферными неоднородностями, результаты, полученные в данной работе, могут быть применены для получения показателя характеристик упомянутых неоднородностей. В будущих работах этот метод будет применен для анализа настоящих спутниковых сигналов и сравнения результатов с ионосферными явлениями, вызывающими неоднородности, такими как солнечная активность и геомагнитная активности Земли.

Литература

1. O. Besson, F. CastanieH, On estimating the frequency of a sinusoid in autoregressive multiplicative noise. Signal Processing 30, January 1993, p 65-83.

2. B. A. Carreras, B. P. van Milligen, M. A. Pedrosa, et al.: Experimental evidence of

long-range correlation and self-similarity in plasma ﬂuctuations. Phys. Plasmas 6,

1999, p 1885-1892.

3. Chuan Li, Ming LiangOil Debris, Signal Detection Based on Integral Transform and Empirical Mode Decomposition. World Academy of Science, Engineering and Technology 76, 2011, p. 190-194.

4. J. Theiler , S. Eubank , A. Longtin , B. Galdrikian and J. D. Farmer, Testing for nonlinearity in time series: The method of surrogate data. Physica D, vol. 58, 1992, p.77-94.

5. Г. Р. Аванесян, ОПРЕДЕЛЕНИЕ НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ СИГНАЛОВ ПО ИЗМИРЕНЯМ ВО ВРЕМЕННОЙ ОБЛАСТИ. Журнал Радиоэлектроники, 2, 2011, http://jre.cplire.ru/jre/feb11/5/text.html

6. В. И. Захаров, А. С. Зиенко, МЕТОДИКА СТАТИСТИЧЕСКОГО АНАЛИЗА ВЕЙВЛЕТ-СПЕКТРОВ ИОНОСФЕРНЫХ СИГНАЛОВ СИСТЕМИ GPS. Вестник Москоского Университета, Серия 3, Физика, Астрономия, Num 2, 2007, стр. 44-49

7. Jean-Marc Le Caillec, Rene Garello, Comparison of statistical indices using third order statistics for nonlinearity detection. Signal Processing 84, 2004, p. 499–525.

8. Subba Rao, T. Gabr, MA test for linearity of stationary time series analysis. J.Time Ser. Anal. 1, 1980, p. 145-158.

9. Hinich, M. J. Testing for Gaussianity and linearity of a stationary time series//

J. Time Ser. Anal. 3, 1982, p. 169-175.

10. Melvin J. Hinich, Detecting a Transient Signal by Bispectral Analysis. IEEE

Transactions on acoustics speech and signal processing vol 3 no 7, july 1990, p. 1277-1283

11. Melvin J. Hinich, On the Principal Domain of the Discrete Bispectrum of a Stationary Signal, IEEE Transactions on acoustics speech and signal processing vol 43 no 9, september 1995, p. 2130-2134

12. Choudhury, M. A. A. S., Thornhill, N. F. and Shah, S. L. Automatic Detection and Quantification of Control Valve Stiction, Control Engineering Practice, Vol. 14, issue 12, 2006, p. 1395-1412.

13. G. Z. dos Santos Lima, Z. O. Guimarães-Filho, A. M. Batista, I. L. Caldas, S. R. Lopes, R. L. Viana, I. C. Nascimento, Yu. K. Kuznetsov, Bicoherence in electrostatic turbulence driven by high magnetohydrodynamic activity in Tokamak Chauffage Alfvén Brésilien// PHYSICS OF PLASMAS 16, 2009, 04250 1-10.

14. B. Ph. van Milligen, C. Hidalgo, E. Sánchez, Nonlinear Phenomena and Intermittency in Plasma Turbulence. PHYSICAL REVIEW LETTERS, VOLUME 74, NUMBER 3, JANUARY 1995, p. 395-398.