УДК 621.396.677
СВЕРХРАЗРЕШЕНИЕ ПО ЧАСТОТЕ ПРИ ОБРАБОТКЕ РАДИОЛОКАЦИОННЫХ СИГНАЛОВ КОГЕРЕНТНЫМИ МЕТОДАМИ ЛИНЕЙНОГО ПРЕДСКАЗАНИЯ ВПЕРЕД-НАЗАД С ПРОРЕЖИВАНИЕМ ДАННЫХ
Д. С. Григорян
лаборатория проблем обработки радиолокационной информации
военной академии войсковой ПВО
имени маршала Советсвкого Союза А. М. Василевского, Смоленск
Получена 6
июля 2011 г.
Аннотация. Основываясь на анализе связи возмущений вектора весовых коэффициентов с числом обусловленности системы уравнений линейного предсказания, предложены методы формирования матриц данных с помощью предварительной обработки отсчетов с когерентным накоплением и прореживанием. Экспериментально с помощью обработки тестовых выборок показано преимущество когерентных методов линейного предсказания с прореживанием по сверхразрешению гармонических сигналов по сравнению с исходными методами спектрального анализа.
Ключевые слова: сверхразрешение, линейное предсказание, вектор весовых коэффициентов, обусловленность, спектральная функция.
Abstract. Be founded on weight vector disturbances connection with back-forward linear prediction equations conditionality number the methods of data matrix forming by samples primary processing with coherent accumulation are proposed. By test samples processing the preference of coherent linear prediction with decimation in harmonics superresolution in comparison with primary linear prediction methods is shown.
Keywords: superresolution, linear prediction, weight vector, conditionality, spectral function.
Введение
При проектировании современных радиолокационных систем различного назначения, как бортовых, так и наземных, большое внимание уделяется вопросам повышения их разрешающей способности по различным координатам и параметрам. Не во всех случаях удается достигнуть требуемых показателей разрешающей способности по угловым координатам из-за ограниченных размеров антенн или по частоте Доплера из-за ограниченности интервала наблюдения. Дополнительное увеличение размеров апертуры связано с техническими трудностями, а увеличение длительности выборки во многих случаях приводит к «размазыванию» спектра сигнала вследствие более быстрого изменения частот Доплера по сравнению с длительностью наблюдения. При обработке сигналов в когерентно-импульсных режимах работы локаторов разрешение по дальности ограничено шириной спектра радиосигналов, которая зачастую не может быть увеличена из-за аппаратных ограничений.
Приведенные противоречия заставляют многих исследователей искать способы сверхразрешения или по-другому «сверхрелеевского» разрешения радиолокационных сигналов. К настоящему времени в открытой зарубежной печати опубликован широкий спектр работ, описывающих различные подходы к сверхразрешению, которые весьма удачно обобщены в [1, 2]. Среди отечественных работ известны статьи Ширмана [3], Варюхина [4, 5], Курикши [6], Шинакова и Сперанского [7, 8], Фальковича и Коновалова [9], Черемисина [10, 11], Ермолаева [12], Дрогалина [13], Леховицкого [14], Слюсара [15] и многих других ученых [16–30], исследующих тематику сверхразрешения.
Одним из известных путей сверхразрешения радиолокационных сигналов является путь применения параметрических методов цифрового спектрального анализа, обобщенных в работах Марпла [1] и Стоицы [2]. Их достоинством считается эффект сверхразрешения, достигаемый при сравнительно небольших вычислительных затратах, не требующих перебора разных комбинаций параметров математических моделей сигналов для достижения заданного критерия эффективности. Однако эффект «расщепления» спектральных линий при обработке параметрическими методами зависит в первую очередь от отношения «сигнал/шум» (ОСШ), определяемого мощностью источников и длиной выборки, которые в условиях наблюдения радиолокационных сигналов не всегда достигают требуемых для сверхразрешения величин. Во вторую очередь сверхразрешение в параметрических методах зависит от способов формирования матриц данных, обоснование которых в цифровом спектральном анализе до сих пор носило эмпирический характер.
Для достижения высокой (сверхрелеевской) разрешающей способности методами спектрального анализа в радиолокации необходимы методы обработки ограниченных последовательностей данных, обеспечивающие при одинаковых ОСШ наилучшее разрешение.
Целью статьи является обоснование методов обработки данных, улучшающих по сравнению с известными авторегрессионными методами спектрального анализа разрешающую способность при одних и тех же ОСШ.
Обусловленность систем уравнений линейного предсказания
В одной из своих работ Савинов [22], основываясь на известном из линейной
алгебры условии единственности решений системы линейных уравнений [30], записал
для относительной нормы ![]() возмущений
возмущений ![]() вектора весовых
коэффициентов (ВВК) сигнального подпространства
вектора весовых
коэффициентов (ВВК) сигнального подпространства ![]() неравенство вида
неравенство вида
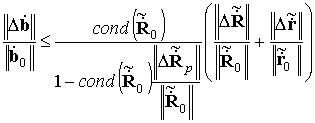 ,
(1)
,
(1)
в
котором ![]() – корреляционная матрица
(КМ) сигнального подпространства;
– корреляционная матрица
(КМ) сигнального подпространства;
![]() – возмущение КМ сигнального подпространства;
– возмущение КМ сигнального подпространства;
![]() – опорный вектор
(ОВ) сигнального подпространства;
– опорный вектор
(ОВ) сигнального подпространства; ![]() – возмущение ОВ сигнального подпространства;
– возмущение ОВ сигнального подпространства;
![]() – число
обусловленности КМ сигнального подпространства.
– число
обусловленности КМ сигнального подпространства.
Выборочные оценки КМ и ОВ, представляющие сумму КМ и ОВ сигнального подпространства и их возмущений, т. е.
![]() и
и ![]() .
.
В линейном предсказании вперед-назад с порядком авторегрессии P из выборки отсчетов ![]()
![]() формируются две
формируются две ![]() матрицы данных: ганкелева матрица
матрицы данных: ганкелева матрица
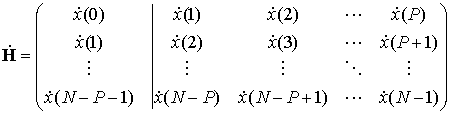
и тёплицева матрица
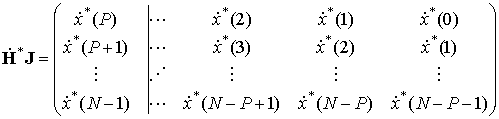
где ![]() – матрица замещения или обменная матрица
[1], у которой все элементы равны нулю, кроме элементов кросс диагонали, равных
единице.
– матрица замещения или обменная матрица
[1], у которой все элементы равны нулю, кроме элементов кросс диагонали, равных
единице.
Система уравнений линейного предсказания вперед-назад вида
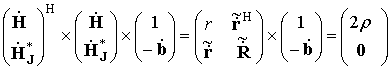 , (2)
, (2)
минимизирующая
методом наименьших квадратов средний квадрат ошибки линейного предсказания вперед-назад ![]() , связывает матрицы данных с выборочными оценками КМ и ОВ, где первый
элемент КМ в скобках
, связывает матрицы данных с выборочными оценками КМ и ОВ, где первый
элемент КМ в скобках ![]() представляет собой мощность выборки
данных. Из системы (2) может
быть получена система
представляет собой мощность выборки
данных. Из системы (2) может
быть получена система
где ![]() – КМ;
– КМ; ![]() – ОВ;
– ОВ;
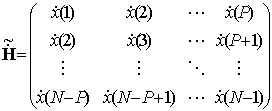 ;
;
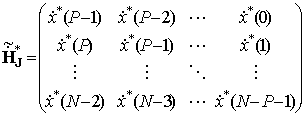 ;
;
– ганкелева и
тёплицева матрицы, полученные путем отделения первых столбцов матриц ![]() и
и ![]() ;
;
![]() и
и
![]()
– векторы свободных членов системы (3),
полученные из первых столбцов матриц ![]() и
и ![]() .
.
Представим
выборку отсчетов ![]() в векторно-матричной форме
в векторно-матричной форме
где ![]() – вектор комплексных экспонент M источников на частотах
– вектор комплексных экспонент M источников на частотах ![]() ;
;
![]() – вектор комплексных
амплитуд M источников.
– вектор комплексных
амплитуд M источников.
Матрицы ![]() ,
, ![]() и векторы
и векторы ![]() ,
, ![]() можно представить в виде
можно представить в виде
![]() ;
; ![]() ;
; ![]() ;
; ![]() ,
,
где 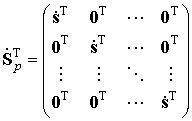 – блочная
– блочная ![]() матрица векторов амплитуд;
матрица векторов амплитуд;
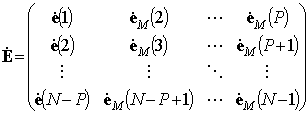 ,
,
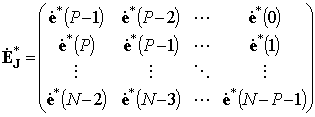
– блочные ![]() ганкелева и тёплицева матрицы
комплексных экспонент;
ганкелева и тёплицева матрицы
комплексных экспонент;
![]() ,
,
![]()
– векторы опорных комплексных экспонент, формирующих опорный вектор;
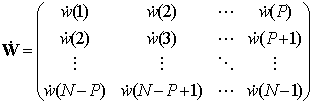 ,
,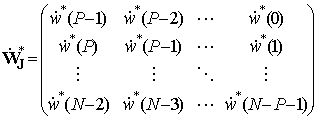
– ганкелева и тёплицева матрицы шумов;
![]() ,
, ![]()
–шумы вектора свободных членов.
Отсюда КМ и ОВ могут быть записаны в виде сумм
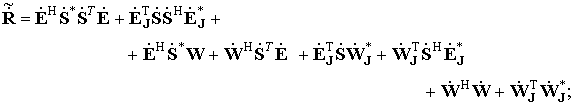 (5)
(5)
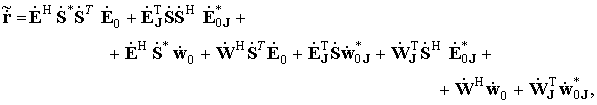 (6)
(6)
где первая строка (5) это КМ сигнального подпространства [30, 31], вторая – матрица комбинационных шумов, третья – КМ шумов. Аналогично первая строка (6) это ОВ сигнального подпространства, вторая строка – вектор комбинационных шумов, а третья строка (6) – вектор шумов.
При наличии шумов система (3) будет иметь вид
![]() , (7)
, (7)
откуда [29–31] получим возмущения ВВК в виде
![]() (8)
(8)
где ![]() – единичная матрица размером
– единичная матрица размером ![]() .
.
Обусловленность КМ сигнального
подпространства, определяется обусловленностью матрицы ![]() , откуда видно, что при классическом
предсказании вперед-назад, когда отсчеты удалены друг от друга на один элемент,
обусловленность плохая. Соответственно возмущения
, откуда видно, что при классическом
предсказании вперед-назад, когда отсчеты удалены друг от друга на один элемент,
обусловленность плохая. Соответственно возмущения ![]() ВВК
ВВК ![]() будут
велики. Для снижения обусловленности КМ сигнального подпространства в работе
предлагается применить методы прореживания отсчетов данных с когерентным
накоплением, суть которых поясняется ниже.
будут
велики. Для снижения обусловленности КМ сигнального подпространства в работе
предлагается применить методы прореживания отсчетов данных с когерентным
накоплением, суть которых поясняется ниже.
Когерентный фазовый метод линейного предсказания вперед-назад
с прореживанием отсчетов
В работе [1] Марпл
указывает, что наилучшим для линейного предсказания является порядок модели
авторегресии, равный от трети до половины количества отсчетов выборки. В задачах
цифровой обработки радиолокационных сигналов, как правило, имеют дело с
выборками по 32, 64, …, 512 отсчетов. Тогда для оптимального применения
линейного предсказания понадобиться оборачивать КМ размерностью от 10×10
до 256×256, что само по себе является сложной вычислительной процедурой.
Для того, чтобы с одной стороны снизить вычислительные затраты, а с другой
стороны улучшить обусловленность КМ сигнального подпространства, матрицы данных
![]() ,
, ![]() следует формировать
так, чтобы линейная зависимость строк и столбцов матриц
следует формировать
так, чтобы линейная зависимость строк и столбцов матриц ![]() ,
, ![]() , образующих матрицы данных, была
как можно меньше. Этого можно добиться с помощью прореживания отсчетов выборки
, образующих матрицы данных, была
как можно меньше. Этого можно добиться с помощью прореживания отсчетов выборки ![]() . Кроме того, для сохранения информации прореживание
можно организовать совместно с накоплением.
. Кроме того, для сохранения информации прореживание
можно организовать совместно с накоплением.
Выборку ![]() из N значений разобъем на Q субвыборок из N1 = N /Q отсчетов (рис.1). Когерентно суммируя отсчеты в
пределах каждой q-й субвыборки
с помощью операции
из N значений разобъем на Q субвыборок из N1 = N /Q отсчетов (рис.1). Когерентно суммируя отсчеты в
пределах каждой q-й субвыборки
с помощью операции
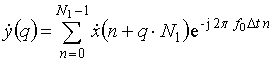 , (9)
, (9)
получим Q значений отсчетов вторичной выборки, где ![]() номер отсчета
прореженной выборки;
номер отсчета
прореженной выборки; ![]() –
резонансная частота полосовых фильтров предварительной обработки (ФПО). Резонансная
частота ФПО
–
резонансная частота полосовых фильтров предварительной обработки (ФПО). Резонансная
частота ФПО ![]() ,
определяющая импульсную характеристику вида
,
определяющая импульсную характеристику вида ![]() , выбирается равной частоте максимума
дискретного преобразования Фурье (ДПФ) всей выборки
, выбирается равной частоте максимума
дискретного преобразования Фурье (ДПФ) всей выборки ![]() .
.
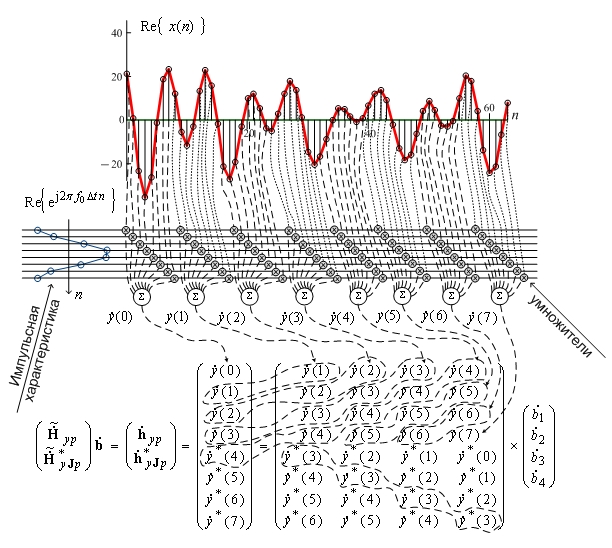
Рис. 1. Схема формирования матриц данных из выборки размером 64 отсчета с прореживанием до 8 отсчетов с когерентным накоплением по 8 отсчетов.
Комплексная частотная характеристика (КЧХ) ФПО будет определяться как
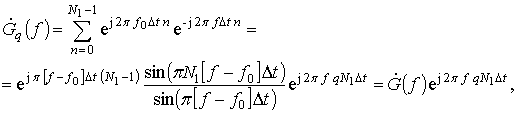 (10)
(10)
где 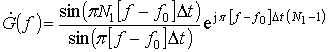 – часть КЧХ, идентичная для всех ФПО. Амплитудно-частотные
характеристики (АЧХ) ФПО одинаковые и имеют вид функции sinN1x/sinx, а отличия фазо-частотных характеристик (ФЧХ) определяются задержками
– часть КЧХ, идентичная для всех ФПО. Амплитудно-частотные
характеристики (АЧХ) ФПО одинаковые и имеют вид функции sinN1x/sinx, а отличия фазо-частотных характеристик (ФЧХ) определяются задержками ![]() .
.
По аналогии с (4) отсчеты вторичной выборки в векторно-матричной форме могут быть представлены как
![]() , (11)
, (11)
где ![]() – вектор КЧХ каналов первичной обработки;
– вектор КЧХ каналов первичной обработки;
![]() – вектор прореженных комплексных
экспонент;
– вектор прореженных комплексных
экспонент;
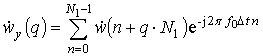 – шум с выхода каналов первичной
обработки.
– шум с выхода каналов первичной
обработки.
Для
порядка модели P из отсчетов прореженной выборки (рис.1) составим матрицы ![]() и
и ![]() размером
размером ![]()
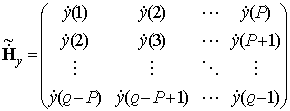 ,
,
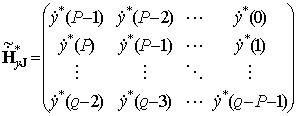 ,
,
а также векторы свободных членов ![]() и
и ![]()
![]() и
и ![]() .
.
По методу наименьших квадратов ВВК определим из системы
![]() ,
,
где ![]() – корреляционная матрица вторичных отсчетов;
– корреляционная матрица вторичных отсчетов;
![]() – опорный вектор
определяемые ниже как
– опорный вектор
определяемые ниже как
![]() ;
; ![]() ;
;
![]() ;
; ![]() ,
,
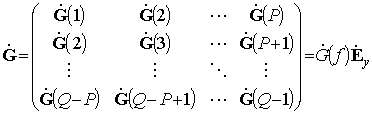 ,
,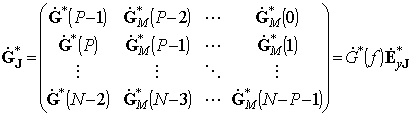
– блочные ![]() ганкелева и тёплицева матрицы
КЧХ ФПО, характеризующие изменение фазы гармоник с разными частотами от одного
прореженного отсчета к другому при выполнении процедуры предсказания
вперед-назад;
ганкелева и тёплицева матрицы
КЧХ ФПО, характеризующие изменение фазы гармоник с разными частотами от одного
прореженного отсчета к другому при выполнении процедуры предсказания
вперед-назад;
![]() и
и ![]() – матрицы прореженных комплексных
экспонент размером
– матрицы прореженных комплексных
экспонент размером ![]() ,
аналогичные матрицам
,
аналогичные матрицам ![]() ,
,
![]() .
.
![]() ;
;
![]() ,
,
– векторы опорных КЧХ, формирующих опорный вектор;
![]() и
и ![]() – векторы опорных прореженных комплексных
экспонент, формирующих опорный вектор, аналогичные векторам
– векторы опорных прореженных комплексных
экспонент, формирующих опорный вектор, аналогичные векторам ![]() и
и ![]() ;
;
![]() ,
,![]()
–шумы вектора свободных членов. Спектральная функция линейного предсказания имеет вид
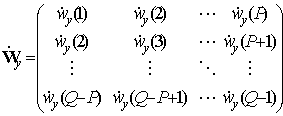 ,
,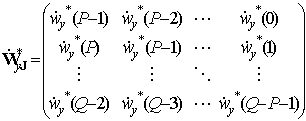 ,
,
– ганкелева и тёплицева матрицы шумов;
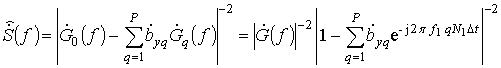 .
.
Для когерентного метода линейного предсказания вперед-назад с прореживанием КМ и ОВ можно представить в виде
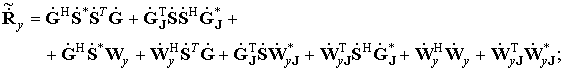 (12)
(12)
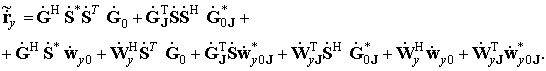 (13)
(13)
Анализ (12) показывает, что КМ сигнального подпространства
![]() (14)
(14)
имеет обусловленность лучшую, чем КМ ![]() , определяемая из (5).
Это определяется лучшей обусловленностью
, определяемая из (5).
Это определяется лучшей обусловленностью ![]() и
и ![]() по сравнению с матрицами
по сравнению с матрицами ![]() и
и ![]() исходного метода, так как имеет
место прореживание отсчетов в N1 раз.
исходного метода, так как имеет
место прореживание отсчетов в N1 раз.
Когерентный фазовый метод линейного предсказания вперед-назад с прореживанием движущимся окном
Приведем
еще одну модификацию когерентного фазового метода обработки данных с
прореживанием, использующий ФПО количеством на один больше порядка модели. Выходные
отсчеты каждого из ФПО формируются путем смещения импульсной характеристики
ФПО, длиной в ![]() отсчетов, на один отсчет вправо (рис. 2). Количество
смещений определяется формулой
отсчетов, на один отсчет вправо (рис. 2). Количество
смещений определяется формулой
![]() , (15)
, (15)
где ![]() .Выходные
k-е отсчеты (k=0..K) каждого p-го ФПО определяются
как
.Выходные
k-е отсчеты (k=0..K) каждого p-го ФПО определяются
как
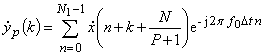 . (16)
. (16)
Этот метод формирования матриц данных практически при той же обусловленности КМ сигнального подпространства позволяет формировать ФПО с неидентичными КЧХ. Это даёт возможность использовать кроме фазовых отличий КЧХ еще и амплитудные отличия.
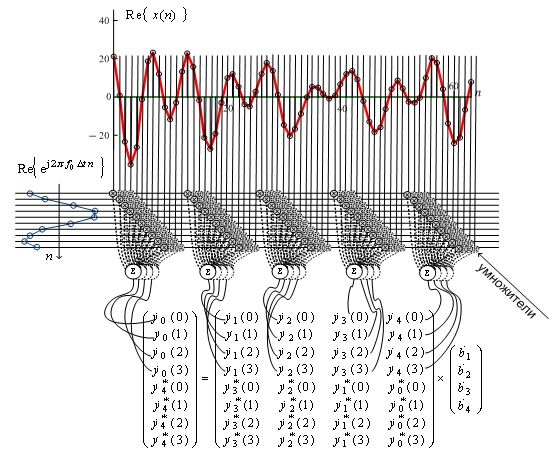
Рис. 2. Схема формирования матриц данных из выборки размером 64 отсчета с прореживанием движущимся окном до 8 отсчетов с когерентным накоплением по 8 отсчетов.
Результаты экспериментов с тестовыми выборками
Для сравнительного анализа была рассмотрена тестовая последовательность 64-х отсчетов данных, состоящих из смеси четырех гармоник на частотах 6250 Гц, 6350 Гц, 6700 Гц и 3000 Гц (для второго когерентного метода 1000 Гц). Ширина релеевского элемента разрешения, определяемого шириной главного лепестка ДПФ, составляла 687 Гц. В первом случае был рассмотрен исходный подход линейного предсказания вперед-назад с порядком модели P=20, а во втором и третьем случаях была выполнена когерентная обработка данных двумя приведенными выше методами. Резонансная частота ФПО была выбрана 6200 Гц. При использовании первого метода длина импульсной характеристики составляла N1 = 8. При использовании второго метода длина импульсной характеристики ФПО составила 10 отсчетов, а количество самих ФПО было равно 5 (рис. 2). В первом случае выполнялось прореживание выборки по 8 элементов. Во втором случае с выхода каждого из ФПО были получены по 4 отсчета, после чего составлялась матрица данных. На рисунке 3, 4 и 5 показана спектральная функция линейного предсказания исходного метода и приведенных когерентных методов обработки
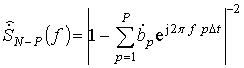 и
и
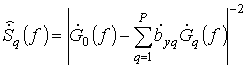 .
.
Кроме того на графиках показаны амплитуды источников, вычисленные по частотам, определяемым через корни характеристических полиномов вида
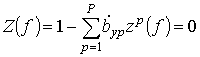 ,
,
где для исходного метода ![]() , а для когерентных
методов
, а для когерентных
методов ![]() Вычисление
амплитуд источников выполнялось решением обратной задачи. Для оценок частот
Вычисление
амплитуд источников выполнялось решением обратной задачи. Для оценок частот ![]() определялась матрица
определялась матрица
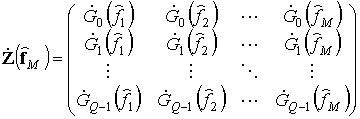 и вектор
и вектор
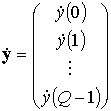 ,
,
связанные системой уравнений
![]() , откуда
, откуда ![]() .
.
На рисунках 3, 4 и 5 приведены 200 реализаций спектральных функций, полученных каждый раз при разных шумах. Анализ рисунков 3, 4 и 5 показывает, что спектральные функции когерентных методов с прореживанием обладают большей разрешающей способностью, чем спектральные функции исходного метода линейного предсказания. На спектральной функции исходного метода гармоники с частотами 6250 Гц и 6350 Гц не разрешаются (рис. 3), в то время как на спектральных функциях когерентных методов эти гармоники в большинстве случаев разрешались по спектральной функции, а корни характеристических полиномов находились в окрестности истинных частот (рис. 4 и 5). Исходное ОСШ было задано 45 дБ. Учитывая длину выборки в 64 отсчета, следует считать еще и прирост ОСШ до 18 дБ за счет накопления энергии.
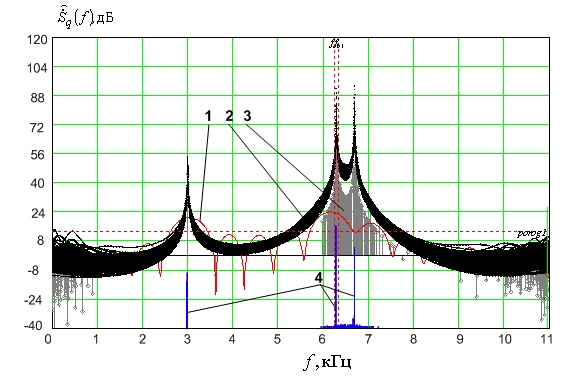
Рис.3. Спектральные функции исходного метода линейного предсказания:
ДПФ выборки –1; ансамбль спектральных функций, полученных по 200 реализациям – 2; оценки амплитуд, соответствующих корням характеристического полинома, полученных по 200 реализациям – 3, гистограммы распределения оценок частот корней характеристического полинома –4.
Вероятность совместного разрешения первой и второй гармоник для классического метода при исходном ОСШ 45 дБ была равна нулю, а для когерентных методов составила 0,81. Исходный метод линейного предсказания в тестируемых ситуациях достигает для разности частот 100 Гц при ширине релеевского элемента 687 Гц таких же показателей эффективности при ОСШ 55 дБ как и когерентные методы при 45 дБ. Анализ вычислительных затрат показывает также явное преимущество когерентного метода, так как требуемый порядок модели когерентных методов был равен 4 в то время как для исходного метода он составлял 20, что было равно почти трети количества отсчетов [1].
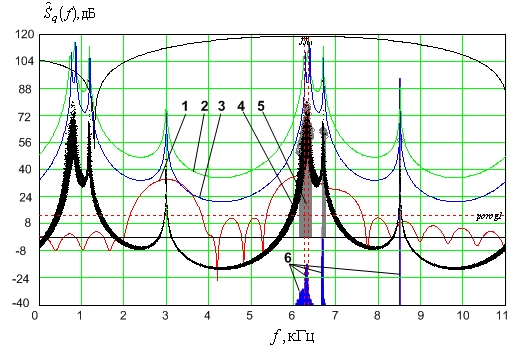
Рис.4. Спектральные функции когерентного метода с прореживанием:
ДПФ выборки –1; одна из реализаций спектральной функции –2 (график приподнят на 30 дБ); математическое ожидание спектральных функций 3 (график приподнят на 46 дБ); семейство спектральных функций, полученных по 200 реализациям – 4; оценки амплитуд, соответствующих корням характеристического полинома, полученных по 200 реализациям –5; гистограммы распределения оценок частот корней характеристического полинома –6.
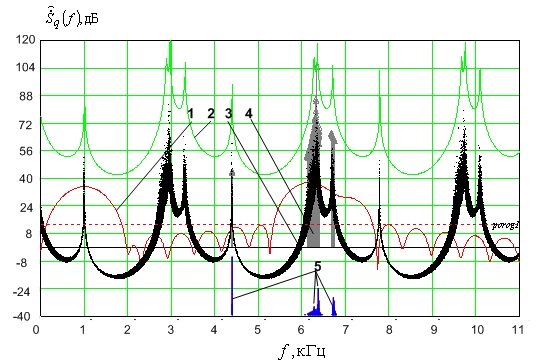
Рис.5. Спектральные функции когерентного метода с прореживанием движущимся окном:
ДПФ выборки –1; одна из реализаций спектральной функции –2 (график приподнят на 30 дБ); семейство спектральных функций, полученных по 200 реализациям – 3; оценки амплитуд, соответствующих корням характеристического полинома, полученных по 200 реализациям –4; гистограммы распределения оценок частот корней характеристического полинома –5.
Следует отметить, что разность частот в 100 Гц между первой и второй гармониками на частотах 6250 Гц и 6350 Гц составляла почти седьмую долю ширины главного лепестка АЧХ фильтра ДПФ. Присутствие третьей гармоники на частоте 6700 Гц заметно ухудшало обусловленность системы уравнений линейного предсказания, что потребовало для разрешения гармоник около 45 дБ исходного ОСШ. Для разрешения источников с частотами, разность которых составляет от половины до трети ширины лепестка АЧХ фильтра ДПФ, требуется гораздо меньшее ОСШ от 15 до 20 дБ. Конечно же, следует привести результаты разрешения для разных ОСШ и разных вероятностей с учетом дисперсий оценок самих частот. Учитывая ограниченность объема статьи, данные материалы не включены в текст. Однако проведенные исследования показывают явное преимущество когерентных методов спектрального анализа по сравнению с классическими подходами.
Основным недостатком данного когерентных методов с прореживанием является повторение спектральных линий, возникающее из-за прореживания данных, когда частота следования отсчетов после прореживания становится меньше частот самих гармоник, т. е. происходит нарушение условий теоремы Котельникова. Однако для радиолокационных задач предварительная фильтрация сигналов с помощью операций прямого и обратного ДПФ устраняет паразитное влияние сигналов помех, часоты которых лежат далеко за пределами рассматриваемого строба частоты, определяемого шириной фильтра ДПФ.
Заключение
Подводя итоги, следует отметить, что приведенный в статье когерентный подход может быть использован при обработке сигналов и формировании матриц данных в пространственной области и при обработке сигналов с перестройкой частоты при переходе из частотной области во временную при построении дальностных портретов. Основная идея данного подхода базируется на том, что после предварительной когерентной обработки данных их матрица формируется из отсчетов с выходов фильтров, КЧХ которых сильно отличаются друг от друга по фазе благодаря чему число обусловленности идеальной корреляционной матрицы меньше чем в исходном подходе. При этом выигрыш по сверхразрешению достигается меньшим числом обусловленности КМ сигнального подпространства. Исследование показало, что из-за лучшей обусловленности КМ приведенный когерентный подход обеспечивает сверхразрешение при более низких ОСШ (почти на 10 дБ при разности частот около седьмой доли ширины релеевского элемента) чем исходный подход линейного предсказания, а также лучшую чувствительность к наличию или отсутствию гармоник в смеси сигнала и шума, по сравнению с подобными когерентными методами описанными в [20] и [21].
Полученная когерентным методом с прореживанием корреляционная матрица может быть использована такими методами анализа как MUSIC, EV, ESPRIT и другими спектральными методами, обеспечивающими сверхразрешение.
В заключение автор выражает благодарность профессору В. В. Абраменкову и Ю.И.Савинову за плодотворные дискуссии, позволившие лучше осмыслить вопросы данной тематики и более качественно подготовить материал.
Литература
1. Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения / Пер. с англ. М.: Мир, 1990.
2. Stoica P, Moses R. L. Introduction to Spectral Analysis. New Jersey, Prentice-Hall, Inc. 1997, 319 p.
3. Ширман Я. Д. Разрешение и сжатие сигналов. М.: «Сов. Радио», 1974, 360 с.
4. Варюхин В. А., Покровский В. И., Сажно В. Ф. О точности измерения угловых координат нескольких источников с помощью антенной решетки// Радиотехника и электроника. 1984. № 4.
5. Варюхин В. А. Основы теории многоканального анализа. – Киев, ВА ПВО СВ им. А. М. Василевского. 1993.
6. Курикша А. А. Оценка числа и параметров компонент сигнала при наличии шума// Радиотехника и электроника, 1984. №9. С. 1740-1744.
7. Шинаков Ю. С., Сперанский В. С. "Совместное обнаружение, разрешение и измерение параметров сигналов на фоне помех на выходе антенной решетки. Синтез алгоритмов", "Радиотехника и электроника", 1982, т. 27, № 11, с. 2179-2184.
8. Шинаков Ю. С. "Совместное обнаружение и разрешение неизвестного числа сигналов", "Радиотехника и электроника", 1985, т. 30, №6, с. 1131-1138.
9. Фалькович С. Е., Коновалов Л. Н. "Разрешение неизвестного числа сигналов"", "Радиотехника и электроника", 1982, т. 27, № 1, с. 92-97.
10. Черемисин О. П. "Адаптивные методы определения числа и пространственных параметров сигналов в многоканальных приемных системах", "Радиотехника и электроника", 1986, т. 31, № 3, с. 499-508.
11. Черемисин О. П. Эффективность адаптивных методов пеленгации помех// Радиотехника и электроника. 1989. Т. 34, № 9. С. 1850–1857.
12. Ермолаев В.Т., Родыгин Ю.Л., Флаксман А.Г. Методы определения вектора пространственной адаптивной обработки при короткой выборке помехи // Изв. Вузов. Радиофизика. 1994. Т.37, № 4. С. 493-509.
13. Дрогалин В.В. Алгоритмы оценивания угловых координат источников излучений, основанные на методах спектрального анализа. /В.В. Дрогалин и др.. // Успехи современной радиоэлектроники. 1998. №2. — 3-17
14. Леховицкий Д. И., Флексер П. М., Атаманский Д. В., Кириллов И. Г. Статистический анализ некоторых «сверхразрешающих» методов пеленгации источников шумовых излучений в антенных решетках при конечном объеме обучающей выборки//Антенны, 2000, №2, с. 23–39.
15. Слюсар В. И. Интерпретация метода Прони для решения дальномерных задач// Радиоэлектроника: Изв. Вузов. 1998. № 1. С. 61–67.
16. Царьков Н. М. Многоканальные радиолокационные измерители. М., Сов. радио, 1980.
17. Ратынский М. В. Адаптация и сверхразрешение а антенных решетках – М.: Радио и связь, 2003. – 200 с.
18. Абраменков В. В. Накопление сигнала при использовании современных методов спектрального анализа// Радиотехника. 2002. № 12. С. 88–91.
19. Абраменков В. В., Жибуртович Н. Ю., Климов С. А., Савинов Ю. И., Чижов А. А. Оценка влияния искажений характеристик направленности элементов антенных решеток на эффективность измерения угловых координат методом Прони// Информационно-измерительные и управляющие системы, 2005. Т.3. №6. С. 36-41.
20. Савинов Ю. И. Когерентный метод Прони с квазипрореживанием// Вопросы радиоэлектроники. Серия РЛТ. Вып. 3, 2008 - С. 122-128.
21. Абраменков В. В. Измерение угловых координат М источников излучения методом нормирования сигнала к амплитудам образовавших его источников//Сб. статей. Авионика 2002 – 2004. М.: Радиотехника, 2005. С. 218 – 221.
22. Савинов Ю. И. Метод Прони. Смоленск: ВА ВПВО ВС РФ им. А. М. Василевского, 2008, 87 с.
23. Нечаев Ю.Б. Метод оценки количества сигналов в задачах радиопеленгации при небольшом времени наблюдения / А. Зотов, Ю.Б. Нечаев // Изв. вузов. Радиоэлектроника. — 2008. — № 6 — 3-9.
24. Аджемов С. Исследование алгоритмов сверхразрешения в адаптивных антенных решетках. / С. Аджемов, Г.О. Бокк, А.Г. Зайцев и др.. // Радиотехника. — 2000. —№11. — 66-71.
25. Сычев М.И. Пространственно-временная обработка радиосигналов на основе параметрического спектрального анализа // Антенны. — 2001. — вып. 1(47). — С . 70-77.
26. Добырн В.В. Эффективность применения сверхразрешающих спектральных оценок в бортовых угломерных фазированных антенных решетках /В.В. Добырн, А.В. Немов // Радиотехника. — 1999. — №9. 65-67.
27. Ганков И.В. Предельные характеристики сверхразрешения когерентных источников при предварительной декорреляции выборки. Радиотехника, 1994. — №10. — 23-27
28. Григорян Д. С. Определение области сверхразрешения источников излучения по пространству при собственных шумах и неидентичностях приемных трактов// Радиотехника. 2007. № 8. С. 43–48.
29. Григорян Д. С. Влияние неидентичностей амплитудно-частотных характеристик приемных каналов цифровой антенной решетки на возможность сверхразрешения источников излучения по пространству// Радиотехника. 2009. № 10. С. 27–36.
30. Беклемишев Д. В. Дополнительные главы линейной алгебры. М.: Наука. Главная редакция физико-математической литературы, 1983. – 336 с.
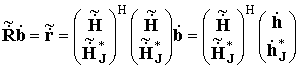 ,
(3)
,
(3)