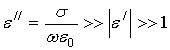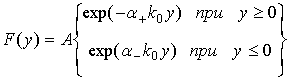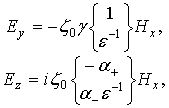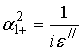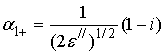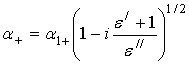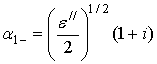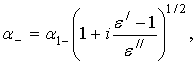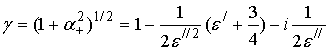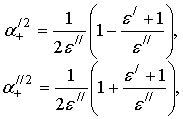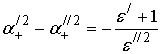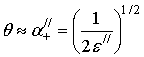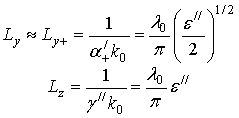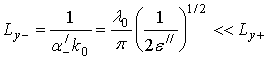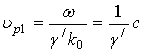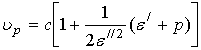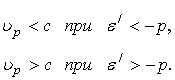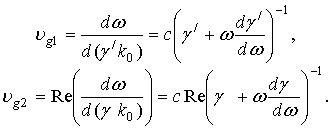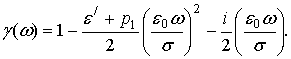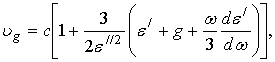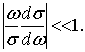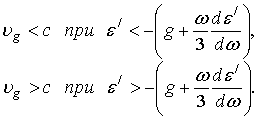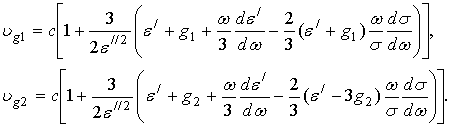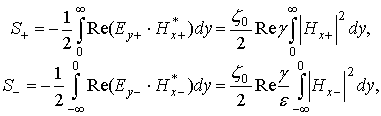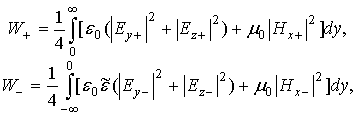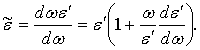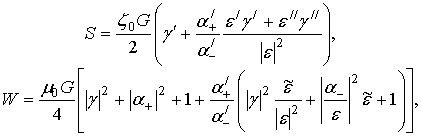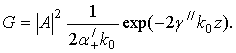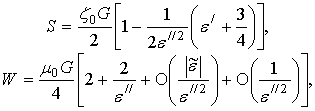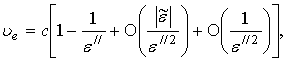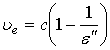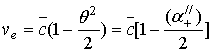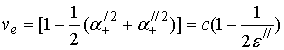Поверхностные электромагнитные волны на плоских границах электропроводящих сред с высокой проводимостью, волна Ценнека

УДК 538.566.2: 621.372.8

В. В. Шевченко
Институт радиотехники и электроники им. В.А.Котельникова РАН

Получена 25 июля 2013 г.

Аннотация. Рассмотрены свойства теоретической модели поверхностных электромагнитных волн, направляемых плоскими границами высоко проводящих сред: металлов, влажной почвы, морской и вообще соленой воды. Вычислены фазовая, «групповая» и энергетическая скорости таких волн. Показано, что эти волны относятся к необычному типу волн, у которых «групповая» скорость отличается от энергетической скорости, т.е. скорости переноса волной энергии. И хотя в зависимости от параметров среды фазовая и «групповая» скорости таких волн могут быть больше скорости света с, их энергетическая скорость всегда меньше скорости света. К рассмотренному типу волн относится так называемая волна Ценнека.

Ключевые слова: поверхностные волны; фазовая, групповая, энегетическая скорости волн; волна Ценнека.

Abstract.The properties of a theoretical model of surface electromagnetic waves, guided by the plane boundaries of high conductive media: metals, humid soils, sea and salty water in general are considered. The phase,”group” and energy flow velocities of these waves are calculated. These waves are related to the unusual type of waves, the “group” velocity of which is differed from the energy flow velocity, that is the wave energy transport velocity. Although depending on medium parameters the phase and “group” velocities of these waves can be more than the light velocity c, their energy flow velocity always less than the light velocity c. So named Zenneck’s wave is related to considered the type of waves.

Key words: surface waves; phase, group, energy flow velocities of waves; Zenneck’s wave.

Введение

Вопрос об указанных в названии статьи поверхностных волнах и, в особенности, о так называемой волне Ценнека в течение многих лет время от времени, снова и снова поднимается в научных дискуссиях в области прикладной электродинамики, как теоретиками, так и экспериментаторами. Поскольку такие дискуссии отражены во многих публикациях (см., например, в [1-11] и лит. ссылки в них), то здесь мы не останавливаемся на деталях опубликованных утверждений и сомнений. Отметим только, что обычно обсуждаются следующие вопросы. Возможна ли вообще с физической точки зрения волна Ценнека: не противоречит ли это физическим законам, а если возможна, то можно ли ее возбудить физически реализуемыми источниками и можно ли ее использовать для передачи сигнала в системах связи и в радиолокации.

Представленный ниже теоретический анализ даёт, по мнению автора, вполне определенный ответ, по крайней мере, на первые два из указанных вопросов, т.е. не противоречит и можно ее возбудить. Оставшийся вопрос относится к области технологии реализации и применения таких поверхностных волн.

1. Основные свойства поверхностной волны на плоской границе высоко проводящей среды

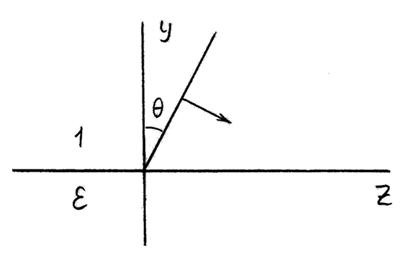
Пусть зависимость стационарного электромагнитного поля от времени имеет вид , где - круговая частота поля. Рассмотрим для простоты, как это делается обычно [4,10], двумерную модель (результаты легко переносятся на трехмерную модель [11]) электромагнитной поверхностной волны на плоской границе (Рис.1) между свободным пространством с параметрами , и электропроводящей немагнитной () средой с эффективной диэлектрической проницаемостью , где комплексная безразмерная относительная проницаемость

. (1)

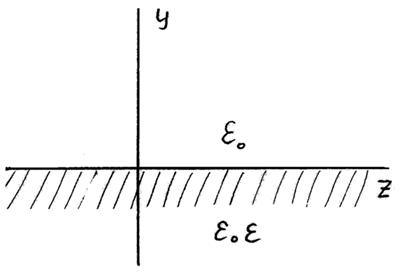
Рис. 1. Плоская граница электропроводящей среды

При этом будем считать, что для рассматриваемой среды выполняются соотношения

, . (2)

Например, для влажной почвы, морской и просто соленой воды () в радиоволновом диапазоне, а для металлов () в радиоволновом диапазоне, СВЧ, КВЧ и вплоть до инфракрасного диапазона оптических частот

, (3)

где - удельная проводимость среды [12-14].

Комплексные магнитную и электрические компоненты поля поверхностной волны соответствующей поляризации, распространяющейся вдоль плоской границы среды в направлении оси z (Рис.2), представим в виде

, (4)

, (5)

(6)

где А – амплитудная константа, 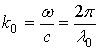, с – скорость света и - длина волны в свободном пространстве, ,

, ,

, (7)

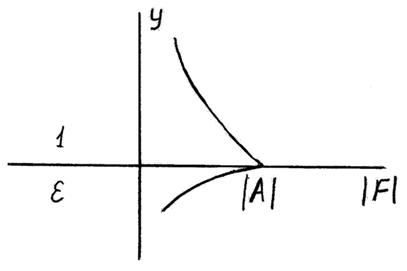
Рис. 2. Локализация поля волны около границы среды

Исходное дисперсионное уравнение, получаемое при сшивании поля на границе среды при y=0 согласно равенствам

, , (8)

имеет вид

, (9)

или на основании (7) –

. (10)

Приближенное уравнение и его решение при имеют вид

, (11)

,, (12)

а уточненное уравнение и его решение при , т.е. согласно (12) –

, . (13)

На основании этих соотношений и выражений (7), (9) вычисляются значения

, (14)

. (15)

Таким образом, волна действительно является поверхностной, поскольку , , и она распространяется вдоль границы y=0 в направлении оси z.

Следует отметить, что результат (15) может быть получен также из соотношения

, (16)

где

(17)

которое позволяет проанализировать структуру поля волны, соответствующую выражениям (4), (5).

Действительно, величина , описывающая прижатие поля волны к границе среды, согласно (16) увеличивает значение , что замедляет скорость движения фазового фронта волны, а величина , описывающая наклон фазового фронта волны к границе среды (Рис. 3, физическая причина наклона состоит в том, что среда частично поглощает энергию волны) уменьшает значение , то есть ускоряет движение фазового фронта волны вдоль границы.

Рис.3. Наклон фронта волны к границе среды

При этом при значениях этих величин, соответствующих выражениям (17), старшие по малой величине члены в (16) компенсируются, так что

, (18)

и в результате в вещественной части в (15) остаются только члены, пропорциональные квадрату этой малой величины. Отмеченный выше наклон направления распространения фазового фронта волны к границе среды (Рис.3), согласно сказанному, составляет малый угол

. (19)

Выражения (12),(13),(15) позволяют оценить протяженности поля поверхностной волны в поперечном (L_y) и продольном (L_z)направлениях, которые приближенно равны

(20)

Здесь не учитывается малая поперечная протяженность поля волны внутри среды, равная согласно (14)

. (21)

Из соотношений (20) следует, что , т.е. волновое поле имеет существенно бόльшую протяженность, стремящуюся при в бесконечность в продольном направлении, т.е. вдоль границы, быстрее чем в поперечном. Следовательно, это поле представляет собой направляемую поверхностную волну, распространяющуюся вдоль границы среды.

Иногда [9,10] поле рассматриваемых направляемых поверхностных волн ошибочно качественно отождествляется с ненаправляемым полем пространственной волны в области плоской границы слабо поглощающего диэлектрика с , .

Действительно, выражения для параметров поля такой волны, представленные в [10], имеют вид

(22)

где . Из этих выражений в пределе при т.е. для не поглощающего диэлектрика, и при любом конечном значении получим не направляемое пространственное поле для плоской волны, падающей на границу диэлектрика под углом Брюстера:

(23)

В частности в пределе при , т.е. для свободного пространства, получим вместо направленной вдоль бывшей границы диэлектрика плоской волны с параметрами .

В отличие от этого из полученных в (12)-(15) выражений для рассматриваемых поверхностных волн в пределе при т.е. при отсутствии потерь энергии волн, и при любом конечном значении имеем , что соответствует направленной плоской волне рассматриваемой поляризации, распространяющейся вдоль плоской границы среды с предельно большой проводимостью.

2. Фазовая скорость

Скорость как физическая величина, характеризующая процесс движения, в данном случае волны, имеет физический смысл только, если она вещественная. Поэтому, в соответствии с (4) в случае комплексного значения относительного продольного волнового числа (7) рассмотрим приближенную фазовую скорость волны в двух равноправных вариантах:

(24)

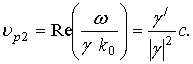
Для рассматриваемой волны, согласно (15), полученные из этих выражений результаты можно объединить и представить в виде

, (25)

где в соответствии с (23) или согласно (24). При условии (3) здесь выполняется соотношение .

Из выражения (25) следует, что

(26)

3. Групповая скорость

Формально вводимую групповую скорость аналогично фазовой рассмотрим в двух видах:

(27)

Для раскрытия этих выражений необходимо знать функцию , которую используя зависимость (3) на основании (15) получим в виде

(28)

Подстановка этого выражения в (27) после преобразования дает

(29)

где , . Здесь учтено, что для влажной почвы, морской и просто соленой воды и для металлов на указанных выше частотах проводимость почти не зависит от частоты [12-14]. Поэтому в выражение (29) не включен член, содержащий в качестве сомножителя величину

(30)

Из результата (29) следует, что

(31)

Фазовой и групповой скоростям волны Ценнека соответствуют вторые соотношения в (26) и (31).

С учетом члена, содержащего (30), введенные выше групповые скорости равны

(32)

Здесь следует отметить, что переходы значений фазовой и групповой скоростей волн через скорость c происходят при отличающихся параметрах среды. Учитывая приближенный характер введенных скоростей, нет основания придавать какой либо физический смысл полученным конкретным значениям переходных параметров среды.

4. Энергетическая скорость

Энергетическая скорость, т.е. скорость передачи волной энергии [4,13,15], может быть вычислена по следующей уточненной здесь формуле:

, (33)

где усредненные по времени - продольный (вдоль оси z) поток переносимой волной мощности и – перемещаемая вместе с волной линейная плотность энергии на единицу длины вдоль направляющей структуры, т.е. плоской границы (также вдоль оси z). Такая кинематически определяемая энергетическая скорость основана на теореме Умова- Пойнтинга. Она применима как к волнам, распространяющимся без потерь энергии, так и к волнам с потерями. Это определение не включает диссипативную и поглощаемую средой энергию, которая не распространяется вместе с волной. При этом выполняется баланс перемещаемой волной энергии вдоль границы среды.

Для рассматриваемой волны имеем

, (34)

где и - парциальные потоки мощности над и под плоскостью y=0, которые согласно (4), (6) равны

(35)

и, соответственно , где при м имеем

(36)

(37)

Подставив под интегралы в (35), (37) выражения (4)-(6), после вычисления интегралов получим

(38)

где

(39)

На основании (12)-(15) эти выражения можно преобразовать к виду

(40)

откуда следует, что

(41)

Здесь под выражениями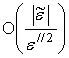, 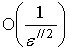понимаются малые значения функций, порядки величин которых соответствуют указанным от параметров среды аргументам при .

Из результата (41), сохраняя только старшие члены, получим

. (42)

В дополнение к простому, по здравому смыслу введенному выше определению энергетической скорости волны в качестве его подтверждения и уточнения приведем здесь еще иное, что называется «на пальцах», вычисление этой скорости для рассматриваемых поверхностных волн.

Специфика волн, направляемых волноведущими структурами (не следует путать с волнами, направленными источниками поля), здесь границей высоко проводящей среды, заключается в важном отличии их свойств от свойств волн в однородных средах. Структура их поля и дисперсионные свойства определяются не только материальными параметрами среды и, следовательно, материальной дисперсией, т.е. частотной дисперсией параметров, но и так называемой структурной дисперсией волн, зависящей от геометрической структуры (неоднородности) направляющей среды. Хорошо известен пример направляющей системы, формирующей структуру поля и дисперсию волн вообще без учета материальной дисперсии: это полые волноводы с идеально отражающими стенками.

В полых волноводах угол наклона фазового фронта так называемых плоских волн Бриллюэна, образующих направляемую волноводом волну, позволяет вычислить энергетическую скорость волны [4,13,15] в виде

. (43)

На основании этого выражения и формулы (19) получим для рассматриваемых здесь поверхностных волн

, (44)

где - фазовая, а при малых значениях она же энергетическая скорость [15] замедленной поверхностной волны в направлении движения фазового фронта. В результате на основании (17) получим

. (45)

По существу в проведенном вычислении было использовано свойство волн с плоским фазовым фронтом, применимое к плоским и близким к ним волнам, состоящее в том, что наклон направления движения фазового фронта по отношению к направлению распространения волны увеличивает фазовую скорость (15), (16), (24) и уменьшает энергетическую скорость (45) волны.

Из сравнения результатов (42) и (45) видно, что они совпадают с качественной точки зрения, т.е. в том же порядке по малой величине . Уже из этого следует важный для нашего рассмотрения результат, что энергетическая скорость рассматриваемых волн меньше скорости света с.

Что касается количественной стороны, то какой из этих результатов является более правильным зависит от того считать ли плотность энергии волны в среде под границей перемещаемой вместе с волной или нет. Если бы выше при вычислении энергетической скорости в формулах (38)-(40) не учитывалась плотность энергии поля в среде под границей, например, как при решении задачи с использованием импедансного граничного условия М.А. Леонтовича, то в том же порядке приближения был бы получен вместо (42) результат (45). При этом отметим, что поток мощности в среде в направлении вдоль границы согласно (38) оказался пропорциональным , т.е. он не учитывался. Из этого факта и, как это известно, из условия М.А. Леонтовича следует, что поток мощности направлен в среде почти ортогонально к границе, т.е. правильно считать, что энергия поля в среде не перемещается в направлении распространения волны, а просто поглощается в среде. Таким образом, правильным для энергетической скорости волны является результат (45).

В итоге имеем, что энергетическая скорость поверхностной волны всегда меньше с, включая случай, соответствующий волне Ценнека, для которой фазовая и групповая скорости оказываются больше с.

5. Обсуждение результатов

Обсудим критически известные версии, на основании которых, казалось бы, можно утверждать, что рассмотренная выше теоретическая модель поверхностных волн не описывает физические поверхностные волны, направляемые границей электропроводящей среды с высокой проводимостью в случае, когда фазовая и/или групповая скорости оказываются больше скорости света с.

Версия 1. Известно [4,10,11,16], что если фазовая скорость волны больше скорости света, то волна не может направляться открытой направляющей структурой, а должна высвечиваться в свободное пространство, т.е. она является, так называемой, вытекающей волной. Однако, согласно полученной выше функции поля волны и рис.3, распространение фронта волны направлено не в пространство, а в сторону границы среды, т.е. энергия волны не высвечивается в пространство, а лишь частично поглощается средой. При этом поле волны не возрастает при удалении от границы, как у вытекающей волны [4,10,11,16], а экспоненциально спадает, как у поверхностной волны. Причем это происходит и когда фазовая скорость волны меньше скорости света, и когда – больше. Таким образом, для того чтобы рассматриваемая волна была поверхностной, не требуется, чтобы ее фазовая скорость была медленнее чем у плоских волн над границей среды.

Версия 2. Также известно, что групповая скорость физической волны, переносящей энергию, не может быть больше скорости света с [4, 9-11]. Однако это утверждение верно только в том случае, когда групповая скорость оказывается равной энергетической скорости волны, т.е. скорости переноса волной энергии [4,17,18]. Выше же было показано, что рассматриваемые поверхностные волны к таким волнам не относятся. Их групповая скорость не равна энергетической скорости, которая меньше скорости света. Здесь нет нарушения закона ограничения скорости переноса энергии скоростью света с. При этом остаётся открытым вопрос о физическом смысле групповой скорости рассматриваемых волн. В [13,15] отмечено, что для волн с сильной аномальной дисперсией, что здесь как раз имеет место, групповая скорость может оказаться больше с, но это означает, что в этом случае она не имеет обычно придаваемого ей физического смысла, что, по-видимому, связано с ранее указанной спецификой волн, направляемых некоторыми волноведущими структурами.

Версия 3. Версия в свое время была опубликована одной из первых (см. дискуссию в [1] между двумя известными физиками Г.М.Барлоу и Дж.Р.Уэйтом). Эта версия связана с представлением полного поля, возбужденного источником над плоской границей электропроводящей среды, в виде интегрального разложения Вейля по «плоским волнам», а точнее разложения Фурье по продольным волновым числам [16,19,20]. При вычислении асимптотического выражения для возбужденного источником поля в дальней зоне методом перевала оказалось, что при переходе в комплексной плоскости волновых чисел к перевальному контуру интегрирования медленная поверхностная волна (фазовая скорость меньше с) выделяется из интеграла в качестве вычета, а быстрая волна (фазовая скорость больше с) не выделяется, что, казалось бы, можно интерпретировать как отсутствие поля такой волны в возбужденном источником поле. Но на самом деле указанная процедура дает количественную оценку только для алгебраической части асимптотической функции, разлагаемой по отрицательным степеням относительного (по отношению к длине волны) расстояния от источника и описывающей пространственное поле над направляющей границей. Экспоненциально же спадающее поле поверхностной волны как быстрой, так и медленной этой асимптотикой не описывается, поскольку спадающая экспонента в асимптотике фактически отсутствует: ее значение меньше значения любой как угодно высокой отрицательной степени расстояния от источника. Поэтому выделение или не- выделение в асимптотике из интегрального представления фактически нулевого поля поверхностной волны, медленной или быстрой, не играет роли, т.е. не является существенным. Причем сказанное справедливо (и это здесь важно при условии (3) ) и в случае расположения полюса, соответствующего поверхностной волне, вблизи точки перевала [19].

Как следует из другого, не асимптотического, способа представления полного поля источника в виде спектрального разложения по собственным волнам (по поперечным волновым числам с дискретно-непрерывным спектром) открытой направляющей структуры, здесь границы среды [16,20,21], такое разложение в исходном виде содержит кроме интеграла выделенную поверхностную волну независимо от того медленная она или быстрая [2]. Это разложение может быть получено как непосредственно на основании теории сингулярной (в бесконечном интервале) поперечной граничной задачи на собственные числа и собственные функции [16,21], так и путем преобразования указанного интегрального разложения Фурье по продольным волновым числам в разложение по поперечным волновым числам. Во втором случае при деформации контура интегрирования в комплексной плоскости волновых чисел этот контур одинаково заметает полюса подынтегрального выражения, соответствующие как медленной , так и быстрой поверхностным волнам [2,16,20]. Таким образом, поверхностная волна как медленная, так и быстрая содержится в полном поле, возбужденном источником, но она затухает и исчезает в асимптотике, где остается только поле пространственной волны.

Заключение

Рассмотренные волны представляют собой особый тип поверхностных волн, поверхностный характер которых, т.е. экспоненциальный спад поля от границы рассматриваемой высоко проводящей среды в поперечном направлении, имеет здесь место не по причине замедленности ее фазовой скорости относительно скорости плоских волн над границей среды, что оказалось здесь необязательным, а по причине частичного поглощения в ней энергии в процессе распространения волны. Представленные результаты показывают, что рассмотренная модель таких поверхностных волн, не противоречит физическим законам. Поэтому нет оснований сомневаться в том, что она описывает физические волны и когда их фазовая скорость меньше c, и когда – больше, а общепринятая «групповая» скорость для них, судя по всему, не имеет четкого физического смысла.

При этом, однако, такие волны имеют существенные недостатки с точки зрения использования их в технических приложениях. Во-первых, они слабо прижаты к границе среды, т.е. их поле имеет достаточно большую протяженность в поперечном направлении над границей, поэтому для их эффективного возбуждения может потребоваться источник со слишком большим размером вертикальной апертуры [16]. Во-вторых, их фазовая скорость лишь слегка отличается от скорости света с, поэтому любые, даже малые нерегулярности в плоскости границы среды могут привести к рассеянию поля волны и существенному увеличению потерь энергии при распространении вдоль границы. В частности такое может возникнуть при отклонении границы от плоскости, т.е. при наличии кривизны ее поверхности. Анализ рассмотренных поверхностных волн на нерегулярной границе требует специального исследования [16,22].

С другой стороны, при попытках применить поверхностные волны, например, на границах металлов в технических приложениях необходимо учесть, что поверхности реальных металлов обычно покрыты оксидными плёнками, имеющими толщину порядка долей микрона, микрона или нескольких микрон (естественные плёнки) и порядка десятков микрон (искусственно создаваемые плёнки для механической защиты поверхности металлов). В таком случае необходимо использовать результаты несколько иной теоретической модели направляющей системы: слоистой структуры типа металлическая подложка – диэлектрическая плёнка (обязательно с учётом потерь энергии в них) – свободное пространство [10]. Наличие пленки может существенно повлиять на прижатие поверхностной волны в сторону его увеличения и, следовательно, на возможность упрощения возбуждения волны и большую ее устойчивость по отношению к нерегулярностям структуры.

Автор данной статьи выражает благодарность Г.Г.Грачеву за помощь при подготовке статьи к публикации.

В качестве послесловия к статье отметим, что в сентябре 2012 года данная статья была представлена в журнал УФН, в котором перед этим была опубликована серия статей [5-9] , посвященных волне Ценнека, и, по существу, возникла дискуссия на эту тему. Однако статья не была принята для публикации по причине того, что редколлегия УФН решила «новые работы по волнам Ценнека к рассмотрению не принимать». В результате этого указанная публикация в УФН статей по данной теме фактически завершилась публикацией ошибочной статьи [9].

Литература

1. Barlow H. M., Wait J. R. // Electron. Letters. 1967.Т.3. №9.С.396.

2. Шевченко В. В. // Радиотехника и электроника. 1969.Т.14. №10.С.1768.

3. Oliner A. A. // IEEE Trans. MTT. 1984.T.32.№5.С. 1022.

4. Вайнштейн Л. А. Электромагнитные волны, 2-е изд. М.: Радио и связь, 1988.

5. Байбаков В. И.,Дацко В. Н.,Кистович Ю.В.//УФН.1989.Т.157.№6.С.722.

6. Кукушкин А. В. // УФН. 1993.Т.163. №1.С. 81.

7. Дацко В. Н., Копылов А. А. // УФН. 2008.Т.178. №1.С.109.

8. Кукушкин А. В. // УФН. 2009.Т.179. №7.С. 801.

9. Кукушкин А.В.,РухадзеА.А.,РухадзеК.З.//УФН.2012.Т.182.№11.С.1205.

10. Collin R. E. Field theory of guided waves, 2-nd ed. NY: IEEE Press, 1991.

11. Felsen L. B., Marcuvitz N. Radiation and Scattering of Waves. Englewood Cliffs, N.J.: Prentice-Hall, 1973 (Фелсен Л., Маркувиц Н. Излучение и рассеяние волн, т.2. М.: Мир, 1978).

12. Альперт Я. Л., Гинзбург В. Л., Фейнберг Е. Л. Распространение радиоволн. М.: ГИТТЛ, 1953.

13. Виноградова М. Б., Руденко О. В., Сухоруков А. П. Теория волн. М.: Наука, 1979.

14. Либенсон М. Н. Физическая энциклопедия. Т.3. М.: БРЭ, 1992. С.110.

15. Семенов Н. А. Техническая электродинамика. М.: Связь, 1973.

16. Шевченко В. В. Плавные переходы в открытых волноводах. М.: Наука, 1969 (Shevchenko V. V. Continuous Transitions in Open Waveguides. Boulder, Colo.: Golem Press, 1971).

17. Мандельштам Л. И. Лекции по оптике, теории относительности и квантовой механике. М.: Наука, 1972. С.420,431.

18. Зильберглейт А. С., Копилевич Ю. И. // Письма в ЖТФ. 1979.Т.5.№ 8. С. 454 .

19. Бреховских Л. М. Волны в слоистых средах. М.: Изд. АН СССР, 1957.

20. Barlow H. M., Brown J. Radio Surface waves. Oxf.: Clarendon Press, 1962.

21. Шевченко В. В.//Дифференциальные уравнения.1979.Т.15. №11.С.2004 (ShevchenkoV.V.//Differential Equations.1980.V.15. №11.P.1431).

22. Шевченко В. В. // Изв. ВУЗов – Радиофизика. 1971.Т.14. №5.С.768.