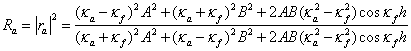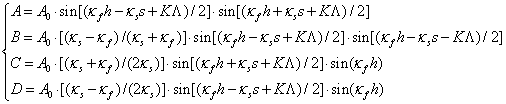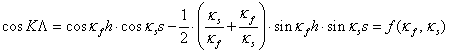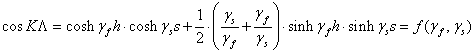"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 7, 2014

оглавление

УДК 535.075.8

МЕТОДИКА ИЗМЕРЕНИЯ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ ПРОЗРАЧНЫХ ДИЭЛЕКТРИЧЕСКИХ СРЕД

 

Д. Х. Нурлигареев 1,2, А. С. Беланов 1, М. В. Фадин 1,2

1 Московский государственный университет приборостроения и информатики

2 Научный центр лазерных материалов и технологий, Институт общей физики Российской академии наук

Статья получена 30 июня 2014 г.

Аннотация. Предложена методика измерения показателя преломления прозрачных диэлектрических сред, основанная на строгом аналитическом описании отражения оптического излучения на плоской границе однородного диэлектрика и одномерного фотонного кристалла (многослойной плёночной структуры).

Ключевые слова: одномерный фотонный кристалл, многослойная плёночная структура, волна Флоке-Блоха.

Abstract. The method of refractive index of transparent dielectric media measuring is proposed based on rigorous analytic description of optical radiation reflection on the plane boundary of homogeneous dielectric and one-dimensional photonic crystal (multi-layer film structure).

Key words: one-dimensional photonic crystal, multi-layer film structure, Floquet-Bloch wave.

 

1. Введение

Фотонные кристаллы широко исследуются с конца 1980-х годов, когда было осознано, что одно из их свойств – существование запрещённых зон в электромагнитных характеристиках, –  является чрезвычайно ценным с точки зрения многочисленных практических приложений [1]. Наиболее просто изготавливать одномерные структуры. Актуальным является изучение оптических структур, содержащих десятки и сотни слоёв [2]. Распространение света в таких структурах удобно представлять в форме волн Флоке-Блоха [3]. В частности, использование представления волны Флоке-Блоха в форме неоднородной волны позволило нам найти функцию коэффициента отражения плоской волны на границе полубесконечного [4-6] и ограниченного [7] одномерного фотонного кристалла. Найденные функции коэффициентов отражения и пропускания для ограниченного одномерного фотонного кристалла были с успехом применены для описания многослойного оптического фильтра [8], а также для определения структурных параметров ячейки фотонного кристалла посредством моделирования его измеренных угловых спектров отражения [9].

Целью данной работы является изучение возможности применения развитого описания для разработки методики измерения показателя преломления однородной диэлектрической среды, прозрачной в оптическом диапазоне длин волн. Суть предлагаемой методики заключается в применении строгих решений волнового уравнения для моделирования угловых спектров отражения на плоской границе фотонного кристалла с известными параметрами его ячейки и однородной диэлектрической среды при вариации её показателя преломления.

 

2. Брэгговские резонансы отражения и зонная структура одномерного фотонного кристалла

В случае полубесконечного фотонного кристалла c профилем показателя преломления n(x)

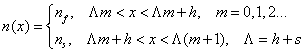                                             (1)

 

энергетический коэффициент отражения  (по интенсивности) ТЕ-поляризованной плоской волны, падающей наклонно ( - угол падения) из однородной среды с показателем преломления , определяемый как квадрат модуля амплитудного коэффициента отражения , равен [4, 5]

 ,                        (2)

где  - амплитудные коэффициенты определяются через параметры  ячейки кристалла и поперечные составляющие ,  (,  - длина волны в вакууме,  – продольная константа распространения) волновых векторов парциальных плоских волн в слоях ячейки (см. ф-лы (4) в [9]).

              (3)

В (3) при   действительные и блоховское волновое число K с точностью до  (где  - произвольное целое число) находится из уравнения

                          (4)

 

В случае  величина  в слоях с показателем преломления  действительная, а величина  в слоях с показателем преломления  становится мнимой, и поле в этих слоях представляется как результат интерференции экспоненциально затухающих волн. При этом

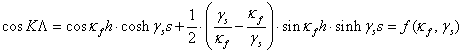   .                  (5)

 

Наконец, при  ,  

           .           (6)

 

Ранее нами было показано, что в случае наклонного падения плоской волны из однородной среды с показателем преломления  на полубесконечный фотонный кристалл в нём возбуждается волна Флоке-Блоха, а в однородной среде возникает отражённая плоская волна [4, 5]. При этом особенности углового спектра отражения связаны с особенностями зонной структуры одномерного фотонного кристалла.

Заметим, что при фиксированных  величины  в (4-6) являются функциями всего одной переменной - : , , ,  (здесь  - угол скольжения, связанный с углом падения ), и, следовательно, величины  в (3) могут быть представлены как функции . С учётом этого, величина  в (2) может рассматриваться как функция угла , в которую показатель преломления  входит в качестве параметра.

На рис.1 приведен график функции  в зависимости от  при мкм-1 и  для фотонного кристалла с параметрами ячейки:    мкм, аналогичными параметрам структуры, которая исследовалась нами ранее [3].

Значениям  удовлетворяющим неравенствам  и , отвечают, соответственно, фотонные запрещённые и разрешённые зоны.

Случай ,  (он реализуется в области малых углов скольжения , при выполнении условия ) ранее нами не рассматривался, остановимся на нём более подробно. В соответствии с (6) при всех возможных действительных значениях  , величина  оказывается мнимой (, ), и мы имеем дело с первой запрещённой зоной (нулевого порядка) фотонного кристалла и затухающей волной Флоке-Блоха. В данном случае, плоская волна, падающая из однородной среды на полубесконечный фотонный кристалл, должна испытывать полное отражение.

 

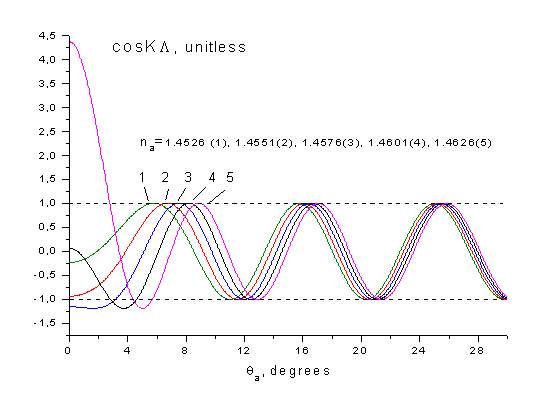
Рис.1. Графический метод определения зонной структуры одномерного фотонного кристалла

 

Пусть при значениях  равных  минус и плюс обозначают левый и правый края запрещённой зоны порядка ,  - максимальный возможный в данном кристалле порядок запрещённой зоны), выполняется условие . Тогда значениям , удовлетворяющим неравенствам , отвечают фотонные запрещённые зоны и затухающие волны. Между фотонными запрещёнными зонами расположены разрешённые зоны, для которых характерны распространяющиеся без затухания волны Флоке-Блоха. Расчёты показывают, что в данной структуре полному спектру возможных значений  (при вариации угла скольжения  в пределах от 0 до 900) соответствует 14 запрещённых и 14 разрешённых зон. Например, кривая (5) на рисунке представляет первые семь запрещённых и разрешённых зон, при вариации угла скольжения  в пределах от 0 до 300. Как видно, значениям  отвечает первая запрещённая зона , для неё , причём на левом краю (при ) этой зоны величина  максимальна, а на правом краю зоны (при ) . Для остальных запрещённых зон  на краях зон при = (), а внутри зон при ), когда выполняется условие , достигаются локальные максимумы . Каждое значение  () определяет центр соответствующей запрещённой зоны. Согласно с (2), в пределах запрещённых зон , и величина  фактически определяет угловую позицию брэгговского резонанса отражения порядка  на границе фотонного кристалла.

Следует заметить, что при изменении величины показателя преломления  величина резонансных значений  может изменяться. Согласно расчётам, уменьшение величины  должно приводить к уменьшению величины . В частности, при значениях  (кривые 1-4 на рисунке) резонанс 0-го порядка не реализуется. На рис. 2 показаны рассчитанные для рассматриваемой здесь структуры величины  при в зависимости от .

 

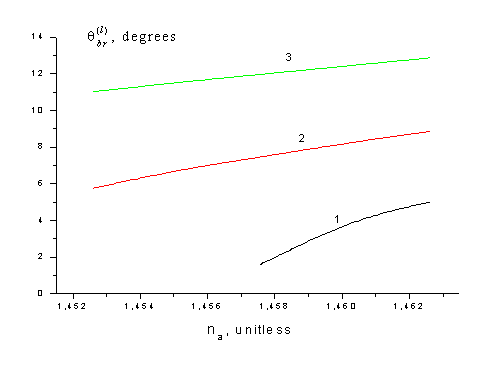
Рис.2. Величина  в зависимости от  при

 

Видно, что изменение (в пределах от  до ) величины  на  должно приводить к смещению позиции  на 2.75, 1.29 и 0.730 для брэгговских резонансов 1-го, 2-го и 3-го порядков, соответственно. В данном случае наиболее чувствителен к вариации величины  резонанс 1-го порядка.

 

3. Угловой спектр отражения ограниченного одномерного фотонного кристалла

Для фотонного кристалла, состоящего из  ячеек, обрамлённого двумя однородными средами с показателями преломления  и , коэффициент отражения  плоской волны, падающей наклонно из однородной среды с показателем преломления , равен в случае действительных  [7]

                                            (7)

 

где  и  - коэффициенты отражения плоской волны падающей на полубесконечный кристалл из среды с показателем преломления  и , соответственно,  - действительный параметр, определяемый как сумма фазовой задержки  при двойном проходе волны Флоке-Блоха через ограниченный фотонный кристалл и фазовых сдвигов, возникающих на его границах. В случае, комплексных  (где  - порядок запрещённой зоны) общие формулы для коэффициента отражения  имеют достаточно сложный вид [7]. В частности, в [7] показано, что при выполнении условия  - в брэгговских резонансах .

На рис.3 представлен коэффициент отражения , рассчитанный в зависимости от  для случая падения плоской волны из однородной среды с  на кристалл с параметрами ячейки , мкм и числом ячеек .

 

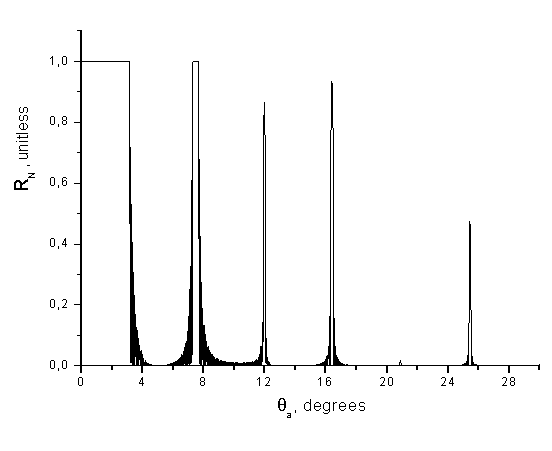
Рис.3. Зависимость  от  для плоской волны на границе одномерного фотонного кристалла при мкм,  мкм.

 

Из рис.3 видно, что при не при всех значениях , удовлетворяющих условию , когда блоховский волновой вектор возбуждаемой в периодической среде волны располагается внутри запрещённой зоны порядка l, может наблюдаться практически полное отражение падающей плоской волны. Очевидно, для структуры с конечным числом ячеек может существенно различаться не только относительная ширина, но и амплитуда брэгговских резонансов. Широкие резонансы легко регистрируются в эксперименте. Преимущество узких резонансов в том, что их угловые позиции могут быть установлены более точно. При значениях  расположенных вне запрещённых зон наблюдается лишь частичное отражение.

 

4. Техника эксперимента

          Для измерения распределения  была создана установка, принципиальная схема которой приведена на рис. 4. В ней используется призменный способ ввода излучения. Гауссов пучок He-Ne лазера с длиной волны  мкм вводится в исследуемый образец через торец, отполированный перпендикулярно грани, прижатой на оптический контакт с многослойной плёночной структурой, установленной на поворотном столике гониометра Г5М. Для снижения влияния паразитного отражения образец и структура располагаются в кювете с иммерсионной жидкостью. При этом величина  может быть найдена из измеренного угла падения  (в воздухе) лазерного пучка.

 

 

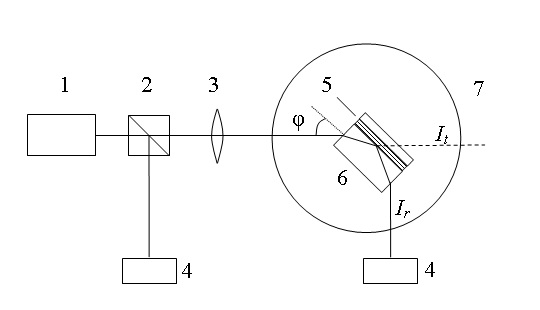
Рис.4. Схема измерения угловой зависимости коэффициента отражения светового пучка: 1 – He-Ne лазер, 2 –делитель пучка, 3 – длиннофокусная линза, 4 – фотоприёмник, 5 – образец с многослойной плёночной структурой, 6 – кювета с иммерсионной жидкостью, 7 – поворотный столик гониометра.

 

На рис. 5 представлен измеренный угловой спектр отражения для образца, погружённого в иммерсионную жидкость с показателем преломления . При размере сфокусированного пучка He-Ne лазера  мкм и угловой апертуре пучка (), зависимость измеренной величины  ( - интенсивность отражённого и падающего пучка) имеет сглаженный характер. Показаны шесть брэгговских резонансов отражения. Первый наиболее широкий резонанс отвечает второй запрещённой зоне (). Пятый резонанс подавлен. В данном случае ширина 2-го, 3-го и 4-го резонансов практически совпадает и определяется угловой расходимостью используемого пучка.

 

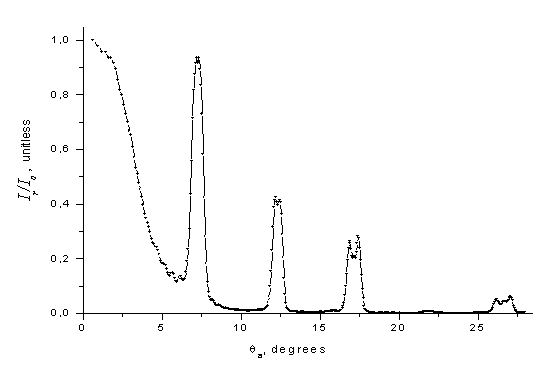
Рис.5. Измеренная зависимость величины  от величины  (, , мкм.)

 

Сопоставление полученных результатов с результатами моделирования, представленными на рис.2, показывает, что для определения величины  с погрешностью порядка  требуется регистрация сдвига брэгговских резонансов 1-го, 2-го и 3-го порядка с погрешностью, соответственно,  и . Для достижения более высокой точности желательно использовать в процессе измерений световые пучки с угловой расходимостью существенно меньше, чем 10.

 

5. Обсуждение результатов моделирования

Таким образом, моделирование показало, что резонансные значения , определяющие угловые позиции брэгговских резонансов отражения, определяются как структурными параметрами ячейки кристалла, так и показателем преломления  однородного диэлектрика, и, следовательно, при известных параметрах ячейки кристалла величина  показателя преломления диэлектрика может быть установлена из измеренного углового спектра отражения плоской волны на границе кристалла. Для повышения точности измерений желательно использовать широкие лазерные пучки с угловой расходимостью не превышающей угловую ширину резонансов отражения.

Отличительная особенность предложенного в данной работе метода состоит в возможности измерений позиций нескольких резонансов отражения, что позволяет существенно повысить точность получаемого результата. Кроме того, отметим возможность, после выполнения предварительного моделирования, изготовления фотонно-кристаллической структуры с оптическими характеристиками, наиболее чувствительными к вариациям показателя преломления (в выбранном диапазоне значений) исследуемой среды.

 

Литература

1.     E. Yablonovich. Inhibited spontaneous emission in solid state physics and electronics.// Phys. Rev. Lett.  58 (20), 2059-2062 (1987).

2.     И. Е. Голант, К. М., Голант, Новый метод расчета спектра и радиационных потерь вытекающих мод многослойных оптических волноводов. //ЖТФ. 76 (8), 99-106 (2006).

3.     Б. А. Усиевич, Д. Х. Нурлигареев, В. А. Сычугов, К. М. Голант. Возбуждение мод утечки в системе связанных волноводов.//Квантовая электроника. 37 (6), 580-583 (2007).

4.     Д. Х. Нурлигареев, В. А. Сычугов. Распространение света в одномерном фотонном кристалле: анализ методом функции Флоке-Блоха.//Квантовая электроника. 38 (5), 452-461 (2008).

5.     Д. Х. Нурлигареев. Распространение электромагнитной волны оптического диапазона в одномерном фотонном кристалле: анализ методом функции Флоке-Блоха.// Наукоёмкие технологии. 9 (7), 65-78 (2008).

6.     Д. Х. Нурлигареев. Волны Флоке-Блоха одномерного фотонного кристалла: общая теория. //Наукоёмкие технологии. 10, (9), 12-23 (2009).

7.     Д. Х. Нурлигареев. Волны Флоке-Блоха в ограниченном одномерном фотонном кристалле. //Поверхность. 2, 97-112 (2011).

8.     Д. Х. Нурлигареев. Применение метода функций Флоке-Блоха для описания многослойного оптического фильтра.//Инженерная физика. 11, 11-19 (2010).

9.     Д. Х. Нурлигареев, В. А. Сычугов. Методика определения параметров ячейки ограниченного одномерного фотонного кристалла, основанная на формализме функций Флоке-Блоха.//Краткие сообщения по физике ФИАН. 2, 3-10 (2012).