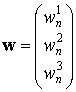УДК 621.396.132
ПАССИВНАЯ ЛОКАЦИЯ СО СВЕРХРАЗРЕШЕНИЕМ В АНТЕННОЙ РЕШЕТКЕ С ВЕКТОРНЫМИ АНТЕННЫМИ ЭЛЕМЕНТАМИ
С. Е. Мищенко1, В. В. Шацкий1, Н. В. Шацкий2
1ФГУП «Федеральный научно-производственный центр РНИИРС»
2Секция прикладных проблем при Президиуме РАН (Северо-Кавказское отделение), г. Ростов-на-Дону
Статья получена 2 июля 2014 г.
Аннотация. Разработан метод пространственно-поляризационного сверхразрешения на основе алгоритма типа Кейпона с использованием антенной решетки векторных антенн, обеспечивающий возможность построения пеленгационного рельефа с учетом поляризационных характеристик сигналов. Каждая из векторных антенн может осуществлять независимый приём трёх компонентов электромагнитного поля. Рассмотрен пример приёма пяти сигналов, действующих с различных направлений и имеющих различные поляризационные свойства.
Ключевые слова: алгоритм Кейпона, векторная диаграмма направленности, векторная антенна, пеленгационный рельеф, поляризационные свойства.
Abstract. The method is developed for spatial and polarization super-resolution based on Capon algorithm in the antenna array with vector antennas as its elements. Vector antennas provide the possibility of constructing direction-finding relief with account of polarization characteristics of the signals. Each vector antenna element consists of three orthogonal independent linear antennas. The example of five receiving signals acting from different directions and with different polarization properties is considered.
Key words: Capon algorithm, vector pattern, vector antenna, direction-finding relief, polarization properties.
Введение
Повышению эффективности пассивных радиолокационных комплексов с антенными решётками, связанному с пространственным разрешением принятых от целей сигналов, в настоящее время уделяется особое внимание. Все большее распространение цифровых антенных решеток (АР) приводит к расширению возможностей по обработке сигналов, применению различных методов пространственной обработки сигналов, в частности методов сверхразрешения. Методы сверхразрешения позволяют оценить пространственное положение и количество источников сигналов при разносе последних по угловым координатам, меньшем релеевского интервала разрешения [1-4]. При этом подразумевается, что все элементы АР имеют одну и ту же поляризацию. В то же время задача построения пеленгационного рельефа с учетом поляризационных характеристик сигналов в известной литературе практически не ставится. Между тем экспериментальные исследования [5] показывают, что селекция сигналов с учетом поляризационных характеристик позволяет повысить качество пеленгационного рельефа.
Цель работы состоит в разработке метода пространственно-поляризационного сверхразрешения на основе алгоритма типа Кейпона.
1 Модель антенной решетки с векторной диаграммой направленности
Пусть ![]() -элементная АР одновременно принимает группу
из
-элементная АР одновременно принимает группу
из ![]() сигналов. Каждый из сигналов
характеризуется направлением приема
сигналов. Каждый из сигналов
характеризуется направлением приема ![]() и компонентами
падающего поля
и компонентами
падающего поля ![]() , заданными в базисе источников
, заданными в базисе источников ![]() с ортами
с ортами ![]() .
.
Элементы АР имеют
несколько независимых входов, обеспечивающих прием сигналов в базисе наблюдения
![]() , заданного ортами
, заданного ортами ![]() .
.
Напряжение, наводимое на
каждом входе элемента АР ![]() -м сигналом, может быть
представлено в виде:
-м сигналом, может быть
представлено в виде:
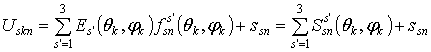 , (1)
, (1)
где ![]() −
составляющая шума в
−
составляющая шума в ![]() -м приемном канале;
-м приемном канале; ![]() − векторная ДН
− векторная ДН ![]() -го приемного канала в базисе наблюдения
-го приемного канала в базисе наблюдения ![]() при возбуждении поля единичной амплитуды
в базисе источников
при возбуждении поля единичной амплитуды
в базисе источников ![]() .
.
Выражение (1) позволяет
определить мощность ![]() -го сигнала в АР в виде квадратичной
формы:
-го сигнала в АР в виде квадратичной
формы:
![]() , (2)
, (2)
где символы «Т» и «*» обозначают
операцию транспонирования; ![]() − вектор-столбец
комплексных весовых коэффициентов, который может быть представлен в виде:
− вектор-столбец
комплексных весовых коэффициентов, который может быть представлен в виде:
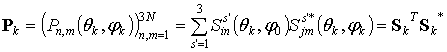 , (4)
, (4)
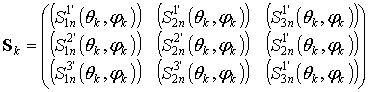 (5)
(5)
− прямоугольная блочная
матрица, каждый блок которой представляет собой вектор-строку из ![]() элементов, например:
элементов, например:
![]() . (6)
. (6)
Мощность шумов в ![]() -м канале АР представляет собой при
условии независимости тепловых шумов в каналах АР диагональную матрицу, ненулевые
элементы которой представляют собой мощность шума
-м канале АР представляет собой при
условии независимости тепловых шумов в каналах АР диагональную матрицу, ненулевые
элементы которой представляют собой мощность шума ![]() в
в ![]() -м канале при приеме
-м канале при приеме ![]() -составляющих сигнала в базисе наблюдения:
-составляющих сигнала в базисе наблюдения:
![]() ,
(7)
,
(7)
где 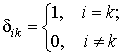 −
символ Кронекера.
−
символ Кронекера.
2 Алгоритм типа Кейпона для антенной решетки с векторной диаграммой направленности
В соответствии с [1] построение пеленгационного рельефа по алгоритму типа Кейпона строится с использованием выражения вида:
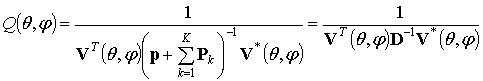 , (8)
, (8)
где ![]() −
вектор гипотеза, который имеет структуру, аналогичную (3); содержащий
комплексные весовые коэффициенты, обеспечивающие фазирование АР в направлении
−
вектор гипотеза, который имеет структуру, аналогичную (3); содержащий
комплексные весовые коэффициенты, обеспечивающие фазирование АР в направлении ![]() .
.
Существование обратной
матрицы ![]() определяется физическим смыслом эрмитовых
матриц
определяется физическим смыслом эрмитовых
матриц ![]() и
и ![]() .
.
Построение вектора гипотезы возможно в базисе источников и базисе наблюдения.
В первом случае будем иметь три вектора:
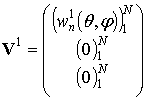 ;
;
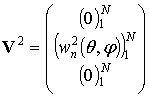 ;
;
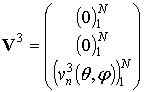 . (9)
. (9)
При переходе из базиса
наблюдения к базису источников с использованием матрицы ![]() :
:
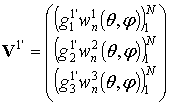 ;
;
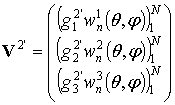 ;
;
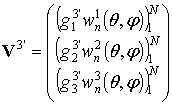 . (10)
. (10)
Если в качестве базиса
источников используется сферическая система координат, и орт ![]() ориентирован вдоль направления
распространения принимаемого сигнала, то в выражении (10) достаточно
использовать только два последних вектора. Например, для известной взаимосвязи
между декартовой и сферической системами координат в виде:
ориентирован вдоль направления
распространения принимаемого сигнала, то в выражении (10) достаточно
использовать только два последних вектора. Например, для известной взаимосвязи
между декартовой и сферической системами координат в виде:
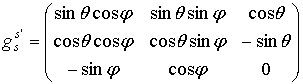 (11)
(11)
запишем:
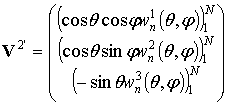 ;
;
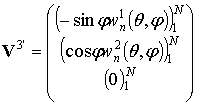 . (12)
. (12)
Таким образом,
предлагаемый метод построения пеленгационного рельефа отличается от известного
представлением матрицы ![]() . Размерность матрицы
. Размерность матрицы ![]() увеличивается в число раз, равное числу
входов элементов АР и соответствующим увеличением размерности вектора гипотезы,
число которых может быть связано либо с числом входов элемента АР (с числом
компонентов базиса наблюдения), либо с числом компонентов поля в базисе
источников (два вектора в случае использования сферической системы в качестве
базиса источников).
увеличивается в число раз, равное числу
входов элементов АР и соответствующим увеличением размерности вектора гипотезы,
число которых может быть связано либо с числом входов элемента АР (с числом
компонентов базиса наблюдения), либо с числом компонентов поля в базисе
источников (два вектора в случае использования сферической системы в качестве
базиса источников).
3 Результаты численных исследований
Рассмотрим линейную
64-элементную АР, состоящую из трех взаимно ортогональных тонких симметричных
вибраторов с совмещенными фазовыми центрами, каждый из которых образует векторную
антенну. Пусть векторные антенны размещены с шагом ![]() вдоль
орта
вдоль
орта ![]() декартовой системы координат. Геометрия
АР и ориентация ортов базисов источника и наблюдения приведены на рис. 1.
декартовой системы координат. Геометрия
АР и ориентация ортов базисов источника и наблюдения приведены на рис. 1.
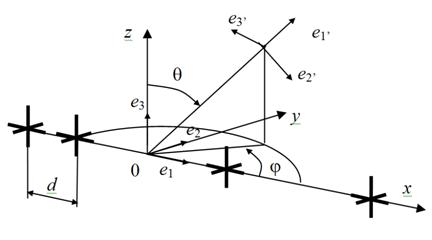
Рис. 1. Геометрия задачи
Базис наблюдения ![]() представляет собой декартову систему координат,
в котором объемные ДН вибраторов, ориентированных вдоль ортов
представляет собой декартову систему координат,
в котором объемные ДН вибраторов, ориентированных вдоль ортов ![]() , имеют вид:
, имеют вид:
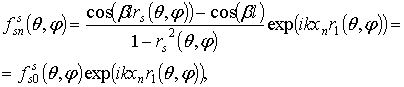 (13)
(13)
где ![]() −
длина плеча вибратора;
−
длина плеча вибратора; ![]() ;
; ![]() ;
; ![]() −
компоненты единичного вектора
−
компоненты единичного вектора ![]() ;
; ![]() − координата фазового центра
− координата фазового центра ![]() -го элемента.
-го элемента.
Считаем, что в зоне
наблюдения АР одновременно существуют ![]() сигналов,
действующих с направлений:
сигналов,
действующих с направлений: ![]() ;
; ![]() ;
; ![]() ,
, ![]() ,
, ![]()
![]()
![]() . Пусть
первый сигнал имеет две синфазные, равные по амплитуде составляющие поля в
базисе источников, второй сигнал является вертикально поляризованным, третий
сигнал − горизонтально поляризованным, а четвертый сигнал является сигналом
круговой поляризации. Будем считать, что амплитуды компонентов сигналов в базисе
источников одинаковы.
. Пусть
первый сигнал имеет две синфазные, равные по амплитуде составляющие поля в
базисе источников, второй сигнал является вертикально поляризованным, третий
сигнал − горизонтально поляризованным, а четвертый сигнал является сигналом
круговой поляризации. Будем считать, что амплитуды компонентов сигналов в базисе
источников одинаковы.
На рис. 2 приведены пеленгационные
рельефы, полученные в базисе источников. Из анализа результатов, представленных
на графике, следует, что первые два компонента обнаруживают по три сигнала,
причем каждый из компонентов обнаруживает сигналы, связанные только с
определенными поляризационными сигналами. Так, пеленгационный рельеф,
измеренный вдоль первого компонента базиса наблюдения, не содержит третий
сигнал (![]() ), а пеленгационный рельеф второй
составляющей базиса наблюдения − второй сигнал (
), а пеленгационный рельеф второй
составляющей базиса наблюдения − второй сигнал (![]() ).
Третий компонент также существует, но имеет очень маленький динамический
диапазон, что применительно к заданной помеховой обстановке не позволяет
использовать его для идентификации сигналов большинства сигналов, однако его
вклад будет возрастать при отклонении сигналов от направления нормали.
).
Третий компонент также существует, но имеет очень маленький динамический
диапазон, что применительно к заданной помеховой обстановке не позволяет
использовать его для идентификации сигналов большинства сигналов, однако его
вклад будет возрастать при отклонении сигналов от направления нормали.
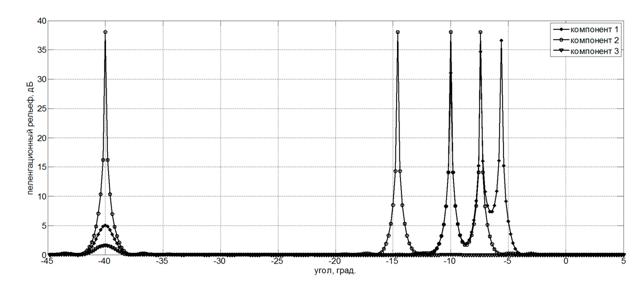
Рис. 2 − Пеленгационный рельеф в базисе источников
На рис. 3 приведены пеленгационные рельефы в базисе наблюдения.
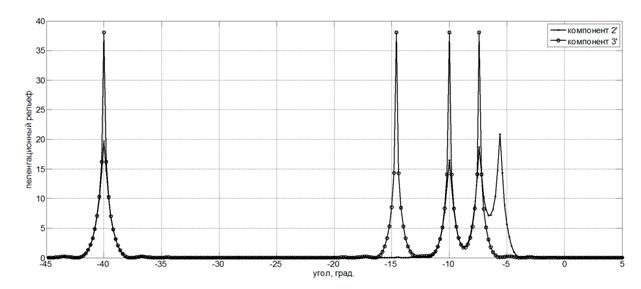
Рис. 3 − Пеленгационный рельеф в базисе наблюдения
Сопоставление результатов на рис. 2 и 3 показывает, что анализ пеленгационных рельефов в базисе источников в меньшей степени зависит от конфигурации входов элементов АР. Обращает на себя внимание изменение амплитуд пеленгов сигналов, измеренных для компонента поля 2’. Эти изменения зависят не только от углового расположения источника сигнала, но и от фазовых соотношений между компонентами поля в базисе наблюдения.
Необходимость различения сигнала отдельно по поляризационным составляющим демонстрирует рис. 4. На данном рисунке представлен пеленгационный рельеф, получаемый в случае, когда все элементы рассматриваемой АР имеют один общий вход.
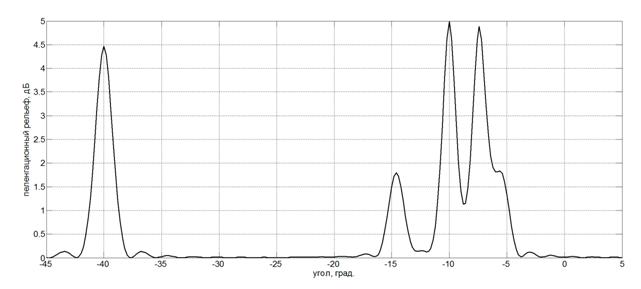
Рис. 4. Пеленгационный рельеф без учета поляризационных свойств сигналов
В результате антенные
элементы принимают все три составляющие поля в базисе наблюдения, однако,
возникающий в них ток представляет собой сумму высокочастотных токов в отдельных
вибраторах. В результате на рис. 4 наблюдается существенное уменьшение
динамического диапазона пеленгационного рельефа, ухудшение угловой разрешающей
способности, за счет расширения пеленгов и практически полная потеря второго
сигнала (![]() ) за счет наложения на его пеленг пеленга
первого сигнала (
) за счет наложения на его пеленг пеленга
первого сигнала (![]() ).
).
Заключение
Таким образом, предложенный метод демонстрирует возможность построения пеленгационных рельефов с помощью АР, антенные элементы которой имеют несколько независимо управляемых входов. Полезность такой процедуры для пассивной локации очевидна, она состоит в том, что в ряде случаев измерение одной составляющей принимаемого сигнала может оказаться недостаточным, что продемонстрировали результаты численных исследований. Полученные результаты показали, что при переходе к плоскому раскрыву амплитуды пеленгов будут зависеть не только от мощности сигнала, но и от их относительного расположения и поляризации.
Литература
1. Ратынский М. В. Адаптация и сверхразрешение в антенных решетках. М.: Радио и связь. 2003.
2. Спектральное оценивание / Тематический выпуск // ТИИЭР. 1982. Т. 70.
3. Пистолькорс А. А., Литвинов О. С. Введение в теорию адаптивных антенн. М.: Наука. 1991.
4. Габриэльян Д.Д., Лысенко А.В. Особенности формирования пеленгационного рельефа плоской антенной решеткой при использовании методов сверхразрешения. // Успехи современной радиоэлектроники. 2013. №8. С. 88 – 94.
5. Bongioanni C., Colone F., Martelli T., D'Angeli R., Lombardo P. Exploiting Polarimetric Diversity To Mitigate the Effect of Interferences in FM-Based Passive Radar // Proceedings og 11th International Radar Simposium (IRS-2010), Vilnius, Lithuania 16 - 18 June 2010, Vol. 1, pp.12-15.