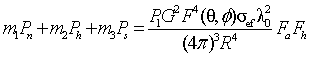УДК 621.396.67; 621.396.969
ПРОБЛЕМЫ РАДИОЛОКАЦИИ МОРСКИХ ЛЬДОВ С БУРОВЫХ ПЛАТФОРМ В АРКТИКЕ
А. И. Баскаков 1, М. В. Исаков 2, В. В. Егоров 3, А. М. Махалов 1, М. С. Михайлов 1, В. А. Пермяков 1
1 Национальный исследовательский университет МЭИ,
2 ОАО «НПК «Салют»», 3 Институт космических исследований РАН
Статья получена 7 июля 2014 г.
Аннотация. Проведен анализ распространения радиоволн в условиях Арктики и рассеяния их морской поверхностью и льдами в свете требований по разработке радиолокатора для мониторинга ледовой обстановки.
Ключевые слова: распространение радиоволн, Арктика, радиолокация льдин и айсбергов.
Abstract. In this paper, available data on propagation of radio waves in the Arctic region are analyzed and scattering of radio waves by the sea surface and ice is studied in the light of requirements for radar monitoring of ice.
Key words: propagation of radio waves, Arctic region, radars, monitoring of ice and icebergs.
Введение
Задача высокоточной оценки ледовой обстановки в районах морской добычи и транспортировки нефтегазовых ресурсов является актуальной для экономики России. В первую очередь речь идет об освоении нефтегазовых месторождений в Баренцевом море и в южной части Карского моря. В арктических морях часто бывают дожди, снегопады и туманы, которые чрезвычайно затрудняют условия добычи полезных ископаемых на шельфе и повышают опасность судоходства. Большую опасность при строительстве и эксплуатации сооружений могут представлять экстремальные скорости смещения кромки льда и внезапные вторжения морского льда в район расположения платформ.
Цель статьи – анализ состояния современных знаний по распространению радиоволн (РРВ) в условиях Арктики в свете требований по разработке радиолокатора для мониторинга ледовой обстановки. Рассмотрены следующие вопросы: особенности РРВ в условиях Арктики; особенности рассеяния радиоволн взволнованной морской поверхностью; разработка математических моделей рассеяния радиоволн морской поверхностью и ледовыми полями. Результаты обзора использованы при разработке предложений по созданию специализированного радиолокатора.
1. Особенности РРВ сантиметрового (СМ) и миллиметрового (ММ) диапазонов в Арктике
В условиях радиолокации льдов с платформ предполагаемая высота подъема радиолокатора составляет 25 -30 м, дальность работы – около 20 км. На РРВ СМ и ММ диапазонов влияют характеристики нижнего слоя тропосферы, примыкающего к поверхности моря. Основные физические механизмы распространения радиоволн в тропосфере: а) ослабление радиоволн, б) рассеяние радиоволн на осадках в обратном направлении, как помеха для РЛС, в) деполяризация радиоволн при рассеянии на осадках, г) рефракция радиоволн.
Ослабление электромагнитных волн. Теоретический анализ и экспериментальные исследования РРВ в тропосфере опираются на метеоданные для районов земного шара. Систематизированные результаты исследований РРВ изложены в рекомендациях Международного Союза Электросвязи (МСЭ) для расчетов ослабления радиоволн в молекулярной компоненте воздуха [4] и гидрометеорах [5-7], а также для учета влияния рефракции на РРВ [8-10]. Анализ рекомендаций МСЭ показывает, что в них отсутствуют данные по влиянию снега и смешанных (снег +дождь) осадков на РРВ при низких температурах воздуха. Необходимые для учета этих осадков данные имеются в [1,11–14]. В [14] изложены результаты экспериментов 2005 г. по ослаблению волн СМ диапазона на реальной трассе в Норвегии. Хотя значительная часть трассы шла над поверхностью земли, результаты эксперимента представляют интерес в связи с тем, что погодные условия по динамике близки к условиям в Баренцевом море. Что касается средних значений температуры, то они на данной трассе выше типичных для Баренцева моря значений. Согласно [14], наиболее вероятными являются потери (1% времени наблюдений ) от 2,5 до 7,5 дБ. Максимальные потери (10-3 % времени наблюдений) достигают величин 12 – 22 дБ. Наиболее надежный прогноз, разработанный на основе проведенных экспериментов, дает ослабление на трассе на 5-7 дБ больше по сравнению с прогнозом МСЭ для дождя при одинаковом проценте времени наблюдения этого ослабления.
Итоговые оценки суммарного ослабления СМ и ММ радиоволн в атмосфере для различных климатических условий в районе Баренцева моря приведены в таблице 1.
На основе данных таблицы 1 можно получить суммарное ослабление радиоволн в районе Баренцева моря при различных погодных условиях. Для более достоверной оценки ослабления необходимы надежные статистические данные о метеопараметрах в районе Баренцева моря. Для сравнения укажем, что согласно [11] осадки интенсивностью 10 мм/час наблюдаются на европейской территории России с вероятностью 0,13% , интенсивностью 30 мм/час – с вероятностью 0,04%.
Таблица 1. Затухание в
атмосфере, дБ/км в молекулярных компонентах воздуха и различных видах
гидрометеоров
в районе Баренцева моря при двукратном прохождении сигнала локатора по трассе
|
Частота
|
Сухой воздух Т= -5оС воды нет 1) |
Влажный воздух Т= 7оС, содержа ние воды 7,5 г/м3 1) |
Плотный туман Т=0оС, содержа ние воды 0,5 г/м3 2) |
Дождь интен- сивность 1 мм/час 3) |
Дождь интен- сивность 10 мм/час 3) |
Сухой снег Содержание воды эквивалентно дождю с интенсивностью 1 мм/час 4) |
Мокрый снег Содержание воды эквивалентно дождю с интенсивностью 1 мм/час 5) |
|
10 ГГц |
0,019 |
0,03 |
0,095 |
0,019 |
0,35 |
0,0019 |
0,038 |
|
35 ГГц |
0,064 |
0,21 |
1,1 |
0,5 |
4,6 |
0,05 |
1,0 |
Примечания к таблице 1 (номер примечания указан в конце первой строки каждого столбца): 1) расчет по рекомендации [3], 2) оценка по графику 1.1 рекомендации [7], 3) расчет по рекомендации [5], 4) оценка согласно [12], полученная путем уменьшения на порядок ослабления для дождя соответствующей интенсивности, 5) оценка согласно [12] и [14], полученная путем удвоения ослабления для дождя соответствующей интенсивности.
Рефракция радиоволн в тропосфере. Для расположения РЛС на высоте порядка 25–30 м наиболее важными характеристиками являются значения индекса преломления на уровне моря N0 и градиента индекса преломления на высоте ниже 65 м над уровнем моря [15]. Значение N0 в сухом воздухе в районе Баренцева моря колеблется в пределах от 310 (февраль) до 325 (август) [15]. Влияние водяного пара приводит к увеличению значения N0 приближенно на 25 N – единиц. Вероятности наблюдения градиентов индекса преломления в определенных границах были оценены в соответствии с [15] для четырех сезонов года. Вероятность наблюдения градиента индекса преломления величиной ≤-100 N–единиц/км составляет около 15% зимой, менее 1 % весной и летом, около 5 % осенью. Градиент индекса преломления в арктических морях отрицателен и 99% времени наблюдения его значения не превышают по модулю 30 N ед/км. При этом расстояние прямой видимости увеличивается примерно на 11%. С такой погрешностью эффектами рефракции можно пренебречь большую часть времени наблюдений.
Появление поверхностного волновода качественно меняет условия распространения радиоволн, поэтому важным аспектом прогноза распространения радиоволн является определение условий и вероятности возникновения волновода. Вероятность наблюдения поверхностного волновода в Арктике составляет менее 1% времени в течение года, а высота волновода – до 70 м [15] .Специфика формирования поверхностных волноводов в арктических льдах была изучена при выполнении специальной научно – исследовательской программы MIZEX (Marginal Ice Zone Experiment) [16,17]. Из проведенных экспериментов следует, что характеристики поверхностных волноводов резко различаются непосредственно над поверхностью льда и в открытом море [18,19]. Высота и модуль градиента индекса преломления волновода надо льдом значительно меньше, чем над морской поверхностью. Характеристики волновода меняются при переходе через границу лед – море. Эта особенность может сказаться на процессе отражения электромагнитного поля, идущего со стороны моря в поверхностном волноводе, от кромки льда.
Обратное
рассеяние электромагнитных волн осадками. Рассеянное
в обратном направлении на РЛС поле является помехой по отношению к информационному
сигналу, отраженному ото льда. Методика расчета рассеянного осадками поля
рассмотрена в [1,12]. Показано, что основной вклад в рассеянное назад поле
дает некогерентная компонента. Величина эффективной площади рассеяния (ЭПР)
осадков оценивается по приближенной формуле ![]() /2 , где
/2 , где ![]() - удельная ЭПР объема осадков, [1/м], a, b – линейные
размеры поперечного сечения главного лепестка диаграммы направленности антенны
на расстоянии R,
- удельная ЭПР объема осадков, [1/м], a, b – линейные
размеры поперечного сечения главного лепестка диаграммы направленности антенны
на расстоянии R, ![]() /2
- продольный линейный размер рассеивающего объема, определяемый длиной
импульса ti, с – скорость электромагнитной волны.
Предполагается, что R>> сti, а ослаблением поля в
пределах импульса можно пренебречь.
/2
- продольный линейный размер рассеивающего объема, определяемый длиной
импульса ti, с – скорость электромагнитной волны.
Предполагается, что R>> сti, а ослаблением поля в
пределах импульса можно пренебречь.
2. Особенности рассеяния СМ и ММ радиоволн взволнованной морской поверхностью
Сигнал,
отраженный от морской поверхности (МП), описывают в терминах удельной ЭПР
(УЭПР). Здесь УЭПР ![]() -
это ЭПР, приходящаяся на единицу площади поверхности S, т.е.
безразмерная величина
-
это ЭПР, приходящаяся на единицу площади поверхности S, т.е.
безразмерная величина ![]() .
В результате экспериментальных исследований выявлены определенные свойства
характеристик отражения радиоволн МП в зависимости от частоты и угла падения
волны. Они достаточно подробно описаны в ранних работах [12,20], которые не
потеряли своей ценности и к которым отсылается читатель. Зависимость УЭПР от
скорости и направления ветра над МП хорошо описывает следующая эмпирическая
формула [21, 22]
.
В результате экспериментальных исследований выявлены определенные свойства
характеристик отражения радиоволн МП в зависимости от частоты и угла падения
волны. Они достаточно подробно описаны в ранних работах [12,20], которые не
потеряли своей ценности и к которым отсылается читатель. Зависимость УЭПР от
скорости и направления ветра над МП хорошо описывает следующая эмпирическая
формула [21, 22]
![]() (1)
(1)
где ![]() - вид поляризации, причем первый индекс указывает поляризацию
излучаемых сигналов, а второй индекс – поляризацию принимаемых сигналов; Vв
– скорость ветра;
- вид поляризации, причем первый индекс указывает поляризацию
излучаемых сигналов, а второй индекс – поляризацию принимаемых сигналов; Vв
– скорость ветра; ![]() -
угол по отношению к направлению, противоположному вектору ветра (азимутальный
угол);
-
угол по отношению к направлению, противоположному вектору ветра (азимутальный
угол); ![]() и
и ![]() - константы, являющиеся
функциями угла падения радиоволн и поляризации. Значения констант выражения (1)
известны [21, 22]. Сравнение расчетных и экспериментальных зависимостей
значений УЭПР от скорости ветра [23] показывает хорошее их согласие. Измерения
проводились с помощью AAFE
RADSCAT для
горизонтальной поляризации (HH),
несущая частота 13,9 ГГц.
- константы, являющиеся
функциями угла падения радиоволн и поляризации. Значения констант выражения (1)
известны [21, 22]. Сравнение расчетных и экспериментальных зависимостей
значений УЭПР от скорости ветра [23] показывает хорошее их согласие. Измерения
проводились с помощью AAFE
RADSCAT для
горизонтальной поляризации (HH),
несущая частота 13,9 ГГц.
Существующие на сегодняшней день представления о рассеянии радиоволн поверхностью моря изложены в [12, 20, 24-26], см. также раздел 4.
3. Особенности рассеяния радиоволн СМ и ММ диапазонов ледовыми полями и кромками льдов
Особенности рассеяния
радиоволн ледовыми полями тесно связаны с процессами образования, развития и
разрушения морского льда. Ограниченные рамки статьи не позволяют детально
изложить этот вопрос. Отметим лишь, что в практическом отношении значительный
интерес представляет обнаружение айсбергов. Международная номенклатура морских
льдов определяет айсберг как обломок льда, выступающий над уровнем моря более,
чем на 5 м [13]. В северных широтах крупные айсберги имеют в поперечнике до 200
м и возвышаются над уровнем моря на 15…20 м. Для навигационной РЛС с ![]() см дальность
обнаружения
см дальность
обнаружения ![]() , как
функция высоты айсбергов
, как
функция высоты айсбергов ![]() выражается эмпирической формулой
[13]
выражается эмпирической формулой
[13] ![]() ,
где Rh - дальность радиогоризонта при нормальной рефракции;
,
где Rh - дальность радиогоризонта при нормальной рефракции; ![]() - высота айсберга в
метрах. Для айсбергов высотой 20…30 м дальность обнаружения составляет около
60% дальности обнаружения судов такой же высоты. Дальность обнаружения обломков
айсбергов с малой высотой падает до 20…25% и находится в пределах 10…30% от
радиогоризонта.
- высота айсберга в
метрах. Для айсбергов высотой 20…30 м дальность обнаружения составляет около
60% дальности обнаружения судов такой же высоты. Дальность обнаружения обломков
айсбергов с малой высотой падает до 20…25% и находится в пределах 10…30% от
радиогоризонта.
Электрические характеристики льдов и снега приведены в [24-26].
Особенности отражения ледовыми полями и кромками льдов на морской поверхности. Ледовые поля и кромки льдов представляют поверхностно – распределенную цель, занимающую область пространства, превосходящую по размерам элемент разрешения. Огибающая отраженного сигнала в этом случае оказывается растянутой во времени по сравнению с зондирующим, т.е. имеет место рассеяние по дальности. Если характеристики распределенной цели изменяются в течение времени накопления сигнала в РЛС, это приводит к расширению спектра отраженного сигнала. В этом случае говорят о рассеянии по двум параметрам – дальности и доплеровской частоте. Аналогично появляется рассеяние по углу в РЛС кругового обзора. Протяженные цели характеризуют следующими основными параметрами: средней ЭПР (усредненная по всем ракурсам); диаграммой вторичного рассеяния в азимутальной плоскости; законом распределения огибающей и спектром флуктуаций отраженного сигнала; соотношением геометрических размеров цели с протяженностью сигнала в пространстве и разрешающей способностью сигнала по дальности; соотношением геометрических размеров цели с высотой и длиной морских волн; временем пребывания цели в элементе разрешения РЛС.
Экспериментальные исследования характеристик обратного рассеяния СВЧ радиоволн морскими льдами и сравнение с расчетными зависимостями. Значительный объем экспериментальных исследований был проведен с помощью авиационных радиолокаторов бокового обзора (РБО) [3]. Результаты самолетных экспериментов, проведенных в различных районах Арктического бассейна, вполне удовлетворительно согласуются с данными наледных и вертолетных измерений [36], что свидетельствует об отсутствии региональных зависимостей в характере рассеяния радиоволн морскими льдами. И хотя данные самолетных исследований не могут быть полностью перенесены на интересующий нас случай скользящего падения, они полезны для формирования представлений о закономерностях рассеяния ЭМ волн СВЧ/КВЧ диапазонов различными видами льдов. Расчетные зависимости УЭПР хорошо согласуются с данными радиолокатора бокового обзора "Аналог" для диапазона частот 9-17 ГГц и углов падения 10о … 70о .
4 Математические модели рассеяния радиоволн морской поверхностью и ледовыми полями
Рассмотрим две основные модели. Модель 1 является комбинацией крупномасштабных пологих неровностей зондируемой поверхности и мелкомасштабных неровностей (по отношению к длине ЭМ волны). Эта модель пригодна для описания МП (с волнением до 2 баллов) и ледовых полей, кроме торосистых льдов и айсбергов. Модель 2 используется для описания поверхностей, имеющих разрывную, т.е. негладкую структуру (кромки льда, торосы, айсберги и т.п.), и обладает специфическими свойствами рассеяния, отличными от свойств предыдущей модели.
Зондирование МП и квазигладких льдов (модель1 ).
На основе теоретических и экспериментальных исследований харьковской школой [31-33] была разработана методика расчета УЭПР МП, в том числе и для настильных углов зондирования. Она описывает величину УЭПР с помощью трех аддитивных составляющих: составляющей, обусловленной рассеянием ЭМ волн на крупных и мелких неровностях, которая может быть названа фоновой компонентой, всплесках морских волн, а также компонентой, связанной с отражением волн от облака брызг и пенных образований. Авторами [31] было экспериментально показано, что при малых углах скольжения и волнении моря больше 2 баллов УЭПР всплесков морских волн для ММ и СМ диапазонов может превышать аналогичную величину фона (- 30 ÷ - 40 дБ) на десятки децибел. Вклад же брызговой компоненты еще более значителен и превышает УЭПР всплесков на 22 дБ на волне 8,6 мм и, соответственно, на 13 дБ на волне 3,2 см.
В работах [34,35] результаты исследований [31] были подтверждены и получили теоретическое развитие, что нашло свое отражение в виде следующей формулы для расчета УЭПР:
где ![]() - фоновая УЭПР морской поверхности (без всплесков и брызг);
- фоновая УЭПР морской поверхности (без всплесков и брызг); ![]() - оптическая толщина
облака брызг, равная γh,
γ
– погонное затухание в слое облака, h
– высота облака брызг;
- оптическая толщина
облака брызг, равная γh,
γ
– погонное затухание в слое облака, h
– высота облака брызг; ![]() -
радиолокационная отражаемость единицы объема облака.
-
радиолокационная отражаемость единицы объема облака.
При учете поляризации
сигнала на прием и передачу формулы расчета УЭПР - ![]() существенно усложняются [29]. Общая форма записи всех
компонент поляризационной матрицы УЭПР имеет следующий вид:
существенно усложняются [29]. Общая форма записи всех
компонент поляризационной матрицы УЭПР имеет следующий вид:
где верхние индексы при компонентах и
соответствующих слагаемых УЭПР, (указанные в скобках) означают их
принадлежность к типу модели поверхности, а нижние – к поляризации на
передачу-прием (V(В) – вертикальная, H(Г) – горизонтальная поляризации).
Выражения для слагаемых (3) из-за громоздкости не приводятся (см.[29]). Анализ
формулы (3) показывает, что зависимость величины УЭПР взволнованной МП от угла
визирования q и поляризации весьма существенна для
интерпретации данных радиолокационного зондирования, т.к. этот угол меняется в
них в достаточно широких пределах, вплоть до 900, т.е. включая
углы скольжения ![]() = 900 - q от 0 до 50
.
= 900 - q от 0 до 50
.
В модели 1 характеристики морских льдов входят в фоновую ЭПР. Данные о параметрах морских льдов использовались для расчета УЭПР однолетнего и многолетнего льдов, т.к. именно они представляют наибольшую угрозу безопасности морских буровых платформ. Результаты расчетов приведены в таблице 2.
Таблица 2 – Расчетные значения УЭПР (дБ) однолетнего и многолетнего морского льда для длин волн 8,6 мм и 3,2 см, как функции угла визирования θ.
|
Поляризация |
Однолетний лед |
|||||||
|
θ, град.(λ = 8,6 мм, εr = 2,92, εi = 0.003, σм = 0,0008 м, ρм = 0,0007 м, σк = 0,0085 м, ρк = 0,0875 м) |
||||||||
|
ГГ (HH) |
70,0 |
88,5 |
89,0 |
89,1 |
89,2 |
89,4 |
89,6 |
89,8 |
|
- 30,5 |
- 61,2 |
- 66,4 |
- 67,7 |
- 69,2 |
- 72,9 |
-78,2 |
- 87,2 |
|
|
ВВ (VV) |
- 20,0 |
- 45,0 |
-50,0 |
- 51,3 |
- 52,8 |
- 56,4 |
- 61,6 |
- 70,5 |
|
|
θ, град. (λ = 3,2 см, εr = 3,15, εi = 0,0015, σм = 0,003 м, ρм = 0,005 м, σк = 0,0085 м, ρк = 0,0875 м) |
|||||||
|
ГГ(HH) |
70,0 |
88,5 |
89,0 |
89,1 |
89,2 |
89,4 |
89,6 |
89,8 |
|
- 32,6 |
- 63,7 |
- 68,9 |
- 70,3 |
- 73,4 |
-75,5 |
- 81,6 |
- 89,7 |
|
|
ВВ(VV) |
- 15,6 |
- 41,0 |
- 46,0 |
- 47,3 |
- 48,8 |
- 52,4 |
- 57,8 |
- 66,5 |
|
|
Многолетний лед |
|||||||
|
θ, град.(λ = 8,6 мм, εr = 2,92, εi = 0,003, σм = 0,0008 м, ρм = 0,0007 м, σк = 0,0085 м, ρк = 0,0875 м) |
||||||||
|
70,0 |
88,5 |
89,0 |
89,1 |
89,2 |
89,4 |
89,6 |
89,8 |
|
|
ГГ(HH) |
- 30,5 |
- 61,1 |
- 66,3 |
- 67,7 |
69,2 |
- 72,9 |
- 78,1 |
- 87,1 |
|
ВВ(VV) |
- 19,7 |
- 45,0 |
- 50,0 |
- 51,3 |
- 52,8 |
-56,4 |
- 61,6 |
- 70,5 |
|
|
θ, град. (λ = 3,2 см, εr = 3,15, εi = 0,0015, σм = 0,003 м, ρм = 0,005 м, σк = 0.0085 м, ρк = 0.0875 м) |
|||||||
|
70,0 |
88,5 |
89,0 |
89,1 |
89,2 |
89,4 |
89,6 |
89,8 |
|
|
ГГ(HH) |
- 26,6 |
- 57,7 |
- 62,9 |
- 64,2 |
- 65,8 |
- 69,5 |
- 74,7 |
- 83,7 |
|
ВВ(VV) |
- 15,6 |
- 41,0 |
- 46,0 |
- 47,3 |
- 48,8 |
- 52,5 |
- 57,8 |
- 665 |
Анализ таблицы 2 показывает, что величина УЭПР как однолетнего, так и многолетнего льда сильно зависит от используемой поляризации зондирующего сигнала. Мощность эхо-сигнала при ВВ-поляризации на 12-17 дБ выше, чем соответствующие значения мощности при ГГ-поляризации. Диэлектрические характеристики льда слабо влияют на величину УЭПР. Основной вклад в рассеяние радиоволн вносит мелкомасштабная шероховатость льда. Малые значения УЭПР морского льда при малых углах скольжения (θ > 700) объясняются тем, что расчетные формулы модели 1 не учитывают рассеяние волн на передней кромке льдин, УЭПР которой, в этом случае, будет значительно превосходить, расчетные значения, приведенные в таблице 2. Эти расхождения наблюдаются уже при углах скольжения меньше 20о. Для углов визирования больше 88о (угол скольжения меньше 2о) основной вклад в рассеяние электромагнитных волн от ледовых полей и айсбергов будут вносить отражения от их передней кромки. Поэтому при оценке УЭПР квазигладких морских льдов, получаемой для настильных углов, необходимо к результатам расчетов по модели 1 добавлять значения УЭПР передней кромки льда. При малых и средних значениях угла визирования основной вклад в УЭПР будет давать модель 1. При настильных углах доминировать будет механизм рассеяния на передней кромке льда.
УЭПР передней кромки льда, торосистых льдов и айсбергов (модель2 ).
Указанные объекты имеют сложную геометрию, формируемую набором плоских граней большого, по сравнению с длиной волны ЭМВ, размера, а также поверхностями разрывного профиля. Вследствие сложности объектов разумно на основе экспериментального исследования рассеяния синтезировать модель отражения ЭМВ кромкой льда, торосистыми льдами и айсбергами.
Согласно
экспериментальным данным о мощности сигнала, отраженного айсбергами в диапазоне
3 см, ЭПР айсберга ![]() м2.
УЭПР льда лежит в пределах
м2.
УЭПР льда лежит в пределах ![]() =0,05…1,2 [13]. Большие значения
=0,05…1,2 [13]. Большие значения ![]() и
и ![]() получены для крупных айсбергов. Нижние границы значений ЭПР
близки к теоретической оценке. Значительное возрастание
получены для крупных айсбергов. Нижние границы значений ЭПР
близки к теоретической оценке. Значительное возрастание ![]() в ряде случаев можно
объяснить эффектом фокусировки отражений от различных блестящих точек крупных
айсбергов аналогично выбросам ЭПР от судов, а также наличием отвесных
поверхностей и участков, похожих на уголковые отражатели. Аналогичный эффект
дает отражение от «уголка», образуемого поверхностями айсберга. Учитывая, что
даже обломки айсбергов представляют собой значительную навигационную опасность
для буровой платформы (масса обломков составляет 100…150 т), для расчетов
дальности обнаружения и требований к энергопотенциалу РЛС рекомендуют значения
в ряде случаев можно
объяснить эффектом фокусировки отражений от различных блестящих точек крупных
айсбергов аналогично выбросам ЭПР от судов, а также наличием отвесных
поверхностей и участков, похожих на уголковые отражатели. Аналогичный эффект
дает отражение от «уголка», образуемого поверхностями айсберга. Учитывая, что
даже обломки айсбергов представляют собой значительную навигационную опасность
для буровой платформы (масса обломков составляет 100…150 т), для расчетов
дальности обнаружения и требований к энергопотенциалу РЛС рекомендуют значения ![]() м2 для
м2 для ![]() см [13].
см [13].
Основу используемого ниже эмпирического подхода составляют результаты экспериментов, описанных в [36-39]. В [36-39] утверждается, что преимущественный вклад в рассеяние радиоволн ледовыми объектами на море вносят отражения, формируемые площадью их поперечного сечения (рис.1). Электрофизические свойства льда, длина и поляризация падающей волны, поляризация эхо-сигнала оказывают слабое влияние на величину УЭПР объекта. Сама ЭПР объекта будет равна произведению УЭПР либо на площадь поперечного сечения, либо на площадь элемента разрешения радара. Согласно [36-39], УЭПР «разрывных» объектов слабо зависит от типа льда, длины волны зондирующего колебания и его поляризации и варьирует от 0,06 до 0,08, т.е. в пределах -11…-12,2 дБ. Отметим, что УЭПР плоской площадки льда с относительной диэлектрической проницаемостью εr=3, рассчитанная по энергетическому коэффициенту отражения плоской волны, равна 0,07, что согласуется с приведенными экспериментальными данными.
Подводя итоги, констатируем, что при расчете значений УЭПР может использоваться модель 1, учитывающая как влияние морской поверхности, так квазигладких морских льдов, и дополненная значениями УЭПР, относящимися к рассеянию радиоволн передней кромкой льда или миделем айсбергов. При настильных углах зондирования основной вклад в УЭПР вносит последний вид рассеивателей.
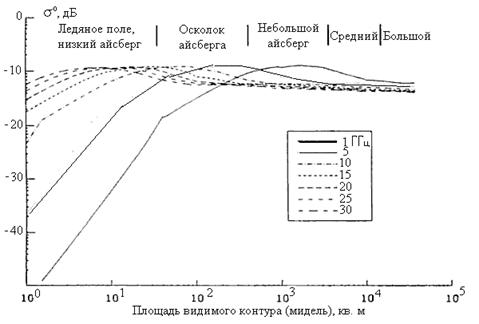
Рис. 1 – Модельные зависимости УЭПР льда и айсбергов от величины миделя [39].
5.Методики расчета энергетического потенциала РЛС в условиях локации морских льдов
Инженерная методика расчета энергетического потенциала РЛС
Для прогнозирования энергетического потенциала РЛС мониторинга ледовой обстановки с учетом влияния поглощения в атмосфере, гидрометеоров и морской поверхности была модифицирована методика расчета энергетического потенциала импульсных РЛС, изложенная в [12]. Согласно [12] учитываются потери в атмосфере и гидрометеорах, обратное рассеяние на гидрометеорах и морской поверхности. Модификация методики [12] заключается в следующем.
1) В случае малого морского волнения учтено зеркальное отражение электромагнитной волны от поверхности моря на больших дистанциях и переход от зеркального к случайному рассеянию по мере приближения к РЛС.
2) Сферичность морской поверхности учтена с помощью интерполяционной процедуры, предложенной в [40].
3) В случае сильного морского волнения учтено влияние рассеяния и потерь в брызгах и пене над морскими волнами по формуле (2).
4) Рефракция учтена в приближении эквивалентного радиуса Земли.
5) Используется сложный сигнал и когерентная обработка с накоплением отраженного сигнала. Поэтому уравнение радиолокации модифицировано с учетом процедуры обработки сложного сигнала.
С учетом всех перечисленных факторов максимальная дальность определяется из соотношения
В (4) P1 – мощность на входе
передающей антенны, G -коэффициент усиления антенны, F – амплитудная
ДН антенны, σef –ЭПР цели, λ0 – длина электромагнитной
волны, R – расстояние от РЛС до цели. т1 – коэффициент
различимости сигнала от цели на фоне шумов СВЧ части приемника, Рn–
мощность шумов приемника, Fа – множитель ослабления сигнала в
атмосфере, т2 – коэффициент различимости сигнала от цели на
фоне помех от гидрометеоров, Рh – мощность
сигнала, рассеянного гидрометеорами, Fh – множитель ослабления
в гидрометеорах, т3 – коэффициент различимости сигнала от
цели на фоне помех от морской поверхности, Рs –
мощность сигнала, рассеянного морской поверхностью, множитель ![]() в случае малого
волнения учитывает интерференцию поля, пришедшего прямо в направлении на цель,
и поля, отраженного от гладкой морской поверхности, множитель N – база
фазоманипулированного сигнала.
в случае малого
волнения учитывает интерференцию поля, пришедшего прямо в направлении на цель,
и поля, отраженного от гладкой морской поверхности, множитель N – база
фазоманипулированного сигнала.
Формула (4) переходит в
формулу для определения максимальной дальности, приведенную в [12] для простого
радиоимпульса, если положить в (4) N=1, а также пренебречь возможностью
зеркального отражения от морской поверхности, приняв ![]() =1.
=1.
Расчет ослабления сигнала в гидрометеорах проводился в соответствии с рекомендациями МСЭ [5], расчет сигнала, рассеянного гидрометеорами – по методике [12].
ЭПР взволнованной
морской поверхности рассчитывалась по заданным характеристикам главного
лепестка ДН и удельной ЭПР морской поверхности в соответствии с (2). Сведения о
значениях h, ![]() и γдБ для различных скоростей ветра
(V) и водности облака брызг (W) были взяты из [35]. По ним были рассчитаны
значения УЭПР взволнованной морской поверхности для λ = 8,6 мм и 3,2 см в
зависимости от скорости приповерхностного ветра.
и γдБ для различных скоростей ветра
(V) и водности облака брызг (W) были взяты из [35]. По ним были рассчитаны
значения УЭПР взволнованной морской поверхности для λ = 8,6 мм и 3,2 см в
зависимости от скорости приповерхностного ветра.
Фоновые значения УЭПР для длины волны 8,6 мм были приняты минус 50 дБ, для длины волны 3,2 см – минус 70 дБ. Для радиоволн с λ = 8,6 мм при среднем и сильном волнении моря УЭПР морской поверхности оценивается величиной от -2 до 1.1 дБ и будет выше, чем аналогичная величина для любого типа льда (от 10 до 12 дБ), т.е. контраст системы «вода-лед» всегда будет отрицательным. На длине волны 3,2 см УЭПР воды ниже, чем у ледовых объектов, на 5 ÷15 дБ, а контраст системы «вода-лед» - положительный (ЭПР льда выше ЭПР воды).
Помимо
рассеяния на морской поверхности, при малом волнении, когда поверхность можно
считать зеркальной, нужно учитывать переотражение от моря сигнала в направлении
цели и сопутствующее явление интерференции. Этот фактор учтен введением в
правую часть формулы (4) множителя ![]() , где интерференционный множитель Vi
равен
, где интерференционный множитель Vi
равен
В (5) h1, h2 - высоты подъема антенны РЛС и цели над поверхностью, коэффициент отражения ЭМ волны от морской поверхности по модулю равен единице, поверхность полагается плоской. Если приближение плоской поверхности неприменимо и следует учитывать сферичность земной поверхности, истинные высоты РЛС и цели в (5) заменяют приведенными высотами по формулам, данным в [40].
Интерференционная
формула (5) соответствует зеркальному отражению от гладкой поверхности. Как
известно, при скользящих углах падения θ=90о ‒ α
на неровную поверхность, ее можно считать гладкой при выполнении критерия Релея
![]() , где
, где ![]() - критическая высота
морских волн, выше которой нарушается критерий Релея,
- критическая высота
морских волн, выше которой нарушается критерий Релея,
![]() - текущая
высота морских волн.
- текущая
высота морских волн.
При высоте РЛС над морской поверхностью h1=25 м и расстоянии до цели от 1 км до 20 км угол скольжения α изменяется в пределах от 1,5о (0,025 рад) до 0,15о (0,0025 рад). Отсюда легко оценить высоту морских волн, при которой можно считать морскую поверхность гладкой. Таким образом, при выполнении критерия Релея в формулу (5) следует вводить интерференционный множитель, а в противоположном случае полагать его равным единице. Однако при таком подходе формула (5) приводит к разрыву в зависимости дальности от ЭПР цели. Для устранения этого разрыва предложена эвристическая аппроксимация интерференционного множителя, обеспечивающая отсутствие разрыва. Положим
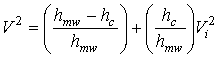 при
при 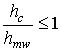 ,
, ![]() при
при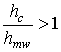 (6)
(6)
В (6) квадрат интерференционного множителя ![]() при невыполнении критерия
Релея заменяется эффективным множителем V2, равным сумме
двух слагаемых. Первое слагаемое учитывает вклад случайного рассеяния, второе –
вклад зеркального отражения. При этом вклад зеркального рассеяния считаем пропорциональным
отношению критической высоты морских волн к реальной высоте, а вклад случайного
рассеяния – относительному превышению реальной высоты морских волн над
критической.
при невыполнении критерия
Релея заменяется эффективным множителем V2, равным сумме
двух слагаемых. Первое слагаемое учитывает вклад случайного рассеяния, второе –
вклад зеркального отражения. При этом вклад зеркального рассеяния считаем пропорциональным
отношению критической высоты морских волн к реальной высоте, а вклад случайного
рассеяния – относительному превышению реальной высоты морских волн над
критической.
При учете высоты
морских волн полагалось также, что в расчетные формулы нужно подставлять не ЭПР
цели над гладкой морской поверхностью, а ЭПР, уменьшенную пропорционально
высоте цели над средней высотой морских волн ![]() .
.
Применение метода параболического уравнения к расчету энергетического потенциала РЛС.
Метод параболического уравнения (МПУ) является эффективным численным методом, позволяющим учесть нерегулярность морской поверхности, неоднородность тропосферы и малые потери в ней. Систематическое изложение МПУ дано в монографии [41], на базе МПУ разработаны программные комплексы для расчета распространения радиоволн и энергетического потенциала РЛС [42,43]. Известные реализации МПУ имеют область перекрытия с инженерной методикой, но не позволяют учесть эффекты обратного рассеяния электромагнитных волн на морской поверхности и гидрометеорах. В НИУ МЭИ разработана программа расчета энергетического потенциала РЛС по МПУ, сопоставимая по своим возможностям с программами [42,43].
Оценка УЭПР льдин и айсбергов
Обзор теоретических моделей рассеяния электромагнитных волн на льдах показал отсутствие методов расчета ЭПР краев льдин и айсбергов. В этой связи были проведены численные исследования УЭПР двумерной модели края льдин на основе метода поверхностных интегральных уравнений [44]. Численные результаты показали, что УЭПР края льдины сильно зависит от формы торцевой части льда, варьируясь в пределах от весьма малых значений порядка 0,01 до 13,5. Максимальные значения соответствуют идеально гладкой вертикальной стенке льдины, значения около 0,07 - стенке с мелкомасштабными неровностями. Таким образом, расчетный интервал колебаний УЭПР перекрывает диапазон наблюдаемых экспериментально величин УЭПР льдов и айсбергов [13, 36-39].
Оценка энергетического потенциала РЛС при работе по целям типа морского льда на основе инженерной методики
Оценим влияние совокупности различных факторов на энергетический потенциал РЛС. Для этого используем формулу (4), в которой приняты следующие исходные данные. Выбран летний сезон с параметрами тропосферы: давление 101,3кПа, температура +7 оС (290К), концентрация водяных паров 7,5 г/м3. Рассматривались случаи выпадения осадков в виде дождя интенсивностью 6 – 30 мм/час. Связь балльности волнения с высотой морских волн определялась по рекомендации Всемирной Метеорологической Организации, согласно которой под средней высотой понимается значительная высота морских волн (Significant Wave Heith H1/3). В расчетах средняя высота менялась от 0,1 м (балльность волнения – 1) до 4 м (балльность волнения – 6). Для последнего случая отдельно рассмотрены модели морской поверхности без брызг и с брызгами при ветре со скоростью 15 м/с. Значение тропосферной рефракции выбрано стандартным.
Параметры антенной системы: РЛС работает в двух диапазонах – 3,2см и 8 мм. Параметры главного лепестка ДН: для 3,2см - 1,5о в азимутальной плоскости, 3,5о в угломестной плоскости, коэффициент усиления G=38 дБ, для 8 мм: 0,4о в азимутальной плоскости, 1о в угломестной плоскости, коэффициент усиления G=49 дБ. Высота антенны РЛС над поверхностью моря 25м, высота цели варьируется. Импульсная мощность 10 Вт. Длительность дискрета в составе сигнала 6 мкс, база сигнала N=1023, длительность импульса приблизительно 6 мс. Мощность шумов на входе приемника ≈10-12 Вт, база сигнала N=1023. Вероятность правильного обнаружения цели задана равной 0,9, вероятность ложной тревоги – 10-2. На рис. 2 и 3 приведены для данного примера результаты расчетов зависимости максимальной дальности от ЭПР цели при различных погодных условиях.
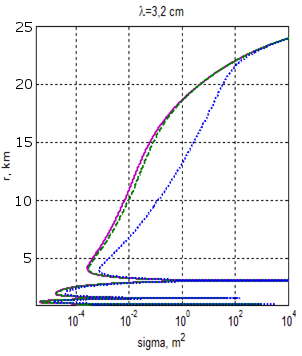
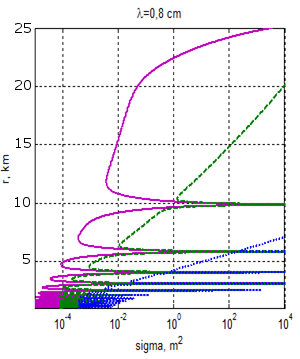
Рис.2. Зависимость дальности обнаружения цели от ЭПР цели для дождей различной интенсивности, при спокойном море (высота волны 0,1 м, балльность 1) и высоте цели – 2 м. Сплошная линия – отсутствие дождя, штриховая – дождь интенсивностью 6 мм/час, пунктирная – дождь интенсивностью 30 мм/час.
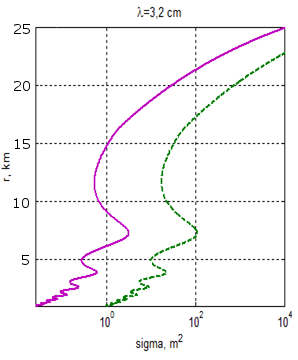
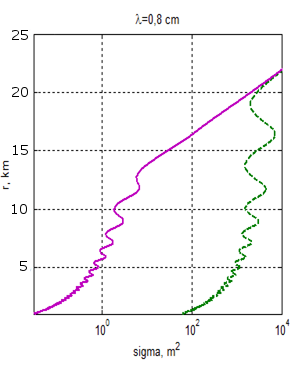
Рис.3. Зависимость максимальной дальности обнаружения цели от ЭПР цели при высоте цели 5м, высоте морских волн 4 м (6 баллов), с учетом брызг (штриховая линия) и без учета брызг (сплошная линия), при дожде интенсивностью 6 мм/ч.
Применимость инженерной методики ограничена освещенной зоной на расстояниях примерно меньше 0,8 от расстояния прямой видимости, на больших расстояниях следует учитывать явления дифракции. Ниже на рис. 4 приведено сравнение расчетов отношения сигнал/шум от дальности до цели по инженерной методике (штриховая линия) и по МПУ (сплошная линия) для цели с ЭПР 100 м2. Влияние морского волнения учитывалось в программе заданием реализации морской волны в виде синусоиды в отличие от известной программы [42], где использовалась статистическая модель морского волнения. В нашей модели профиль волны характеризуется двумя независимыми параметрами: высотой h и длиной Λ морской волны.
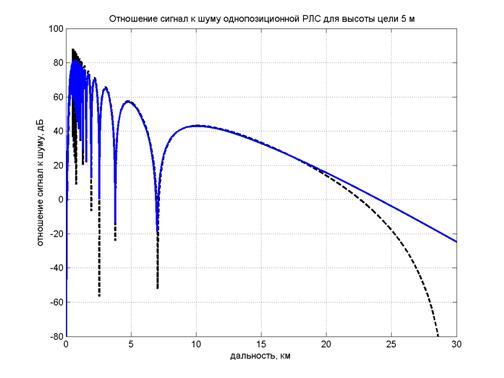
B=0
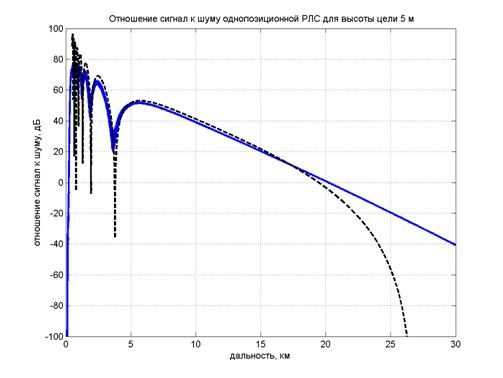
B=4
Рис. 4 Сравнение расчетов, выполненных по инженерной методике (черная штриховая линия) и по МПУ (сплошная синяя линия). Балльность равна нулю (вверху) и 4 балла (внизу), при этом высота морской волны принята равной 2,5 м, длина - 25 м. ЭПР цели 100 м2.
Как следует из сравнения результатов расчетов, инженерная методика согласуется с расчетом по МПУ до расстояний, близких к расстоянию прямой видимости, а далее дает заниженные уровни сигнала. Влияние морского волнения незначительно при балльностях менее 3-х, при дальнейшем увеличении балльности дальность действия РЛС заметно падает. При больших балльностях и h>0,1Λ данная модель волны теряет смысл.
Результаты анализа позволяют сделать следующие выводы.
1. В условиях стандартной атмосферы в отсутствие сильного морского волнения и осадков энергетического потенциала проектируемого радара, т.е. отношения энергии эхо-сигнала, приходящего от зондируемых объектов (ледяные поля, торосы и айсберги, наблюдаемые на фоне морской поверхности), к уровню шума приемника достаточно для решения задачи обнаружения объектов типа льдин и айсбергов на расстояниях, близких к радиогоризонту . При наличии интенсивных дождевых осадков (порядка 30 и более мм/ч) потенциал радара недостаточен для обнаружения целей типа льдов на дальностях, близких к радиогоризонту, однако вероятность выпадения таких осадков в северных районах весьма мала.
2. Волнение морской поверхности, характеризующееся обрушением волн и появлением облака брызг, приводит к снижению контраста ледяных объектов на фоне моря и ухудшению характеристик обнаружения и классификации типов льда.
3. УЭПР ледяных полей при возникновении интенсивных дождевых осадков (порядка десятков мм/ч) и густого тумана подвергается не слишком существенным изменениям по сравнению с влиянием облака брызг. Влияние облачности оказывается еще более слабым.
4. На основе расчетов, проведенных при учете кривизны морской поверхности и зеркального отражения от моря, можно сделать вывод, что энергетический потенциал предлагаемой РЛС в случае незначительного морского волнения (до 3-х баллов) и в отсутствие осадков обеспечивает обнаружение целей типа морского льда с ЭПР порядка 10 м2 на расстояниях 20-23 км, при больших ЭПР – до 25 км.
5. При наличии слабых осадков (до 6 мм/ч) по всей длине трассы дальность обнаружения цели с ЭПР порядка 10 м2 остается на уровне 20 км на длине волны 3,2 см и падает до 13 км на длине волны 0,8 см. Если учесть, однако, что вероятность существования дождей одновременно на всей трассе мала, то следует ожидать сохранения дальности обнаружения по целям указанного размера вплоть до осадков интенсивностью 30 мм/ч при горизонтальной протяженности дождя порядка 1 км.
6. Наихудшими являются условия обнаружения целей при сильном морском волнении, особенно в условиях обрушения волн, когда существенную роль начинает играть рассеяние и потери в брызгах. Для увеличения дальности действия РЛС по объектам типа льдин в этом случае целесообразно рассмотреть дополнительные возможности типа постпроцессорной обработки [45], позволяющие усилить контраст целей на фоне морского волнения.
Заключение
По результатам проведенного обзора были подготовлены предложения по созданию специализированного радиолокатора, предназначенного для установки на морских платформах, обнаружения ледовых полей, отдельных льдин, айсбергов и измерения их характеристик (размеры льдин, скорость движения льда, размеры торосов и т.д.) на расстояниях до 20-25 км. На основе разработанных технических предложений получен патент РФ [46].
Работа выполнена при частичной финансовой поддержке РФФИ (проект № 13-08-00735а) и РНФ (проект № 14-09-01208).
Литература
1. Красюк Н.П., Розенберг В.И. Корабельная радиолокация и метеорология. -Л.: Судостроение, 1970, 325 с.
2 Мельник Ю.А., Зубкович С.Г., Степаненко В.Д. Радиолокационные методы исследования Земли. // Под ред. Ю.М. Мельника. – М.,: Советское радио, 1980, 264 с
3 Калмыков А.И., Митник Л.М. Радиолокация поверхности Земли из космоса. – Ленинград, Гидрометеоиздат, 1990, 200с.
4 Рекомендация ITU-R P.676-5. Attenuation by atmospheric gases.
5 Рекомендация ITU-R P.838-1. Specific attenuation for rain for use in prediction methods.
6 Рекомендация ITU-R P-839-3. Rain height model for prediction methods.
7 Рекомендация ITU-R P-840-3. Attenuation due to cloud and fogs.
8 Рекомендация ITU-R P-369-6. Reference atmosphere for refraction.
9 Рекомендация ITU-R P-369-6. The radio refractive index: its formula and refractivity data.
10 Рекомендация ITU-R P-834-3. Effects of troposphere refraction on radio wave propagation.
11 Калинин А.И. Распространение радиоволн на трассах наземных и космических радиолиний. - М.: Связь, 1979, -296 с.
12 Красюк Н.П., Коблов В.П., Красюк В.Н. Влияние тропосферы и подстилающей поверхности на работу РЛС. –М.: Радио и связь. 1988. – 216 с.
13 Винокуров В.И., Генкин В.А., Калиниченко С.П. и др . Морская радиолокация /Под ред. д.т.н., профессора В.И. Винокурова, Ленинград. Судостроение, 1986, -256с.
14 Terje Tjelta, Lars Erliks Bråten, Tor Ore Breivik. Predicting the Attenuating Distribution on Line-of- Sight Radio Links due to melting Snow. / R&D No. 35/2005, Telenor.
15 Рекомендация ITU-R P-453-8. Radio refractive index: its formula and refractivity data.
16 Sechrist F.S., Fetty R.W., Perryman D.C. Forecasters Handbook for the Arctic. Naval Environmental Prediction Facility. Monterey, CA, Technical Report TR 89012, 1989.
17 MIZEX. A Program for Mesoscale Air-Ice-Ocean Interaction Experiments in Arctic Marginal Ice Zones.
18 Willis Z.S. The spatial and temporal variability of the atmospheric boundary layer and its effect on electromagnetic propagation. Master’s thesis. Naval postgraduate school, Monterey, CA, 1987.
19 Shaw a.o. Horizontal variability of mean refractivity structure in the Arctic. //Proc. Conference on Microwave Propagation in the Marina Boundary Layer. 1989
20 Справочник по радиолокации, Т. 1. / Под ред. М. Сколника, - М.: Сов. радио, 1976
21 Мур Р.К., Фэн А.К. Радиолокационные определения параметров ветра над морем. ТИИЭР, том 67, № 11, 1979, с.56
22 Michael W. Spencer, Chialin Wu and David G. Long. Improved Resolution Backscatter Measurements with the SeaWinds Pencil-Beam Scatterometer. / IEEE Transactions on geosciences and remote sensing, vol. 38, no. 1, January 2001
23 David G. Long and Michael W. Spencer. Radar Backscatter Measurement Accuracy for a Space borne Pencil-Beam Wind Scatterometer with Transmit Modulation. /IEEE Transactions on geosciences and remote sensing, vol. 35, no. 1, January 1997
24 Богородский В.В., Гаврило В.П. Лед, физические свойства, современные методы гляциологии. Л. Гидрометеоиздат, 1980, -384с.
25 Ramseier R. O., G1оersen P., Сampbe11 W. J., Chang Т. С. Mesoscale description for the principal Bering Sea ice experiment.— In: USSR/USA Bering Sea Experiment. Proc. Final Symp. on the Results Goint Soviet-American Expedition.—Rotterdam, 1982, p. 231—236
26 Ha11iкainen M. Т., U1abу F. Т., A1de1razik M. Dielectric properties of snow in the 3 to 37 GHz range.— IEEE Trans. Antennas Propag., 1986, v. 34, No. 11, p. 1320—1340
27 Kim Y. S., Moore R. К, Оnstо1l R. G., Gegineni S. Towards identification of optimum radar parameters for sea-ice monitoring.— J. Glaciol., 1985, v. 31, No. 109, p. 214—219
28 Радиолокационные методы и средства оперативного дистанционного зондирования Земли с аэрокосмических носителей./ Под ред. академика НАНУ, д.т.н. Конюхова С.Н., чл.-корр. НАНУ, д.т.н. Дронского В.И., к.т.н. Цымбала В.Н. Тр. Национальная академия наук Украины. Национальное космическое агентство Украины. Центр радиофизического зондирования Земли им. А.И. Калмыкова. Киев, 2007.
29 Жуковский А.П., Оноприенко Е.И., Чижов В.И. Теоретические основы радиовысотометрии. М., «Сов. Радио», 1979, 320 с.
30 Зубкович С.Г. Статистические характеристики радиосигналов, отраженных от земной поверхности. М., «Сов. Радио», 1968.
31 Калмыков А.И., Курекин А.С., Лемента Ю.А.и др. Особенности рассеяния СВЧ излучения на обрушивающихся морских волнах. / Изв. ВУЗов. Радиофизика, 1976, Т. 19, № 9, с. 1315 – 1321.
32 Басс Ф.Г. , Фукс И.М. Рассеяние волн на статистически неровной поверхности. М., «Наука», 1972.
33 Bass P.G, Braude S.Ya., Fuks I.M., Kalmykov A.I. et al. Radiophysical investigations of sea roughness (radiooceanography) at the Ukrainian Academy of Sciences. / IEEE Trans. on Antennas and Propag. , 1977, AP-25, № 1, pp. 43-52.
34 Спиродонов Ю.Г., Пичугин А.П. Влияние метеоусловий на характеристики радиолокационных изображений земной поверхности из космоса //Исслед. Земли из космоса, 1984. № 6. С. 21 -27.
35 Шарков Е.А. Обрушающиеся морские волны: структура, геометрия, электродинамика. М.: «Научный мир». 2009. 303 с.
36 Walsh J., Dawe B.J., and Srivastava S.K.. /IEEE J. Oceanic Eng., OE-11(2), 1986.PP. 276-284.
37 Ryan J. and Walsh J. Electric dipole fields over quarter space earth inhomogenity and application to ice hazard detection // Radio Sci., 20, 1985. PP. 1518-1528.
38 Rossiter J.R., Guidne J., Hill C.et al. Remote sensing detection capabilities – East coast. Env. Studies Res. Funds. April 1995. Report N 132.
39 Haykin S. S., Lewis E.O., Raney R.K., Rossister J.R.. Remote sensing of sea ice and icebergs. John Wiley & Sons Inc. 1994.687 pp.
40 Пермяков В.А., Солодухов В.В., Бодров В.В., Исаков М.В. Распространение радиоволн, -М.: Издательский дом МЭИ, 2008, -189 с.
41 Parabolic equation methods for electromagnetic waves propagation./M. Levy. –London, UK, IEE, 2000.
42 A. E. Barrios. Advanced Propagation Model (APM) Computer Software Configuration Item (CSCI) Documents./D. R. Sailors, A. E. Barrios, W. L. Patterson, H. V. Hitney // Technical document 3033, August 1998.
43 CARPET (Computer-Aided Radar Performance Evaluation Tool). [Электронный ресурс]. – Режим доступа к ресурсу: www/URL: http://www.tno.nl/downloads/carpet.pdf.
44 Комаров А.А, Пермяков В.А. Дифракция плоской электромагнитной волны на диэлектрической ступеньке. / Журнал Радиоэлектроники, июль 2013. http://jre.cplire.ru/jre/aug13/7/text.html
45 Ice Radar Processor for Prince William Sound – Summary of Configuration and Benefits. C-CORE Report R-07-044-546. V.3.0, December, 2007.
46 Баскаков А.И., Егоров В.В., Исаков М.В., Пермяков В.А., Лукашенко Ю.И. Способ обнаружения высокоточного определения параметров морских ледовых полей и радиолокационная система, его реализующая. // Патент на изобретение. Заявка № 2011113486 /07 (019983). Дата приоритета 08.04.2011. Дата выдачи 05.02.2012. Страна: Россия.