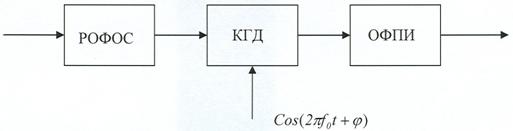
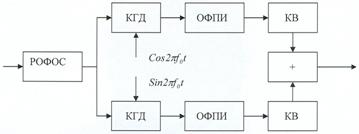
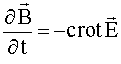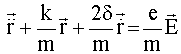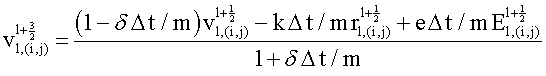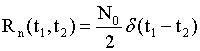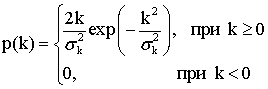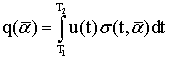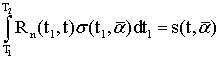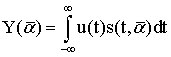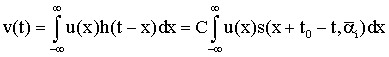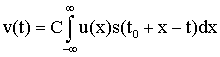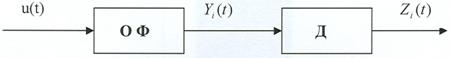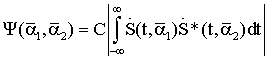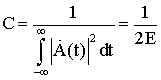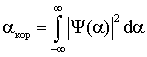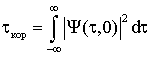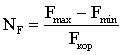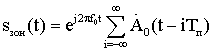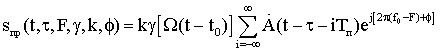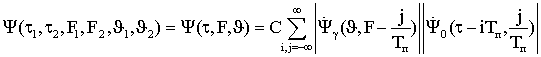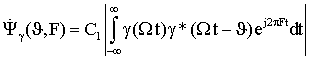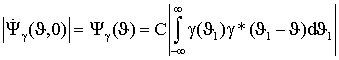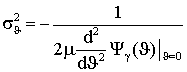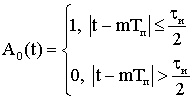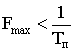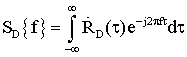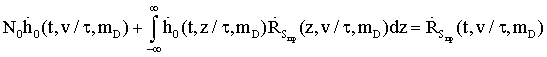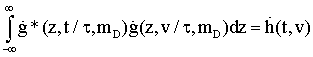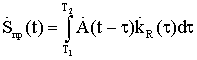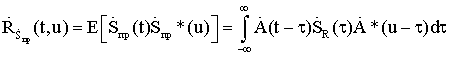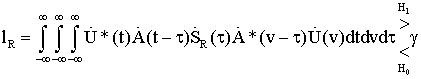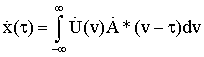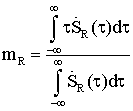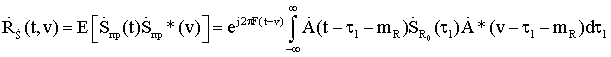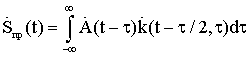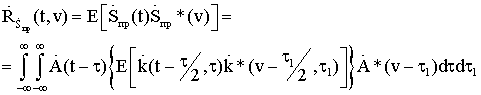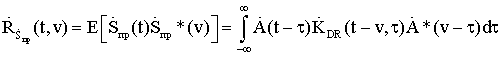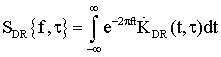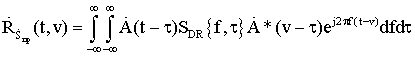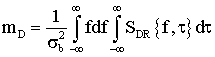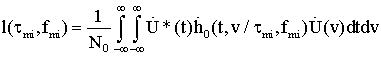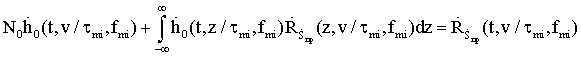УДК. 621.396.67
МЕТОДЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ РАДИОЛОКАЦИОННЫХ СИСТЕМ
ТЕРАГЕРЦОВОГО ДИаПАЗОНА РАДИОВОЛН
Р. П. Быстров 1, В. Н. Корниенко1 , В. Е. Кузьмичев 2, В. Н. Пожидаев1, С. А. Соколов 1, В. А. Черепенин1
1 Институт радиотехники и электроники им. В.А. Котельникова РАН
2 3 Центральный научно исследовательский институт МО РФ
Статья получена 13 июля 2015 г.
Аннотация. Анализируются возможности имитационного моделирования работы радиолокационной системы терагерцового (ТГц) диапазона радиоволн с разработкой численных моделей и программно-алгоритмического обеспечения исследований распространения электромагнитного импульса в волноводных трактах с конечной проводимостью стенок и процесса дифракции электромагнитного импульса на объектах с дисперсией диэлектрической проницаемости. Рассматривается математическая модель вариантов построения устройств первичной обработки в РЛС ТГц диапазона радиоволн, подтверждающих обоснованность схемотехнических решений и достижения ими заданных характеристик. Предложены алгоритмы оптимальной обработки сигналов РЛС ТГц диапазона для решения задач обнаружения и распознавания физических объектов.
Ключевые слова: диапазон радиоволн, радиолокационная система, электромагнитный импульс, обнаружение (распознавание) объекта, обработка радиолокационного сигнала, численная модель, программное обеспечение, алгоритмы.
Abstract. The possibilities of a computer simulation of radar systems in terahertz (THz) range as the development of numerical models, software and algorithmic support, are investigated. The propagation of electromagnetic pulses in waveguides with finite wall conductivity and the diffraction of electromagnetic pulses on objects with the dispersion of dielectric permittivity are also analyzed. The mathematical model of the devices design for primary processing in modern THz radars, confirming chosen circuit solutions and achieving their desired characteristics, is considered. The complex algorithms are proposed for optimal processing of radar THz range signals to solve problems of detection and recognition of physical objects.
Keywords: frequency band, radar system, electromagnetic pulse, detection (recognition) of an object radar signal processing, numerical model, software, algorithms.
В последние годы повысился интерес к исследованиям особенностей распространения миллиметровых и субмиллиметровых радиоволн в атмосфере, что связано с рядом новых применений их при изучении космического пространства, природных ресурсов Земли, в локации и связи. При создании, например перспективных радиотехнических систем это, прежде всего, связано с совершенствованием радиолокационной техники с высоким разрешением и систем радиосвязи. Применительно к военной технике это вызвано, прежде всего, с тем, что современные боевые действия, чаще стали проводятся в ночных условиях, при задымлениях и в пыли от движущейся техники и разрывов снарядов, что в значительной степени снижается, а иногда и совсем исключается обнаружение и распознавание наземных объектов с помощью оптико-электронных устройств.
Находящиеся в эксплуатации РЛС обнаружения наземных объектов и наведения управляемого оружия, работающие в сантиметровом (СМ) и длинноволновой части миллиметрового (ММ) диапазонах волн, не всегда являются эффективными в распознавании малоразмерных наземных объектов (НО), особенно малоподвижных. Поэтому в подтверждение к выше сказанному требуется создание радиолокационных систем со сверхвысоким разрешением, которые способны на относительно небольших дальностях ~ 1000 - 4500 м, эффективно распознавать медленно движущиеся и неподвижные НО в условиях плохой оптической видимости. Такие радиолокационные системы могут быть базовыми также для систем наведения высокоточного оружия (ВТО) на небольших дальностях или на конечном участке траектории полета боевого баллистического объекта.
Такими более информационными участками СВЧ диапазона радиоволн, располагающиеся в интервалах: в короткой части миллиметрового (ММ) диапазона (длины волн – короче 3 мм: в «окнах прозрачности»: 2.15мм и 1, 3 мм) и в длинноволновой части субмиллиметрового (СБММ) диапазона (длины волн: «в окнах прозрачности»: 0,96 мм; от 0,88мм, 0,34 мм). Данный диапазон волн в указанных “окнах прозрачности” в современной научно-технической литературе стали называть часто терагерцовым (ТГц) диапазоном радиоволн [1-3]. Поэтому и по тексту в данной статье в качестве интересующего нас диапазона волн будем обращаться к ТГц диапазону радиоволн (интервал частот ~ 0,1 – 1 ТГц). Может быть правильнее в дальнейшем такой участок радиоволн и называть, как гигагерцовый (ГГц) диапазон.
Для систем (датчиков ближнего действия) обнаружения (распознавания) объектов и наведения на дальностях не более сотни метров не исключается также возможность исследований с целью освоения и “окон прозрачности” в СБММ диапазоне с длиной волны в районе 0,34 мм. Но это последующая задача.
Данная статья посвящается одному из современных проблемных вопросов в освоении ТГц высокоточных радиолокационных систем, относящихся к разработке методы математического моделирования радиолокационных систем ТГц радиоволн.
Известно, что математическое моделирование, при ответственном его применении, может быть достаточно эффективным инструментом при исследовании вновь создаваемых высокоточных радиолокационной системы. Такое моделирование может позволить не только оценить основные показатели качества работы РЛС еще до создания его экспериментального образца, но и сделать более обоснованным выбор функциональной схемы проектируемого устройства, а также алгоритмов принимаемых им решений.
Однако создание программы моделирования работы РЛС – достаточно сложная и трудоемкая задача. Она сводится к разработке математических моделей тех основных преобразований, которым подвергается р/л сигнал в ходе его обработки различными устройствами РЛС с целью оценки (измерения) тех его параметров, которые несут полезную информацию о цели. Так как любые радиотехнические измерения всегда проводятся на фоне шумов той или иной природы (например, собственного шума приемника), то задачи радиолокационного обнаружения цели и/или измерения ее координат и параметров движения необходимо рассматривать с привлечением статистических методов. Это означает, что математическое моделирование работы РЛС носит характер статистического моделирования.
В данной статье авторами предлагаются для рассмотрения и при необходимости будущей критики ряд научных вопросов, которые, по мнению авторов, являются на данном этапе освоения ТГц диапазона волн, а именно:
- имитационное моделирование работы радиолокатора:
- математические модели вариантов построения устройств первичной обработки в РЛС ТГц диапазона, подтверждающих обоснованность схемотехнических решений и достижения ими заданных характеристик;
- алгоритмы оптимальной обработки сигналов РЛС ТГц диапазона для решения задач обнаружения и распознавания (селекции) объектов техники.
1. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ РАБОТЫ РАДИОЛОКАТОРА
Для разработки программы математического моделирования работы РЛС должны быть известны (заданы):
- зондирующий сигнал, который предполагается использовать в системе, т.е. должны быть заданы законы его амплитудной и, возможно, фазовой (частотой) модуляции;
- характеристики рассеивающих (отражающих) свойств возможных целей (например, ЭПР целей);
- те или иные характеристики среды распространения зондирующего и отраженного от цели сигналов;
- те или иные вероятностные характеристики тех помех, которые сопровождают прием полезного сигнала, отраженного от цели;
- структурная схема РЛС, т.е. последовательность тех математических преобразований (линейных и нелинейных), которым подвергается, при обработке, отраженный от цели сигнал, а также сопровождающая его помеха. Конечным результатом таких преобразований должно быть: либо решение о наличии (или отсутствии) отраженного от цели сигнала (в случае задачи обнаружения), либо измеренные значения тех параметров сигнала, которые несут информацию о положении цели в пространстве и/или о ее состоянии (при решении задачи измерения, например, дальности и скорости цели).
В ходе статистического моделирования работы РЛС могут быть получены оценки следующих основных характеристик качества работы РЛС:
- в случае обнаружения цели: вероятности правильного обнаружения и ложной тревоги, которые обеспечиваются данной системой;
- в случае измерения: среднеквадратические отклонения измеренных значений полезных параметров сигнала от их истинных значений, что однозначно характеризует точность измерения положения и скорости цели.
Компьютерное моделирование может быть проведено на основе комплексной модели, которая должна включать в себя отдельные (вообще говоря, автономные) блоки, описывающие следующие физические процессы:
- формирование и излучение электромагнитного сигнала;
- распространение прямого сигнала до цели;
- рассеяние сигнала на цели и окружающих ее объектах
- распространение рассеянного сигнала в направлении приемной антенны;
- особенности поведения сигнала в приемных трактах устройства.
Кроме того, на основе полученных данных о характеристиках принятого сигнала модель должна обеспечивать проведения обработки данных, позволять осуществлять оптимизацию этой обработки и, при необходимости, вырабатывать управляющие сигналы, направленные как на оптимизацию формы излучаемого сигнала для конкретной радиолокационной обстановки, так и на улучшение работы автоматизированной системы принятия решения.
В связи с этим предлагается следующий состав численной модели:
- блок моделирования прохождения широкополосного электромагнитного сигнала по антенно-фидерным устройствам приемного и передающего трактов;
- блок моделирования распространения сигнала в атмосфере, содержащей гидрометеоры и пр.;
- блок вычисления характеристик рассеивателей различной природы.
В данном разделе дано описание численных алгоритмов, которые могут быть использованы при реализации перечисленных выше блоков.
1.1. Численный алгоритм моделирования распространения электромагнитного импульса в волноводных трактах с конечной проводимостью стенок
Рассмотрим задачу определения пространственно-временных распределений электромагнитного поля в вакуумном объеме V, ограниченном проводящими поверхностями сложной формы. Поле в рассматриваемой системе возбуждается заданным набором источников с известными характеристиками.
Предположим, что диэлектрическая и магнитная проницаемости среды равны единице.
Для решения задачи временной динамики электромагнитного поля можно использовать дифференциальные уравнения Максвелла в пространственно-временном представлении, которые в Гауссовой системе единиц имеют вид:
 ,
,  ,
, 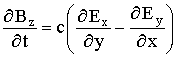 ,
,
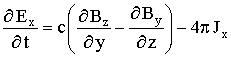 ,
, 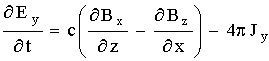 ,
, 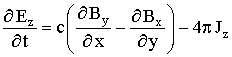 .
.
Рассмотрим три вида граничных условий:
- часть объема V ограничена идеально проводящими поверхностями. При этом тангенциальные составляющие электрического поля на границе области обращаются в ноль. Данное условие может быть использовано в случае, если проводимость ограничивающих объем поверхностей достаточно велика;
- на некоторых границах V выполнено условие излучения плоских волн, т.е. считается справедливым предположение, что структура электромагнитного поля вблизи границы области соответствует структуре плоской волны, волновой вектор которой параллелен нормали к поверхности. Такой вид граничных условий используется при описании открытых концов волноведущих трактов;
- объем содержит тела с конечной проводимостью. В этом случае на границе тел следует учитывать возбуждаемые поверхностные токи, величина которых, согласно закону Ома, пропорциональна действующему значению напряженности электрического поля.
Составим конечно-разностную аппроксимацию системы
уравнений. Для каждой из компонент введем в объеме V
пространственную сетку ![]() , узлы которой удовлетворяют
следующим рекурентным соотношениям:
, узлы которой удовлетворяют
следующим рекурентным соотношениям:
для Bx компоненты
![]()
![]()
![]()
для By компоненты
![]()
![]()
![]()
для Bz компоненты
![]()
![]()
![]()
для Ex компоненты
![]()
![]()
![]()
для Ey компоненты
![]()
![]()
![]()
для Ez компоненты
![]()
![]()
![]()
где ![]() - шаг пространственной сетки,
- шаг пространственной сетки, ![]() ,
,![]() ,
,![]() - количество узлов сетки по координатам x, y, и z
соответственно.
- количество узлов сетки по координатам x, y, и z
соответственно.
Такое расположение сеток дает возможность использовать центрированную схему аппроксимации пространственных производных. Взаимное расположение пространственных сеток представлено на рис. 1.
Узлы пространственных сеток компонент плотности тока совпадают с узлами соответствующих компонент электрического поля.
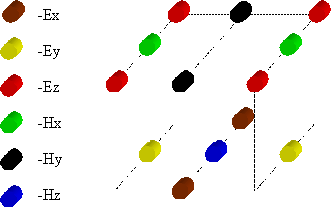
Рис.1. Пространственное расположение узлов сеток компонент электромагнитного поля.
Введем шаг
по времени ![]() ,
величина которого удовлетворяет условию Куранта:
,
величина которого удовлетворяет условию Куранта:
![]()
где ![]() - безразмерный коэффициент, величина которого зависит
от конкретной конфигурации проводников и характерных частот рассматриваемых
процессов. Значения сеточных функций компонент магнитного поля вычисляются в
моменты времени
- безразмерный коэффициент, величина которого зависит
от конкретной конфигурации проводников и характерных частот рассматриваемых
процессов. Значения сеточных функций компонент магнитного поля вычисляются в
моменты времени ![]() , такие, что:
, такие, что:
![]()
Электрическое поле определяется в моменты времени
![]()
Используя описанный сдвиг временных сеток, можно получить следующие конечно-разностные соотношения:



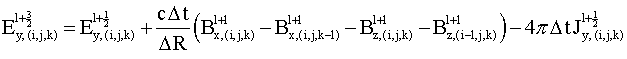
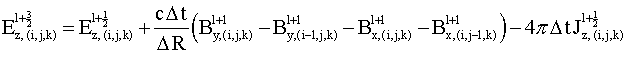
Здесь верхний индекс обозначает момент времени, нижний индекс до открывающейся круглой скобки - компоненту поля, нижние индексы в круглых скобках обозначают номер узла пространственной сетки.
Для решения задачи формирования электромагнитного поля в большинстве случаев используются нулевые начальные условия: значения компонент электромагнитного поля во всех точках рассматриваемого объема равны нулю, и сторонние токи в системе отсутствуют.
1.2. Численная модель процесса дифракции электромагнитного импульса на объектах с дисперсией диэлектрической проницаемости
Рассмотрим прямоугольную область свободного пространства, содержащую набор диэлектрических тел со сложной границей (рис.2).
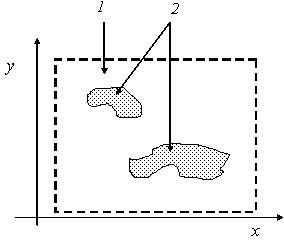
Рис. 2. Общий вид рассматриваемой системы:
1 - область построения решения, 2 - диэлектрические тела.
Пусть в направлении положительных значений координат оси х распространяется импульс микроволнового излучения с известной частотой заполнения и заданной формой огибающей. Зависимость действительной и мнимой частей диэлектрической проницаемости тел от частоты считается известной. Характерные линейные размеры тел лежат в диапазоне от нескольких десятых долей длины волны до десятков длин волн падающего излучения.
Расстояния же между рассеивателями произвольны. В этих условиях необходимо определить динамику полного (т.е. падающего и рассеянного) электромагнитного поля.
Для описания нестационарной динамики электромагнитного поля воспользуемся системой уравнений Максвелла в пространственно-временном представлении:
где ![]() ,
, ![]() -
напряженность электрического и магнитного поля соответственно,
-
напряженность электрического и магнитного поля соответственно, ![]() - индукция магнитного поля. Для рассматриваемого
класса диэлектриков магнитная проницаемость с хорошей точностью равна единице,
поэтому
- индукция магнитного поля. Для рассматриваемого
класса диэлектриков магнитная проницаемость с хорошей точностью равна единице,
поэтому ![]() .
.
В (1,2)
учтена связь между векторами электрической индукции ![]() ,
напряженности электрического поля и поляризацией среды (дипольным моментом
единицы объема)
,
напряженности электрического поля и поляризацией среды (дипольным моментом
единицы объема) ![]() :
:
|
|
(3) |
Для вычисления дипольного момента единицы объема будем использовать осцилляторную микроскопическую модель среды [4], т.е. дипольный момент будет определяться отклонениями зарядов-осцилляторов от положения равновесия под действием внешней силы, а именно:
|
|
(4) |
где ![]() - количество электронов в единице объема вещества.
- количество электронов в единице объема вещества.
Уравнение движения одного осциллятора с учетом потерь имеет вид
где k -
эффективная жесткость; ![]() -
коэффициент затухания; m, e - масса и заряд электрона.
-
коэффициент затухания; m, e - масса и заряд электрона.
Совместное решение (1, 2, 4, 5) дает возможность определить динамику поля с учетом дисперсии комплексной диэлектрической проницаемости объектов, входящих в рассматриваемую систему.
Решение полученной системы уравнений будем проводить численно. Частные производные в уравнениях электромагнитного поля аппроксимируем конечными разностями. Для удобства моделирования открытых (с точки зрения излучения) границ области удобно дополнить (2) членом, содержащим ток проводимости. Тогда на границах области построения решения можно будет ввести неоднородный поглощающий слой, характеристики которого обеспечат практически полное отсутствие отражений электромагнитных волн от границ.
В
прямоугольной области для каждой из компонент электромагнитного поля введем
пространственную сетку ![]() , координаты узлов которой
удовлетворяют следующим рекуррентным соотношениям:
, координаты узлов которой
удовлетворяют следующим рекуррентным соотношениям:
для Bz компоненты
![]() .
.
![]() ,
,
для Ex компоненты
![]() ,
,
![]() ,
,
для Ey компоненты
![]() ,
,
![]() ,
,
где ![]() - шаг пространственной сетки,
- шаг пространственной сетки, ![]() ,
,![]() - количество узлов сетки по координатам
x, y соответственно. Такое взаимное
расположение сеток дает возможность использовать центрированную схему
конечно-разностной аппроксимации пространственных производных и обеспечивает
устойчивость разностной схемы.
- количество узлов сетки по координатам
x, y соответственно. Такое взаимное
расположение сеток дает возможность использовать центрированную схему
конечно-разностной аппроксимации пространственных производных и обеспечивает
устойчивость разностной схемы.
Введем
шаг по времени ![]() , величина которого
удовлетворяет условию Куранта:
, величина которого
удовлетворяет условию Куранта:
|
|
где
![]() - безразмерный
коэффициент, величина которого зависит от конкретной конфигурации проводников и
характерных частот рассматриваемых процессов.
- безразмерный
коэффициент, величина которого зависит от конкретной конфигурации проводников и
характерных частот рассматриваемых процессов.
Значения
сеточных функций компонент магнитного поля вычисляются в моменты времени ![]() ,
такие, что:
,
такие, что:
|
|
Электрическое поле определяется в моменты времени
|
|
При таком сдвиге по времени между вычислениями магнитных и электрических составляющих поля, конечно-разностная аппроксимация уравнений Максвелла имеет вид:
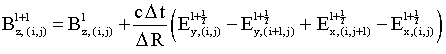 ,
,
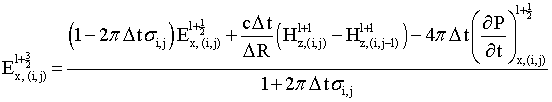 ,
,
 .
.
Здесь верхний индекс обозначает момент времени, нижний индекс до открывающейся круглой скобки - компоненту поля, нижние индексы в круглых скобках обозначают номер узла пространственной сетки.
Величина
![]() определяется скоростью осцилляторов в
текущий момент времени
определяется скоростью осцилляторов в
текущий момент времени
|
|
Для численного интегрирования уравнения (5) удобно использовать схему "с перешагиванием".
|
|
|
|
1.3. Программа расчета импульсной переходной характеристики
Алгоритм расчета импульсной характеристики уединенного рассеивателя основан на использовании численной схемы, описанной в п.2. и состоит из следующих шагов.
1. Задание геометрической формы рассеивающего тела. Форма задается с точностью до долей длины волны падающего на тело электромагнитного поля.
2. Задание электромагнитных свойств материала тела. На данном шаге по известным экспериментальным данным о дисперсионных свойствах диэлектрической проницаемости рассматриваемого объекта выбираются параметры осцилляторов, описывающих реакцию среды на внешний электромагнитный импульс.
3. Задание характеристик зондирующего импульса микроволнового излучения, которые выбираются исходя из значений излучаемой длины волны и поляризации падающего поля. А именно, зондирующий импульс должен содержать в себе один период колебаний электромагнитного поля, его длительность должна быть короче на порядок по сравнению с периодом реально излучаемого поля. В этом случае с хорошей степенью точности можно утверждать, что воздействие на рассеиватель выбранного импульса близко к воздействию дельта-образного возмущения. Т.е. полученное в результате рассеянное поле будет близко к искомой импульсной характеристике.
4. Проведение моделирования динамики полного поля с использованием описанной в п.2. модели.
5. Выделение из общего поля рассеянного.
Шаги 4-5 повторяются для различных значений углов падения зондирующего импульса на исследуемый объект.
На рис.3 приведена блок-схема программы, реализующей предложенный выше алгоритм.
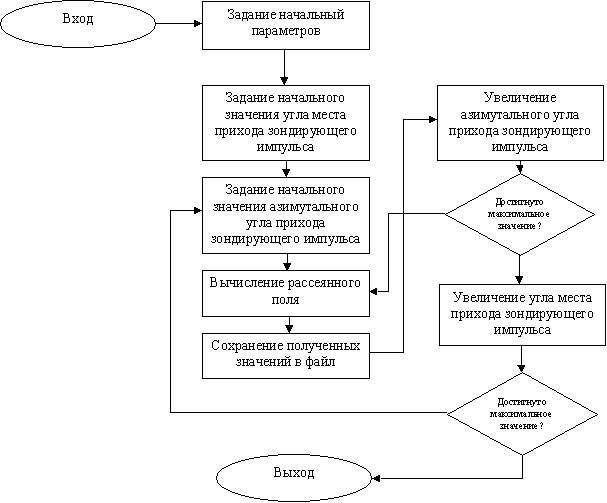
Рис.3. Блок-схема программы.
Для определения рассеянного поля используется набор точек наблюдения, которые располагаются на поверхности воображаемой сферы, центр которой совпадает с геометрическим центром рассеивающего тела. Радиус сферы должен быть много больше характерных линейных размеров рассеивателя и может составлять много длин волн.
В выбранных точках фиксируются значения компонент электромагнитного поля в каждый момент времени. По полученным временным реализациям строится импульсная характеристика, которая является функцией четырех угловых координат (центр системы координат располагается в геометрическом центре рассеивающего тела): азимутального угла и угла места прихода зондирующего импульса, азимутального угла и угла мета направления, в котором распространяется рассеянное волновое поле.
Программа имитационного моделирования рассеивания короткого электромагнитного импульса. Рассмотрим процесс формирования электромагнитного поля, возникающего в результате отражения заданного зондирующего импульса микроволнового излучения на наборе тел произвольной формы. Предположим, что импульсные характеристики рассеяния для каждого тела, включенного в набор, уже известны (например, в результате работы программы, описанной выше).
Если тела, входящие в набор, достаточно удалены друг от друга, то допустимо предположение о слабом влиянии переотражений рассеянного поля на каждом из тел рассматриваемого набора.
В этом случае суммарное волновое поле, образованное за счет однократного рассеяния зондирующего импульса на каждом из тел, и распространяющееся в заданном направлении (например, в направлении приемной антенны), вычисляется при помощи следующего алгоритма.
1. В точке расположения каждого из тел набора определяется значение падающего поля (временные зависимости компонент электромагнитного поля).
2. При помощи алгоритма быстрого преобразования Фурье вычисляется комплексный спектр падающего излучения.
3. Полученный спектр умножается на спектр импульсной характеристики для заданного направления распространения как зондирующего импульса, так и рассеянного волнового поля.
4. Используя обратное преобразование Фурье, получаем временную реализацию рассеянного поля, созданного одним объектом.
Выполнив шаги алгоритма 1-4 для каждого из тел набора, с учетом фазовых сдвигов, определяемых взаимным расположением тел, проводится суммирование временных реализаций рассеянного поля.
Если пренебречь многократными отражениями невозможно, программа имитационного моделирования использует итерационный алгоритм, основанный на процедуре, описанной ранее, а именно, в качестве первого приближения вычисляется поле однократного рассеяния. Далее проводится суммирование рассеянного поля и поля зондирующего импульса в каждой точке, соответствующей положению тел набора. Полученное в результате суммарное волновое поле выступает в качестве поля зондирующего импульса процедуры, описанной ранее. Выход из итерационной процедуры осуществляется при достижении заранее заданной точности вычисления рассеянного поля.
Таким образом, предложенный набор алгоритмов позволяет проводить предварительный анализ волновых полей широкого диапазона частот, образованных в результате рассеяния зондирующего импульса произвольной формы на наборе тел различной природы.
Примерная структура программы для имитационного моделирования на ПК. Необходимо создать программу для расчета на персональном компьютере имитации работы радара для различных погодных условий, параметров цели и моментов времени. Программа на первом этапе моделирует временной ход сигнала, регистрируемого приемником радара. На втором этапе этот сигнал анализируется и по нему делаются выводы о наличии цели и ее характеристиках. По структуре программа разделяется на пять блоков.
Блок ввода входных параметров для расчета, который сам разделяется на три части:
параметры радара: (длина волны l[мкм], длительность импульса t[нс], время между импульсами T[c], расходимость радиолуча j[мрад] или диаграмма направленности антенны G, эффективная площадь приемной антенны SA, мощность в импульсе РТ [Вт], минимальная принимаемая приемником мощность [Вт];
параметры объекта: индекс цели (1-танк, 2-орудие и т.д.), индекс фона (1-лес, 2-поле и т.д.), дальность до цели L[км], вектор скорости цели V0[м/c] и азимут f[град];
параметры атмосферы: давление Р, температура q, влажность воздуха W, модель атмосферы (М=0 – чистая, М=1 – туман, М=3 – дождь, М=4 – снегопад, М=5 – пыль, М=6 – дым), интенсивность метеоявления (в зависимости от величины М вводим: водность тумана qT [г/м3], интенсивность дождя R[мм/час], интенсивность снегопада I[мм/час], запыленность воздуха qП [г/м3], задымленность воздуха qД [г/м3].
Блок промежуточных расчетов, где рассчитываются: ЭПР цели, ЭПР фона, удельная ЭПР метеоявления (при его наличии), коэффициент ослабления радиоволн в чистой атмосфере, коэффициент ослабления радиоволн в замутненной атмосфере.
Здесь используются соответствующие банки данных и инженерные алгоритмы расчетов требуемых величин.
Блок основного расчета, где в цикле по времени находится принимаемая радаром мощность при реализации всех входных параметров, а также рассчитывается отношение сигнал/шум (о.с.ш.). При желании на экран монитора выводится, например, график, показывающий величину (о.с.ш.) в зависимости от времени, прошедшего с момента излучения импульса. Параметры шумового сигнала можно варьировать.
Блок анализа, где делается обработка результатов основного расчета с целью нахождения параметров цели и ее распознавания. Определяется (о.с.ш.), обеспечивающее обнаружение с заданной вероятностью при заданном уровне ложных тревог. Оцениваются вероятностные критерии полученной информации.
Блок вывода результатов расчета.
По окончании расчета выдается запрос на повтор вычислений с изменением входных параметров.
2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВАРИАНТОВ ПОСТРОЕНИЯ УСТРОЙСТВ ПЕРВИЧНОЙ ОБРАБОТКИ В РЛС ТЕРАГЕРЦОВОГО ДИАПАЗОНА
Компьютерная модель позволяет рассчитывать величину отношения принимаемой мощности к мощности импульсного передатчика на выбранных длинах волн в исследуемом диапазоне в зависимости от дальности до цели и различных метеорологических условиях, а также путем корреляционного анализа принимаемого и излученного импульсов находить дальность до цели. В первоначальном проекте предполагалось задавать различный вид излучаемого импульса и различные методы первичной обработки информации, а также движение цели. Но из-за приостановки финансирования эти варианты в программе реализованы не были, хотя при задании входных параметров эти возможности упоминаются.
В данной реализации программы математического моделирования расчет проводится по стандартной формуле радиолокации. Параметры атмосферы задаются следующим образом. Пользователь может выбрать один из сезонов года (определяя тем самым поглощение радиоволн в газах атмосферы) с добавлением (при желании) различных осадков или аэрозолей с разной интенсивностью. Данные о молекулярном поглощении приняты для г. Дубна Московской области. Наличие на трассе РЛС, например, дождя создает распределенную ложную цель, параметры которой также рассчитываются. Делается описание самой программы и инструкций для пользователя.
Программа имитационного моделирования (ПИМ) предназначена для проведения расчетов интенсивности (мощности) принятого радиолокационным комплексом сигнала при заданных характеристиках: излучаемого импульса; передающего тракта; излучающей антенны; трассы распространения сигнала, включая метеоявления и сезонность; импульса, отраженного от цели, включая подстилающую поверхность; приемной антенны; приемного тракта; приемника [1]. Также ПИМ выполняет корреляционный анализ огибающей принятого сигнала.
2.1. Общая структура программы
ПИМ состоит из трех основных блоков (рис.4): блок задания параметров; вычислительный блок; интерфейс пользователя.
Первый блок предназначен для формирования полного списка параметров, необходимых для проведения имитационного моделирования. Эти параметры описывают характеристики генератора, передающего тракта, излучающей антенны, открытой трассы, цели, приемной антенны, приемного тракта, собственно приемника.
Вычислительный блок обеспечивает расчет интенсивности электромагнитного поля, формируемого излучающей антенной с учетом ее диаграммы направленности, в окружающем пространстве. Здесь же проводится вычисление поля, отраженного от цели, от осадков и от подстилающей поверхности. Временная зависимость интенсивности принятого сигнала используется для проведения корреляционной обработки.
Третий блок обеспечивает взаимодействие пользователя с ПИМ, обрабатывает задаваемые им команды и пр.
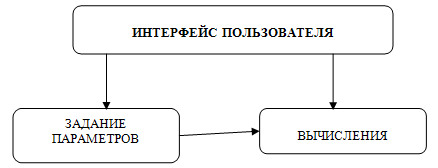
Рис.4. Основные блоки
программы и их взаимодействие
2.2. Программная реализация
При разработке ПИМ был использован объектно-ориентированный подход с учетом требований возможной межплатформенной переносимости исполняемого кода. В связи с этим было принято решение об использовании технологии «.NET».
Приложение написано на языке программирования C# и содержит набор модулей, список и функциональное назначение которых приведены в табл. 1.
Таблица 1. Список основных модулей ПИМ
|
№№ п/п |
Название |
Размер (кБайт) |
Назначение |
|
1 |
Program.cs |
21 |
Содержит основной цикл приложения, класс описания глобальных переменных, общие процедуры обработки параметров и данных |
|
2 |
main_frame.cs |
22 |
Основное окно интерфейса пользователя. Содержит панель задания параметров и панель вычислений |
|
3 |
main_frame.Designer.cs |
63 |
Содержит описание примитивов, использованных в main_frame.cs |
|
4 |
param_emm_form.cs |
7 |
Диалоговое окно задания параметров передатчика |
|
5 |
param_emm_form.Designer.cs |
13 |
Содержит описание примитивов, использованных в param_emm_form.cs |
|
6 |
param_emm_trakt_form.cs |
6 |
Диалоговое окно задания параметров передающего тракта |
|
7 |
param_emm_trakt_form.Designer.cs |
10 |
Содержит описание примитивов, использованных в param_emm_trakt_form.cs |
|
8 |
param_emm_ant_form.cs |
7 |
Диалоговое окно задания параметров передающей антенны |
|
9 |
param_emm_ant_form.Designer.cs |
15 |
Содержит описание примитивов, использованных в param_emm_ant_form.cs |
|
10 |
param_recv_form.cs |
6 |
Диалоговое окно задания параметров приемника |
|
11 |
param_recv_form.Designer.cs |
11 |
Содержит описание примитивов, использованных в param_recv_form.cs |
|
12 |
param_recv_trakt_form.cs |
6 |
Диалоговое окно задания параметров приемного тракта |
|
13 |
param_recv_trakt_form.Designer.cs |
10 |
Содержит описание примитивов, использованных в param_recv_trakt_form.cs |
|
14 |
param_recv_ant_form.cs |
7 |
Диалоговое окно задания параметров приемной антенны |
|
15 |
param_recv_ant_form.Designer.cs |
15 |
Содержит описание примитивов, использованных в param_recv_ant_form.cs |
|
16 |
param_trassa_form.cs |
6 |
Диалоговое окно задания параметров трассы распространения сигнала |
|
17 |
param_trassa_form.Designer.cs |
21 |
Содержит описание примитивов, использованных в param_trassa_form.cs |
|
18 |
param_target_form.cs |
6 |
Диалоговое окно задания параметров цели |
|
19 |
param_target_form.Designer.cs |
18 |
Содержит описание примитивов, использованных в param_target_form.cs |
|
20 |
calc.cs |
9 |
Содержит функции обработки принятого сигнала |
|
21 |
param_procs_form.cs |
2 |
Диалоговое окно задания параметров обработки принятого сигнала |
|
22 |
param_procs_form.Designer.cs |
6 |
Содержит описание примитивов, использованных в param_procs_form.cs |
Описание интерфейса пользователя приведено в [1]. Там же приводится и примерный порядок работы пользователя.
3. АЛГОРИТМЫ ОПТИМАЛЬНОЙ ОБРАБОТКИ СИГНАЛОВ РЛС ТЕРАГЕРЦОВОГО ДИАПАЗОНА ДЛЯ РЕШЕНИЯ ЗАДАЧ ОБНАРУЖЕНИЯ И РАСПОЗНАВАНИЯ (СЕЛЕКЦИИ) ОБЪЕКТОВ ТЕХНИКИ
Так как предполагается, что благодаря особенностям ТГц диапазона радиочастот радиолокационной (РЛ) системы она способна строить радиоизображения объектов, находящихся в заданной области пространства, то технически наиболее целесообразно получать их путем сканирования этой области с помощью узкой диаграммы направленности. В результате сканирования вся исследуемая область разбивается на отдельные угловые элементы разрешения. Анализируя колебание, приходящее от каждого такого элемента, приемник РЛ системы должен принять решение о том есть ли в нем сигнал, отраженный от цели, или его нет. В случае обнаружения цели ей приписываются угловые координаты, соответствующие положению того элемента разрешения, для которого было принято это решение, а также измеряются ее дальность и, возможно, скорость. При этом если угловые размеры цели меньше соответствующих размеров элемента разрешения, то цель считается сосредоточенной. Если же обнаруживаемый объект занимает несколько угловых элементов разрешения, то можно говорить о протяженной цели. В последнем случае появляется возможность определения ее формы и размеров. Таким образом, одним из центральных моментов при разработке РЛ системы является нахождение алгоритмов обработки РЛ сигналов, позволяющих обнаруживать и измерять координаты и параметры движения цели.
Так как только небольшая часть энергии зондирующего сигнала, отразившегося от цели, достигает приемного устройства РЛС, то процесс РЛ наблюдения должен рассматриваться с учетом шумов, которые всегда сопровождают сигнал и которые представляют собой реализации тех или иных случайных процессов. Отсюда следует, что теория синтеза систем РЛ наблюдения должна, по необходимости, опираться на известные положения математической статистики, то есть являться статистической теорией. В настоящее время существует достаточно развитая статистическая теория синтеза систем РЛ наблюдений, позволяющая находить алгоритмы обработки радиолокационных сигналов оптимальные с точки зрения выбранных критериев качества их работы [5-12].
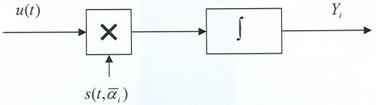
Для решения задачи синтеза оптимальных систем обнаружения и измерения должны быть заданы: 1) вид зондирующего сигнала и соответствующее выражение для сигнала, отраженного от цели; 2) вероятностные характеристики помех (шумов), сопровождающих прием полезного сигнала; 3) критерии качества работы РЛ системы в режимах обнаружения и измерения. Кратко рассмотрим каждый из этих пунктов.
Зондирующий сигнал ![]() представляет собой узкополосный сигнал,
модулированный, в общем случае, как по амплитуде, так и по фазе (частоте),
который может быть записан в следующем виде:
представляет собой узкополосный сигнал,
модулированный, в общем случае, как по амплитуде, так и по фазе (частоте),
который может быть записан в следующем виде:
|
(6) |
|
(7) |
|
(8) |
3.1. Оптимальная обработка радиолокационных сигналов, отраженных от медленно флуктуирующих точечных объектов
|
(9) |
|
(10) |
|
(11) |
|
(12) |
|
|
(13) |
|
|
(14) |
|
|
(15) |
|
|
|
|
(16) |
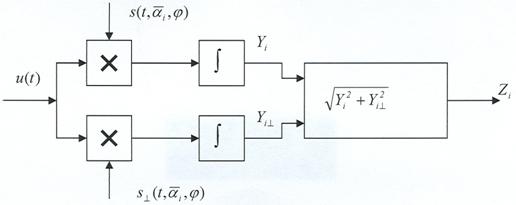
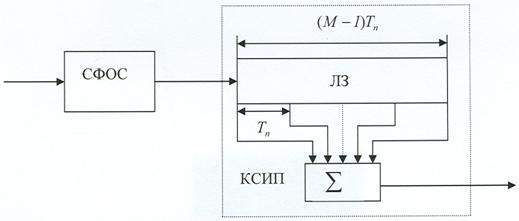
Рис. 5. Многоканальная схема оптимальной обработки.
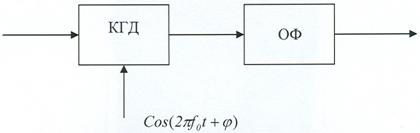
Рис.6. Схема корреляционного канала обработки.
|
(17) |
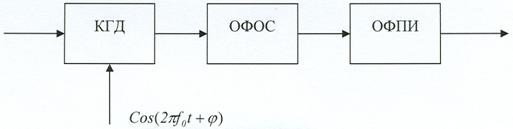
Рис. 7. Схема формирования корреляционного интеграла методом оптимальной фильтрации.
|
|
|
|
|
(18) |
|
|
(19) |
|
(20) |
Рис. 8. Схема оптимального корреляционного канала обработки сигналов со случайной начальной фазой
Рис. 9. Схема обработки сигналов со случайной начальной фазой методом оптимальной фильтрации.
|
(21) |
|
(22) |
|
(23) |
|
(24) |
|
|
|
|
|
|
|
(25) |
|
(26) |
|
(27) |
|
(28) |
|
|
|
|
(29) |
|
(30) |
|
|
|
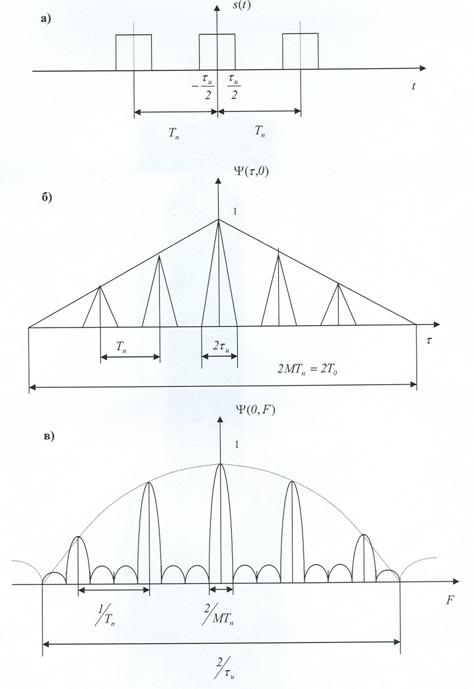
Рис. 10. Сечения функции
неопределенности ![]() прямоугольной
прямоугольной
когерентной пачки прямоугольных радиоимпульсов.
|
(31) |
|
(32) |
|
(33) |

a)
b)
a)
b)

a)
3.2. Оптимальная обработка радиолокационных сигналов, отраженных от точечных целей с доплеровским рассеянием
|
(34) |
|
|
|
|
(35) |
|
|
(36) |
|
|
|
|
|
|
|
(37) |
|
(38) |
|
|
|
|
(39) |
3.3. Оптимальная обработка радиолокационных сигналов, отраженных от протяженных медленно флуктуирующих целей
|
(40) |
|
|
(41) |
|
|
(42) |
|
|
(43) |
|
(44) |
|
(45) |
|
|
(46) |
|
|
(47) |
|
(48а) |
|
|
(48б) |
|
|
(49) |
|
|
(50) |
|
|
3.3.4. Оптимальная обработка радиолокационных сигналов, отраженных от целей с рассеянием по двум параметрам
|
(52) |
|
|
(53) |
|
(54) |
|
|
(55) |
|
|
(56) |
|
|
(57) |
|
|
(58) |
|
|
(59) |
|
|
(60) |
|
|
|
|
|
(61) |
|
|
|
|
|
(62) |
|
|
3.5. Автоматическая классификация (распознавание объектов)
Распознавание цели – это определение типа цели путем анализа данных о ее параметрах движения и поведения, характере ее излучений и других данных, поступающих с РЛС. Задача распознавания типа цели в радиолокации является одной из наиболее сложных, причем основная сложность заключается в определении набора признаков отраженного сигнала, по которым и проводится распознавание. В качестве признаков могут использоваться амплитудные и фазовые спектры отраженных сигналов, поляризационные характеристики (элементы поляризационной матрицы рассеяния), статистические характеристики элементов радиолокационного портрета цели (при сверхразрешении по дальности), баллистические и тактические свойства объекта и многие другие.
Решение задачи классификации цели выполняется классификатором на основании анализа значений признаков, поступающих на его вход с выхода выделителя признаков. Высшим уровнем решения этой задачи является распознавание обнаруженного объекта по его изображению до типа и состояния (например, танк MI в движении), средним уровнем – распознавание до вида (танк), низшим – распознавание объекта по одному или нескольким признакам до класса (объект бронетанковой техники). В роли классификатора может выступать как человек, анализирующий и интерпретирующий входные данные, представленные в этом случае, как правило, в виде изображения, так и автоматическое устройство. Далее будем рассматривать только автоматический режим работы классификатора.
Основу работы автоматических классификаторов составляют алгоритмы, построенные для решения задач распознавания образов. Ниже, очень кратко приведем постановку задачи распознавания образов в ее формальном, математическом плане, а также опишем некоторые из наиболее распространенных методов ее решения, которые могут быть использованы при решении задач распознавания. Обычно области существования признаков различных типов целей перекрываются, поэтому для распознавания применимы методы теории решений. Фактически во многих методах распознавания используются критерии отношения правдоподобия. Применяются и некоторые другие методы: обучающиеся машины, искусственный интеллект и так далее [19].
В формальном математическом плане задача формулируется следующим образом. Допустим у каждого входного образа (сигнала от цели) измеряется N признаков. Каждое множество из N признаков можно рассматривать как вектор X, называемый вектором признаков, или как точку в N-мерном пространстве признаков:

Задача распознавания образов или автоматической
классификации ставится следующим образом. Пусть наблюдается некоторая,
интересующая нас система, которая может находиться в одном из M
различных состояний: ω1, ω2,… ωM. Однако то состояние, в котором система находится
на момент наблюдения, нам не известно. Могут быть известны только вероятности
(априорные) нахождения системы в этих состояниях: Р(ω1), Р(ω2),…
Р(ωМ), причем  . Кроме того, мы можем измерять те или иные параметры системы : Х1,
Х2, …ХN.. Задача распознавания (различения, классификации)
заключается в том, что зная измеренные значения этих параметров, надо принять
решение о том, в каком состоянии находится система. Другими словами, необходимо
найти алгоритм работы автоматического устройства, которое при предъявлении ему
на вход измеренных значений параметров системы Х формировало бы на своем выходе
решение о состоянии, в котором находится система ω.
. Кроме того, мы можем измерять те или иные параметры системы : Х1,
Х2, …ХN.. Задача распознавания (различения, классификации)
заключается в том, что зная измеренные значения этих параметров, надо принять
решение о том, в каком состоянии находится система. Другими словами, необходимо
найти алгоритм работы автоматического устройства, которое при предъявлении ему
на вход измеренных значений параметров системы Х формировало бы на своем выходе
решение о состоянии, в котором находится система ω.
Решение задачи распознавания во многом определяется априорной информацией относительно исследуемой системы и условий ее наблюдения.
Механизм случайности, который формирует вектор наблюдения Х, приводит к тому, что любое решение, которое мы принимаем, может оказаться ошибочным. Поэтому все, что мы можем сделать, это попытаться построить устройство принятия решений минимизирующее, в том или ином смысле, возможность принятия таких неправильных решений.
Существует несколько математических подходов к решению этой задачи. Наиболее последовательным и наиболее общим является байесовский подход. Если он может быть реализован, то он обеспечивает наилучший результат (минимум среднего риска), который может быть получен на основании имеющейся у нас информации. К сожалению условия распознавания чаще всего недостаточны для построения байесовского оптимального алгоритма, поскольку чаще всего неизвестны априорные вероятности Р(ω1), Р(ω2),… Р(ωМ).
Тем не менее, в теории распознавания образов было предложено много подходов к решению задач классификации при том или ином, неполном объеме априорной информации. Если попытаться коротко охарактеризовать все эти подходы и предлагаемые при этом алгоритмы, то все они сводятся к следующему. Пусть нам задана априорная информация об условиях распознавания в том или ином объеме, но в любом случае недостаточном для построения байесовского оптимального алгоритма. Тогда задача заключается в том, чтобы найти такие правила классификации которые, во-первых, опирались бы только на эту априорную информацию и во-вторых, давали бы решение задачи распознавания, по возможности, наилучшее среди всех других правил, опирающихся на тот же самый объем априорных данных [20, 21].
Существует еще одна группа методов распознавания, которая не требует знания плотностей вероятности. Это классификация образов по критерию минимума расстояния. Так в некоторых случаях образы любого из рассматриваемых классов проявляют тенденцию к тесной группировке вокруг некоторого образа, являющегося типичным или репрезентативным для соответствующего класса. При решении задач обнаружения в качестве такого типичного образа могут быть, например, взяты образы танка, орудия, джипа и тому подобных объектов.
Итак, имеем М классов и пусть эти классы допускают представление с помощью эталонных образов: z1, z2, …zM. Евклидово расстояние между произвольным вектором образа Х и i-ым эталоном определяется следующим выражением:
![]() , где Т – символ
транспонирования матрицы.
, где Т – символ
транспонирования матрицы.
Классификатор, построенный по принципу минимума расстояния, вычисляет расстояние, отделяющее неклассифицированный образ Х от эталона каждого класса и зачисляет этот образ в класс, оказавшийся ближайшим к нему. Другими словами, образ Х приписывается к классу zi, если условие Di < Dj выполняется для всех j≠i. Случаи равенства расстояний разрешаются произвольным образом.
Практическим препятствием применения классификации методами минимизации расстояния является то обстоятельство, что для достижения заданных границ качества классификации необходимо сохранять в памяти большое число образов, о которых известна принадлежность их некоторому классу. Кроме того, при осуществлении классификации необходимо вычислять расстояния между каждым классифицируемым образом и всеми образами, хранящимися в памяти системы.
Поэтому, к сожалению, кроме математических трудностей решения задачи распознавания возникают еще и практические, поскольку в этом случае РЛС надо снабдить высокопроизводительным вычислительным устройством – «мозгом» как для обработки поступающей информации, так и для принятия решения, сопоставляя в соответствии со специальными алгоритмами предварительные данные об объектах, заложенные в память (банк данных) и текущую информацию с РЛС. Сложность решения задачи распознавания объектов усугубляется еще и тем, что анализ информации проводится не в статическом, а в напряженном динамическом режиме и при остром дефиците времени. Изображения целей должны обрабатываться системой при непрерывно меняющихся ракурсах и масштабах, на различных подстилающих фонах. Все это может привести к необходимости применения компьютеров с несравненно большим быстродействием, чем у современных устройств.
Таким образом, система распознавания пока не относится к списку первоочередных задач, возникающих при создании РЛС. На более позднем этапе для создания такой системы целесообразно будет привлечь специализированную организацию. Так РУП «КБ Радар» (Белоруссия) [22] производит разработку алгоритмов и систем распознавания классов целей для любых существующих и перспективных радиолокаторов. Разрабатываемые этим КБ системы радиолокационного распознавания предназначены для автоматического распознавания классов обнаруженных или сопровождаемых целей на основании детального анализа отраженных от них радиолокационных сигналов.
Литература
1. Баранов Н.А., Быстров Р.П., Гвоздев А.Е., Корниенко В.Н., Пожидаев В.Н., Немцов А.В. Возможности и особенности применения терагерцового диапазона волн в высокоточных системах наведения. Монография. // Типография ФГКУ 3 ЦНИИ М.О России, 2013. - 357 с.
2. Кинев Николай Вадимович. Генерация и прием ТГц излучения использованием сверхпроводниковых интегральных устройств. Диссертации на соискание ученой степени кандидата физико-математических наук. // ИРЭ им. В.А. Котельникова РАН, Москва 2012.
3. Разработка и применение технологий ТГц- диапазона (Пер. Ломако А.А., ВИНИТИ РАН) MillitaryTechnology. - 2010. – 34. –P.16-19.
4. Ландсберг Г.С. Оптика. - М.:ФИЗМАТЛИТ, 2003. - 848 с.
5. Теоретические основы радиолокации. Под ред. Я.Д. Ширмана. М. Сов. радио, 1970.
19. Дуда Р., Харт П. Распознавание образов и анализ сцен. М. "Мир", 1976.
20. Ту Дж., Гонсалес Р. Принципы распознавания образов. М. "Мир", 1978.
21. Фукунага К. Введение в статистическую теорию распознавания образов. М. "Наука", 1979.
22. КБ Радар. Системы радиолокационного распознавания [электронный ресурс]. URL: http://www.kbradar.by/text/pages-view-15.html.