| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 6 , 2000 |
ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ ЛИНЕЙНОГО ПЕРЕМЕННОГО ТОКА В ПЛОСКОСЛОИСТОЙ СРЕДЕ
В.С. Семенов, В.Г. Дыбовский, А.В. Неведомский
Сибирский физико-технический институт при Томском Государственном университете
Получена 13 июня 2000 г.
Приведено строгое и приближенное решения задачи. Оценена область применимости приближенных формул. Приведены результаты численных расчетов компонент поля.
Вопросам расчета электромагнитного поля линейного переменного тока, расположенного в полупространстве, либо в одном из слоев многослойной проводящей среды, посвящено большое количество теоретических и экспериментальных работ [1-5]. Для некоторых частных случаев получено решение в конечном виде. Численные исследования, как правило, не проводились. Открытым оставался также вопрос о влиянии границ раздела, электрических параллельных слоев и частоты на структуру поля линейного тока, погруженного в слоистую среду.
Исследования, проведенные в данной статье, преследуют две основные цели. Во-первых, оценить влияние среды и применяемой частоты на структуру поля. Во-вторых, оценить область применимости приближенных формул.
Приведем краткое описание строгого и приближенного метода.
1. Решение методом Зоммерфельда.
Строгий аналитический расчет компонент поля линейного переменного тока, расположенного в одном из слоев многослойной проводящей среды с плоско-параллельными поверхностями раздела, может быть выполнены методом Зоммефельда [1]. Суть метода заключается в следующем.
Полагаем,
что линейный ток находится под слоем
конечной проводимости в трехслойной среде рис.1.
Считаем, что существует лишь составляющая
вектор-потенциала параллельная току, то
есть Ax. Все величины, в том числе Ax
от X не зависят. Задача считается
плоской 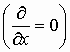 .
Найдем значения вектор-потенциала в каждом
слое. Вектор-потенциалы в каждом слое
должны удовлетворять следующему волновому
уравнению:
.
Найдем значения вектор-потенциала в каждом
слое. Вектор-потенциалы в каждом слое
должны удовлетворять следующему волновому
уравнению:
где ![]()
![]()
Решение уравнения (1) известно [1], поэтому запишем сразу выражения для вектор-потенциала в каждом слое в виде несобственных интегралов
Здесь ![]() - периодические функции
- периодические функции ![]() . Характеристические числа
. Характеристические числа ![]() имеют спектр значений от 0 до
имеют спектр значений от 0 до ![]() . Чтобы интегралы были сходящимися,
полагают
. Чтобы интегралы были сходящимися,
полагают ![]() .
Для определения неизвестных функций
.
Для определения неизвестных функций ![]() воспользуемся граничными условиями задачи
воспользуемся граничными условиями задачи
Удовлетворяя
граничным условиям, получим систему
уравнений для определения функций ![]() .
После этого можно записать выражения для
вектор-потенциала линейного тока в каждом
слое:
.
После этого можно записать выражения для
вектор-потенциала линейного тока в каждом
слое:
при ![]() (9)
(9)
В формуле (9) показатель экспоненты последнего члена в фигурных скобках берется со знаком "плюс" для области
получаем
(14)
где
Знак "минус" в формулах (14)-(15) для области
2. Решение методом криволинейных координат
.Для получения приближенных выражений для составляющих поля воспользуемся методом криволинейных координат [З], сущность которого заключается в следующем.
Пусть бесконечно длинный линейный переменный ток расположен в нижнем слое трехслойного бесконечно - длинного цилиндра параллельно образующей этого цилиндра. Зависимость от времени линейного тока зададим в виде
где
где
где
асимптотические формулы для функций Бесселя. Ограничиваясь формулами первого приближения, запишем
так как величина ![]() достаточно велика, то
достаточно велика, то
На основании формул (21)-(24),
опуская громоздкие промежуточные выкладки,
выпишем сразу выражения для интересующих
нас коэффициентов ![]() и
и ![]() ,
замечая, что зависимость по n исчезла.
,
замечая, что зависимость по n исчезла.
где 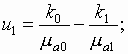
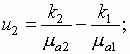
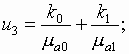
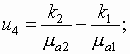
![]() -
толщина слоя,
-
толщина слоя, ![]() .
.
Положим ![]()
![]()
![]() .
.
Подставим выражения (25)
и (26) для коэффициентов ![]() и
и ![]() в
формулы (17) и (20),
получим после ряда преобразований
следующие приближенные выражения
в
формулы (17) и (20),
получим после ряда преобразований
следующие приближенные выражения
Тангенциальная и радиальная составляющие напряженности магнитного поля в каждом слое определяется по формулам:
Таким образом, приближенные выражения для горизонтальной и вертикальной составляющих вектора напряженности магнитного поля переменного тока в верхней среде, которую считаем воздухом, после несложных преобразований выражения будут иметь следующий вид:
Погрешность полученных приближенных решений определяется тем, что при суммировании рядов мы ограничиваемся главной частью разложения в асимптотических формулах для модифицированных функций Бесселя при больших аргументах. Конечные выражения не содержат интегралов и рядов, поэтому весьма удобны для вычислений. Кроме того, они могут использоваться как основа для получения приближенных решений более сложных дифракционных задач. Поэтому, представляется важным оценить область применимости приближенного решения, что может быть выполнено путем численного сравнения со строгим решением.
3. Численные исследования влияния электрических параметров слоев, частоты и границ раздела на структуру поля линейного переменного тока.
Результаты расчетов приведены на рис. 3 - 7. В обозначениях составляющих на графиках опущены индексы слоя, так как везде в работе исследуются компоненты магнитного поля линейного тока в воздухе. Заметим, что штриховые кривые относятся к приближенному расчету, а сплошные - к точному. Вид кривых на всех рисунках характеризует структуру поля при перемещении точки наблюдения в плоскости перпендикулярной оси линейного тока.
Рассмотрим случай с
одной границей раздела. Из рис.3
видно, что максимальное значение модуля
вертикальной компоненты составляет
несколько больше половины составляющей
величины ![]() ,
как для приближенного, так и для строгого
решения. Точка пересечения
,
как для приближенного, так и для строгого
решения. Точка пересечения ![]() и
и ![]() несколько смещена по оси абсцисс от единицы
к центру. Указанные свойства более ярко
выражены для приближенного решения и
характеризует влияние границы раздела. Из
приведенного рисунка видно, что
амплитудное значение строгого и
приближенного решения весьма сильно
отличаются.
несколько смещена по оси абсцисс от единицы
к центру. Указанные свойства более ярко
выражены для приближенного решения и
характеризует влияние границы раздела. Из
приведенного рисунка видно, что
амплитудное значение строгого и
приближенного решения весьма сильно
отличаются.
Значения фазы вертикальной составляющей для строгого и приближенного решений весьма близки. При переходе через "нуль" происходит скачок фазы на p , далее фаза незначительно изменяется с расстоянием. Фаза горизонтальной составляющей плавно меняется с удалением от центра, причем, в приближенном решении - более резко.
Перейдем к рассмотрению
составляющих поля для слоистой модели
среды. Поведение фазы и модуля
горизонтальной компоненты показано на рис.
4. С увеличением проводимости слоев
величина ![]() уменьшается и происходит более сильная
деформация кривых, т.е. более четко
проявляются боковые минимумы и максимумы, и
происходит их смещение к центру. Эти
явления характерны для обоих решений. По
абсолютной величине наблюдается различие.
Поведение фазы горизонтальной компоненты
при изменении проводимости слоев для
приближенного решения довольно верно
выражает общие закономерности. Можно
отметить, что в приближенном решении
имеется более сильная зависимость от
проводимости слоев. Например, Фазовая
кривая (рис. 4, кривая 1)
приближенного решения почти совпадает с
кривой (рис. 4, кривая 2) точного
решения для более проводящих слоев.
уменьшается и происходит более сильная
деформация кривых, т.е. более четко
проявляются боковые минимумы и максимумы, и
происходит их смещение к центру. Эти
явления характерны для обоих решений. По
абсолютной величине наблюдается различие.
Поведение фазы горизонтальной компоненты
при изменении проводимости слоев для
приближенного решения довольно верно
выражает общие закономерности. Можно
отметить, что в приближенном решении
имеется более сильная зависимость от
проводимости слоев. Например, Фазовая
кривая (рис. 4, кривая 1)
приближенного решения почти совпадает с
кривой (рис. 4, кривая 2) точного
решения для более проводящих слоев.
Как видно из рис.5,
максимум ![]() с увеличением проводимости смещается к
центру. По амплитуде приближенные значения
с увеличением проводимости смещается к
центру. По амплитуде приближенные значения ![]() значительно превосходят точные.
значительно превосходят точные.
Фазовые характеристики
приближенного и строгого решения наиболее
сильно отличаются с увеличением
проводимости слоев (рис. 5, кривые
1, 2). При достаточном удалении от начала
координат наблюдается их расхождение.
Рассмотрим поведение составляющих для
различных значений частоты сигнала. С
ростом частоты величина ![]() уменьшается, и максимумы смещаются к центру
(рис.6). Отметим, что при данной
проводимости слоев амплитуды и фазы
уменьшается, и максимумы смещаются к центру
(рис.6). Отметим, что при данной
проводимости слоев амплитуды и фазы ![]() для двух решений отличаются незначительно.
Здесь покрывающий слой имеет более высокую
проводимость, чем нижний слой
для двух решений отличаются незначительно.
Здесь покрывающий слой имеет более высокую
проводимость, чем нижний слой ![]() .
Кривые, построенные по точным формулам,
имеют максимумы ближе к центру, чем кривые
приближенного решения. Если сравнить
кривые 1 (рис.6) и кривые 2 (рис.5)
.
Кривые, построенные по точным формулам,
имеют максимумы ближе к центру, чем кривые
приближенного решения. Если сравнить
кривые 1 (рис.6) и кривые 2 (рис.5)
![]() то
можно заметить, что амплитуда
то
можно заметить, что амплитуда ![]() для приближенного решения сильно
уменьшается, когда верхний слой более
проводящий, в то время как амплитуда
для приближенного решения сильно
уменьшается, когда верхний слой более
проводящий, в то время как амплитуда ![]() для точного решения несколько возросла. То
есть, приближенное решение дает неверную
оценку явлений, происходящих при сравнении
случаев
для точного решения несколько возросла. То
есть, приближенное решение дает неверную
оценку явлений, происходящих при сравнении
случаев ![]() и
и
![]() .
.
Из рис.7 видно,
что с ростом частоты амплитуды ![]() уменьшаются, а минимумы и малые максимумы
смещаются к центру, при этом амплитуды
точного решения превосходят величины
уменьшаются, а минимумы и малые максимумы
смещаются к центру, при этом амплитуды
точного решения превосходят величины ![]() приближенного решения. Фазовые
характеристики составляющих довольно
плавно изменяются по мере удаления от
центра. С ростом частоты фазовые
характеристики изменяются более сильно. В
общем, частотная зависимость составляющих
достаточно верно отражается приближенным
решением.
приближенного решения. Фазовые
характеристики составляющих довольно
плавно изменяются по мере удаления от
центра. С ростом частоты фазовые
характеристики изменяются более сильно. В
общем, частотная зависимость составляющих
достаточно верно отражается приближенным
решением.
Выводы
1. Приведено строгое и приближенное решение задачи об излучении линейного переменного тока в плоскослоистой среде.
2. В результате численного анализа по точным и приближенным формулам отмечены некоторые особенности поведения компонент поля в диапазоне длинных и средних волн.
3. При расчетах по приближенным формулам более чем на порядок уменьшаются затраты машинного времени по сравнению с расчетами по точным интегральным выражениям.
4. В результате оценки области применимости приближенного решения показано, что оно пригодно для оценки общих закономерностей поведения составляющих поля в плоскослоистой среде при изменении электрических параметров слоев и частоты.
5. Показано, что наличие границ раздела слоев, увеличение проводимости среды и частоты существенно влияет на структуру электромагнитного поля тока.
Литература
1.Бурсиан В.Р. Теория электромагнитных полей, применяемых в электроразведке. Изд.2-е Л., "Недра", 1972.
2. Забаровский А.И. Переменные электромагнитные поля в электроразведке. Изд. МГУ, 1960.
3.Кулько В.А. Михайловский В.Н. Электромагнитное поле в слоистых проводящих средах. Киев, "Наукова думка", 1967.
4.Великий А.Б. Франтов Г.С. Электромагнитные поля, применяемые в индукционных методах электроразведки. М., Гостоптехиздат, 1962.
Рис.1. Геометрия задачи
Рис.2. Геометрия задачи
Относительное расстояние
y/hРис.3 Поведение
вертикальной и горизонтальной
составляющих магнитного поля линейного
переменного тока с изменением расстояния
Относительное расстояние
y/hРис.4. Влияние
электрических параметров слоев на
поведение
горизонтальной составляющей магнитного
поля.
Относительное расстояние
y/hРис.5 Влияние
электрических параметров слоев на
поведение
вертикальной составляющей магнитного поля.
Рис.6. Поведение модуля и
фазы вертикальной составляющей магнитного
поля с изменением частоты
1 – f = 0.3 МГц
2 – f = 0.5 МГц
Рис.7. Поведение модуля и фазы горизонтальной составляющей с изменением частоты.
1 –
f = 0.3 МГц
2 – f = 0.5 МГц