| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" №6, 2007 |
УДК 538.566.2:621.372.8
О сверхфокусировке плОСКой линзы
из отрицательного материала
В.В.Шевченко
Институт радиотехники и электроники РАН
Получена 19 июня 2007 г.
Показано, что бесконечная плоская линза из материала с отрицательными значениями диэлектрической и магнитной проницаемостей, равных по величине проницаемостям внешней среды, но отличающихся по знаку, переводит поле точечного источника в точечное изображение независимо от длины волны излучения.
Введение
Плоская (с плоскими границами) линза из материала с отрицательными диэлектрической и магнитной проницаемостями, в частности, с равными по величине и разными по знаку по отношению к проницаемостям внешней среды, впервые была рассмотрена в работе [1], где дана геометрооптическая теория такой линзы. В статье [2] было заявлено, что такая линза обладает свойством сверхразрешения малых объектов, то есть способностью различать изображения объектов, размеры которых и расстояния между которыми меньше длины волны излучения. Однако изложенная в [2] волновая теория плоской линзы неудовлетворительна ни с математической, ни с физической точек зрения. Используемые в ней для описания волнового поля внутри линзы суммы плоских волн (фактически несобственные интегралы) являются расходящимися, поэтому из полученного там (странным образом, см. ниже) результата о возрастании поля парциальных плоских волн внутри линзы нельзя сделать какие-либо определенные выводы о полном поле, представленном в виде разложения по плоским волнам, например, вывод о возрастании полного поля по толщине линзы. Приведенное же описание физического процесса прохождения волнового поля через линзу на основании существенного отражения плоских волн от границ линзы и по этой причине возрастания их поля противоречит тому, что на самом деле для рассматриваемого случая сред без потерь при одинаковых по величине и разных по знаку проницаемостях линзы и внешней среды отражение волн от границ линзы (от каждой границы) отсутствует (см. [3] и ниже в данной статье). Таким образом, процесс прохождения волн через линзу описан в [2] неверно, и из представленной там теории не следует выдвинутое утверждение о сверхразрешении такой плоской линзы.
С другой стороны, если показать, что рассматриваемая плоская линза обладает свойством сверхфокусировки, то есть если она переводит поле точечного источника в точечное изображение при любой длине волны излучения, то из этого результата будет однозначно следовать указанное свойство сверхразрешения линзы. В связи со сказанным в данной работе проведено детальное рассмотрение процесса прохождения сферических волн через плоскую линзу с целью обоснования свойства сверхфокусировки такой линзы.
1. Плоская линза и сферические волны
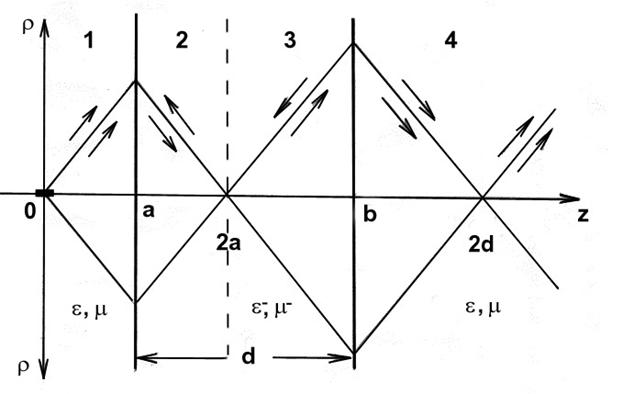
На рис.1 представлено лучевое описание процесса прохождения через плоскую линзу поля, излученного точечным источником [1]. Верхними стрелками показано направление фазовой скорости лучей (плоских волн) из пучка, излученного источником, а нижними – направление потока энергии (мощности). Из геометрооптических соображений следует, что линза действует в режиме фокусировки лучей только при выполнении условия a < d, а при a > d она оказывается рассеивающей лучи, где а – расстояние от источника поля до линзы, d – толщина линзы. При этом в режиме фокусировки расстояние между источником и его изображением равно 2d (рис.1).
Рис.1. Плоская линза: b – a = d, d – толщина линзы, e- = -e*, m- = -m*.
Что касается волнового описания поля, то естественно ожидать, что при наличии фокусировки в процессе прохождения сферических волн через границы линзы в каждой из указанных на рис.1 областей поле может быть представлено в виде расходящихся (в 1 и 3) и сходящихся (в 2 и 4) сферических прямых (в 1 и 4) и обратных (в 2 и 3) волн [4, 5]:
С1
exp(-ikr1), С2
ехр(ik-r2),
С3
ехр(-ik-r3), С4
ехр(ikr4),
(1)
где опущен временной сомножитель ехр (iwt) и в цилиндрических координатах (рис.1)
r1 = (r2 + z2)1/2, r2 = [r2 + (2a – z)2]1/2,
r3 = [r2 + (z – 2a)2]1/2, r4 = [r2 + (2d – z)2]1/2,
(2)
r – поперечная, z – продольная координаты;
k = k0(em)1/2 = k’ + ik”, k’ > 0, k” < 0,
(3)
e = e’ + ie”, m = m’ + im”,
e’ > 0, e” < 0, m’ > 0, m” < 0,
(4)
k- = k0(e-m-)1/2 = -k*,
e- = -e*, m- = -m*,
(5)
k0 = w/c, w – круговая частота, с – скорость света. Здесь, как обычно, при помощи малых мнимых частей указанных величин учтены потери энергии из-за диссипации и поглощения волн в среде, а звездочкой обозначены комплексно-сопряженные значения. Ясно, что приведенное представление волновых полей в виде (1) в указанных на рис.1 областях справедливо, если отражение волн от границ линзы отсутствует совсем или если оно мало и им можно пренебречь. При этом отметим, что отраженные от границ волны, если они возникают, оказываются расходящимися в плоскости линзы, и они не фокусируются в линзе на и вблизи оси z, на которой расположены источник поля и его изображение.
2. Граница между положительной и отрицательной средами
Рассмотрим здесь случай, когда потери волн в средах отсутствуют:
e* = e’ = e, m* = m’ = m,
k* = k’ = k > 0.
(6)
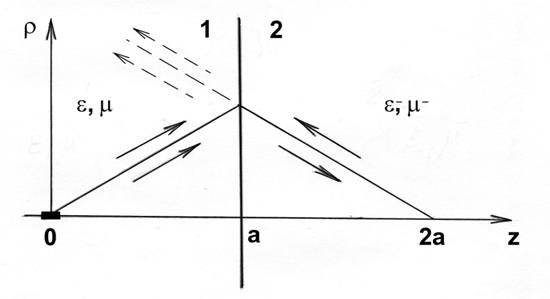
Рис.2. Граница между положительной и отрицательной средами.
Учет потерь требует специального рассмотрения. Исследуем прохождение сферической волны, возбужденной точечным источником, через плоскую границу между положительной (e, m > 0) и отрицательной (e-, m- < 0) средами при e- = -e, m- = -m, k- = -k. Пусть поле в точке r = 0, z = 0 возбуждается точечным электрическим диполем, дипольный момент которого направлен вдоль оси z (рис.2). Тогда соответствующая компонента вектора Герца излученного поля может быть представлена в области 1 в виде
,
(7)
где С1 – константа, пропорциональная дипольному моменту, J0(cr) – функция Бесселя,
g = (k2 -c2)1/2 = g’ + ig”, g’ > 0, g” < 0.
(8)
При вещественном k имеем g’ > 0, g” = 0, если c < k, и g’ = 0, g” < 0, если c > k. Сферическая волна в (7) представлена согласно спектральной теории открытых волноведущих структур [6, 7] в виде спектрального разложения по плоско-цилиндрическим (волноводным) собственным волнам. Положив в (7) z = 0 и используя свойство ортогональности собственных (цилиндрических) функций
(9)
получим [8]
.
(10)
Для прямой расходящейся сферической волны полученный результат хорошо известен [9, 10]. Этим же методом спектрального разложения будем искать поле сходящейся обратной волны в области 2 в виде
,
(11)
где Т(c) – искомый коэффициент прохождения волнового поля через границу z = а, F2(c) = ig-1. Аналогично представим отраженное от границы z = а поле прямой расходящейся волны в области 1 в виде
,
(12)
где R(c) – коэффициент отражения, FR(c) = ig-1.
Следует отметить, что при c > k согласно (8) имеем
g = -i |c2 – k2| 1/2 = ig”, g” < 0,
(13)
поэтому соответствующие экспоненциальные множители у парциальных собственных волн под интегралами в (7) и (12) являются спадающими для падающей на границу z = a волны при возрастании z в области 1, а для отраженной волны – при уменьшении z в области 1. Под интегралом же в (11) для прошедшей волны такой множитель оказывается возрастающим при увеличении z в области 2. В связи с этим важно особо подчеркнуть, что здесь мнимые значения g связаны не с потерями или с увеличением энергии поля волн в среде, поскольку k является вещественной величиной, и не с тем, положительная это среда или отрицательная, то есть не со свойствами среды. Мнимые значения g не отражают здесь способность среды ослаблять или усиливать волны, как это ошибочно утверждается в работе [2] и на этом строится неправильная интерпретация физического процесса прохождения волн через рассматриваемую линзу, они отражают структурные свойства поля сферической волны. Спадание экспонент в (7), (12) связано с процессом спадания поля у расходящихся сферических волн при удалении от источника, а возрастание экспонент в (11) – с процессом возрастания поля при его концентрации вблизи оси z у сходящейся сферической волны,сфокусированной в данном случае границей между средами, в области 2 при z ® 2а. Ниже это подтверждается. В то же время в математическом плане все несобственные интегралы в (7), (11), (12) являются здесь сходящимися соответственно при 0 < z £ a, a £ z < 2a, z £ a, то есть в областях их применения они описывают конечные по величине поля.
Чтобы рассчитать процесс прохождения волн через границу z = a, необходимо «сшить» поля на этой границе согласно условиям
Er1 - ErR = Er2, Hj1 + HjR = Hj2,
(14)
где
Er =
, Hj = -ik0e
.
(15)
На основании (15), используя спектральное представление компоненты вектора Герца (7), для падающего поля получим
Er1 = C1
(cr)exp(-igz)c2dc,
Hj1 = k0eC1
(cr) exp(-igz)c2dc,
(16)
где учтено, что dJ0(cr) / dr = -cJ1(cr) [8]. Аналогично на основании (11), (12), (15) вычисляются компоненты Еr2, ЕrR, Hj2, HjR для прошедшего и отраженного полей. Подставив полученные выражения в граничные условия (14), умножив обе части равенств на rJ1(cr) и проинтегрировав их по r от 0 до ¥ [6, 7], с учетом свойства ортогональности
(cr)J1(
r)rdr = c-1d(c -
)
(17)
получим систему уравнений
1 – R(c) = T(c), e[1 + R(c)] = -e-T(c).
(18)
Поскольку e- = -e, то решение этой системы имеет вид
T(c) = 1, R(c) = 0.
(19)
Отсюда следует. что отражение от границы z = a отсутствует, а функция поля прошедшей волны согласно спектральному представлению (11) может быть свернута, аналогично (7), к виду
Pz2 = C1r2-1exp(ik-r2),
(20)
где k- = -k и, как в (2), r2 = [r2 + (2a – z)2]1/2, то есть прошедшая волна является сходящейся обратной сферической волной. Таким образом, при r2 = 0 или, что то же самое, в точке r = 0, z = 2а (рис.2) имеет место точечное изображение источника поля.
Аналогичное рассмотрение прохождения волн через вторую границу линзы приводит к такому же результату, при этом амплитудные коэффициенты в выражениях (1) в случае среды без потерь оказываются связанными равенствами: С2 = С3 = С4 = С1.
Заключение
Проведенное рассмотрение процесса прохождения сферических волн через плоскую линзу из отрицательного материала с проницаемостями e-, m- < 0 показало, что такая линза при e- = -e, m- = -m, где e и m - параметры внешней среды, обладает свойством сверхфокусировки, то есть она переводит поле точечного источника в точечное изображение независимо от длины волны излучения. Этот вывод, однако, сделан для модели линзы бесконечных размеров (с бесконечной плоской апертурой) и без учета потерь волн в материале линзы.
Список литературы
1. Веселаго В.Г. Успехи физич.наук. 1967. Т.92. № 3. С.517.
2. Pendry I.B. Phys. Rev. Lett. 2000. V.85. № 18. P.3966.
3. Шевченко В.В. Радиотехн. и электрон. 2004. Т.49. № 6. С.683. № 9. С 1048.
4. Шевченко В.В. Радиотехн. и электрон. 2003. Т.48. № 10. С.1202.
5. Шевченко В.В. Успехи физич.наук. 2007. Т.177. № 3. С.301.
6. Шевченко В.В. Плавные переходы в открытых волноводах. М.: Наука, 1969.
7. Шевченко В.В. Метод спектрального разложения полей в теории открытых волноводов. Диссертация … д-ра физ.-мат. наук. М.: ИРЭ АН СССР. 1976.
8. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: ГИФМЛ, 1962.
9. Каценеленбаум Б.З. Высокочастотная электродинамика. М.: Наука, 1966.
10. Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн. М.: Наука, 1979.