О расчете поля в области фокуса идеальной линзы Веселаго конечных размеров

"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" №6, 2007

О расчете поля в области фокуса идеальной

линзы Веселаго конечных размеров

А.П. Анютин
Российский Новый Университет, Москва

Получена 22 июня 2007 г.

Приводятся и обсуждаются результаты строгого численного решения двухмерной задачи рассеяния поля цилиндрической волны идеальной линзой Веселаго конечных размеров, а так же результаты расчетов продольной и поперечной структуры поля в области фокуса такой линзы. Показана конечность разрешения такой линзы. Отмечено, что поведение поля в области фокуса во многом аналогично случаю фокусировки сходящегося цилиндрического фронта волны. Установлено, что малые потери среды () почти не сказываются на разрешающей способности линзы, однако могу приводить к значительному изменению амплитуты поля на поверхности линзы

1. ВВЕДЕНИЕ

        В последнее время наблюдается значительный интерес к эффектам, возникающим при взаимодействии электромагнитных волн со средой, относительная диэлектрическая и магнитная проницаемости которой одновременно являются отрицательными величинами (). Такую среду принято называть средой с отрицательной рефракцией (метаматериалом, средой Веселаго), поскольку впервые задача распространения электромагнитных волн в среде с была достаточно подробно теоретически рассмотрена В.Веселаго еще в 1968 г. [1]. В этой работе он исследовал прохождение плоской гармонической волны через плоский слой среды с конечной толщины . При этом, исходя из анализа лучей геометрической оптики (ГО), соответствующей прохождению волны через пластину, В.Веселаго сделал ряд предсказаний относительно поля волны, прошедшей через слой. В частности, было указано на то, что слой среды с позволяет осуществить идеальную (с позиций ГО) фокусировку преломленных и прошедших ГО лучей (когда все ГО лучи сходятся в одной точке). Другими словами, слой такой среды преобразует расходящийся цилиндрический фронт падающей волны в сходящийся цилиндрический фронт прошедшей волны. Такой случай получил название идеальной линзы Веселаго.

      Число публикаций, посвященных теоретическому и экспериментальному исследованию этой проблемы к настоящему времени весьма велико (см. [2-8] и цитируемую там литературу) Отметим, что во всех теоретических работах используется модель слоя среды конечной толщины с бесконечными границами. При этом полученные решения базируются либо на представлении прошедшего поля в виде интеграла по плоским волнам, либо на лучевом описании поля в малоугловом приближении, либо на лучевом приближении, учитывающем однократное прохождение ГО лучей через слой, либо на использовании приближения Кирхгофа.

       В реальных экспериментах мы имеем дело с линзой конечных размеров, как в продольном, так и поперечном направлениях. Перенесение отмеченных выше методов на случай линзы конечных размеров затруднено тем, что представление решения в виде интеграла по плоским волнам здесь не работает, а для использования асимптотических методов необходимо знать достаточно точное распределение поля на выходе из пластины конечного размера. Однако для углов такой диэлектрической пластины не известны дифракционные коэффициенты. Кроме того, для нахождения распределения поля на всех четырех гранях пластины необходимо суммировать бесконечный ряд полей, обусловленный многократными отражениями полей на всех гранях пластины и т.п.

      В данной работе мы приводим результаты строгого численного решения двухмерной задачи рассеяния поля цилиндрической волны идеальной линзой Веселаго конечных размеров, а так же результаты расчетов продольной и поперечной структуры поля в области фокуса такой линзы. При этом учитывается не только конечность размеров линзы, но и потери среды.

2. Постановка задачи и обсуждение результатов расчетов

      Рассмотрим задачу рассеяния цилиндрической Е поляризованной волны :

                                        (1)

диэлектрической пластиной (линзой), форма поперечного сечения которой описывается уравнением:

                                                   (2)

и при значения параметра (см. Рис.1, Рис. 2) близка к прямоугольной. Считается, что среда пластины имеет относительную диэлектрическую проницаемость и относительную магнитную проницаемость , т.е. представляет собой среду В.Веселаго с показателем преломления (где величина - характеризует потери среды). Входящие в выражения (1), (2) величины представляют собой: {} – пространственные координаты точки наблюдения в цилиндрической системе координат; {} - пространственные координаты точки источника волны (нить магнитного тока) в цилиндрической системе координат; - характеризуют геометрию пластины ( - ее высоту, - ее ширину); - волновое число вакуума (свободного пространства), соответственно.

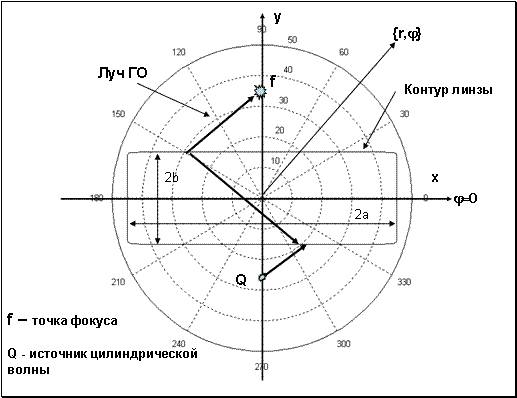
Рис.1 Геометрия задачи .

         Представим полное поле вне пластины (2) в виде суперпозиции поля падающей волны (1) и рассеянного поля :

          = + ,      (3)



а поле внутри пластины (2) обозначим .

          Как известно, поля и должны удовлетворять уравнениям Гельмгольца вне и внутри пластины соответственно, а также граничным условиям на контуре пластины, заключающимся в непрерывности полей и непрерывности их нормальных производных на контуре , т.е. являться решением граничной задачи.

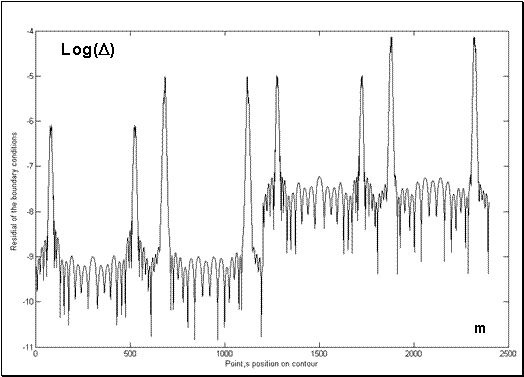
        Решение такой граничной задачи мы будем строить на основе модифицированного метода дискретных источников (ММДИ) [12-14], который позволяет получить численное решение граничной задачи с контролируемой точностью. Используемое в этом методе представление для полей , в виде суперпозиции полей вспомогательных цилиндрических источников, расположенных на вспомогательных поверхностях внутри и вне поверхности пластины [12] заведомо удовлетворяет уравнениям Гельмгольца. Амплитудные коэффициенты для полей вспомогательных цилиндрических источников в методе ММДИ находятся из граничных условий. При этом точность решения задачи определяется величиной невязки граничных условий. Поэтому мы контролировали невязку граничных условий в точках, расположенных в середине между точками, где граничные условия выполняются точно (в таких точках граничные условия выполняются наихудшим образом). Поскольку метод ММДИ и техника его применение к ряду задач рассеяния волн ограниченными телами описан достаточно подробно в работах [12-14], то мы не будем обсуждать особенности его применения в рассматриваемом случае, а лишь приведем на Рис.3 типичный для наших расчетов график распределения невязки граничных условий вдоль контура пластины . При этом значения представляют собой текущий номер точки контура; для точек график соответствует невязке полей, а для - невязке нормальных производных полей; - общее число вспомогательных источников.

Рис.2 Невязка краевых условий при ; N=1200; .

      Из рисунка Рис.2 видно, что максимальная невязка не превышает величины даже для “угловых” точек контура и что позволяет считать приведенные ниже результаты достаточно точными (по крайней мере, дальнейшее увеличение общего числа вспомогательных источников не приводит к каким либо видимым изменениям в поведении рассчитанных характеристик и лишь еще больше уменьшает невязку краевых условий, делая ее соизмеримой с величиной ).

      Обсудим теперь результаты численных расчетов диаграмм рассеяния и, распределения поля вдоль (т.е. при ) и поперек (т.е. при ) оси линзы Веселаго при различных значениях параметров, определяющих ее “электрическую” толщину   и “электрическую” высоту , потерях диэлектрика и положения источника волны {}.

         Рассмотрим сначала случай, когда для среды линзы выполняется условие . Геометрия линзы определялась значениями , . Источник волны имел координаты : {} (см. Рис.1). Согласно предсказанию Веселаго цилиндрическая волна после прохождения пластины должна сфокусироваться в точке с координатами в цилиндрической системе координат или в точке с координатами в декартовой системе координат (см. Рис.1).

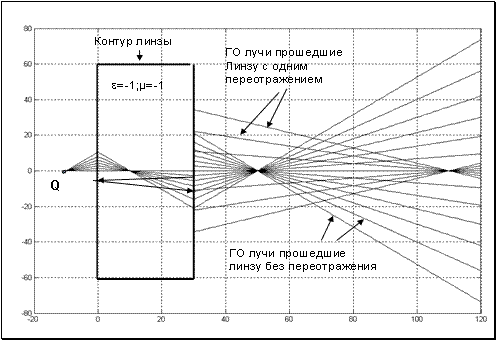
Рис.3 Лучевая картина прошедших ГО лучей через линзу В.Веселаго

       Отметим, что с точки зрения геометрической оптики (ГО) эта точка соответствует точке пересечения ГО лучей прошедших линзу без переотражения (см. Рис.3). Если учесть однократные переотражения на передней и задней гранях линзы, то появится еще одна точка фокусировки. Эта ситуация также изображена на Рис.3, где приведены соответствующие два семейства прошедших через линзу ГО лучей. Ясно, что последующие переотражения будут приводить к образованию все новых и новых фокальных точек. Таким образом положение первого фокуса, определяемое из формулы Веселаго [1] :



                                                                    (4)

соответствует идеальной фокусировке ГО лучей прошедших через линзу без переотражения на гранях линзы. Другими словами, линза Веселаго в таком и только таком приближении осуществляет преобразование расходящегося цилиндрического фронта падающей волны в сходящийся фронт волны прошедшей за линзу. Здесь следует сделать несколько комментарий к такому подходу.

      Хорошо известно, что с позиций ГО лучи не “знают” о том, как они образовались, и подчиняются только обычным законам ГО. Напомним, что случай идеальной фокусировки ГО лучей, т.е. когда все ГО лучи сходящегося фронта волны пересекаются в одной точке, имеет место в фазированных антенных решетках (ФАР) и подробно исследовался как в приближении Кирхгофа так асимптотической постановке [9-11] еще в 80-х годах прошлого века. При этом не было обнаружено сверхразрешения ФАР при фокусировке поля ФАР в ее ближней, промежуточной или дальней зонах. Применительно к нашей задаче следует указать и на то, что непосредственное перенесение методов и результатов этих работ на случай линзы Веселаго конечных размеров затруднено, поскольку представление для поля в виде интеграла по плоским волнам здесь применить не удается. Кроме того, не известно достаточно точное распределение поля на выходе из пластины конечного размера. Как известно, в таком случае не известны дифракционные коэффициенты для углов диэлектрической пластины, а для нахождения распределения поля на гранях пластины необходимо суммировать бесконечный ряд полей, обусловленных многократными отражениями полей на всех четырех гранях пластины и т.п. В свою очередь, это фактически так же делает затруднительным и применение приближения Кирхгофа к подобным задачам.

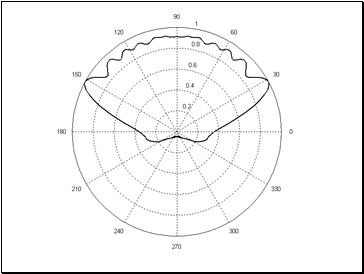
       На Рис.4а (Рис. 4б )представлены результаты расчетов не нормированной (нормированной)диаграммы рассеяния в прямоугольной системе координат (полярной системе координат) для показателя преломления среды и различных потерь среды , , и . Геометрия линзы характеризовалась следующими параметрами: , а источник падающей волны имел координаты: . Из рисунка следует, при изменении потерь диаграммы рассеяния мало отличаются друг от друга, и отличия в амплитудах начинает сказываться лишь при . При величине потерь осцилляции амплитуды практически исчезают. Отметим, что во всех случаях уровень поля рассеянного назад (т.е. поля в окрестности углов   ) существенно меньше уровня поля прошедшего вперед. Причем с ростом потерь среды уровень поля рассеянного назад уменьшается.



Рис. 4а Диаграмма рассеяния линзой Веселаго при различных потерях среды.




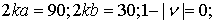
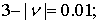
Рис. 4б Диаграмма рассеяния линзой Веселаго; .

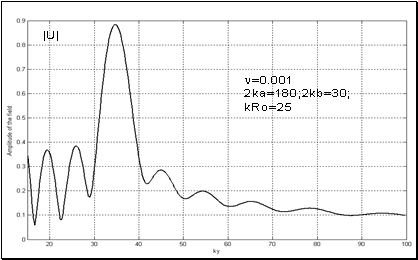
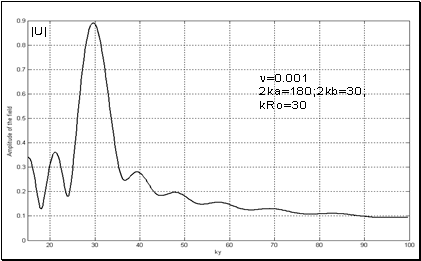
  Характер изменения полного поля вдоль оси линзы (начиная от ее стенки) при тех же самых параметрах линзы, потерь среды и положении источника иллюстрирует Рис.5. Из рисунка следует, что потери среды могут значительно изменить амплитуду поля на выходе из линзы. Поле за линзой представляет собой осциллирующую кривую, причем амплитуда колебаний поля за фокусом значительно меньше чем перед фокусом. Изменение потерь в диапазоне практически не сказывается на амплитуде поля в фокусе. При этом максимальное значение поля достигается в окрестности точки, координата которой дается формулой В.Веселаго (4) ( точнее, не в точке фокуса, а в точке смещенной от фокуса к границе линзы). Наличие осцилляций поля за линзой не связано с фокусировкой ГО лучей, испытавших разное число переотражений на гранях линзы, поскольку из Рис.3 следует, что ближайшая к фокусу точка следующей фокусировки должна располагаться в районе (в системе координат Рис.1).





Рис.5 Влияние потерь среды на распределение поля вдоль оси линзы Веселаго



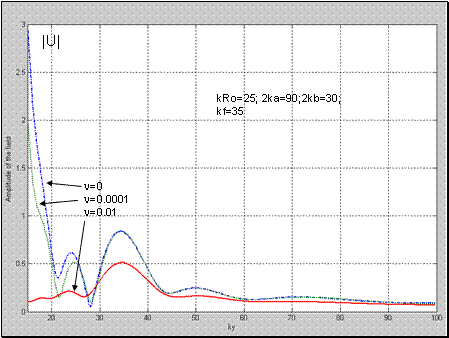
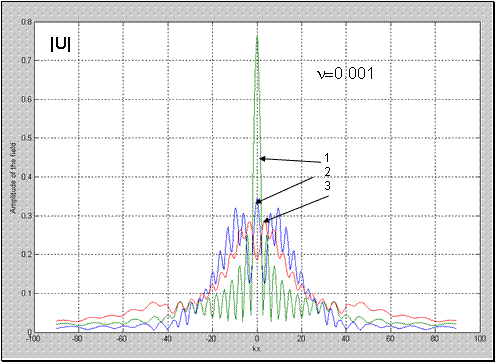
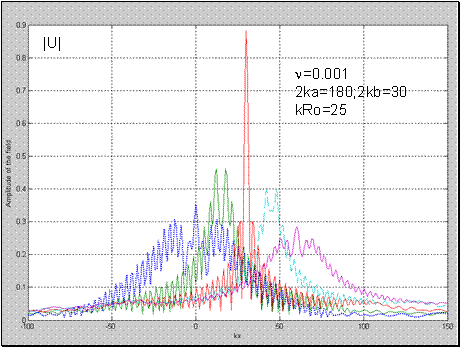
              Рис.6 – Рис.9 иллюстрируют поперечную структуру полного поля за линзой при различных потерях среды : , , , и при различных значениях продольной координаты (значения координаты представлены на рисунках). Линза имела геометрические размеры: источник цилиндрической волны располагался в точке с координатами: .

      Из рисунков видно, что поперечная структура поля представляет собой сложную осциллирующую кривую, причем характер ее изменения существенно зависит от положения точки относительно фокуса . Поле в фокусе имеет характерный вид кривой имеющей “лепестковую” структуру, у которой расстояние между минимумами главного лепестка , как известно, определяет разрешающую способность линзы. Отметим, что малые потери () не изменяют общей структуры поля (в том числе практически не сказываются на величине разрешающей способности ) и сказываются лишь на величине амплитуды осцилляций поля. Величина максимума в точке фокуса почти не меняется при лишь с значения уменьшает свое значение на 39%.

      Исследованию влияния увеличение геометрических размеров линзы ( например увеличение ее высоты в два раза ()) при неизменных остальных параметрах и удаление источника от линзы () посвящены результаты, представленные на Рис. 10 - Рис.12. Так, на Рис. 10 , Рис. 11 изображены

графики , показывающие изменение полного поля за линзой вдоль ее оси при

параметрах : , , а на Рис.12– изменение поперечной структуры полного поля при , соответственно (остальные параметры линзы, среды и источника не изменялись).


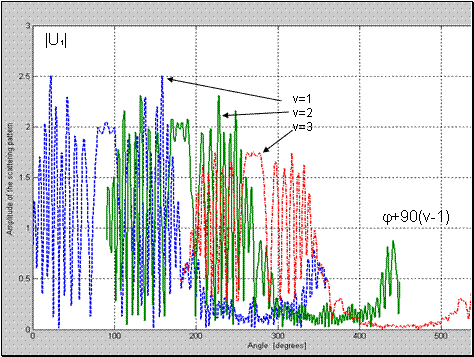
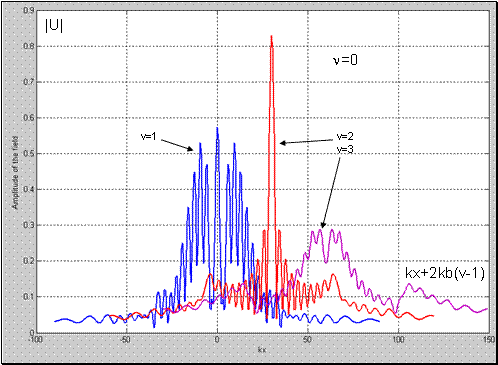
Рис. 6 Поперечное распределение поля прошедшего линзу;

                                     1 - ;     2 - ; 3 -


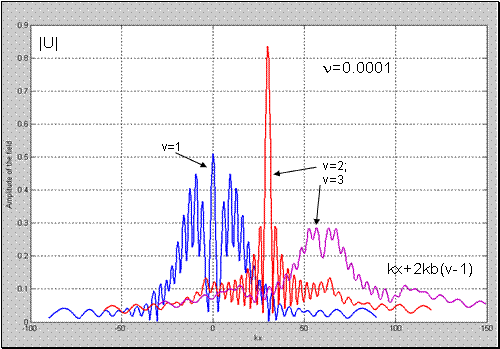
Рис. 7 Поперечное распределение поля прошедшего линзу;

                                     1 - ;     2 - ; 3 -


Рис.8 Поперечное распределение поля прошедшего линзу;

                                     1 - ;     2 - ; 3 -


Рис. 9 Поперечное распределение поля прошедшего линзу;

                       1 - ;     2 - ; 3 - ; ;

      Сравнивая результаты, приведенные на Рис. 10, с аналогичным результатом, приведенным на Рис.5, можно прийти к выводу о том, что увеличение высоты линзы в два раза (при одном и том же расположении источника волны и толщине линзы) приводит к появлению дополнительных осцилляций поля как в области между линзой и ее фокусом, так и в области за фокусом. Причем наблюдается увеличение амплитуды таких осцилляций. Расположение главного максимума приблизительно соответствует точке фокуса (сам максимум смещен в сторону границы линзы). Удаление источника волны вызывает смещение точки фокуса к границе линзы (как и предсказывает формула (4) Веселаго [1]) и уменьшению числа осцилляций в области между линзой и фокусом, что в рамках ГО объяснить нельзя.


Рис. 10 Продольное распределение поля за линзой Веселаго.



               Рис. 11 Продольное распределение поля за линзой Веселаго



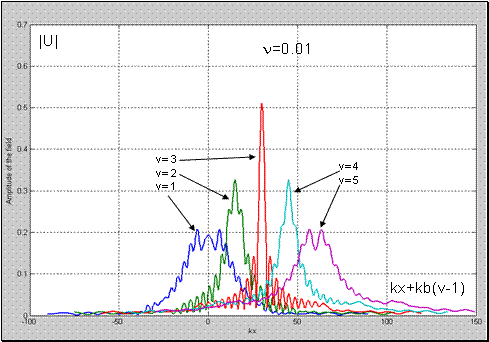
Графики пространственного поперечного распределения полного поля при различных значениях координаты для линзы с высотой иллюстрирует Рис. 12 . Отметим, что такое увеличение высоты линзы в два раза привело к увеличению наблюдаемых осцилляций поля. При этом, точке фокуса увеличение числа “лепестков” поперечной структуры поля не сопровождалось изменением расстояния между минимумами его главного лепестка (т.е. не изменило разрешающей способности линзы).


Рис. 12 Пространственное распределение поля вдоль оси линзы В.Веселаго

                       1 - ;     2 - ; 3 - ; ;

                                          ,.

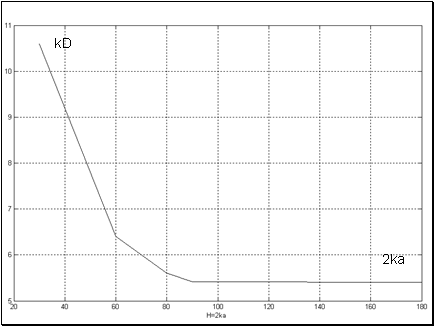
     Наконец, приведем результаты показывающее изменение расстояния между минимумами главного лепестка поля в фокусе линзы (разрешение линзы) при различных значениях высоты линзы . При расчетах полагалось: , , , . Из рисунка следует что увеличение высоты линзы сначала приводит к уменьшению значений разрешающей способности, а начиная с значений практически ее не изменяет.


Рис.13 Влияние высоты линзы на ее разрешение

В заключении отметим, что представленные результаты позволяют сделать следующие выводы:

    - уровень рассеянного назад линзой поля существенно меньше уровня прошедшего поля и учет потерь ведет к еще большему уменьшению этого уровня,

     - формула В.Веселаго (4) [1] правильно указывает на координату точки, в районе которой расположении максимум сфокусированного линзой поля,

     - максимум сфокусированного поля смещен из фокуса линзы в сторону самой линзы,

     - малые потери не изменяют общего характера поля в окрестности фокуса и не сказываются на разрешающей способности линзы,

     - разрешающая способность конечной линзы ограничена и с изменением высоты линзы выходит на некоторое предельное значение,

- амплитуда поля на границе линзы существенно зависит от потерь среды и может превышать знамение амплитуды поля в фокусе линзы.

Автор выражает признательность В.А. Калошину за обсуждение результатов работы и полезные замечания.



Работа выполнена при поддержке Российского Фонда Фундаментальных исследований (гранты № 06-02-16804 и № 06-02-16483)

Литература

1. V.G. Veselago, "Тhe Electrodynamics of Substances with Simultaneously Nega-

tive Values of and ", Sov. Phys. Usp., vol. 10, рр. 509, 1968.

2. D.R. Smith et а/., "Composite Medium with Simultaneously Negative Permeability and Permittivity", Phys. Rev. Lett., vol. 84, р. 4184, 2000.

3. J.B. Pendry and D.R. Smith, "Reversing Light with Negative Refraction", Physics Today, June 2004, рр. 37, 2004.

4. J.B. Pendry, ''Negative Refraction Makes а Perfect Lens", Phys. Rev. Lett., vol. 85, рр. 3966, 2000.

5. GW. 't Hooft, "Comment оп ''Negative Refraction Makes а Perfect Lens"", Phys. Rev. Lett., vol. 87, рр. 249701.1, 2001.

6. George V. Eleftheriades, Ashwin К. Iyer and Peter С. Кremer, Planar Negative Refractive Index Media Using Periodically L-C Loaded Transmission Lines, IEEE Tr.MTT,vol.50,N 12, pp. 2702, December 2002

7.Шевченко В.В., Об обратных плоских волнах в однородных изотропных средах, РЭ, т.48, N 10, с. 1202, 2003.

8. Dorofeenko A.V., Lisyansky A.A., Merzlikin A.M.,Vinogradov A.P., Full-wave analysis of imaging by the Pendry-Ramakrishna stackable lens, Physical Review,B 73,235126 2006.

9. Кинбер Б.Е., Анютин А.П., Мартынов А.М., Специфика метода фокусировки при измерении диаграмм плоских фазированных антенных решеток, РЭ ,1982, т.27, N 6, с. 1120, 1982

10. Кинбер Б.Е., Новоселов С.В., Поле в окрестности фокуса, РЭ, т.30, N 8, с.1469, 1985.

11. ВагановР.Б.РЭ,1983,т.28, N 5, с.834.

12. A.P. Anioutine, A.G. Kyurkchan, S.A. Minaev, About universal modification to the method of discrete sources and its application, JQSRT, Vol. 79-80, pp.509, 2003

13. А.П. Анютин, А.Г. Кюркчан, С.А. Минаев, О новой модификации метода дискретных источников, Радиотехника и Электроника, т.47, N 6, c.688, 2002

14. A.P. Anioutine, A.G. Kyurkchan, S. A. Manenkov, S.A. Minaev, About 3D solution of diffraction problems by MMDS, JQSRT, v.100, N1-3, pp.26, 2006 (July/Augest).

xxx