УДК 517 + 530
АППРОКСИМАЦИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
ПРОВОДНИКОВ ПОЛЯМИ ЭКРАНИРОВАННЫХ ТОЧЕЧНЫХ ЗАРЯДОВ
В. П. Казанцев, М. В. Долгополова
Сибирский
федеральный университет
Получена
2 июня 2008 г.
Найдены комплексные электрические потенциалы и энергетические соотношения для экранированных точечных зарядов на плоскости. Показано, что, как комплексные электрические потенциалы экранированных точечных зарядов, так и их энергии взаимодействия могут быть выражены через функции Грина. Построена вариационная схема аппроксимации полей проводников полями экранированных точечных зарядов, эффективность которой подтверждается примерами расчета погонной емкости длинных линий.
В работе [1] дан подробный анализ понятий точечных мультиполей на плоскости, а также показано, что электрическое поле системы круговых параллельных проводов может быть на основе вариационного принципа Гаусса приближенно с какой угодно точностью полями точечных мультиполей отдельных проводов. В работах [2,3], где рассматривались задачи электростатики на плоскости, было указано, что с полем аппроксимирующего точечного заряда тесно связано понятие внутреннего конформного радиуса
, так что величину аналогичную определяемой в работе [4] емкости поверхности относительно точки, емкость линии относительно точки
можно определить как:
;
где
- нормировочная постоянная [3]. Если заменить электрическое поле экранированного проводника вне него полем экранированного точечного заряда, расположенного внутри проводника в точке
, то такой аппроксимации будет отвечать оценка снизу емкости проводника относительно экрана [2]
, (1)
где
и
- внутренние конформные радиусы полости экрана и области проводника относительно точки
;
и
- емкости проводника и экрана относительно точки
.
Естественным образом возникает вопрос о последовательном уточнении оценки (1). Такое уточнение можно проводить, приближая электрическое поле экранированного проводника полями экранированных точечных зарядов, расположенных в одной или нескольких точках внутри проводника. В связи с чем возникает потребность анализа потенциалов, напряженностей электрических полей и энергий экранированных точечных зарядов. Такой анализ и будет проведен в этой работе.
Электрические поля и энергии экранированных точечных зарядов
Подробный анализ комплексной функции Грина для областей комплексной плоскости проведен в работе [3]. Напомним, что комплексная функция Грина области представляет собой комплексный потенциал, в общем случае с точностью до постоянной величины, экранированного границей области единичного точечного заряда. Для конечной области комплексной плоскости
, она может быть выражена через функцию
, конформно отображающею экранированную область на круг радиусом
так, что
;
,
по формуле
. (2)
Положительную величину
называют внутренним конформным радиусом области, ассоциированным с точкой
. На экране, как это видно из (2),
.
Для анализа удобно представлять функцию Грина суммой
, (3)
где
- комплексный потенциал единичного точечного заряда (функция Грина всей комплексной плоскости). В этой работе
мы не будем отличать от комплексного потенциала зарядов
, наведенных на заземленном экране
электрическим полем точечного заряда, расположенного в точке
, поскольку будем рассматривать либо конечные экранируемые области, либо бесконечные экраны. Таким образом,
. (4)
Отметим, что вне экрана
, то есть совпадает с потенциалом отрицательного единичного точечного заряда, расположенного в точке
.
Для реализации вариационного подхода к задачам аппроксимации электрического поля проводников полями точечных зарядов важны энергетические соотношения. Собственная энергия зарядов, наведенных на экране полем точечного заряда
, расположенного в точке
равна
. (5)
Энергия взаимодействия наведенных зарядов с точечным зарядом выражается соотношением:
. (6)
Энергия взаимодействия двух точечных экранированных зарядов
и
, расположенных в различных точках
и
может быть выражена через функцию Грина
, (7)
поскольку
и
- это комплексные потенциалы, создаваемые единичными точечными зарядами, расположенные в точках
и
, в точках
и
. Заметим, что из полученного соотношения ясна видна симметрия реальной части функции Грина относительно перестановки
и
, а вместе с тем и гармоничность
, как по
так и по
.
Вариационная схема решения задачи аппроксимации электрического поля проводников полями экранированных точечных зарядов
Пусть провод, на комплексной плоскости которому соответствует область, заключен внутри параллельного ему цилиндрического экрана. Этому экрану на комплексной плоскости будет отнесена область
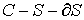
. Будем аппроксимировать поле вне провода в области
полями экранированных точечных зарядов, расположенных в точках
, источниками которых служат распределенные по
с плотностями
заряды.
Поле экранированного провода, которому на комплексной плоскости отвечает область
, аппроксимируем комплексным потенциалом [5]
,
который является вне провода суперпозицией потенциалов экранированных точечных зарядов
расположенных в точках
, а внутри провода суперпозицией потенциалов зарядов, наведенных точечным зарядом
на поверхности провода.
Собственная энергия экранированных точечных зарядов может быть записана в виде:
;
;
, (8)
где
и
;
и
- внутренние конформные радиусы и функции Грина областей
и
.
При решении задачи о емкости экранированного провода следует минимизировать функционал энергии (8) по
и
при условии постоянства полного заряда проводника
.
Минимизируя электростатическую энергию, получим
.
Для значения емкости провода относительно экрана, на основании вариационного принципа Гаусса [6] будем иметь неравенство:
. (9)
Рассмотрим теперь как реализуется предложенная вариационная схема на конкретном примере.
Комплексные функции Грина круга, кругового кольца, кругового полукольца и прямоугольника
Решение этой задачи может быть осуществлено по общей схеме, описанной формулами (8) – (9). Для этого найдем функцию Грина круга, она может быть выражена через функцию
,
конформно отображающую круг
на круг радиусом
,
тогда
Функция Грина для кругового кольца
будет иметь вид:
Функция Грина кругового концентрического полукольца
может быть выражена через комплексную функцию Грина кругового концентрического кольца
, если воспользоваться зеркальной симметрией кольца относительно оси
. В самом деле, функция
при
и
будет аналитической функцией
в полукольце, реальная часть которой принимает на отрезках оси
те же значения, что и
, а на границах
и
нулевые значения. Тогда комплексной функцией Грина для полукольца будет служить
,
и, используя формулу (11) можно найти
. (12)
Функция Грина для прямоугольника
может быть выражена через функцию Грина кругового концентрического полукольца (12) и функцию
;
,
которая конформно отображает прямоугольник
на полукольцо
. Используя эти формулы, получим функцию Грина
Рассмотрим выражение для внутреннего конформного радиуса прямоугольника, ассоциированного с точкой
:
, (14)
Используя формулу (14) и выражение для внутреннего конформного радиуса круга с радиусом
:
,
для диагональных элементов энергетической матрицы запишем
Для записи недиагональных элементов энергетической матрицы согласно соотношению (8) следует использовать комплексные функции Грина прямоугольника (13) и круга (10), тогда
Аппроксимация электрического поля заряженного проводящего круга, экранированного в прямоугольнике полями экранированных зарядов
Будем аппроксимировать электрическое поле экранированного в прямоугольнике круга полями пяти экранированных точечных зарядов
,
,
,
,
, расположенных внутри круга в точках
,
;
,
,
.
Значения параметров
можно выбрать так, чтобы положения зарядов соответствовали точным решениям задачи о проводящем круге, экранированном соответствующей прямой, а именно:
;
;
;
.
Приведенные выше формулы существенно упрощаются при симметричном расположении круга в экранирующем его прямоугольнике, когда центр круга совпадает с центром прямоугольника, тогда
. Симметрия расположения круга в прямоугольнике позволяет редуцировать энергетическую матрицу, уменьшив ее ранг на две единицы, так как
,
.
Если ввести новые обозначения, то можно записать:
;
.
Для более симметричной фигуры, квадрата получим
;
,
тогда число определяемых параметров можно сократить до двух
;
,
а функционал энергии представить в виде
Элементы редуцированной матрицы будут определяться как
(16)
,
где
;
.
Рассмотрим численный пример для круга с радиусом
, экранированного в квадрате со стороной
так, что центры квадрата и круга совпадают. С помощью формул (16) находим элементы матрицы
, далее, минимизируя функционал энергии (15) по
при условии
,
получаем оценку снизу
для емкости конденсатора, образованного границами круга и квадрата как обкладками. Результаты приведены в таблице 1.
Здесь
- значение емкости экранированного в квадрате круга, полученные в работе [7]. Результат, по утверждению автора [7], получен со всеми точными цифрами, однако вычисленная здесь оценка снизу позволяет усомниться в этом. По-видимому, все же погрешность найденной в [7] оценки не будет превосходить нескольких единиц четвертого после запятой знака.
Таблица 1.
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
0.4205
0.5934
0.7814
1.0080
1.3007
1.7059
2.3194
3.3909
5.9170
0.422
0.596
0.780
1.008
1.302
1.704
2.318
3.390
5.920
В заключение отметим, что использование комплексной формы записи электростатических соотношений позволило компактно описать развитую здесь вариационную схему аппроксимации электрических полей проводников полями экранированных точечных зарядов. С помощью этой схемы вычисления практически можно проводить с наперед заданной точностью, выбирая соответствующим образом число аппроксимирующих зарядов. Отметим также, что в настоящей работе впервые было получено выражение для комплексной функции Грина прямоугольника.
Список литературы
- Казанцев В.П., Золотов О.А., Долгополова М.В. // УФН – 2006 – Т.176 - №5 – С. 537 – 542.
- Казанцев В.П., Золотов О.А., Долгополова М.В. // Вестник КрасГУ – 2005 - №4 – С15.
- Казанцев В.П. // ДАН -2001 – Т.380 - №6 – С.749 – 753.
- Казанцев В.П. // Известие вузов. Физика – 2001 - №7 – С.78 – 83.
- Казанцев В.П., Золотов О.А., Долгополова М.В. // Вестник КрасГУ – 2006 - №7 – С.12.
- Полиа Г. Изопериметрические неравенства в математической физике/ Г. Полиа, Г. Сеге. – М.: ГИФМЛ, 1962.
- Пергаменцева Э.Д. // Журн. Техн. Физ. – 1978 – Т.48 - №6 – С.1153 – 1155.
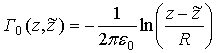
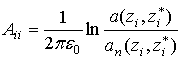 ,
,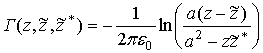 .
(10)
.
(10)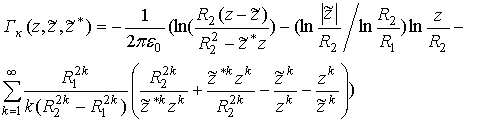 . (11)
. (11)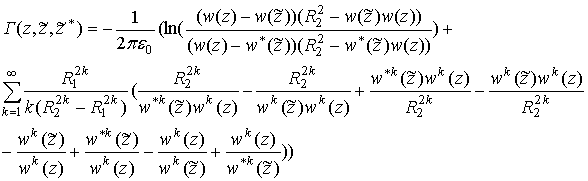 (13)
(13)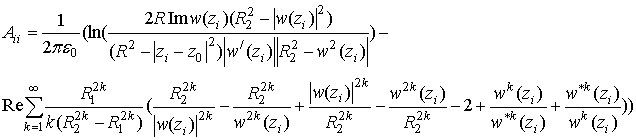
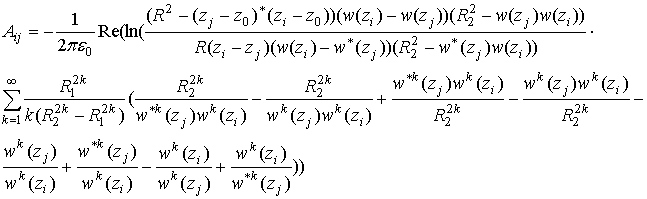
 ,
,