МЕЗОСКОПИЧЕСКИЕ ФЛУКТУАЦИИ ПРОВОДИМОСТИ КРЕМНИЕВЫХ ПОЛЕВЫХ ТРАНЗИСТОРОВ С ВЫСОКОЙ КОНЦЕНТРАЦИЕЙ ВСТРОЕННЫХ ЗАРЯДОВ
А. С. Бугаев, А. С. Веденеев, А. М. Козлов, П. А. Рузанов
Институт радиотехники и электроники РАН
Получена 3 июня 2008 г.
Проводимость G инверсионного n-канала транзисторных Si-МНОП (метал-нитрид-окисел-полупроводник) структур с высокой концентрацией встроенных зарядов (≥1013 см-2) вблизи интерфейса Si-SiO2 обнаруживает в режиме эффекта поля мезоскопические флуктуации зависимости G от потенциала затвора Vg при температуре 4.2. К. Флуктуации G связываются с перестройкой конечной перколяционной сетки, образуемой точечными квантовыми контактами, возникающими в перевальных областях флуктуационного потенциала (ФП), и нелинейным вкладом точечных квантовых контактов в зависимость G от Vg. Показано, что уменьшение Vg в диапазоне G ≤ 2e2/h приводит к увеличению числа точечных квантовых контактов на одиночном пути протекания от 1 до ≤ L/Rs, где L – длина затвора, Rs – радиус экранирования ФП. Мезоскопические особенности зависимости G от Vg и подходы к их анализу подтверждаются результатами численного моделирования.
Практические структуры современной микро- и наноэлектроники, реализуемые на базе МДП (металл-диэлектрик-полупроводник) систем, в настоящее время являются типовыми представителями класса разупорядоченных электронных систем вследствие повышенного содержания встроенных (примесных) зарядов, индуцирующих флуктуационный потенциал (ФП) границы раздела полупроводник-диэлектрик. Современная практика увеличения интеграции СБИС, а также повышения быстродействия исполнительных элементов, полевых транзисторов, достигается за чет увеличения концентрации примесей в подзатворной области транзисторов и/или снижения рабочих напряжений. Например, в типовых транзисторах типа HEMT [1] концентрация встроенных зарядов Nt ≥ 1012 см-2, а характерная амплитуда ФП
Δ ≥ 20 мэВ [2] превышает kT при азотных и почти комнатных температурах (e – элементарный заряд,
– средняя диэлектрическая проницаемость границы раздела полупроводник-диэлектрик, k – постоянная Больцмана).
В наших недавних работах [3,4] показано, что полевые транзисторы с повышенным содержанием встроенных зарядов проявляют мезоскопические свойства проводимости G при пониженных рабочих напряжениях. Например, в транзисторах с длиной затвора 5 - 10 мкм и инверсионным n- и p- каналом зависимость G от потенциала затвора Vg обнаруживает в режиме эффекта поля область квази-плато при G ≈ 2e2/h в области температур от 77 и вплоть до комнатных. Также показано, что в этих структурах радиус корреляции перколяционного кластера превышает длину затвора в экспериментальных условиях, что и обосновывает наблюдение мезоскопических явлений в проводимости структур микронных размеров. Квантовые особенности G связываются с тем, что при повышенной концентрации встроенных зарядов, источников ФП, проводимость приобретает перколяционный характер [6]. В ситуации, когда радиус корреляции перколяционного кластера превышает длину затвора, электронный перенос преимущественно осуществляется по одиночному, наиболее низкоомному пути протекания и лимитирован одиночной наиболее резистивной областью этого пути - критическим элементом конечной перколяционной сетки [6], т.е. – одиночной седловой областью ФП [2]. Отметим, что при Nt ≥ 1012 см-2 перевальные области ФП проявляют свойства точечных квантовых контактов [7,8] по критерию
≥ kT [2,8,9] (m- эффективная масса электрона). По этой причине проводимость инверсионного канала полевых транзисторов с микронной длиной затвора проявляет квантовые 2e2/h свойства при высоких температурах, вплоть до комнатных (см.[3-5]).
Между тем, учитывая вероятностный характер электронного переноса в рассматриваемой мезоскопической ситуации, остается неясным вопрос о структуре конечного перколяционного кластера, образуемого точечными квантовыми контактами и экспериментальном проявлении свойств этих контактов в структуре кластера. Изучению этого вопроса и посвящена настоящая работа.
В режиме эффекта поля исследованы модельные Si-МНОП (метал-нитрид-окисел-полупроводник) транзисторы с инверсионным n- каналом. Длина L и ширина затвора составляли 5 и 50 мкм соответственно, толщины затворного изолятора: Si3N4 – 350 нм, SiO2 – 25 нм. Интерес к структурам связан с тем, что область границы раздела SiO2- Si3N4 содержит электронные ловушки, заряд которых задается и/или изменяется путем полевой инжекции электронов из кремния при комнатных температурах и контролируется по смещению порога зависимости G от Vg [10,11]. При температуре Т = 4.2 К и малом (≤ 0.1 мВ) продольном напряжении по модуляционной методике исследовался кондактанс инверсионного канала структур G как синхронное отношение силы продольного тока к продольному напряжению.
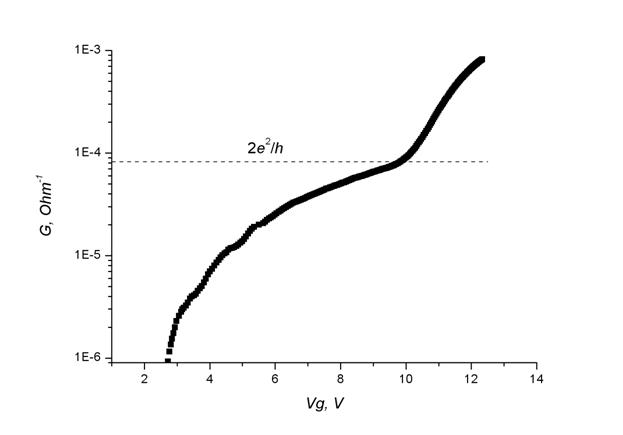
Рис.1. Зависимость проводимости Si-МНОП транзистора от потенциала затвора для Nt ≈ 1.3∙1013 см-2 (пунктирная линия – 2e2/h).
На рис.1 приведена типовая зависимость G от Vg для концентрации встроенных зарядов Nt ≈ 1.3∙1013 см-2. Зависимость иллюстрирует экспоненциальное нарастание G с Vg вблизи порога проводимости [11], область квази-плато в диапазоне G ≈ e2/h [7,8] и последующий переход к квази-2D проводимости при повышенных Vg > eNt/C [2], здесь С –удельная емкость подзатворного изолятора.
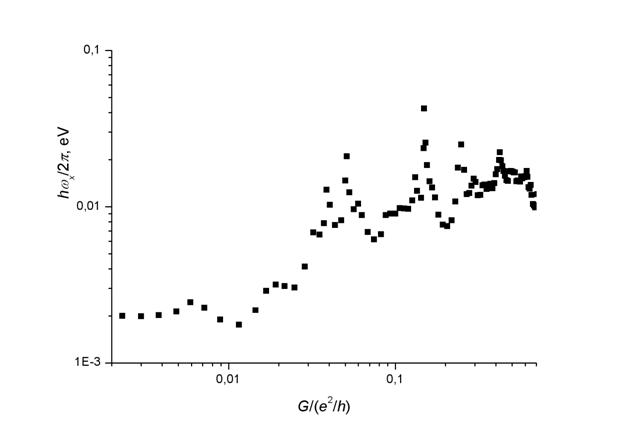
Рис.2. Параметр ħωx в зависимости от нормированной проводимости.
Рис.2 иллюстрирует поведение параметра
, определенного по [3],
характеризующего кривизну одиночной перевальной (седловой) области ФП в направлении движения электронов [7] (здесь
– плотность состояний в 2-D электронном канале,
= G/(2e/h - G). Значение
~ 10 мэВ в области плато (G ≈ e2/h) хорошо совпадает с результатами расчета по методике [4], а спад ħωx с уменьшением Vg в диапазоне G ≤ e2/h связывался в [4] с отличием распределения потенциала в седловой области ФП от параболического закона и уменьшением плотности электронных состояний в "хвосте" флуктуационных состояний [2].
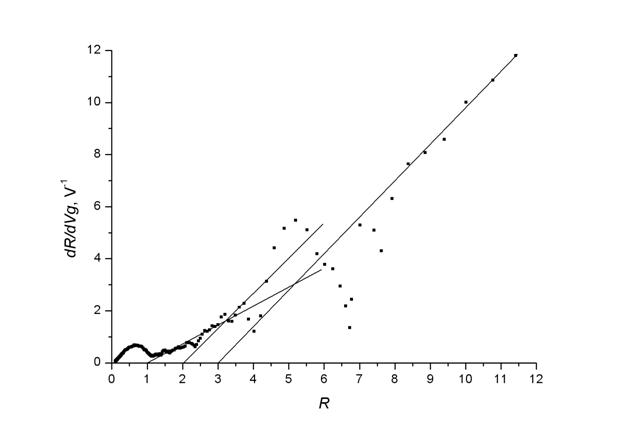
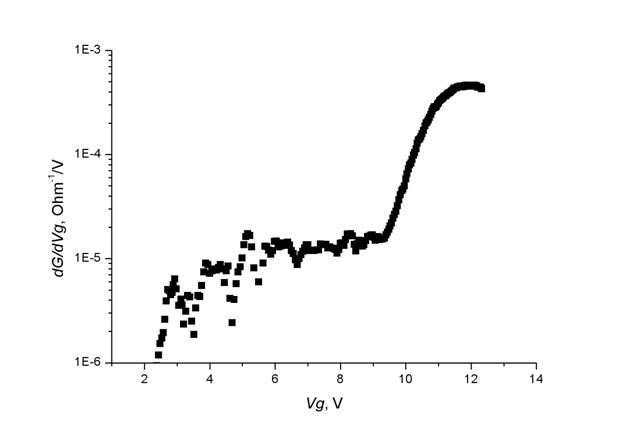
Рис.3. Производная dG/dVg в зависимости от Vg.
Покажем, что спад анализируемого параметра
при G ≤ e2/h может иметь иную природу и, в частности, быть связанным с перестройкой одиночного пути протекания под действием эффекта поля. Обращаясь к экспериментальной зависимости производной dG/dVg от Vg (рис.3) отметим ее регулярные флуктуации в области G < e2/h. Будем считать, что эти флуктуации имеют мезоскописескую природу и обусловлены перестройкой одиночного пути протекания под действием эффекта поля.
Действительно, одиночный путь протекания представляет собой последовательность флуктуационных потенциальных ям, заполненных электронами, связанных перевальными областями ФП [2,6] как точечными квантовыми контактами [8]. Эти квантовые контакты разбросаны по энергии в меру характерной амплитуды ФП Δ ≈ (e2/κ)(πNt)1/2 [2], а их число N ~ L/Rs, где Rs – радиус экранирования ФП [2]. В нашем случае Δ ≈ 100 мэВ, а N ~ 50. Следуя [6] очевидно, что "глубокие" контакты, расположенные по энергии существенно ниже уровня протекания, не вносят заметной вклад в G в силу малого локального сопротивление, а действующими оказываются лишь контакты, попадающие в энергетическую полосу ≈ ħωx/2π ниже уровня протекания (см.[6,8]). Соответственно,
а суммарное сопротивление структуры R, нормированное на величину h/2e2, суть
где нормированное сопротивление i-ого контакта
- энергия Ферми, Vi – энергетический уровень i-ой седловой точки ФП,
– параметр, характеризующий кривизну перевальной области ФП в направлении, поперечном движению электронов [7].
Учитывая экспоненциальный характер зависимости R от
, а также то обстоятельство, что
в анализируемых условиях практически линейно изменяется с Vg, получаем
то есть dR/dVg является линейной функцией R, а результат ее экстраполяции к оси аргумента определяет величину N.
Рис.4. Начальный участок зависимости dR/dVg от R.
Начальный участок экспериментальной зависимости dR/dVg от R приведен на рис. 4. В соответствии с (4) функция имеет выраженные линейные участки, однако результат экстраполяции этих участков к оси аргумента отчетливо демонстрирует изменение числа действующих квантовых контактов N с Vg: если N = 1 при G ≈ e2/h то с уменьшением Vg число N возрастает до » 8.
Мы связываем обнаруженное изменение числа N с нелинейностью системы точечных квантовых контактов по отношению к эффекту поля. Действительно, обращаясь к рис.1, отметим две области, соответствующие различному характеру электронного переноса. В первой из них, при G £ e2/h, преобладает туннелирование электронов через точечный кантовый контакт, тогда как во второй области основной вклад в проводимость вносят свободные электроны, о чем, например, свидетельствует возникновение эффекта Холла при G ³ e2/h [3]. Такое пороговое поведение проводимости естественно связывать с тем, что квантовый контакт [7] проявляет свое сопротивление (4) лишь при энергиях, близких к положению седловой точки Vi, тогда как при
электроны оказываются в области квази-непрерывного спектра [2], а локальное сопротивление контакта Ri практически обращается в нуль. Энергия Ферми, изменяющаяся при эффекте, поочередно пересекает пороги перехода перевальных областей ФП от одного режима проводимости к другому, что и приводит к изменению числа действующих квантовых контактов на пути протекания.
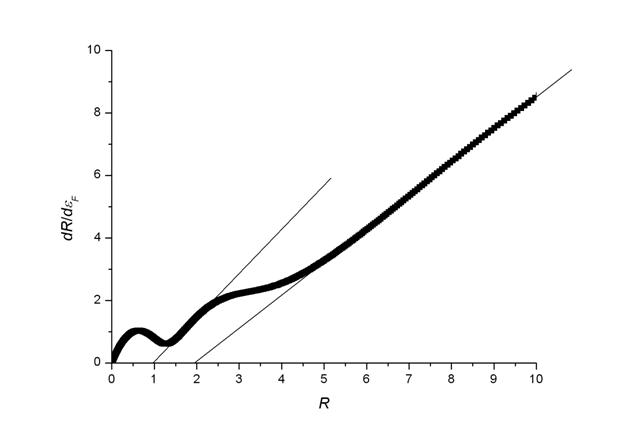
Рис.5. Начальный участок расчетной зависимости
от R.
Вывод о нелинейном поведении системы точечных квантовых контактов подтверждают результаты численного моделирования. На рис.5 приведена расчетная зависимость
для цепочки из четырех точечных квантовых контактов, сопротивление которых, в отличие от (4) задавалось в виде
, (6)
где
и
– параметры. Из сравнения данных рис.4 и 5 видно согласие характера поведения расчетной и экспериментальной функций, что и подтверждает вывод о природе обнаруженных мезоскопических флуктуаций проводимости. Из рис.4 и 5 также следует, что определение
по (1) без учета отличия числа N от единицы приводит к занижению этого параметра в диапазоне G < e2/h.
Таким образом, обнаруженные мезоскопические флуктуации проводимости инверсионного канала полевых транзисторов с высокой концентрацией встроенных зарядов связан с нелинейным поведением системы точечных квантовых контактов при эффекте поля. С этим механизмом также частично связан наблюдаемый спад параметра ħωx с уменьшением потенциала затвора Vg.
Работа выполнена при поддержке РФФИ (06-02-17529-а) и РНП (2.1.4639).
Литература
1. М. Шур. Современные приборы на основе арсенида галлия (М., Мир, 1991). [Пер. с англ.: M.Shur. GaAs Devices and Circuits (Plenum Press, N.Y.-London, 1987)].
2. В.А.Гергель, Р.А.Сурис. ЖЭТФ, 84, 719 (1987).
3. Б.А.Аронзон, Д.А.Бакаушин, А.С.Веденеев и др. ФТП, 35, 448 (2001).
4. А.Б.Давыдов, Б.А.Аронзон, Д.А.Бакаушин, А.С.Веденеев. ФТП, 36, 1241 (2002).
5. А.С.Веденеев, М.А.Феклисов. ФТП, 40, 1069 (2006).
6. Б.И.Шкловский, А.Л.Эфрос. Электронные свойства легированных полупроводников (М., Наука, 1979).
7. M.Buttiker. Phys.Rev.B, 41, 906 (1990).
8. Y.Meir. Phys.Rev.Lett., 83, 3506 (1999).
9. Й Имри. Введение в мезоскопическую физику (М., Физматлит, 2002). [Пер. с англ.: Y.Imry. Introduction to Mesoscopic Physics (Oxford, University Press, 2002)].
10. Т.Андо, А.Фаулер, Ф.Стерн. Электронные свойства двумерных систем (М., Мир, 1985). [Пер. с англ.: T.Ando, A.Fauler, F.Stern. Rev.Mod.Phys., 54, 437 (1982)].
11. С.Зи. Физика полупроводниковых приборов (М., Мир, 1984). [Пер. с англ.: S.M.Sze. Physics of Semiconductor Devices (J.Willey & Sons, N.Y., 1981)].
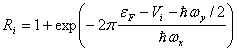 , (4)
, (4)