УДК 539.3; 537.63
МАКСВЕЛЛ-ВАГНЕРОВСКАЯ РЕЛАКСАЦИЯ В ПЬЕЗОКОМПОЗИТЕ PVF/ФЕРРИТ С ЭЛЛИПСОИДАЛЬНЫМИ ВКЛЮЧЕНИЯМИ В ПЕРЕМЕННОМ ЭЛЕКТРИЧЕСКОМ ПОЛЕ
А. А. Паньков
Пермский национальный исследовательский политехнический университет
Получена 2 июня 2013 г., после доработки - 30 июня 2013 г.
Аннотация. Проведен численный расчет и анализ влияния максвелл-вагнеровской релаксации на действительные и мнимые части эффективных коэффициентов электромагнитной связи полидисперсного пьезокомпозита PVF/феррит с эллипсоидальными ферритовыми включениями, слоями и волокнами величины наполнения, формы включений в переменном электрическом поле. Выявлен эффект значительного увеличения продольного коэффициента электромагнитной связи для композита с ориентированными игольчатыми ферритовыми включениями в сравнении с аналогичным коэффициентом для однонаправленного волокнистого или слоистого композитов.
Ключевые слова: пьезокомпозит, электромагнитоупругость, максвелл-вагнеровская релаксация, полидисперсная структура.
Abstract. Numerical calculation and the analysis of influence of makswell-wagner relaxation on the real and imaginary parts of effective electromagnetic factor of polydisperse piezocomposites: PVF/ferrite with ellipsoidal ferrite inclusions, layers and fibers of size of filling, a form of inclusions in variation electric field is carried out. The effect of significant increase in longitudinal effective electromagnetic factor for a composite with unidirectional needle ferrite inclusions in comparison with similar coefficient for unidirectional fibrous or layered composites is revealed.
Keywords: piezocomposite, electro-magnetic elasticity, maxwell‑wagner relaxation, polydisperse structure.
Введение
Магнитоэлектрические
материалы являются одними из наиболее перспективных функциональных материалов
современной электроники [1‑7]. В них сочетаются диэлектрические,
пьезоэлектрические, упругие, пьезомагнитные и магнитные свойства, которыми
можно эффективно управлять с помощью внешних воздействий. Магнитоэлектрические
константы гомогенных магнитоэлектриков очень малы, что обуславливает создание
гетерогенных композиционных магнитоэлектриков, магнитоэлектрические константы
которых могут на несколько порядков превосходить соответствующие константы
гомогенных материалов [5]. В магнитоэлектрических феррит-пьезоэлектрических
композитах магнитоэлектрический эффект отсутствует как в пьезоэлектрической,
так и в ферритовой фазах; его возникновение в композитах связано с
пьезоэлектромагнитным взаимодействием пьезоэлектрической и ферритовой подсистем
через упругие деформационные поля. Учет проводимостей 
фаз
и частоты 
приложенного
электрического поля через комплексную форму записи [5,6]
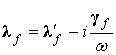(1)
тензоров
диэлектрических проницаемостей 
фаз с действительными
частями 
приводит к комплексным значениям искомых
тензоров эффективных пьезоэлектромагнитных свойств композита, например, тензор
эффективных коэффициентов электромагнитной связи
(2)
будет иметь
как действительную 
, так и мнимую 
части и, как следствие, к возникновению
на макроуровне композита дисперсии и энергетических потерь в переменных
электрических полях, известных под названием «максвелл-вагнеровская
релаксация»; 
‑ число различных фаз в композите.
В [6] исследована максвелл-вагнеровская релаксация феррит-пьезоэлектрических
слоистых композитов, приведен анализ концентрационных и частотных зависимостей
действительных и мнимых частей эффективных электромагнитных констант.
Цель работы ‑ исследование влияния частоты электрического поля, формы и объемной доли ориентированных эллипсоидальных ферритовых включений в полимерном пьезоэлектрике PVF [8] с максвелл-вагнеровской релаксацией (1) на эффективные коэффициенты электромагнитной связи (2) композита на основе полученного ранее [9] нового решения связанной краевой задачи электромагнитоупругости в обобщенном сингулярном приближении статистической механики композитов с использованием новых решений для сингулярных составляющих вторых производных функций Грина для однородной трансверсально-изотропной пьезоэлектромагнитной среды с эллипсоидальным зерном неоднородности.
1. Определяющие соотношения на микро и макро уровнях композита
Для каждой фазы 
в представительной области
двухфазного композита 
запишем определяющие
соотношения [1‑5]
,
, (3)
,
связывающие напряжения 
, индукции электрического 
и магнитного 
полей
с деформациями 
, напряженностями электрического
и магнитного 
полей,
однородным внешним нагревом 
через считающиеся
известными для каждой фазы 
тензоры упругих
свойств 
, пьезоэлектрических 
и пьезомагнитных 
свойств,
диэлектрических 
и магнитных 
проницаемостей, температурных
коэффициентов 
, пироэлектрических 
и пиромагнитных 
постоянных.
Искомые тензоры эффективных
пьезоэлектромагнитных свойств: 
, 
, 
, 
, 
и,
дополнительно, новые тензоры 
, 
электромагнитной связи входят в
определяющие соотношения на макроуровне композита
,
, (4)
,
где макроскопические значения
напряжений 
и деформаций 
,
индукций 
, 
и
напряженностей 
, 
; 
‑ оператор осреднения по области .
Ненулевые компоненты рассматриваемых
трансверсально-изотропных тензоров 
, 
, 
, 
, 
, на
микро (3) и на макро (4) уровнях композита можно наглядно представить в
матричной форме записи [1,2,10]; например, матрицы пьезомодулей
,
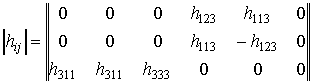
и эффективных коэффициентов электромагнитной связи
,
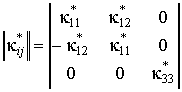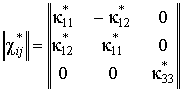(5)
2. Эффективные свойства пьезокомпозита с эллипсоидальными включениями
В [9] получено уточненное решение для тензоров эффективных пьезоэлектромагнитных и термоупругих свойств (4)
, 
, 
, 
, (6)
, 
, 
через поправки 
,…, 
к
соответствующим осредненным по объему значениям 
, …, 
. Тензоры поправок ,…,
(6) получены на основе новых решений [9]
для компонент тензоров сингулярных
составляющих 
вторых производных для функций Грина 
, (7)
,
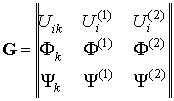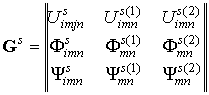(8)
для
однородной анизотропной пьезоэлектромагнитной среды, где 
, 
, 
‑ дельта-функция Дирака, в точке 
действует единичная объемная сила, или
электрический или магнитный источник, 
‑
оператор дифференцирования по координатам вектора 
.
Компоненты матрицы (7), (8) вычисляются по
формулам
, 
, 
;
, 
, 
;
, 
, 
,
где оператор [11]
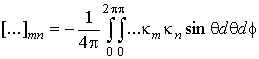
действует на компоненты тензоров
,
,
,
,
,
,
,
,
,
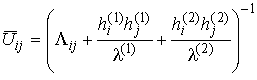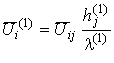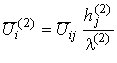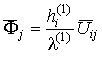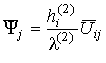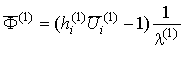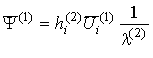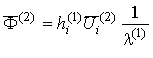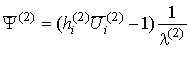где
, 
,
(9)
, 
,
,
,
,
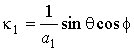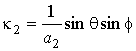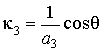и 
‑ полярные углы
в сферической системе координат, поверхность эллипсоидального «зерна
неоднородности» [11] задана равенством
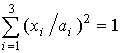(10)
через значения главных полуосей 
, 
–
координаты вектора 
, тензоры 
, 
, 
, 
, 
задают свойства «среды сравнения» [11].
Отметим, что обобщенное сингулярное приближение [9,11]
соответствует предельно полидисперсным структурам [12,13] типа «статистическая
смесь», у которых отсутствует корреляция физико-механических свойств в
произвольных различных точках среды; форма включений учитывается через форму
зерна неоднородности (10), «матричность» или непрерывность какой-либо фазы –
через приравнивание свойств среды сравнения к свойствам этой фазы и в случае,
когда свойство матричности отсутствует, тогда свойства среды сравнения
приравниваются к искомым эффективным свойствам композита ‑ «схема
самосогласования» [11‑13]. Рассматриваемые двухфазные матричные по 2-й
фазе полидисперсные структуры с эллипсоидальными ориентированными включениями
1-й фазы представим совокупностью составных частиц – это эллипсоиды 1-й фазы,
окруженные эллипсоидальными оболочками 2-й фазы. Размеры частиц варьируются в
широких пределах, включая и бесконечно малые, что обуславливает возможность
заполнения ими всей области композита; отношение
главных полуосей внутреннего и наружного эллипсоидов для всех частиц одинаково
и равно 
, где 
‑
относительное объемное содержание 1-й фазы в композите. Такая структура
сохраняет свойство матричности по 2-й фазе при всех возможных степенях
наполнения 
области 1-й
фазой.
3. Численный расчет
Проведем численный расчет и анализ влияния максвелл-вагнеровской релаксации на действительную и мнимую части эффективного продольного коэффициента электромагнитной связи
полидисперсного двухфазного пьезокомпозита PVF/феррит с эллипсоидальными
ферритовыми (1-я фаза) включениями, слоями и волокнами величины наполнения 
, параметра формы включений 
и круговой частоты 
переменного электрического поля, 
(10). Решение для искомого эффективного
коэффициента 
(11) получим из формул обобщенного
сингулярного приближения (6) [9], приняв в (9) равенства
, 
, 
, 
, 
,
т.е. свойства среды сравнения приравниваем к свойствам пьезоэлектрика PVF ‑ 2-я фаза или матрица композита.
Независимые постоянные трансверсально-изотропных магнитоупругих свойств феррита [14]: упругие константы
Па, 
Па
изотропных
упругих свойств, трансверсально-изотропные пезомагнитные свойства с осью
симметрии 
заданы через пьезомодули
Тл, 
Тл, 
Тл
и магнитные проницаемости
=
Тл.м/А,
=
Тл.м/А.
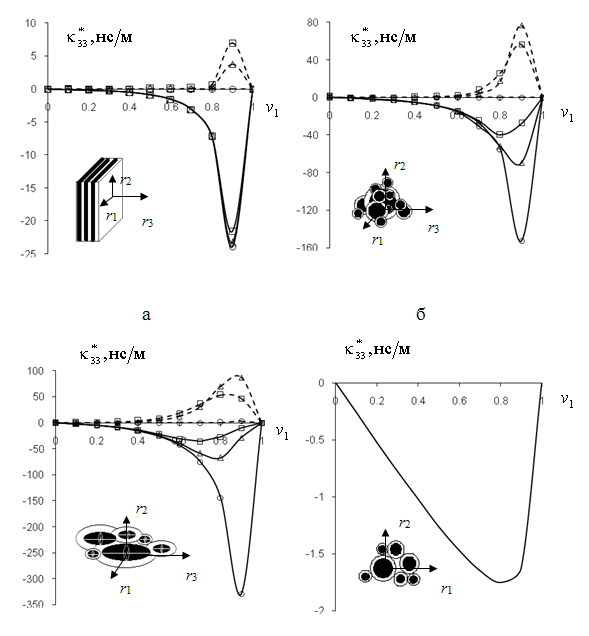
Рисунок. Зависимости действительной
(сплошная линия) и мнимой (штриховая линия) частей коэффициента
магнитоэлектрической связи 
композита PVF/феррит
от объемной доли 
ферритовых слоев (а),
сферических (б), игольчатых (в) включений, волокон (г) при круговой частоте
электрического поля 
(
), 
(
), 
(
)
Трансверсально-изотропные электроупругие свойства
полимерного пьезоэлектрика PVF с
осью симметрии 
приведены в [8,14]: упругие константы
Па, 
Па,
Па, 
Па, 
Па;
действительные части относительных диэлектрических проницаемостей
, 
;
пьезоэлектрические модули
Кл/м2, 
Кл/м2, 
Кл/м2,
диэлектрическая
проницаемость вакуума 
Ф/м.
Дополнительно принимаем, что для феррита тензор
пьезоэлектрических свойств 
,
проводимости 
(Ом×м)-1 [6] и диэлектрические
проницаемости 
[4] никелевой
феррошпинели; для пьезоэлектрика PVF тензор пьезомагнитных свойств 
, проводимости 
(Ом×м)-1 полиэтилена
[15], магнитные проницаемости 
Тл.м/А
вакуума.
На рисунке представлены результаты расчета концентрационных
зависимостей действительной 
и мнимой 
частей коэффициента магнитоэлектрической
связи (11) композита PVF/феррит от объемной
доли ферритовых слоев (
)
(рис., а), сферических (
) (рис., б), игольчатых
(
) (рис., в) включений, волокон (
) (рис., г) при различных значениях
круговой частоты электрического поля.
4. Выводы
Выявлено значительное увеличение продольного коэффициента 
для композита с игольчатыми включениями
ориентированными по оси (рис., в) в сравнении
со значением для однонаправленного волокнистого
композита (рис., г); эффект особенно проявляется при низкочастотном нагружении 
и высокой степени наполнения 
ферритовыми включениями. Для сферических
(рис., б) ферритовых включений этот эффект также имеет место, но выражен
немного менее ярко. Коэффициент для однонаправленного
волокнистого композита (рис., г) не зависит от частоты и
его мнимая часть 
. Подтверждено, что для частных
случаев структур: слоистой (рис., а) и однонаправленной волокнистой (рис., г)
из обобщенного сингулярного приближения [9] следуют точные решения для
эффективного коэффициента электромагнитной связи слоистой
[10] и полидисперсной волокнистой 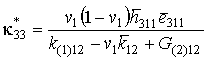[12]
(12)
структур в
случае, когда свойства среды сравнения приравнены к свойствам матрицы (2-й
фазы) композита, где разности: 
, 
, 
,
объемный модуль плоской деформации 
и модуль сдвига 
в плоскости изотропии 
. Дополнительно отметим, что аналитическое
решение для (12) при инверсии фаз в точности совпало
с решением [2] асимптотического метода осреднения для композита
феррит/пьезоэлектрик с идеальной периодической волокнистой структурой.
1. Партон В.З. Электромагнитоупругость пьезоэлектрических и электропроводных тел / В.З. Партон, Б.А. Кудрявцев. М.: Наука, 1988. 472 с.
2. Гетман И.П. О магнитоэлектрическом эффекте в пьезокомпозитах // ДАН СССР. 1991. Т. 317, № 2. С. 341-343.
3. Коган Л.З., Мольков В.А. Магнитоэлектрические свойства волокнистых пьезокомпозитов // Изв. РАН. Механика твердого тела. 1996. № 5. С. 62-68.
4. Турик А.В., Чернобабов А.И., Родинин М.Ю., Толокольников Е.А. Магнитоэлектричество в двумерных статистических смесях // Физика твердого тела. 2009. Т. 51. № 7. С. 1395-1397.
5. Турик А.В., Чернобабов А.И., Родинин М.Ю. Гетерогенные мультиферроики: магнитоэлектричество и пьезоэффект // Физика твердого тела. 2009. Т. 51. № 8. С. 1580-1583.
6. Петров В.М., Бичурин М.И., Srinivasan G. Максвелл-вагнеровская релаксация в магнитоэлектрических композиционных материалах // Письма в ЖТФ. 2004. Т. 30. № 8. С. 81-87.
7. Филиппов Д.А. Теория магнитоэлектрического эффекта в гибридных феррит-пьезоэлектрических композиционных материалах // Письма в ЖТФ. 2004. Т. 30. № 9. С. 6-11.
8. Sessler G.M. Piezoelectricity in polyvinylidenefluoride // J. Acoust. Soc. Amer. 1981. Vol. 70. № 6. P. 1596-1608.
9. Паньков А.А. Коэффициенты электромагнитной связи композита с пьезоактивными фазами // Физическая мезомеханика. 2011. Т. 14. № 2. С. 93-99.
10. Паньков А.А. Влияние искривления слоев на коэффициенты электромагнитной связи пьезокомпозита // Механика композиционных матеpиалов и констpукций. 2012. Т. 18. № 2. С. 155-168.
11. Шеpмеpгоp Т.Д. Теоpия упpугости микpонеодноpодных сpед. М.: Наука, 1977. 400 с.
12. Паньков А.А. Пьезоактивные однонаправленно волокнистые полидисперсные композиты // Механика композитных материалов. 2012. Т. 48. № 6. С. 873-886
13. Кристенсен Р. Введение в механику композитов. М.: Мир, 1982. - 334 с.
14. Хорошун Л.П. Прогнозирование эффективных свойств пьезоактивных композитных материалов / Л.П. Хорошун, Б.П. Маслов, П.В. Лещенко. Киев: Наук. думка, 1989. 208 с.
15. Турик А.В., Радченко Г.С. Гигантский пьезоэлектрический эффект в слоистых композитах сегнетоэлектрик-полимер // Физика твердого тела. 2003. Т. 45. № 9. С. 1676-1679.