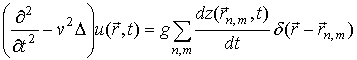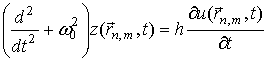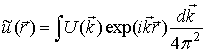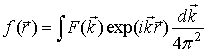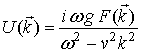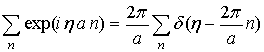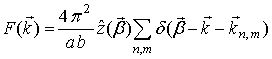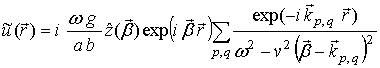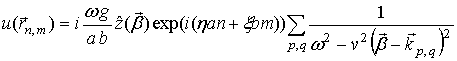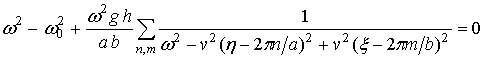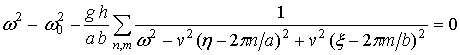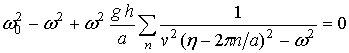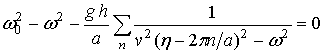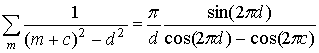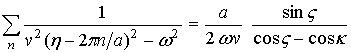УДК 534.212

 

Дисперсионные соотношения для решетки глобально связанных осцилляторов

 

В. Н. Корниенко ¹⁾, А. П. Привезенцев ²⁾, В. А. Черепенин ¹⁾

 

¹⁾ ИРЭ им. В.А.Котельникова РАН

²⁾ Челябинский государственный университет

Получена 12 июня 2013 г.

 

Аннотация.        В работе получены дисперсионные соотношения для двумерной решетки и одномерной цепочки осцилляторов, связанных через общее поле. Рассмотрены случаи, когда связь осуществляется через смещения осцилляторов и их производные по времени. Для одномерного случая получены замкнутые дисперсионные уравнения, содержащие элементарные функции. Проведен анализ поведения дисперсионных характеристик для различных параметров рассматриваемой системы.

Ключевые слова: метаматериалы, осцилляторы, глобальная связь.

Abstract. We obtain the dispersion relations for the two-dimensional lattice and the one-dimensional chain of oscillators coupled by a common field. The two cases (when the communication is done through the displacement of oscillators and their time derivatives) were considered. The closed dispersion equations, which containing elementary functions only, were obtained in one-dimensional case. The analysis of the behavior of dispersion characteristics for the various parameters of the system was done.

Keywords: metamaterials, oscillators, global coupling.

 

Введение

В последнее время значительный научный интерес представляет исследование так называемых метаматериалов – искусственных сред со специфическими электромагнитными свойствами. В частности, известно [1], что возможно создание квазинепрерывной среды, диэлектрическая и магнитная проницаемость которой одновременно принимают отрицательные значения. В этом случае фазовая и групповая скорости распространяющихся волн имеют противоположные знаки. Если в основе такой среды будут лежать пассивные элементы, то ее особые свойства проявятся в очень узкой полосе частот, соответствующей линии поглощения метаматериала. При этом существенное затухание полей, фактически, делает такой материал непригодным для практических применений. Одним из возможных путей преодоления этой трудности является использование активных сред. Так, в [2] описаны попытки их применения для светового диапазона длин волн.

В классической физике в качестве элемента искусственной активной среды можно рассматривать, например, осциллятор с исходно запасенной энергией. Его динамика зависит от состояния поля в месте его расположения, а, значит, будет определяться не только полем внешней волны, но и полями, созданными остальными осцилляторами.

Целью данной работы было исследование дисперсионных свойств двумерной безграничной решетки осцилляторов, взаимодействующих между собой через общее поле.

1. Постановка задачи

Рассмотрим задачу о самосогласованном взаимодействии скалярного волнового поля и двумерной безграничной решетки гармонических осцилляторов. Связь осцилляторов можно считать глобальной, поскольку на каждый элемент решетки действует поле, возбуждаемое всеми осцилляторами.

Осцилляторы расположены в узлах неограниченной двумерной решетки с ячейкой  по осям  и . Положение произвольной точки двумерной области характеризуется вектором , положение узла решетки - вектором .

2. Связь по скорости

Взаимодействие осцилляторов и волнового поля описывают уравнения

                      ,                      (1)

                               ,                               (2)

 

где  –коэффициент связи осциллятора и поля,  - коэффициент связи поля и осциллятора,  – собственная частота осциллятора, . Функция  определяет состояние волнового поля в точке  в момент времени . Величина  соответствует смещению от положения равновесия осциллятора в узле решетки  в момент времени . Значения индексов суммирования в правой части уравнения (1) принимают значения .

Представленный системой (1), (2) тип взаимодействия, когда в правой части уравнений поля и осцилляторов находятся производные по времени от координаты осцилляторов и функции, определяющей состояние поля, будем называть связью по скорости.

Рассмотрим решения системы (1), (2), гармонически зависящие от времени

            , .

В этом случае пространственную структуру волнового поля и ансамбля осцилляторов для связи по скорости определяют уравнения

                                                                            (3)

                                 ,                                 (4)

где.

 

    Используем далее преобразование Фурье по пространственным координатам

                , ,               (5)

 

где , , интегрирование по координатам волнового вектора проводим в бесконечных пределах. Подставляя (5) в (3), получим

                                            .                                            (6)

 

Амплитудный спектр пространственных гармоник функции  имеет следующий вид:

                                  .                                  (7)

 

Будем искать собственные волны решетки в виде

                                     ,                                     (8)

где  – волновой вектор колебаний решетки, .

    Для преобразования суммы по координатам узлов решетки в (7) сумму по координатам решетки в пространстве волновых векторов используем формулу Пуассона

                                .                               (9)

 

Используя (8) и (9) получим

                               ,                              (10)

где

                                          .          

                                

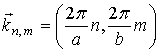Подставляя (10) в (6), можно вычислить интеграл по проекциям волновых векторов в обратном преобразовании Фурье для пространственной структуры волнового поля

                    ,                   (11)

 

При вычислении величины волнового поля в узлах сетки, скалярное произведение  оказывается кратным , т.е.

                .

Таким образом, пространственная зависимость волнового поля, действующего на осциллятор в узле решетки , совпадает с принятой структурой для волны решетки осцилляторов

            .           (12)

 

 

    Подстановка (12) в (4) дает следующее уравнение, определяющее закон дисперсии при связи по скорости:

          .        (13)

 

Закон дисперсии (13) очевидно демонстрирует пространственную дисперсию собственных волн решетки при глобальной связи осцилляторов в ее узлах – зависимость частоты от направления распространения волны. 

3. Связь по координатам

Рассмотрим случай, когда в правых частях системы (1), (2) стоят координата осциллятора  и функция  (связь по смещению):

                        ,                         

                                 ,                                 

 

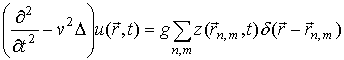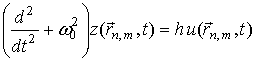Проведя преобразования, аналогичные описанным в п.2, получим следующую связь между частотой и волновым вектором:

           (14)

 

4. Одномерный случай

В случае одномерной структуры с глобальной связью образующих ее элементов выражения (13) и (14) приобретают следующий вид:

при связи по скоростям

                       ,                      (15)

 

при связи по смещениям

                          .                        (16)

 

Используя формулу 3 в п.5.1.25 из [3]

                          ,         

              

можно вычислить суммы в выражениях (15), (16) и получить закон дисперсии, выраженный через элементарные функции. Преобразуем выражение, стоящее под знаком суммы в (15), (16), к виду

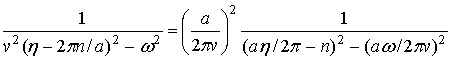             .            (17)

 

Обозначив , , получим для суммы в выражениях (15), (16)

                       ,                      (18)

 

где введены безразмерная частота  и волновой вектор . После подстановки (18) в (15) и переходу к безразмерным переменным, получим для связи по скорости

                ,

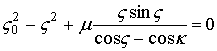где 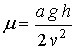 - безразмерный параметр, , или

                              .                            (19)

Волновой вектор принимает значения в интервале . Для цепочки со связью по смещению закон дисперсии имеет вид

                            .                           (20)

Введенные безразмерная частота и волновой вектор соответствуют переходу к безразмерным пространственно-временным переменным, где единицей координаты служит расстояние между осцилляторами – , а единицей времени величина .

    В случае  дисперсионные уравнения (15) и (16) формируют линию  и семейство линий с чередующимся наклоном , для знака «+»  , для знака «-» .Для  эти прямые служат асимптотами линий , которые определяют уравнения (19), (20).

    В области низких частот  и длинных волн  законы дисперсии принимают особенно простой вид. Для связи по скорости

                                  ,                                 (21)

для связи по смещению имеем

                                    .                                   (22)

Заметим, что дисперсионное уравнение (22) для волн решетки аналогично характеристическому уравнению для нормальных частот связанных осцилляторов с собственными частотами  и . Таким образом, зависимость  в этом случае имеет вид известного графика Вина.

На рис.1. представлены дисперсионные характеристики одномерной цепочки при отрицательном значении параметра   и различных значения собственных частот осцилляторов. Аналогичные кривые для случая  приведены на рис.2. Отметим, что при этом в рассматриваемой системе существует положительная обратная связь.

Зависимость ширины зоны непрозрачности от величины коэффициента связи отражена на рис.3.

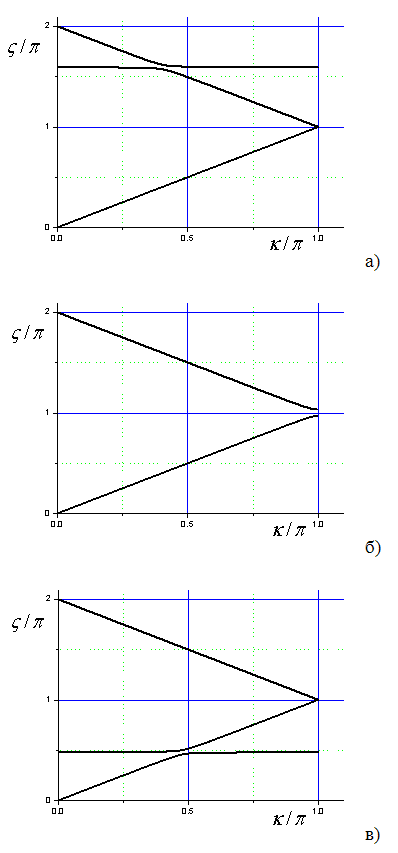
Рис.1. Зависимость частоты от волнового числа при  для  (а),  (б) и  (в).

 

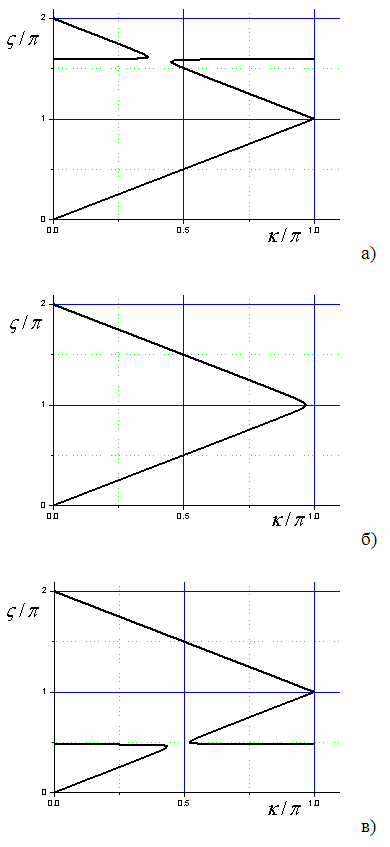
Рис.2. Зависимость частоты от волнового числа при  для  (а),  (б) и  (в).

 

 

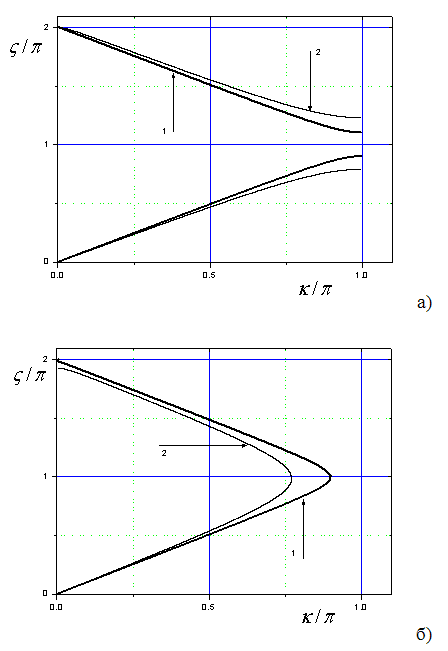
Рис.3. Вид дисперсионных характеристик для отрицательных (а) и положительных (б)
значений коэффициента связи;  (кривые 1) и  (кривые 2). 

5. Комплексные корни дисперсионного уравнения

Запишем дисперсионное уравнение длинноволнового приближения (21) в форме

 

 

 

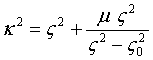
или 

 

 

 

 

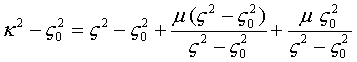
Введем следующие обозначения:

                , .

 

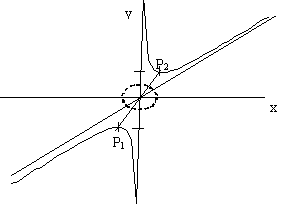
Рис.4. Область комплексных корней (штриховая линия).

 

В результате получим дисперсионное уравнение в виде

        ,        

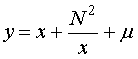где .

Определим далее координаты точек Р₁ и Р₂ (рис.4.), ограничивающих запрещенную зону по координате  из условия, что в этих точках 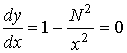. В результате получим

, , , .

Построим далее линию, соединяющую точки Р₁ и Р₂ . Из условия

                ,

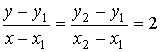получим  уравнение .

Далее, рассмотрим в запрещенной зоне по  комплексное дисперсионное уравнение, введя переменные , . В результате получим

               

Разделяя действительную и мнимую части, получим

               

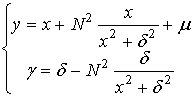
На линии Р₁Р₂ () будем иметь

               

или

                .

 

Пунктирная линия на рис.4. показывает значения мнимой добавки к , связанной с инкрементом по частоте в области частот, соответствующих запрещенной зоне.

Максимальное значение мнимая добавка имеет при точном резонансе  равное .

Для мнимой добавки к  получается нулевое значение. Таким образом, наличие запрещенной зоны связано с неустойчивостью системы по времени.

 Оценим величину инкремента по времени, допуская, что он является малой добавкой к частоте (). Из условия резонанса  при  следует, что .

 

Литература

 

1. В.М.Агранович, Ю.Н.Гартштейн // Усп.физ.наук. 2006. Т.176. №10. С.1051.

 

2. Shumin Xiao, V.P. Drachev, A.V. Kildishev at al // Nature. 05 August 2010. 466. P.735.

 

3. Прудников А. П., Брычков Ю. А., Маричев О. И. Интегралы и ряды. Т. 1. Элементарные функции. — М.: ФИЗМАТЛИТ,2002. - 632 с.