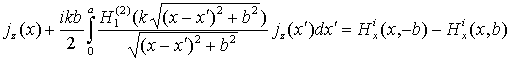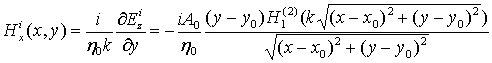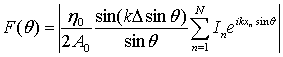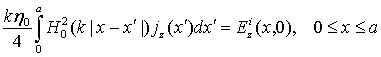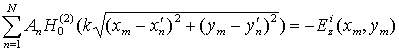УДК 621.396.67
ОБ ОДНОМ ПОДХОДЕ К электродинамическоМУ анализУ тонких идеально проводящих Рассеивателей
С. П. Скобелев
ОАО "Радиофизика", Москва
Московский физико-технический институт
Получена 6 июня 2013 г.
Аннотация. Проводится анализ приближенного интегрального уравнения Фредгольма второго рода, полученного согласно предложенному недавно в литературе подходу к решению задач рассеяния электромагнитных волн слабо искривленными идеально проводящими рассеивателями малой, но ненулевой толщины. Эффективность применения указанного уравнения, основанного на эквивалентном токе, расположенном на незамкнутой поверхности внутри рассеивателя, изучается как аналитически, так и по численным результатам сравнения с методом интегрального уравнения первого рода и методом вспомогательных источников, примененным к решению двумерных задач для ленты. Показано, что аналогично методу физической оптики указанное уравнение не способно учитывать краевые эффекты, проявляющиеся в специфическом поведении плотности тока у края рассеивателя, в возбуждении краевых волн и в возникновении кроссполяризационной составляющей плотности тока. Результаты работы были представлены на 6-й Всероссийской конференции "Радиолокация и радиосвязь".
Ключевые слова: электромагнитное рассеяние, тонкие экраны, численные методы, интегральные уравнения.
Abstract: Analysis of an approximate Fredholm integral equation of the second kind obtained according to an approach proposed recently in the literature for solving the problems of electromagnetic wave scattering by weakly curved perfectly conducting scatterers of small but non-zero thickness is carried out. The effectiveness of application of the indicated equation based on an equivalent current on an unclosed surface arranged inside the scatterer is investigated both analytically and by means of comparison with the method of integral equation of the first kind and with the method of auxiliary sources applied for solving two-dimensional problems for a strip. It is shown that like the method of physical optics, the indicated equation is incapable of accounting for the edge effects resulting in specific behavior of the current at the edges, excitation of the edge waves, and appearing of the crosspolar current component. The results of the work were presented at the 6th All-Russian Conference "Radar and Communications", November 2012, Moscow, Russia.
Key words: electromagnetic scattering, thin screens, numerical methods, integral equations.
1. Введение
В последнее время в литературе появились несколько статей, например [1-4], в которых предложены новые комбинированные методы численного анализа тонких идеально проводящих рассеивателей. В отличие от ранее опубликованной работы [5], где метод физической оптики (ФО) комбинируется с методом интегрального уравнения (ИУ) первого рода, записанного в предположении рассеивателя нулевой толщины, авторы [1-4] предлагают комбинировать метод ФО с методом ИУ второго рода в предположении рассеивателя малой, но ненулевой толщины. Кроме того, в отличие от точного классического ИУ второго рода [6] для тока на всей поверхности рассеивателя, включая освещенную поверхность, затененную поверхность и узкую боковую поверхность (обечайку) авторы [1-3] предлагают два вида новых приближенных ИУ второго рода для тока только на одной поверхности. В первом случае – это незамкнутая поверхность внутри рассеивателя с эквивалентным током на ней, а во втором – уравнение записывается только для тока на освещенной стороне, а ток на теневой стороне учитывается через разность точного тока на освещенной стороне и приближенного тока, определенного по методу ФО. Авторы [1-4] видят преимущество своего подхода в том, что, в отличие от ИУ первого рода, ИУ второго рода дает разреженные матрицы при алгебраизации последнего [7]. Кроме того, в отличие от [5], где области ФО и ИУ не перекрываются, авторы [1-4] предлагают распространять область ФО на всю освещенную поверхность рассеивателя, перекрывая область ИУ у края рассеивателя, и, считая, что решение для тока, полученное методом ФО, уже близко к точному решению, предлагают использовать увеличенный сегмент разбиения области ИУ по сравнению с обычно принятыми размерами, уменьшая тем самым порядок системы алгебраических уравнений.
Работы по повышению эффективности алгоритмов численного анализа больших рассеивателей всегда представляют интерес, однако статьи [1-4], а также и предыдущие статьи [7, 8], посвященные предложенным методам, вызывают ряд вопросов, требующих прояснения, дополнительного анализа и обсуждения. Так, например, указанное выше предположение, что ток, рассчитанный по методу ФО, близок к точному току у края тонкого рассеивателя, противоречит существующим представлениям, основанным на хорошо известных результатах, показывающих, что точный ток у края экрана может существенно отличаться от ФО-тока. Например, составляющая плотности тока, параллельная краю, может возрастать до бесконечности согласно условию Мейкснера [9] в случае острой кромки или до конечной, но большой величины, в случае сглаженной кромки [10]. Результаты сравнения эффективности применения предложенных ИУ второго рода и ИУ первого рода, приведенные в [4] и [7], представляются неполными, так как авторы работают с матрицей системы линейных алгебраических уравнений (СЛАУ), соответствующей ИУ первого рода, записанной для всей поверхности рассеивателя, а не для существенно меньшей ее части, соответствующей области ИУ, как это сделано в [5]. Результаты сравнения с экспериментом, приведенные в [4], также не позволяют судить об эффективности предложенных методов, так как не указано с каким из двух методов проводится сравнение и для сравнения не приведены численные результаты, полученные другими методами, например, методом ФО. Наконец, исследования эффективности самих предложенных ИУ второго рода, проведенные в [3] и [8], также представляются неполными, так как не рассматривалась погрешность выполнения граничных условий и ее сходимость, а также рассматривались не все случаи возбуждения рассеивателя, представляющие интерес.
По причинам, указанным выше, представляет интерес проведение дополнительных аналитических и численных сравнительных исследований ИУ второго рода, предложенных и рассмотренных в [1-4, 7, 8] с целью получения более полной информации об их эффективности для анализа тонких рассеивателей. Дополнительное рассмотрение ИУ, основанного на априорном учете ФО-решения [1, 7], было проведено в [11], где показано, что этот подход для плоских рассеивателей не дает ничего кроме ФО-решения, и поэтому является неэффективным. Ниже проводятся дополнительные исследования подхода, основанного на эквивалентном токе, расположенном на незамкнутой поверхности внутри рассеивателя.
2. Общие соображения
Рассмотрим слабо искривленный идеально проводящий
рассеиватель малой толщины ![]() , возбуждаемый заданным
электромагнитным полем с напряженностями
, возбуждаемый заданным
электромагнитным полем с напряженностями ![]() и
и ![]() . Сечение этого рассеивателя показано на
рис. 1. Внутри рассеивателя выбирается незамкнутая вспомогательная поверхность
. Сечение этого рассеивателя показано на
рис. 1. Внутри рассеивателя выбирается незамкнутая вспомогательная поверхность ![]() , равноудаленная от верхней
, равноудаленная от верхней ![]() и нижней
и нижней ![]() поверхностей.
Предполагается, что на вспомогательной поверхности расположен эквивалентный
электрический ток плостности
поверхностей.
Предполагается, что на вспомогательной поверхности расположен эквивалентный
электрический ток плостности ![]() , создающий рассеянное
поле.
, создающий рассеянное
поле.
Вывод ИУ для введенного эквивалентного тока имеется в [3],
однако приведенные там формулы содержат ошибки. Так ИУ (1) в [3] вместо суммы
токов ![]() , которые находятся на различных сторонах рассеивателя
, которые находятся на различных сторонах рассеивателя ![]() и
и ![]() и не могут характеризоваться одним и
тем же вектором точки наблюдения, должен стоять какой-либо один из токов. Еще
одна ошибка допущена при записи ядра уравнения (13) в [3]: ядро должно быть
представлено не одним членом, а в виде двух слагаемых, как это имеет место в
скалярных уравнениях (10) и (12), из которых (13) составлено. Кроме того, ядра
скалярных уравнений (10) и (12), выведенных в [3], содержат особенности. Этот
факт противоречит предположению о том, что эквивалентный ток расположен на
промежуточной поверхности S,
не соприкасающейся с поверхностями
и не могут характеризоваться одним и
тем же вектором точки наблюдения, должен стоять какой-либо один из токов. Еще
одна ошибка допущена при записи ядра уравнения (13) в [3]: ядро должно быть
представлено не одним членом, а в виде двух слагаемых, как это имеет место в
скалярных уравнениях (10) и (12), из которых (13) составлено. Кроме того, ядра
скалярных уравнений (10) и (12), выведенных в [3], содержат особенности. Этот
факт противоречит предположению о том, что эквивалентный ток расположен на
промежуточной поверхности S,
не соприкасающейся с поверхностями ![]() и
и ![]() , на которых удовлетворяется выполнение
граничного условия.
, на которых удовлетворяется выполнение
граничного условия.
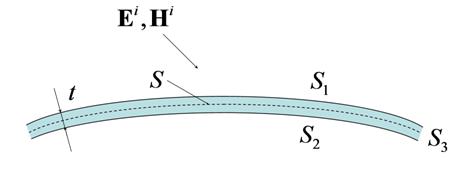
Рис. 1. Сечение тонкого рассеивателя, возбуждаемого сторонним полем.
В связи с наличием указанного противоречия и ошибок в оригинальной работе [3] представляется уместным привести вывод ИУ здесь. Напряженность рассеянного магнитного поля, создаваемого эквивалентным током, определяется через векторный потенциал хорошо известной формулой
![]() ,
(1)
,
(1)
где ![]() – функция Грина,
– функция Грина, ![]() – расстояние между
точками наблюдения и интегрирования,
– расстояние между
точками наблюдения и интегрирования, ![]() – волновое число и
– волновое число и ![]() – длина волны. Пусть
– длина волны. Пусть ![]() и
и ![]() –
радиус-векторы точек наблюдения на поверхностях
–
радиус-векторы точек наблюдения на поверхностях ![]() и
и ![]() соответственно. Плотности токов,
наведенных на указанных поверхностях рассеивателя определяются формулами
соответственно. Плотности токов,
наведенных на указанных поверхностях рассеивателя определяются формулами
![]() ,
(2)
,
(2)
![]() , (3)
, (3)
где ![]() и
и ![]() –
единичные векторы внешней нормали в указанных точках на указанных поверхностях.
В работах [2-4] ток на узкой боковой поверхности рассеивателя
–
единичные векторы внешней нормали в указанных точках на указанных поверхностях.
В работах [2-4] ток на узкой боковой поверхности рассеивателя ![]() не учитывается, и предполагается, что
эквивалентный ток на вспомогательной поверхности равен сумме токов (2) и (3).
Поэтому полагая
не учитывается, и предполагается, что
эквивалентный ток на вспомогательной поверхности равен сумме токов (2) и (3).
Поэтому полагая ![]() и
и ![]() ,
подставляя (1) в (2) и (3), суммируя (2) и (3), а также перенося интегральные
слагаемые в левую часть, получим ИУ второго рода
,
подставляя (1) в (2) и (3), суммируя (2) и (3), а также перенося интегральные
слагаемые в левую часть, получим ИУ второго рода
где ![]() . Заметим, что под интегралом в
(4) стоит разность двух значений функции Грина для точек наблюдения, лежащих
напротив друг друга на разных поверхностях, а соответствующее ИУ (13) в [3]
содержит только одно значение функции Грина, что является ошибкой, упомянутой выше.
Кроме того, в отличие от [3], ядро в (4) не содержит никаких особенностей, как это
и должно быть согласно исходному предположению.
. Заметим, что под интегралом в
(4) стоит разность двух значений функции Грина для точек наблюдения, лежащих
напротив друг друга на разных поверхностях, а соответствующее ИУ (13) в [3]
содержит только одно значение функции Грина, что является ошибкой, упомянутой выше.
Кроме того, в отличие от [3], ядро в (4) не содержит никаких особенностей, как это
и должно быть согласно исходному предположению.
Рассмотрим уравнение (4) применительно к случаю плоского
рассеивателя. Если такой рассеиватель облучается плоской волной, распространяющейся
в плоскости рассеивателя и так, что вектор ![]() ориентирован
параллельно указанной плоскости, то вектор
ориентирован
параллельно указанной плоскости, то вектор ![]() будет
соответственно ориентирован перпендикулярно плоскости рассеивателя. Это
означает, что правая часть (4) обращается в нуль, что дает нулевое решение для
эквивалентного тока и соответственно нулевое рассеянное поле. Но такое решение
задачи было бы ошибочным, так как в действительности ток на поверхности
рассеивателя в рассматриваемом случае не равен нулю, и он создает ненулевое
рассеянное поле, компенсирующее касательное электрическое поле падающей волны
на поверхности.
будет
соответственно ориентирован перпендикулярно плоскости рассеивателя. Это
означает, что правая часть (4) обращается в нуль, что дает нулевое решение для
эквивалентного тока и соответственно нулевое рассеянное поле. Но такое решение
задачи было бы ошибочным, так как в действительности ток на поверхности
рассеивателя в рассматриваемом случае не равен нулю, и он создает ненулевое
рассеянное поле, компенсирующее касательное электрическое поле падающей волны
на поверхности.
Еще одна особенность (4) состоит в том, что если плоский
рассеиватель расположить в плоскости ![]() прямоугольной декартовой
системы координат
прямоугольной декартовой
системы координат ![]() , то уравнение (4) распадется на
два независимых уравнения для составляющих плотности тока
, то уравнение (4) распадется на
два независимых уравнения для составляющих плотности тока ![]() и
и ![]() , что
как раз и использовалось в [3]. Такая особенность означает, что если, например,
прямоугольная пластина с краями, параллельными осям x и y, облучается плоской волной, падающей
по нормали к поверхности и поляризованной, например, вдоль оси y, то правая часть уравнения,
содержащего
, что
как раз и использовалось в [3]. Такая особенность означает, что если, например,
прямоугольная пластина с краями, параллельными осям x и y, облучается плоской волной, падающей
по нормали к поверхности и поляризованной, например, вдоль оси y, то правая часть уравнения,
содержащего ![]() , не будет равна нулю, что даст ненулевое
решение для этой составляющей плотности тока, а правая часть уравнения,
содержащего
, не будет равна нулю, что даст ненулевое
решение для этой составляющей плотности тока, а правая часть уравнения,
содержащего ![]() , будет равна нулю, что даст ноль для этой
кроссполяризационной составляющей тока. Такая же ситуация имеет место, если рассматриваемая
задача решается методом ФО, который не учитывает кроссполяризацию. Однако
хорошо известно, например, из [12, 13], что кроссполяризационная
составляющая тока
, будет равна нулю, что даст ноль для этой
кроссполяризационной составляющей тока. Такая же ситуация имеет место, если рассматриваемая
задача решается методом ФО, который не учитывает кроссполяризацию. Однако
хорошо известно, например, из [12, 13], что кроссполяризационная
составляющая тока ![]() также не равна нулю в
рассматриваемом случае.
также не равна нулю в
рассматриваемом случае.
Заметим, что рассеянное поле в первом случае, рассмотренном выше, является полем краевой волны, а кроссполяризационная составляющая тока во втором случае возникает из-за наличия краев пластины. Таким образом, рассмотренные случаи демонстрируют проявление краевых эффектов, которые никак не выявляются уравнением (4). Частный случай этого уравнения для двумерной задачи рассеяния будет рассмотрен ниже в разделе 3.
Заметим также, что указанные краевые эффекты не смогут быть выявлены и при использовании точного ИУ второго рода [6], из которого удалена боковая поверхность (обечайка) рассеивателя и ток на ней, так оно приобретает те же самые недостатки, что и (4). Поэтому такое "квази-строгое" уравнение, использованное в [3] в качестве эталона, не позволяет судить о точности и достоверности результатов, полученных в [3] и представленных для сравнения.
3. Сравнение методов и результатов
Для проведения дополнительных исследований возможностей ИУ
(4) рассмотрим двумерную задачу рассеяния цилиндрической волны на плоской
идеально проводящей ленте шириной ![]() и толщиной
и толщиной ![]() , расположенной в прямоугольной декартовой
системе координат
, расположенной в прямоугольной декартовой
системе координат ![]() как показано на рис. 2.
как показано на рис. 2.

Рис. 2. Плоская лента ненулевой толщины, возбуждаемая источником цилиндрической волны.
Пусть лента возбуждается Е-поляризованной волной, создаваемой
нитью электрического тока, текущего вдоль оси ![]() и
проходящего через точку с координатами
и
проходящего через точку с координатами ![]() (рис.
2). Единственную ненулевую составляющую напряженности электрического поля этой
волны запишем в виде
(рис.
2). Единственную ненулевую составляющую напряженности электрического поля этой
волны запишем в виде
где ![]() – амплитудный коэффициент размерности В/м
и
– амплитудный коэффициент размерности В/м
и ![]() – функция Ханкеля второго рода нулевого
порядка.
– функция Ханкеля второго рода нулевого
порядка.
Так как поля и токи в рассматриваемой двумерной задаче не
зависят от ![]() , функция Грина, стоящая в ИУ (4)
превратится в
, функция Грина, стоящая в ИУ (4)
превратится в ![]() , а само уравнение (4) для
эквивалентного тока
, а само уравнение (4) для
эквивалентного тока ![]() , лежащего в плоскости
, лежащего в плоскости ![]() (рис. 2), примет вид
(рис. 2), примет вид
где ![]() ,
, ![]() –
функция Ханкеля второго рода первого порядка,
–
функция Ханкеля второго рода первого порядка,
– x-я
составляющая напряженности падающего магнитного поля и ![]() –
волновое сопротивление свободного пространства.
–
волновое сопротивление свободного пространства.
ИУ (6) будем решать методом
Крылова-Боголюбова [6], соответствующим кусочно-постоянной аппроксимации
искомого тока на ![]() отрезках разбиения ширины ленты
и удовлетворении уравнения (6) в
отрезках разбиения ширины ленты
и удовлетворении уравнения (6) в ![]() точках с координатами
точках с координатами ![]() , где
, где ![]() и
и ![]() . Указанный метод сводит (6) к СЛАУ,
которая решается здесь гауссовским методом исключения с выбором наибольшего
элемента в столбце. После решения СЛАУ рассчитывается невязка выполнения
граничного условия равенства нулю полного электрического поля на верхней и
нижней поверхностях ленты
. Указанный метод сводит (6) к СЛАУ,
которая решается здесь гауссовским методом исключения с выбором наибольшего
элемента в столбце. После решения СЛАУ рассчитывается невязка выполнения
граничного условия равенства нулю полного электрического поля на верхней и
нижней поверхностях ленты
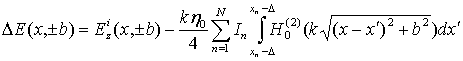 , (8)
, (8)
где
![]() – значение плотности тока на n-м
отрезке.
– значение плотности тока на n-м
отрезке.
Найденный ток также используется для расчета диаграммы рассеяния
определяемой
как поле рассеяния в дальней зоне, нормированное на величину ![]() , где
, где ![]() и
и ![]() – угол, отмеряемый от оси y.
– угол, отмеряемый от оси y.
Результаты, полученные рассматриваемым методом, ниже будут сравниваться с результатами, полученными для бесконечно тонкой ленты и ленты ненулевой толщины с гладкими краями и которые будем называть эталонными.
Плотность тока на тонкой ленте шириной ![]() (рис. 3), возбуждаемой цилиндрической
волной (5), определяется из решения ИУ первого рода
(рис. 3), возбуждаемой цилиндрической
волной (5), определяется из решения ИУ первого рода
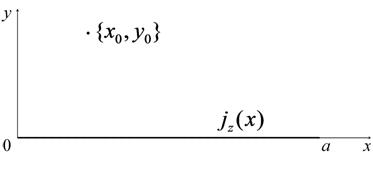
Рис. 3. Плоская бесконечно тонкая лента, возбуждаемая источником цилиндрической волны.
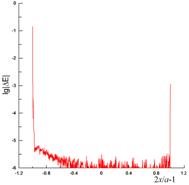
Методы численного решения ИУ (10) хорошо известны. Пример применения метода Крылова-Боголюбова описан в [14], где также приведено выражение для расчета невязки выполнения граничного условия. Диаграмма рассеяния для этой ленты определяется формулой (9).
Лента ненулевой толщины ![]() с шириной плоских участков
с шириной плоских участков ![]() и краями в форме полуокружностей радиуса
и краями в форме полуокружностей радиуса ![]() показана на рис. 4. Задачу рассеяния поля
цилиндрической волны (5) на этой ленте будем решать хорошо известным методом
вспомогательных источников (МВИ) [15].
показана на рис. 4. Задачу рассеяния поля
цилиндрической волны (5) на этой ленте будем решать хорошо известным методом
вспомогательных источников (МВИ) [15].
Рис. 4. Плоская лента конечной толщины с гладкими краями, возбуждаемая источником цилиндрической волны.
Согласно МВИ, поле, рассеянное лентой, представляется в виде суммы цилиндрических волн
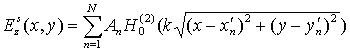 (11)
(11)
с
неизвестными амплитудами ![]() , возбуждаемых нитями
вспомогательного электрического тока, проходящих через точки с координатами
, возбуждаемых нитями
вспомогательного электрического тока, проходящих через точки с координатами ![]() . Указанные точки, обозначенные красными
крестиками на рис. 4, располагаются внутри рассеивателя на ленте толщиной
. Указанные точки, обозначенные красными
крестиками на рис. 4, располагаются внутри рассеивателя на ленте толщиной ![]() с краями в форме полуокружностей радиуса
с краями в форме полуокружностей радиуса ![]() . Неизвестные амплитуды
. Неизвестные амплитуды ![]() определяются из условия равенства нулю
полного электрического поля в
определяются из условия равенства нулю
полного электрического поля в ![]() точках коллокации на
поверхности ленты, которое дает следующую СЛАУ
точках коллокации на
поверхности ленты, которое дает следующую СЛАУ
где
![]() – координаты точек коллокации,
обозначенных синими кружочками на рис. 4, и
– координаты точек коллокации,
обозначенных синими кружочками на рис. 4, и ![]() .
Точность решения задачи контролируется невязкой выполнения граничного условия
.
Точность решения задачи контролируется невязкой выполнения граничного условия
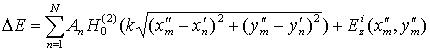 (13)
(13)
в
промежуточных точках коллокации с координатами ![]() ,
обозначенных черными кружочками на рис. 4. Найденные амплитуды
,
обозначенных черными кружочками на рис. 4. Найденные амплитуды ![]() позволяют затем рассчитать поверхностную
плотность тока на ленте по формуле
позволяют затем рассчитать поверхностную
плотность тока на ленте по формуле
![]()
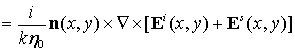 , (14)
, (14)
где
![]() – координаты точки на поверхности ленты и
– координаты точки на поверхности ленты и
![]() – единичный вектор внешней нормали к поверхности,
а также – диаграмму рассеяния
– единичный вектор внешней нормали к поверхности,
а также – диаграмму рассеяния
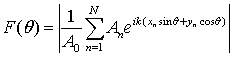 . (15)
. (15)
На рис. 5–7 приведены результаты,
полученные при решении задачи возбуждения бесконечной тонкой ленты шириной a=8λ
при различных положениях источника с использованием ИУ (10) при ![]() , где
, где ![]() В/м
и
В/м
и ![]() . Точность решения характеризуется
невязкой, уменьшение которой при увеличении порядка СЛАУ N
демонстрируется
на рис. 5(а). Плотность тока, найденная из ИУ, сравнивается с плотностью тока,
определенной по методу ФО с использованием (7) при у=0. При x0=4λ
и y0=1.25λ
(рис. 5) края ленты возбуждаются существенно слабее, чем ее середина, и поэтому
плотность ИУ-тока близка к плотности ФО-тока за исключением участков, близких к
краям. При этом диаграммы рассеяния, полученные из ИУ и ФО (рис. 5(в))
практически совпадают.
. Точность решения характеризуется
невязкой, уменьшение которой при увеличении порядка СЛАУ N
демонстрируется
на рис. 5(а). Плотность тока, найденная из ИУ, сравнивается с плотностью тока,
определенной по методу ФО с использованием (7) при у=0. При x0=4λ
и y0=1.25λ
(рис. 5) края ленты возбуждаются существенно слабее, чем ее середина, и поэтому
плотность ИУ-тока близка к плотности ФО-тока за исключением участков, близких к
краям. При этом диаграммы рассеяния, полученные из ИУ и ФО (рис. 5(в))
практически совпадают.
а) б) в)
Рис. 5. Невязка (a),
модуль плотности тока (б) и диаграмма рассеяния (в)
для бесконечно тонкой ленты
с a=8λ при x0=4λ
и y0=1.25λ.
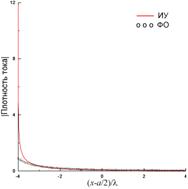
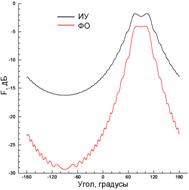
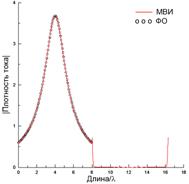
На рис. 6 приведены результаты, соответствующие координатам источника x0=–λ и y0=0.5λ. В этом случае краевой эффект для левого грая ленты проявляется заметно сильнее, чем в предыдущем случае. Так как падение волны на ленту близко к скользящему, ФО-ток близок к нулю (рис. 6(б)), а ИУ-ток имеет резкий максимум у левого края, формирующий краевую волну. Диаграммы рассеяния, полученные из ИУ и ФО и показанные на рис. 6(в), существенно отличаются друг от друга.
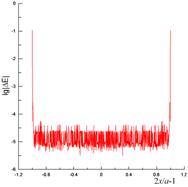
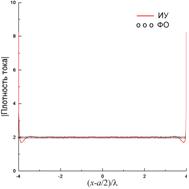
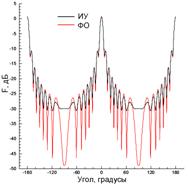
При x0=4λ и y0=50λ (рис. 7) края ленты возбуждаются почти также интенсивно, как и центральная область, что приводит к заметному краевому эффекту для тока (рис. 7(б)), который существенно отличается от ФО-тока у краев, но близок к последнему на большей части ширины ленты. Диаграммы рассеяния для ИУ и ФО (рис. 7(в)) отличаются уровнем заплывания нулей.
а) б) в)
Рис. 6. То же, что и на рис. 5, при N=800, x0=–λ и y0=0.5λ.
а) б) в)
Рис. 7. То же, что и на рис. 5, при N=800, x0=4λ и y0=50λ.
Численные результаты, полученные методом
вспомогательных источников (СЛАУ (12)) для ленты толщиной ![]() , шириной плоских участков
, шириной плоских участков ![]() и с полукруглыми краями (рис. 4), возбуждаемой
так же, как и в предыдущем случае, приведены на рис. 8–10. Рис. 8(а)
характеризует сходимость невязки при увеличении числа N
вспомогательных источников, расположенных на внутренней ленте толщиной
и с полукруглыми краями (рис. 4), возбуждаемой
так же, как и в предыдущем случае, приведены на рис. 8–10. Рис. 8(а)
характеризует сходимость невязки при увеличении числа N
вспомогательных источников, расположенных на внутренней ленте толщиной ![]() . Плотность тока и диаграмма рассеяния,
приведенные на рис. 8(б) и 8(в), соответствуют
. Плотность тока и диаграмма рассеяния,
приведенные на рис. 8(б) и 8(в), соответствуют ![]() . Как
мы видим, краевой эффект при указанном возбуждении проявляется еще слабее, чем
для бесконечно тонкой ленты, из-за отсутствия острых кромок. При этом плотность
тока на освещенной стороне на рис. 8(б) близка к плотности ФО-тока, а диаграмма
рассеяния на рис. 8(в) близка к диаграмме рассеяния для тонкой ленты на рис.
5(в).
. Как
мы видим, краевой эффект при указанном возбуждении проявляется еще слабее, чем
для бесконечно тонкой ленты, из-за отсутствия острых кромок. При этом плотность
тока на освещенной стороне на рис. 8(б) близка к плотности ФО-тока, а диаграмма
рассеяния на рис. 8(в) близка к диаграмме рассеяния для тонкой ленты на рис.
5(в).
а) б) в)
Рис. 8. Невязка (a),
модуль плотности тока (б) и диаграмма рассеяния (в) для ленты,
показанной на рис.
4 с ![]() , a=8λ и
, a=8λ и ![]() при x0=4λ
и y0=1.3λ.
при x0=4λ
и y0=1.3λ.
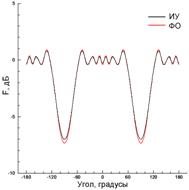
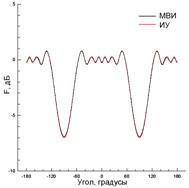
Как и в случае с тонкой лентой, расположение источника вблизи кромки ленты ненулевой толщины краевой эффект проявляется гораздо сильнее даже при сглаженной кромке как показано кривой плотности тока на рис. 9(б). Заметим, что всплеск тока на графике справа на самом соответствует криволинейному участку на левой кромке, так как длина по контуру поперечного сечения ленты отмеряется от начала ее верхнего прямолинейного участка, и левая кромка, таким образом, соответствует значениям длины, находящимся вблизи максимального значения. Ток, рассчитанный по методу ФО и показанный на этом же рисунке, имеет существенное отличие вблизи указанной кромки. Диаграмма рассеяния, показанная на рис. 9(в), имеет некоторое отличие (максимум ~2.5 дБ) от диаграммы для тонкой ленты в угловом секторе вблизи –90°, а диаграмма рассеяния, рассчитанная по методу ФО (рис. 6(в)) имеет более существенные отличия.
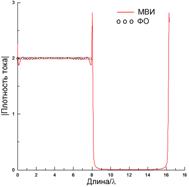
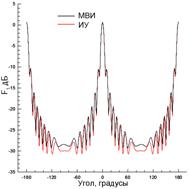
При возбуждении ленты источником, симметрично расположенным над лентой на большом расстоянии 50λ (рис. 10) краевой эффект проявляется в существенных всплесках тока на сглаженных кромках как в [10] и в осцилляциях вблизи них (рис. 10(б)). Диаграмма рассеяния в этом случае (рис. 10(в)) близка к диаграмме рассеяния для тонкой ленты. Небольшое отличие (~1.5 дБ) имеется только в угловых областях вблизи ±90°.
а) б) в)
Рис. 9. То же, что и на рис. 8, при N=1250, x0=–λ и y0=0.5λ.
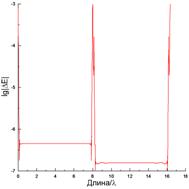
а) б) в)
Рис. 10. То же, что и на рис. 8, при N=1250, x0=4λ и y0=50λ.
Результаты,
полученные при решении ИУ 2-го рода (6), и их сравнение с аналогичными
результатами, полученными другими методами, приведены на рис. 11–13.
Результаты, приведенные на рис. 11, соответствуют ленте шириной ![]() и толщиной
и толщиной ![]() ,
возбуждаемой источником с координатами x0=4λ
и y0=1.3λ,
т.е. случаю, когда края ленты возбуждаются заметно слабее, чем ее центральная
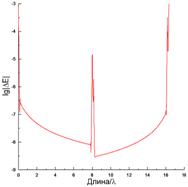
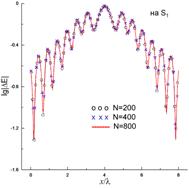
часть. Рис. 11(а) показывает, что невязка выполнения граничного условия для
касательного электрического поля здесь имеет существенно более высокий уровень,
чем для эталонных методов, рассмотренных выше, и может достигать 100%. При этом
никакого уменьшения ее уровня не наблюдается при увеличении числа сегментов
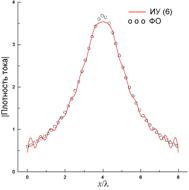
разбиения ленты, т.е. порядка СЛАУ. Плотность тока, найденная из (6) и
показанная на рис. 11(б), довольно близка к плотности ФО-тока, что обусловлено
слабым краевым эффектом, хотя полученная кривая имеет слабые осцилляции,
отсутствующие у токов, полученных эталонными методами и приведенных на рис.
5(б) и 8(б). Диаграмма рассеяния, приведенная на рис. 11(в), в целом также
близка к результатам, полученным по ФО и МВИ, однако имеет отличия около 3 дБ
от эталона в угловых областях вблизи ±90°. Таким образом, даже при слабом
краевом эффекте метод ИУ (6) работает несколько хуже, чем даже метод ФО.
,
возбуждаемой источником с координатами x0=4λ
и y0=1.3λ,
т.е. случаю, когда края ленты возбуждаются заметно слабее, чем ее центральная
часть. Рис. 11(а) показывает, что невязка выполнения граничного условия для
касательного электрического поля здесь имеет существенно более высокий уровень,
чем для эталонных методов, рассмотренных выше, и может достигать 100%. При этом
никакого уменьшения ее уровня не наблюдается при увеличении числа сегментов
разбиения ленты, т.е. порядка СЛАУ. Плотность тока, найденная из (6) и
показанная на рис. 11(б), довольно близка к плотности ФО-тока, что обусловлено
слабым краевым эффектом, хотя полученная кривая имеет слабые осцилляции,
отсутствующие у токов, полученных эталонными методами и приведенных на рис.
5(б) и 8(б). Диаграмма рассеяния, приведенная на рис. 11(в), в целом также
близка к результатам, полученным по ФО и МВИ, однако имеет отличия около 3 дБ
от эталона в угловых областях вблизи ±90°. Таким образом, даже при слабом
краевом эффекте метод ИУ (6) работает несколько хуже, чем даже метод ФО.
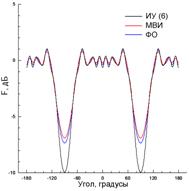
а) б) в)
Рис. 11. Невязка (a),
модуль плотности тока (б) и диаграмма рассеяния (в) для ленты,
показанной на рис.
2 с ![]() и a=8λ при x0=4λ
и y0=1.3λ.
и a=8λ при x0=4λ
и y0=1.3λ.
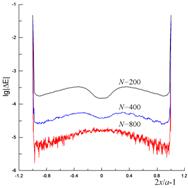
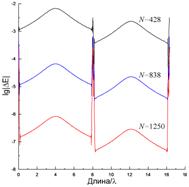
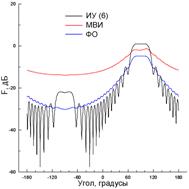
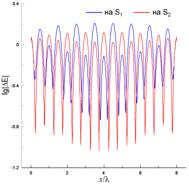
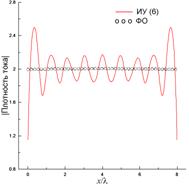
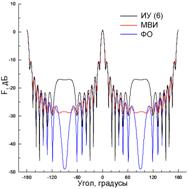
Рис. 12 и 13 содержат результаты, полученные с использованием (6) при возбуждении ленты источником с координатами x0=–λ и y0=0.5λ (рис. 12) и x0=4λ и y0=50λ (рис. 13) при N=800. Как и в предыдущем случае, невязка выполнения граничного условия для касательного электрического поля (рис. 12(а) и 13(а)) может достигать 100% и даже выше, что говорит о фактическом неудовлетворении указанного граничного условия. Распределения тока, полученные в результате решения ИУ (6) и показанные на рис. 12(б) и 13(б), как качественно, так и количественно существенно отличаются и от ФО-тока, и от токов, полученных эталонными методами и показанными на рис. 6(б), 9(б), 7(б) и 10(б). Ни о какой способности учитывать краевые эффекты с использованием (6) в рассматриваемых случаях говорить не приходится. При этом распределения тока, полученные из (6), существенно отличаются от эталонных токов не только у краев ленты, но и в ее центральной части. В результате, полученные ошибочные распределения токов дают существенные ошибки в вычислении диаграмм рассеяния, показанных на рис. 12(в) и 13(в). Особенно показательны результаты на рис. 13(в), где уровень ДН, полученный на основе (6), отличается более чем на 10 дБ от эталонной диаграммы в довольно широкой боковой области углов.
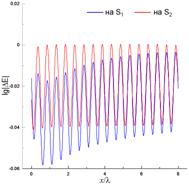
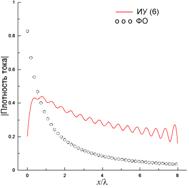
а) б) в)
Рис. 12. То же, что и на рис. 11, при N=800, x0=–λ и y0=0.5λ.
а) б) в)
Рис. 13. То же, что и на рис. 10, при N=800, x0=4λ и y0=50λ.
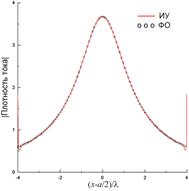
Наконец,
на рис. 14 проводится сравнение результатов для плотности тока и диаграммы
рассеяния, полученных методом ИУ 2-го рода (6), МВИ и методом ИУ 1-го рода (10)
для сравнительно узкой ленты с ![]() , возбуждаемой
источником с координатами x0=0.5λ
и y0=50λ,
т.е. фактически плоской волной при нормальном падении. Толщина ленты для ИУ (6)
и МВИ равна
, возбуждаемой
источником с координатами x0=0.5λ
и y0=50λ,
т.е. фактически плоской волной при нормальном падении. Толщина ленты для ИУ (6)
и МВИ равна ![]() . Толщина внутренней ленты, на которой
располагаются вспомогательные источники в МВИ (рис. 4) равна
. Толщина внутренней ленты, на которой
располагаются вспомогательные источники в МВИ (рис. 4) равна ![]() . Число неизвестных равно N=100 в
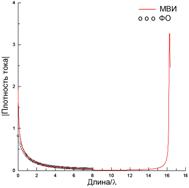
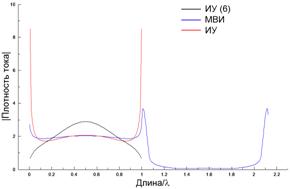
методах ИУ (6) и (10) и N=206 в МВИ. Как показывает сравнение, поведение
распределения тока, полученного из ИУ (6), кардинально отличается от поведения
распределений, полученных эталонными методами (рис. 14(а)), что приводит к
существенным ошибкам в расчетах диаграммы рассеяния по сравнению с эталонными
диаграммами (рис. 14(б)).
. Число неизвестных равно N=100 в
методах ИУ (6) и (10) и N=206 в МВИ. Как показывает сравнение, поведение
распределения тока, полученного из ИУ (6), кардинально отличается от поведения
распределений, полученных эталонными методами (рис. 14(а)), что приводит к
существенным ошибкам в расчетах диаграммы рассеяния по сравнению с эталонными
диаграммами (рис. 14(б)).
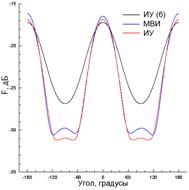
а) б)
Рис. 14. Сравнение распределений тока (a), и диаграмм рассеяния (б) для ленты шириной a=λ при x0=0.5λ и y0=50λ.
4. Выводы
Аналитический и численный анализ ИУ 2-рода (4) и (6), выведенные согласно подходу, предложенному в [3] для анализа протяженных проводящих рассеивателей малой, но ненулевой толщины, позволяет сделать следующие выводы.
Как показано аналитически на примере плоского рассеивателя, указанный подход, так же, как и метод ФО, не позволяет учесть краевые эффекты, проявляющиеся в формировании краевых волн и появлении кроссполяризационной составляющей плотности тока. Так как обе составляющие тока влияют друг на друга, то неспособность учета кроссполяризации приводит к ошибкам при расчете плотности тока на основной поляризации.
Численное моделирование в двумерном случае показало, что подход, предложенный в [3], может давать сравнительно близкие к эталонным результаты только при слабом краевом эффекте, когда простой метод ФО также дает результаты, еще более близкие к результатам, полученным эталонными численными методами. В этих случаях слабых краевых эффектов никаких численных методов не требуется, и применение подхода [3] было бы просто напрасной тратой компьютерных ресурсов.
В случаях заметных краевых эффектов, подход [3] дает результаты для плотности тока, существенно отличающиеся от результатов, полученных эталонными методами. Как следствие, возникают заметные ошибки в вычислении диаграмм рассеяния. В этих случаях подход [3], основанный на эквивалентном токе, просто не работает.
Литература
1. Бутенко В. В., Бузова М. А. Вопросы электродинамического анализа слабо искривленных тонких протяженных рассеивателей. // Труды НИИР. – 2011. – №3. – С. 48-52.
2. Бузова М. А. Электродинамический анализ эклектичных антенных систем // Радиотехника. – 2011. – №11. – С. 55-59.
3. Бузова М. А. Электродинамический анализ поверхностных рассеивателей конечной толщины с помощью интегрального уравнения второго рода относительно эквивалентного тока. // Физика волновых процессов и радиотехнические системы. – 2011. – Т. 14. – №4. – С. 68-76.
4. Бузова М. А. Методы электродинамического моделирования эклектичных антенных систем. // Журнал радиоэлектроники: электронный журнал. 2012. – №4. – URL: http://jre.cplire.ru/jre/apr12/4/text.pdf
5. Jacobus U., Landstorfer F. M. Improved PO-MM hybrid formulation for scattering from three-dimensional perfectly conducting bodies of arbitrary shape. // IEEE Trans. Antennas Propagat. – 1995. – V.43. – №2. – P. 162-169.
6. Васильев Е. Н. Возбуждение тел вращения. – М.: Радио и связь, 1987.
7. Бузова М. А., Юдин В. В. Исследование вопросов сокращения вычислительных ресурсов при использовании интегральных уравнений второго рода для анализа эклектичных антенных систем. // Радиотехника. – 2012. – №6. – С. 82-86.
8. Бузова М. А. Некоторые свойства ядер уравнений Фредгольма второго рода. // Вестник Самарского гос. тех. ун-та. Сер. Физ-мат. науки. – 2011. – №1. – С. 28-33.
9. Миттра Р., Ли С. Аналитические методы теории волноводов. – М.: Мир, 1974.
10. Andreasen M. G. Scattering from parallel metallic cylinders with arbitrary cross sections. // IEEE Trans. Antennas Propagat. – 1964. – V. 12. – №6. – P. 746-754.
11. Скобелев С. П. Замечания по статье "Вопросы электродинамического анализа слабо искривленных тонких протяженных рассеивателей". // Труды НИИР. – 2012. – №4. – С. 69-71.
12. Rahmat-Samii Y., Mittra R. Integral equation solution and RCS computation of a thin rectangular plate. // IEEE Trans. Antennas Propagat. – 1974. – V. 22. – №4. – P. 608-610.
13. Медведик М. Ю., Смирнов Ю. Г., Соболев С. И. Параллельный алгоритм расчета поверхностных токов в электромагнитной задаче дифракции на экране. // Вычислительные методы и программирование. – 2005. – Т. 6. – №1. – С. 99-108.
14. Скобелев С. П. О применении продолженных граничных условий и вейвлетов Хаара в задачах рассеяния волн тонкими экранами. // Радиотехника и электроника. – 2006. – Т. 51. – №7. – С. 796-806.
15. Малакшинов Н. П., Ерихов В. Г. Об одном численном методе решения задач дифракции. // Антенны. – 1977. – Вып. 25. – С. 53-65.