УДК 621.396, 621.391

ОЦЕНКА ВЛИЯНИЯ БАЗЫ ХАОТИЧЕСКИХ РАДИОИМПУЛЬСОВ НА ДАЛЬНОСТЬ СВЯЗИ В СВЕРХШИРОКОПОЛОСНОЙ ПРИЕМОПЕРЕДАЮЩЕЙ СИСТЕМЕ

 

М. Г. Попов

Институт радиотехники и электроники им. В.А. Котельникова РАН,
Московский физико-технический институт

Статья получена 20 мая 2014 г.

Аннотация. В работе исследуется влияние базы сигнала на дальность передачи данных в системе связи с некогерентным приемом, использующей в качестве носителя информации хаотические радиоимпульсы. Рассчитываются количественные зависимости между базой сигнала и дальностью связи в свободном пространстве, анализируется возможность практического использования этих зависимостей.

Ключевые слова: прямохаотические системы связи, дальность передачи, сверхширокополосные системы связи.

Abstract: In the paper impact of signal base upon distance of data transmission in the noncoherent transmission system with carrier based on chaotic radio pulses was analyzed.  Quantative assesments of relationship between signal base and distance of transmission in lacunar space was made. Possibility of practical application was analyzed.

Key words: chaotic communication, ultrawideband communication systems, transmission distance.

 

Введение

Сверхширокополосные (СШП) системы связи привлекают большое внимание исследователей и промышленности с начала 2000 годов, когда в ряде стран были приняты решения об их нелицензируемом использовании [1,2]. Во избежание интерференции с обычными узкополосными радиосистемами, принятые решения накладывают жесткие ограничения на спектральную плотность мощности излучаемых СШП сигналов. Так в США она не должна превышать -41.3 дБм/МГц, а в России ограничения еще жестче - -45,0 дБм/МГц и ниже в зависимости от диапазона. Это означает, что дальность действия нелицензируемых СШП систем лежит в пределах от единиц до десятков метров,

Но каков теоретический и практический предел дальности передачи в СШП нелицензируемых средствах связи?

Ясно, что он зависит от таких факторов как полоса излучаемого сигнала (не менее 500 МГц) и скорость передачи данных. Первый фактор определяет вместе с ограничениями на спектральную плотность максимально допустимую интегральную мощность излучения, второй, вместе с допустимой мощностью излучения, -  максимально возможную энергию излучаемого сигнала на бит передаваемой информации – E_b. Поскольку многие типы сверхширокополосных сигналов являются импульсными, то в принципе можно неограниченно наращивать энергию импульса за счет снижения числа импульсов, излучаемых в единицу импульсов. Однако это может приводить к нежелательной интерференции с другими типами электронной аппаратуры. Поэтому для нелицензируемых СШП систем введено также ограничение на пиковую излучаемую мощность: в зоне максимальной спектральной плотности сигнала, в полосе 50 МГц пиковая мощность не должна превышать 0 дБм [1].

Таким образом, задача о максимальной дальности передачи СШП системы связи должна решаться с учетом указанных обстоятельств. Еще одна группа факторов, которая будет влиять на получаемые оценки, определяется типом используемых сигналов, методами модуляции и демодуляции. Число типов СШП сигналов реально и потенциально пригодных для СШП связи уже сейчас превышает десяток [3]. В даннгой работе рассматривается только один тип СШП сигналов – хаотические сигналы и рассматривается только прямохаотическая система связи. При этом в качестве метода модуляции будет использована ‘on – off” модуляция, а в качестве метода демодуляции – некогерентный энергетический прием.

Структура статьи следующая.

В первом разделе описывается модель система связи и предшествующие данной работе результаты по оценке ее характеристик.

Во втором разделе представлена методика исследования и схема моделирования.

Третий раздел посвящен расчетам и анализу их результатов.

 1. Состояние вопроса

В основу прямохаотических схем связи заложены три базовые идеи [4-8, 9]:

1) источник хаоса генерирует хаотические колебания непосредственно в заданной полосе СВЧ диапазона; 2) ввод информационного сигнала в хаотический осуществляется путем формирования соответствующего потока хаотических радиоимпульсов; 3) извлечение информации производится из СВЧ хаотического сигнала без промежуточного преобразования частоты.

Структура прямохаотической системы связи в случае канала с белым шумом показана на рис. 1.

 

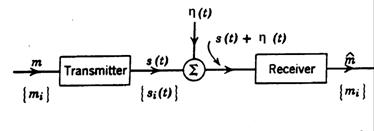
Рис.1. Модель передачи сигнала

 

Передатчик системы состоит из устройства управления генератором, источника хаоса, генерирующего сигнал непосредственно в частотном диапазоне передачи информации, т.е. в области радио или сверхвысоких частот, модулятора ключевого типа, усилителя, антенны, источника информации, кодера источника и кодера канала.

Передатчик обеспечивает формирование содержащего информацию сигнала в полосе частот

DF = F_в - F_н,                                                                                                 (1)

где F_н и F_в – нижняя и верхняя границы полосы частот хаотических колебаний.

Передатчик включает в себя модулятор, который осуществляет формирование хаотических радиоимпульсов и интервалов между импульсами.

В случае “on – off” модуляции формирование потока осуществляется при фиксированной частоте следования позиций для импульсов и при фиксированной длительности импульсов. Наличию импульса на заданной позиции в потоке соответствует передаваемый символ “1”, а отсутствию импульса - символ “0”. Передача информации осуществляется путем формирования потока хаотических радиоимпульсов. При этом длина каждого импульса равна τ, а продолжительность временного окна, на котором располагается позиция под радиоимпульс – T. Параметр

                                                                                                                                         (2)

будем называть скважностью передачи битов.

Пусть P – мощность исходного хаотического сигнала и при передаче информации «1» кодируется наличием хаотического радиоимпульса на отведенной позиции, а «0» его отсутствием. Тогда средняя мощность хаотического сигнала в канале связи будет равна

.                                                                                                     (3)

Базой сигнала называется величина [10,11]

.                                                                                                     (4)

В зависимости от значения базы B различаются элементарные сигналы с базой

                                                                                               (5)

и сложные сигналы, для которых справедливо соотношение

B =                                                                                              (6)

Если длительность хаотического радиоимпульса τ >> 1/(2ΔF), то спектр мощности потока хаотических радиоимпульсов практически не будет отличаться от спектра мощности исходного хаотического сигнала. Поскольку величина 2τΔF представляет собой базу сигнала, то увеличение длины хаотического радиоимпульса приводит к увеличению базы сигнала.

Применение хаотических радиоимпульсов в качестве носителей информации позволяет создавать различные системы сигналов для организации некогерентного и когерентного приёма. Энергетическая эффективность использования некоторых из них рассмотрена в работах [12]. В частности, в них рассмотрена и эффективность схемы некогерентного приема при использовании “on – off” модуляции. Ниже результаты этих работ будут использованы при оценке предельной возможной дальности прямохаотической системы связи.

Пусть  и  - образы сигнала, которые соответствуют двум разным передаваемым символам. В нашем случае S₀(t)=0, S₁(t) - хаотический радиоимпульс. На вход устройства обработки поступает сигнал y(t)

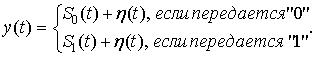                                                     (7)

 

где  - гауссовский шум, со спектральной плотностью N₀.

При некогерентном приеме обработка сигнала заключается в его детектировании с помощью квадратичного детектора, интегрировании на интервале времени t, и сравнении с пороговым значением (рис. 4а). На пороговое устройство поступает сигнал

d₀ = ,

 

если передается символ «0» и сигнал

d₁ = ,

 

если передается символ «1».

Решение о приеме «0» или «1» принимают исходя из сравнения получаемого значения d_i с порогом  d. Если d_i < d, то считается, что поступил символ «0», в противном случае – символ «1».

Анализ помехоустойчивости ПХСС может быть проведен как с использованием непрерывной модели, рассмотренной выше, так и с использованием дискретизации сигнала по времени. В этом случае сигналы S₀(t) и S₁(t) заменяются на сигналы S₀(i) и S₁(i), а шум η(t) на шумовые отсчеты η(i), где , ,

Считается, что полоса фильтра согласована с полосой хаотического сигнала. Поэтому шумовой сигнал имеет то же время корреляции и ту же полосу что и хаотический.

В дискретном варианте основные для некогерентного приема будут выглядеть следующим образом.

 - если передается символ «0».

-если передается символ «1».

Проблема при некогерентном приеме, в дискретном случае, так и в непрерывном состоит в том, что сравнивать d₀ и d₁ приходится не друг с другом, а каждое с пороговым значением, которое оценивается отдельно и вносит дополнительную неопределенность.

 Отличительной особенностью ПХСС является то, что в них возможно относительно простое варьирование базы сигнала и тем самым в широких пределах менять величину энергии сигнала на бит, не выходя за ограничения, накладываемые на нелицензируемые системы спектральной плотности и пиковой мощности.

Действительно, увеличение базы сигнала за счет увеличения длительности импульса при постоянной мощности импульса и соответстствующем уменьшении числа импульсов в единицу времени (уменьшения скорости передачи) оставляет постоянной  среднюю излучаемую мощность. С другой стороны при этом не растет и пиковая мощность.

При выборе порогового значения энергии будем использовать критерий максимально правдоподобия (рис. 2) [4]. Согласно этому критерию, решения принимаются таким образом, чтобы значения априорных вероятностей ошибкой первого и второго были одинаковыми. В рассматриваемой системе, ошибками первого рода называют ошибку принятия единицы за нуль, а ошибкой второго рода – принятие нуля за единицу. Вероятности ошибки в данном случае соответствуют отмеченным площадям под графиками распределений.

 

 

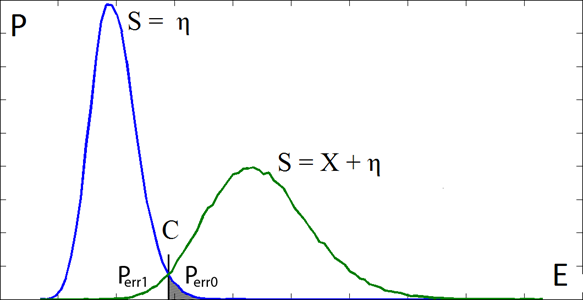
Рис.2. Распределение плотностей вероятностей для энергий шума и сигнала с шумом.

 

2. Схема моделирования

Расчет статистических характеристик системы передачи производился по следующей схеме.

Для выбора порога энергии, детектирование которого соответствует принятию единицы, генерировалась калибровочная последовательность вида 0101010101... Далее, эта последовательность смешивалась с гауссовским шумом и строились распределения плотностей вероятностей — шум и сигнал+шум(рис). В соответствии с полученными распределениями выбиралось пороговое значение сигнала, как точки пересечения двух распределений (рис 2). Такой выбор порога достаточного точно соответствует критерию максимального правдоподобия.

После этого, для определения зависимости вероятности ошибок при различных значениях E_b/N₀, можно моделировать процесс передачи соответствующего числа бит. Однако, такой подход возможен только для сигналов с небольшой базой. Задача моделирования непосредственной передачи случайной последовательности бит для сигналов с большой базой, которые рассматриваются в данной работе, требует других подходов. В наших расчетах оценка вероятностей ошибок на бит производилась по заранее рассчитанным распределениям энергий на импульс, что требует существенно меньшего объема вычислений. В использованном подходе вероятность ошибки на бит определяется согласно соотношениям:

 

,  ,                                                                  (8)

 

гдеи– вероятности появления нуля и единицы, аи– вероятности принять нуль за единицу и единицу за нуль соответственно. Вероятностии определяются путем интегрирования плотности вероятности (рис. 2) от значения 0 до определяемого порогового значения (), и от искомого порогового значения до бесконечного ().  Результаты расчетов приведены на рис. 3.

 

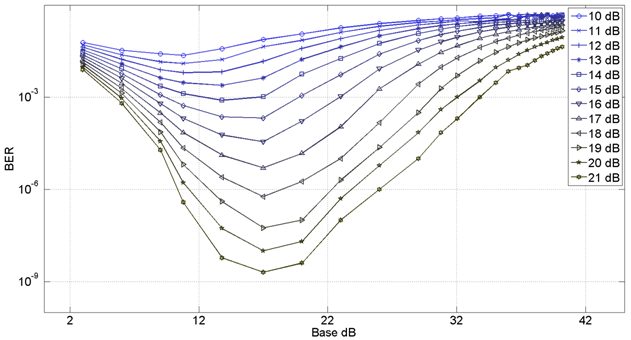
а)

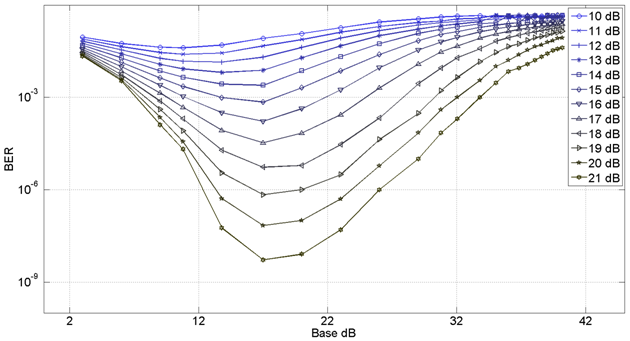
б)

Рис. 3. Вероятность ошибки на бит в зависимости от базы сигнала: а) для равномерного распределения; б) для гауссовского распределения

 

При использовании метода оценки вероятности ошибки при помощи заранее рассчитанных распределений, были проведены расчеты, как для   малых, так и для больших значений базы. Расчеты при малых значениях базы позволили убедиться в том, что получаемые результаты согласуются с результатами непосредственного моделирования с помощью случайных последовательностей битов. Из проведенных расчетов следует, что метод оценки вероятностей ошибок по распределениям является менее точным, чем прямое моделирование. Тем не менее, он позволяет вычислять вероятности с точностью ~10^-6, что вполне достаточно для целей данной работы.

 

3. Зависимость дальности связи от базы хаотического радиоимпульса

Дальность передачи R представляет собой расстояние между передатчиком и приемником, при котором достигается максимально допустимая вероятность ошибки на бит. Она, в свою очередь зависит от отношения K = . – энергии на бит на входе приемника к спектральной плотности теплового шума.  В свободном пространстве величина К связана с дальностью передачи соотношением [4]:

 ,                                                                                         (9)

 

 

где  – эффективная площадь приемной антенны, - мощность излучающего передатчика, τ –  длина импульса, D – скважность. Двойка в знаменателе появляется за счет того, что средняя излучаемая энергия на бит вдвое меньше энергии, излучаемой в импульсе, в силу используемой при модуляции “on – off” системы сигналов. Соотношение (9) может быть переписано с использованием базы сигнала как параметра

 .                                                                                     (10)

 

                                                          

В случае элементарных сигналов c B ~ 1  и при когерентном приеме сложных сигналов с B > 1 вероятность ошибки на бит определяется только величиной K. При прочих фиксированных условиях это означает, что . Однако, в системах передачи на хаотических радиоимпульсах, энергетического приема вероятность ошибки при фиксированном значении K зависит от базы сигнала, следовательно, и дальность передачи не растет как .

Определение зависимости дальности передачи от базы хаотического сигнала при некогерентном приеме производилось в несколько последовательных этапов. Первоначально были рассчитаны зависимости для вероятностей ошибок при фиксированных значениях E_b/N₀ и изменяющейся базе сигнала. База при этом варьировалась от 3 дБ до 40.2 дБ. Полученные кривые показаны на рис 3. При этом, стоит отметить падение эффективности энергетического приема при увеличении базы сигнала.

Следующим этапом был расчёт требуемого уровня E_b/N₀ при фиксированном уровне ошибок в зависимости от базы сигнала (рис. 4). Форма этого уровня определяется двумя факторами. Во-первых, большим разбросом энергии от импульса к импульсу при малых базах даже при больших значениях отношения E_b/N₀, когда влиянием теплового шума на флуктуацию энергии импульса можно пренебречь и, во-вторых, уменьшением эффективности приема с ростом базы.

 

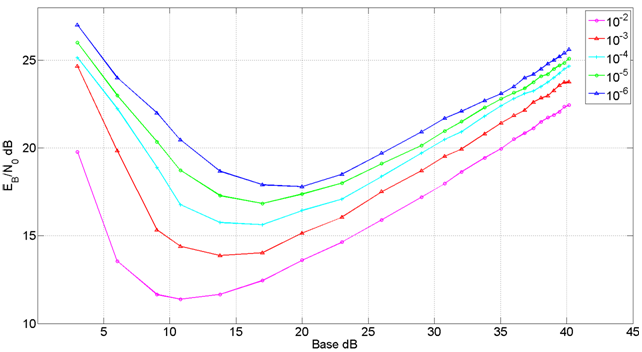
Рис. 4. Зависимость E_b/N₀ от базы сигнала при фиксированных значениях вероятности ошибки

 

На последнем этапе рассчитывались собственно зависимости дальности передачи от базы сигнала для фиксированных вероятностей ошибки на бит (BER). Эти зависимости представлены на рис. 5.

Из приведенных графиков видно, что дальность передачи монотонно растет с увеличением база сигнала. При этом увеличение дальности замедляется  по отношению к соответствующему росту базы для больших баз сигнала. Так увеличение базы в два раза (на 3 дБ) приводит к увеличению дальности:

- для начальной базы 10 дБ на 2.5 дБ;

- для начальной базы 25 дБ на 1.1 дБ;

- для начальной базы 35 дБ на 1 дБ.

При этом прирост дальности передачи с увеличением базы сигнала практически одинаков для всех кривых на рис. 5, т.е. независим от вероятности ошибок.

 

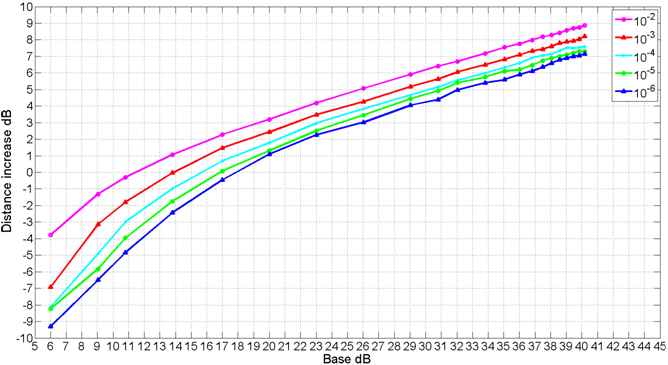
Рис. 5. Зависимости дальности передачи от базы сигнала для фиксированного уровня BER

Пусть, например, прямохаотический приемопередатчик обеспечивает дальность передачи в режиме «точка – точка» в 25 м при базе сигнала порядка 17 дБ и BER = 10^-6. Если оставлять требования к уровню ошибок неизменными, то для увеличения дальности передачи с 25 до 50 метров потребуется увеличить базу сигнала в 5.5 раз. При увеличении базы сигнала в 2 раза, происходит увеличение предельной дальности с 25 метров до 32 метров.

При анализе реальных устройств, учитывая прямую связь базы со скоростью передачи, часто удобно рассматривать дальности передачи как функцию ее скорости. Так для сверхширокополосных прямохаотических  приемопередатчиков ППС-43 [10], при фиксированной вероятности ошибки   10^-6 дальность передачи дальность передачи составляет 20 м при скорости передачи 6 Мбит/сек, а уменьшение скорости до 250 кБит/сек позволяет увеличить дальность до 60 метров.

4. Заключение

В работе исследовано влияние базы сигнала на дальность передачи данных в системе связи с некогерентным приемом, использующей в качестве носителя информации хаотические радиоимпульсы. Получены количественные зависимости между базой сигнала и дальностью связи в свободном пространстве, проанализирована возможность практического использования этих зависимостей. Показано, что при значительном увеличении базы сигнала и соответствующем снижении скорости передачи возможно увеличение дальности передачи до трех раз при практически неизменной аппаратной части приемопередатчиков.

 

Литература

1.       Revision of part 15th Commission’s Rules Regarding Ultra-Wideband Transmission Systems, First Report and Order. ET Docket 98–153, FCC 02-48; April 22, 2002. Wash.: Federal Communications Commission (FCC), 2002. // [Электронный ресурс]. URL:
http://hraunfoss.fcc.gov/edocs_public/at-tachmatch/FCC-02-48A1.pdf.

2.       О результатах работ по конверсии радиочастотного спектра по вопросу использования полосы радиочастот 2,85-10,6 ГГц сверхширокополосными беспроводными устройствами. Решение ГКРЧ № 09-05-02 от 15 декабря 2009 г.

3.       Андреев Ю.В., Дмитриев А.С., Кузьмин Л.В., Мохсени Т.И. «Сверхширокополосные сигналы для беспроводной связи» // Радиотехника, 2008, №8, с. 83–90.

4.       Дмитриев А. С., Кяргинский Б. Е., Максимов Н. А., Панас А. И., Старков С. О. // Прямохаотическая передача информации в СВЧ диапазоне. / Препринт ИРЭ РАН № 1(625), Москва, 2000.

5.       Дмитриев А. С., Кяргинский Б. Е., Панас А. И., Старков С. О. // РЭ. 2001. Т. 46. № 2. С. 224.

6.       Dmitriev A.S., Panas A..I., Starkov S.O. // Nonlinear Science Preprint. Nlin.CD/0110047). 2001.

7.       Дмитриев А. С., Кяргинский Б. Е., Панас А. И., Пузиков Д.Ю., Старков С. О. // РЭ. 2002. Т. 47. № …. С. ….

8.       Dmitriev A.S., Kyarginsky B.Ye., Panas A..I., Starkov S.O. // Int. J. of Bifurcation and Chaos. 2003. V. 13. N 8. P. 2024.

9. Дмитриев А.С., Ефремова Е.В., Лазарев В.А., Герасимов М.Ю. «Сверхширокополосная беспроводная самоорганизующаяся прямохаотическая сенсорная сеть» // Успехи современной радиоэлектроники, 2013, №3, с. 19-29.

10. Петрович Н.Т., Размахнин М.К. Системы связи с шумоподобными сигналами. М.: Советское радио, 1969.

11. Варакин Л. Е. Теория сложных сигналов. М.: Советское радио, 1970.

12. Дмитриев А.С., Захарченко К.В., Пузиков Д.Ю. Введение в теорию прямо-хаотической передачи информации // Радиотехника и электроника, 2003, т. 48, № 3, с. 328

13. Б. Скляр. Цифровая связь. Теоретические основы и практическое применение, 2 изд., М.: «Вильямс», 2007. 1104 с.