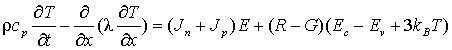УДК 621.382

ОБ ОЦЕНКЕ МОЩНОСТИ ТЕПЛОВОГО ПОРАЖЕНИЯ ДИОДНЫХ
ПОЛУПРОВОДНИКОВЫХ СТРУКТУР ИМПУЛЬСНЫМ
ЭЛЕКТРОМАГНИТНЫМ ИЗЛУЧЕНИЕМ

 

С.А. Мещеряков

Федеральное автономное учреждение "Государственный научно-исследовательский испытательный институт проблем технической защиты информации ФСТЭК России"

 

Статья получена 9 июня 2014 г.

 

Аннотация. В рамках численной модели в диффузионно-дрейфовом тепловом приближении приведены результаты расчета энергомощностных характеристик для p – n-переходной структуры и структуры с барьером Шоттки при воздействии импульсного электромагнитного излучения. Показано различие в оценке мощности теплового поражения по двум критериям: падающей внешней мощности и рассеиваемой внутренней мощности. Проведено сравнение энергомощностных характеристик теплового поражения диодных структур для сверхвысокочастотного и прямоугольных импульсов в диапазоне температур теплового разогрева 400...1400 °С.

Ключевые слова: численная модель, полупроводниковая структура, импульсное излучение, мощность теплового поражения.

Abstract: Within the limits of numerical model in drift-diffusion thermal approach of calculation of power characteristics for p-n-structure and structure with a Schottky barrier are given at action of a pulsing electromagnetic radiation are given. Distinction is shown in an estimate of thermal defeat power by two criterions – incident exterior power and diffused interior power. Characteristics of thermal burnout of the diode-structures for microwave and square pulses in a gamut of temperatures of a thermal heating 400 ... 1400 °С is compare.

Key words: numerical model, semiconductor structure, pulse radiation, power of thermal burnout.

 

Введение

Анализ экспериментальных данных [1 – 8] по влиянию импульсного электромагнитного излучения (ЭМИ) на однотипные полупроводниковые диоды показывает существенную разницу в оценках мощности (энергии) их теплового поражения, составляющую свыше двух порядков при одинаковых длительности и форме воздействующего импульса. Однако геометрические размеры этих полупроводниковых диодов, а значит и подверженный разогреву объем структуры (или ее части) не имеют столь существенного разброса. В рамках распространенных тепловых моделей [2, 9, 10], основанных на рассмотрении только падающей мощности и трактующих всю поступающую "извне" энергию как тепловую и полностью поглощаемую полупроводниковой структурой, объяснить указанную разницу в оценке мощности теплового поражения весьма затруднительно.

В отличие от тепловых моделей представленный в [11 – 15] подход к расчету влияния ЭМИ на полупроводниковые диодные структуры основан на рассмотрении наведенного (на штатные или случайные антенны) или непосредственно поданного в схему измерения электрического сигнала. Под воздействием сигнала ток внутри структуры приводит к возникновению тепловых процессов, влияющих на динамику саморазогрева структуры, и, как следствие, к функциональным сбоям в работе или необратимому тепловому поражению (выгоранию). Указанная трансформация – "воздействующая мощность – электрический сигнал – рассеиваемая мощность" – приводит к необходимости использования двух критериев оценки мощности. Первый критерий должен характеризовать рассеиваемую внутри структуры и приводящую к тепловому разогреву электрическую мощность, связанную с процессами зарядо- и теплопереноса. Второй критерий должен определять необходимую для разогрева внешнюю падающую мощность, зависящую как от рассеиваемой мощности внутри структуры, так и от характеристик приемного тракта аппаратуры, генератора или схемы измерения. Иными словами, первый критерий характеризует энергию (мощность), разогревающую структуру "изнутри", второй – энергию, обеспечивающую этот разогрев "извне".

Цель данной работы – продемонстрировать различие в указанных критериях оценки мощности и энергии теплового поражения импульсом ЭМИ при помощи модели, основанной на диффузионно-дрейфовом тепловом приближении (ДДМТ), на примере диодных структур: биполярной (p – n-переходной) и структуры с барьером Шоттки.

 

Постановка задачи

Вычисления будем проводить для p – n-переходной структуры и структуры с барьером Шоттки на основе кремния в рамках одномерной ДДМТ. Электрофизические параметры кремния (подвижности свободных носителей заряда, теплопроводность и др.) и их температурные зависимости взяты из [16].

На рис. 1а представлен профиль распределения легирующей примеси N(x) в биполярной n⁺ – p – p⁺ – p⁺⁺-диодной структуре. К n⁺-эмиттеру примыкает теплоизолированный омический контакт (), к p⁺⁺-области – омический теплоотводящий контакт (T = T₀ = 20 ºС). Площадь эмиттерного контакта
S = 6.2×10^-6 см².

Рис. 1б иллюстрирует профиль распределения легирующей примеси N(x) в диодной n – n⁺ – n⁺⁺-структуре с барьером Шоттки. К эпитаксиальной пленке n-типа примыкает теплоизолированный выпрямляющий контакт Шоттки с высотой потенциального барьера F_b = 0.7 эВ, к n⁺⁺-области – омический теплоотводящий контакт. Площадь выпрямляющего контакта Шоттки S = 7.5×10^-6 см².

Исходное значение сопротивления обеих структур при указанных параметрах составляет 250 Ом, что соответствует типовым значениям выходного сопротивления СВЧ-диодов [17].

 Не приводя весь набор уравнений ДДМТ (см., например, [14]), требуемый для расчетов электротепловых характеристик полупроводниковой структуры, выделим уравнение теплопроводности, используемое при оценке внутренних рассеиваемых мощности и энергии

 

    

(а)                                                            (б)

Рис. 1. Профили легирующей примеси диодных структур и типы проводимости различных областей (n – электронный, p – дырочный);
а – биполярная структура, б – структура с барьером Шоттки.

 

 

 ,                     (1)

 

где r – плотность вещества; c_p – удельная теплоемкость вещества; T – абсолютная температура; l – коэффициент теплопроводности полупроводника; J_n, J_p – плотность тока электронов и дырок соответственно; E – напряженность электрического поля; R – темп рекомбинации; G – темп генерации; E_c, E_v – энергетические уровни дна зоны проводимости и потолка валентной зоны соответственно; k_B – постоянная Больцмана.

Из уравнения (1) следует, что рассеиваемая мощность, приводящая к изменению температурного поля в каждой точке структуры, связана с тремя электрическими процессами: разогрев протекающим внутри структуры током (Джоулево тепло), выделение дополнительного тепла за счет рекомбинации и поглощение тепла за счет генерации.

Интегрирование по длине моделируемой структуры правой части уравнения (1) дает мгновенную рассеиваемую плотность мощности P(t). Энергия W, рассеиваемая за время импульса t_p, и средняя рассеиваемая мощность P_av за время импульса вычисляются по следующим формулам:

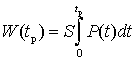,                                                                                     (2)

.                                                                                 (3)

 

Внешняя падающая мощность P_inc (с учетом сопротивления приемной антенны или генератора R и амплитуды или уровня наведенного электрического сигнала U₀) и соответствующая ей энергия W_inc определяются из уравнений

 

,                                                                                                    (4)

 

где  в случае сверхвысокочастотного (СВЧ) импульса и  в случае прямоугольного импульса;

.                                                                                                      (5)

 

Уравнения (2) – (5) иллюстрируют разницу в подходе к оценке энергомощностных характеристик воздействия импульса ЭМИ на исследуемые структуры по критериям внешней падающей мощности и внутренней рассеиваемой мощности. Как следует из уравнения (4), внешняя падающая мощность P_inc складывается из двух компонентов. Первое слагаемое характеризует мощность, рассеиваемую на активном сопротивлении антенного тракта (генератора, схемы измерения и др.), второе – мощность, рассеиваемую на диодной структуре.

"Общей точкой", связывающей представленные характеристики, служит временная зависимость напряжения наведенного сигнала u(t) с амплитудой (или уровнем) U₀. С одной стороны, использование ее в качестве граничного условия для электрической составляющей ДДМТ позволяет в каждый момент времени оценить параметры источников и приемников тепла для уравнения (1), рассчитать температурное поле внутри структуры и получить значение длительности импульса, необходимое для достижения заданной максимальной температуры. С другой стороны, значение напряжения U₀ и полученная длительность импульса t_p дают "внешние" энергомощностные характеристики.

В зависимости от соотношения указанных слагаемых будет наблюдаться разное поведение энергомощностных характеристик внешнего импульсного воздействия. Если до воздействия в идеальном случае существует полное согласование (равенство) сопротивлений антенны или генератора и диодной структуры, то при воздействии импульса изменение сопротивления диодной структуры будет влиять на соотношение слагаемых уравнения (4). Как показано в [14, 18, 19], сопротивление диодной структуры при этом будет уменьшаться, и бóльшая часть падающей мощности будет приходиться именно на структуру. В результате характер поведения P_inc будет близок к P_av. Если же изначально сопротивление R значительно меньше сопротивления диодной структуры (например, случайная антенна в виде низкоомных межсоединений на платах аппаратуры), то бóльшая часть падающей мощности будет приходиться на R, а характер поведения P_inc будет соответствовать P_R. Рассмотрим оба этих случая.

 

Результаты моделирования

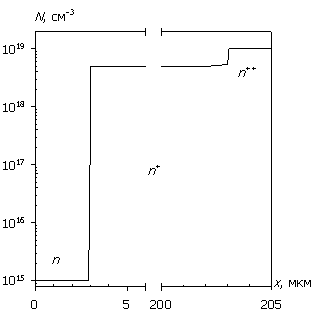
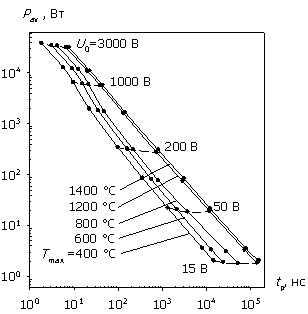
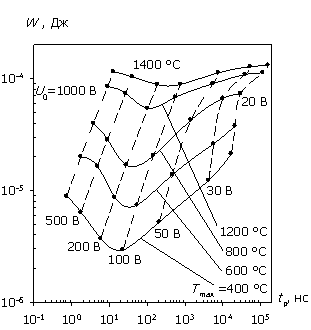
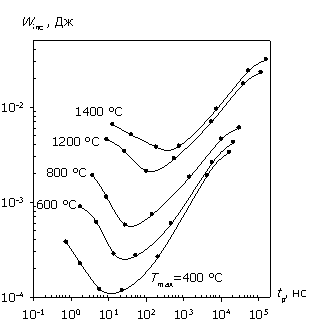
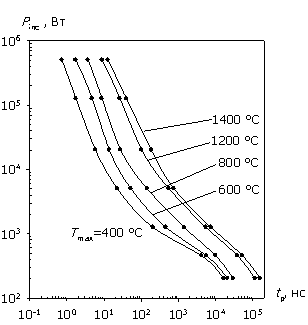
На рис. 2а, 2б приведены зависимости W и P_av от длительности СВЧ-импульса с несущей частотой f = 1 ГГц для биполярной структуры и структуры с барьером Шоттки, полученные согласно уравнениям (2) и (3) из результатов численного моделирования их внутренних электротепловых характеристик вплоть до температуры плавления кремния (1400 °С). Штриховыми линиями показаны одинаковые амплитуды воздействующего сигнала.

Графики на рис. 2 содержат ранее известные из теоретических расчетов и экспериментальных данных характерные участки поведения энергомощностных характеристик при различных длительностях импульсного воздействия: в определенных диапазонах t_p они близки к известным зависимостям Вунша–Белла [9] и адиабатической [2, 10]. Кроме того, в области сверхкоротких импульсов (t_p < 10…50 нс) при U₀ > 200 В наблюдается экспериментально выявленный в [20] участок (назовем его "генерационный"), характеризующийся ростом энергии с дальнейшим ее насыщением. Причиной возникновения этого участка является  рассматриваемый в ДДМТ приемник тепла, связанный с генерационными процессами, наиболее существенными при больших значениях амплитуды воздействующего сигнала, в то время как в тепловых моделях априорно предполагается наличие только источников тепла, приводящих непосредственно к разогреву структуры [11, 12].

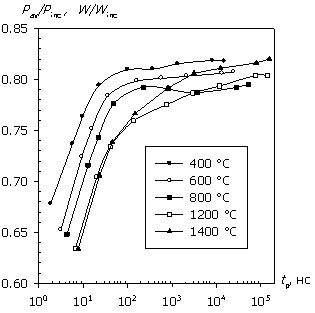
На рис. 3а, 3б показаны рассчитанные в условиях полного согласования (R = 250 Ом) соотношения рассеиваемой мощности (энергии) и падающей мощности (энергии) для исследуемых структур. Из представленных характеристик видно, что при t_p = 10⁰…10⁵ нс рассеиваемые мощность P_av и энергия W составляют 60…80 % от падающей мощности P_inc (энергии W_inc) для биполярной структуры и 50…90 % для структуры с барьером Шоттки в зависимости от максимальной температуры разогрева T_max и длительности однократного СВЧ-импульса.

Характер поведения кривых отношения мощностей (энергий) на рис. 3 противоположен поведению кривых мощностей (энергий) на рис. 2: максимальным значениям зависимости W/W_inc(t_p) соответствует минимум зависимости W(t_p), а замедление роста рассеиваемой энергии в областях очень коротких импульсов (менее 10 нс) и длинных импульсов (более 10⁴ нс) приводит к резкому изменению соотношения W/W_inc(t_p).

Так как в биполярной структуре неосновные носители играют определяющую роль во всех механизмах зарядопереноса, а следовательно, и теплопереноса (через тепловую обратную связь), то рекомбинационные процессы в них более существенны, чем в униполярных структурах с барьером Шоттки. Это приводит к выравниванию распределения мощности и температуры по всей глубине биполярной структуры. Из зависимости W(t_p) видно, что рост энергии на "генерационном" участке в области коротких импульсов у биполярных структур (рис. 2а) менее выражен, чем у структур с барьером Шоттки (рис. 2б) из-за быстро нарастающей компенсации темпа генерации (приемника тепла) темпом рекомбинации (источником тепла). Этим же объясняется и более выраженное насыщение W(t_p) при дальнейшем уменьшении времени импульсного воздействия. В результате размытость максимума характеристики W/W_inc(t_p) для биполярной структуры больше, чем для структуры с барьером Шоттки (см. рис. 3).

 

     

(а)

    

(б)

Рис. 2. Зависимости W(t_p) и P_av(t_p);
а – биполярная структура; б – структура с барьером Шоттки.

 

  

(а)                                                            (б)

 

Рис. 3. Соотношения рассеиваемой и падающей мощности (энергии);
СВЧ-импульс; полное согласование; а – биполярная структура,
б – структура с барьером Шоттки.

 

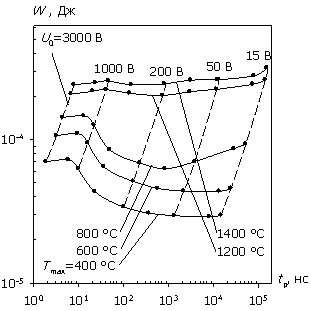
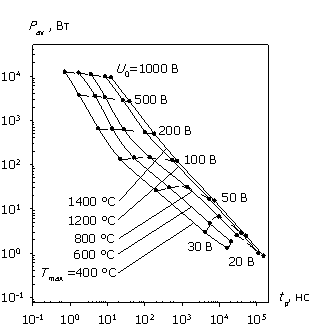
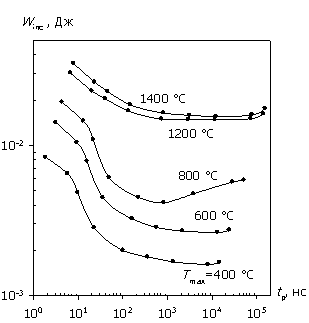
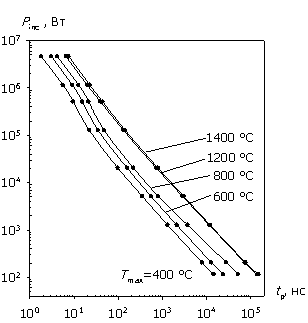
На рис. 4а, 4б показаны рассчитанные для диодных структур в условиях отсутствия согласования (R = 1 Ом) падающая мощность и энергия в зависимости от длительности СВЧ-импульса. Сравнение энергомощностных характеристик (рис. 2 и рис. 4) показывает, что в этом случае P_inc и W_inc больше P_av и W  почти на два порядка, и в отличие от полного согласования в данном случае соотношения мощностей составляют доли процента. Но при этом усиливается искажение характеристик P_inc и W_inc в силу уравнений (4), (5) и формы соотношений W/W_inc(t_p) и P/P_inc(t_p) на рис. 3. Сравнение рис. 2 и рис. 4 показывает, что зависимость W_inc(t_p) растет значительно быстрее W(t_p) для биполярной структуры при U₀ > 200 В и для структуры с барьером Шоттки при U₀ < 50 В. Иными словами, использование экспериментально наблюдаемой зависимости W_inc(t_p) (или Р_inc(t_p)) может давать существенную погрешность в оценке температуры теплового поражения, которая тем больше, чем больше степень рассогласования.

Очевидно, что отмеченные различия в энергомощностных характеристиках при воздействии СВЧ-импульса будут проявляться и для других форм импульсов. На рис. 5а, 5б приведены результаты расчетов падающей и рассеиваемой мощности (энергии) для прямоугольных импульсов различной полярности при R = 1 Ом в сравнении с СВЧ-импульсом. Обозначено: П⁺ – прямая полярность, П^- – обратная.

Сравнительный анализ представленных на рис. 5 графиков показывает следующее. Наибольшее различие в характере поведения энергомощностных характеристик диодных структур наблюдается при воздействии П^--импульса.

      

(а)

      

(б)

Рис. 4. Зависимости W_inc(t_p) и P_inc(t_p); отсутствие согласования; СВЧ-импульс;

а – биполярная структура; б – структура с барьером Шоттки.

 

    

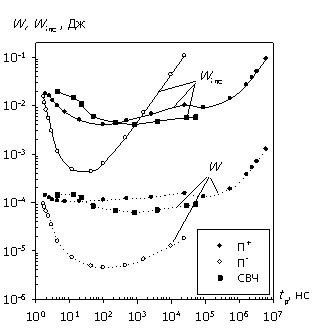
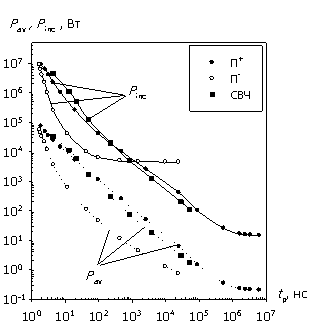
(а)

   

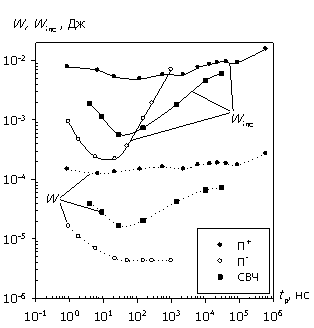
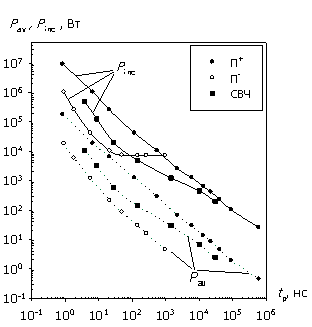
(б)

 

Рис. 5. Зависимости W(t_p), W_inc(t_p), P_av(t_p) и P_inc(t_p) для СВЧ и прямоугольных импульсов; отсутствие согласования; T_max = 800 ºС; а – биполярная структура;
б – структура с барьером Шоттки.

 

В этом случае обе структуры могут пропустить значительный ток, приводящий к тепловому разогреву до определенной температуры, только в состоянии лавинного пробоя. Следовательно, уровень воздействующего напряжения при увеличении времени импульса асимптотически стремится сверху к пробивному напряжению. В итоге, "внутренние" характеристики показывают насыщение энергии W, так как объем, затронутый лавинной генерацией, практически постоянен. Это насыщение особенно выражено для структур с барьером Шоттки, где рекомбинационные процессы менее значимы. Средняя за время импульса мощность P_av при этом падает. Противоположно этому "внешние" характеристики в силу уравнения (4) дают насыщение мощности P_inc (требуется поддержка определенного уровня напряжения U₀ при любой длительности импульса), но тогда из уравнения (5) получаем асимптотически бесконечный рост энергии W_inc с увеличением t_p.

Наименьшее различие в характеристиках наблюдается при воздействии П⁺-импульса, дающего наиболее равномерное распределение рассеиваемой мощности по всей длине структуры. Следует также предполагать наличие указанных для П^--импульса участков насыщения W и P_inc при t_p > 10⁷ нс, когда уровень напряжения приближается к стационарному значению (точка вольт-амперной характеристики), соответствующему заданной температуре разогрева.

Характеристики воздействия СВЧ-импульса находятся, в общем случае, между характеристиками прямоугольных импульсов. Отклонения от этой тенденции связаны с генерационно-рекомбинационными процессами, изменением объема локализации и перераспределением внутри структуры энергии, идущей на тепловой разогрев согласно уравнению (1). Как следует из рис. 5 для биполярной структуры воздействие СВЧ-импульса ближе к воздействию
П⁺-импульса при t_p = 1…10⁵ нс. Для структуры с барьером Шоттки воздействие СВЧ-импульса ближе к воздействию П⁺-импульса при t_p = 10²…10⁵ нс и к воздействию П^--импульса при t_p = 1…10² нс.

 

Заключение

Результаты моделирования демонстрируют, что оценки мощности и энергии теплового разогрева импульсным ЭМИ по "внешнему" и "внутреннему" критериям отличаются как по величине, так и по характеру поведения, и существенно зависят от степени согласования сопротивлений антенны (генератора, схемы измерения) и диодной структуры. Наибольшее расхождение в оценках по указанным критериям свойственно прямоугольному импульсу обратной полярности при стремлении напряжения воздействующего сигнала к пробивному напряжению диодной структуры.

На основании полученных результатов моделирования можно утверждать, что согласованные антенные тракты приемо-передающей радиоэлектронной аппаратуры, содержащие полупроводниковые детекторные и смесительные диоды, наиболее подвержены тепловому поражению мощным СВЧ ЭМИ.

 

Литература

1.            Сорокин Л.Н., Усыченко В.Г., Щерстюк А.В. Выгорание полупроводниковых приборов под воздействием сверхвысокочастотных импульсов и электрических видеоимпульсов // Радиотехника и электроника. – 2010. – Т. 55. – № 5. – С. 631-638.

2.            Dwyer V.M., Franklin A.J., Campbell D.S. Thermal failure in semiconductor devices // Solid-State Electronics. – 1990. – V.33. – N 5. – P. 553-560.

3.            Anand Y., Moroney W.J. Microwave mixer and detector diodes // Proceedings of the IEEE. – 1971. – V. 59. – N 8. – P. 1182-1190

4.            Ahmad K. RF burnout in X-band Schottky mixers // Journal of Applied Physic. – 1972. – V. 43. – N 11. – P. 4826-4827.

5.            Guccione S.A. Pulse burnout of microwave mixer diodes // IEEE Transaction on Reliability. – 1973. – V. R-22. – N. 4. – P. 196-207.

6.            Whalen J.J. The RF pulse susceptibility of UHF transistors // IEEE Transaction on Electromagnetic Compatibility. – 1975. – V. EMC-17. – N 4. – P. 220-225.

7.            Diaz C., Kang S., Duvvury Ch. Simulation of electrical overstress thermal failures in integrated circuits // IEEE Transaction on Electron Devices. – 1994. – V. ED-41. – N. 3. – P. 359-366.

8.            Anand Y. X-band high burnout resistance Schottky-barrier diodes // IEEE Transaction on Electron Devices. – 1977. – V. ED-24. – N. 12. – P. 1330-1336.

9.            Wunsh D.C., Bell R.R. Determination of threshold failure levels of semiconductor diodes and transistors due to pulse voltage // IEEE Transaction on Nuclear Science. – 1968. – V. NS-15. – N 6. – P. 244-259.

10.       Taska D.M. Pulse power failure modes in semiconductors // IEEE Transaction on Nuclear Science. – 1970. – V. NS-17. – N 7. – P. 364-372.

11.       Мещеряков С.А. Моделирование физических процессов в полупроводниковых структурах при воздействии мощного СВЧ-импульса. Структуры с барьером Шоттки [Электронный ресурс] // Журнал радиоэлектроники: электронный журнал. – 2013. – № 11. – Режим доступа: http://jre.cplire.ru/jre/nov13/2/text.pdf.

12.       Мещеряков С.А. Моделирование физических процессов в полупроводниковых структурах при воздействии мощного СВЧ-импульса. Биполярные структуры [Электронный ресурс] // Журнал радиоэлектроники: электронный журнал. – 2013. – № 12. – Режим доступа: http://jre.cplire.ru/jre/dec13/6/text.pdf.

13.       Мещеряков С.А. Моделирование теплового поражения диодных полупроводниковых структур полиимпульсным сверхвысокочастотным радиоизлучением [Электронный ресурс] // Журнал радиоэлектроники: электронный журнал. – 2013. – № 7. – Режим доступа: http://jre.cplire.ru/jre/jul13/4/text.pdf.

14.       Бердышев А.В., Мещеряков С.А. Численное моделирование физических процессов в кремниевых полупроводниковых p – n-переходных структурах при воздействии электромагнитного излучения сверхкоротких импульсов // Радиотехника и электроника. – 2013. – Т. 58. – № 7. – С. 726-734.

15.       Мещеряков С.А., Бердышев А.В. Электротепловая модель воздействия электромагнитного излучения на полупроводниковые структуры // Радиотехника и электроника. – 2013. – Т. 58. – № 11. – С. 1127-1135.

16.       NSM Archive – Physical Properties of Semiconductors [Электронный ресурс]. Режим доступа: http://www.ioffe.rssi.ru\SVA\NSM\Semicond\index.html.

17.       Диоды: Справочник / О.П. Григорьев и др. М.: Радио и связь, 1990.

18.       Brown W.D. Semiconductor device degradation by high amplitude current pulses // IEEE Transaction on Nuclear Science. – 1972. – V. NS-19. – N 2. –
P. 68-75.

19.       Prokopyev A.I., Mesheryakov S.A. Static characteristics of high-barrier Schottky diode under high level injection // Solid-State Electronics. – 1999. – V. 43. – N 9. – P. 1747-1753.

20.       Юшков Ю.Г., Чумерин П.Ю., Артеменко С.Н. и др.  Экспериментальное исследование воздействия сверхвысокочастотных импульсов на работу персонального компьютера // Радиотехника и электроника. – 2001. – Т. 46. – № 8. – С. 1020-1024.