УДК 621.391
Когерентная передача цифровой информации с двоичной модуляцией хаотического импульса
Т. И. Мохсени 1, А. М. Кикот 2
1 Институт радиотехники и электроники им. В.А. Котельникова РАН
2 Московский физико-технический институт
Статья получена 8 июня 2015 г.
Аннотация. В работе рассмотрена возможность применения концепции программно-конфигурируемого радио для построения беспроводной системы связи на основе хаотических сигналов, обеспечивающей когерентный прием. Когерентность обеспечивается за счет использования эталонного фрагмента хаотического сигнала, хранимого в памяти приемника и передатчика в цифровом виде. Проведено моделирование на основе рассмотренного подхода. По результатам моделирования поставлены физические эксперименты по реализации радиосистемы когерентного приема/передачи информации с помощью хаотических импульсов.
Ключевые слова: программно-конфигурируемое радио, хаотическая динамика, хаотический сигнал, когерентный прием.
Abstract. The paper considers the possibility of applying the concept of software defined radio for building wireless communication system based on chaotic signals and providing coherent detection. Coherence is achieved by using a reference fragment of chaotic signal stored in the memory of transmitter and receiver in digital form. Simulation model based on the considered approach was built. As a result of simulation experimental testbed providing transmission and coherent detection of information signal using chaotic pulses was set up.
Key words: software defined radio, chaotic dynamics, chaotic signal, coherent detection.
Введение
Хаотические сигналы с начала 90-х годов привлекают внимание исследователей в области передачи информации, в том числе и для беспроводных систем. В первой половине 90-х был опубликован ряд работ, в которых были представлены схемы для передачи данных с помощью динамического хаоса, такие как: хаотическая маскировка [1], переключение хаотических режимов [2], нелинейное подмешивание [3, 4]. Тем самым была показана принципиальная возможность использования явления динамического хаоса в коммуникационных системах в качестве носителей информации. На этом этапе, большинство предложенных схем по передаче информации с использованием хаотических сигналов основывалось на явлении хаотической синхронизации [5, 6]. Однако, к середине 90-х годов проведенный анализ описанных схем с использованием динамического хаоса показал, что построение радиосистемы, использующей хаотическую динамику в принципе возможно, но сопряжено с рядом проблем, главной из которых является крайне низкая устойчивость явления хаотической синхронизации возмущающим факторам: фильтрующим свойствам канала, несовпадению параметров хаотических модулей приемника и передатчика, помехам в канале [7]. Был проведен ряд исследований, посвященных анализу причин этих неустойчивостей, а также разработке систем связи, построенных с использованием динамического хаоса, но без использования хаотической синхронизации [8].
Исследования по построению схем, использующих динамический хаос, но не использующих хаотическую синхронизацию привели к созданию устойчивых к возмущениям схем передачи: дифференциальное переключение хаотических режимов (Differential chaotic shift keying) [9] и прямохаотическая система связи (ПХСС) [10]. Первая из них использовала метод относительной антиподальной модуляции, вторая, разработанная в Институте радиотехники и электроники им. В.А. Котельникова Российской академии наук (ИРЭ им. В.А. Котельникова РАН), основывалась на энергетическом приеме хаотических радиоимпульсов или другими словами использовала детектор огибающей.
Вместе с тем, вопрос о когерентном приеме хаотических сигналов и даже использовании хаотической синхронизации остается открытым. Так, например в [11] проведены сравнительные исследования когерентного и некогерентного приема потока информации, передаваемого при помощи хаотических радиоимпульсов. Согласно этим исследованиям отношение средней энергии хаотического радиоимпульса Eб к спектральной плотности гауссовского шума N0 при вероятности ошибки P=10-3 в случае когерентного приема может быть на 2,5-4,5 дБ меньше чем в случае некогерентного приема в интервале значений базы сигнала 10<B<50, и эта разница между отношениями Eб/N0 растет с увеличением базы.
Одной из главных проблем при создании схем связи с использованием динамического хаоса является практическая невозможность построения идентичных хаотических систем на передающей и принимающей стороне. Такие ограничения делают сложной передачу данных даже в условиях хорошего или идеального канала связи.
Вопрос об «идентичности» хаотического сигнала на передатчике и приемнике может быть решен в случае цифровой реализации устройств на предающей и принимающей стороне, т.е. фактически при программной реализации хаотического передатчика и хаотического приемника. В этом случае, при хорошем канале связи, можно получить хорошее качество передачи. Например, такие эксперименты по цифровой реализации проводились в ИРЭ им. В.А. Котельникова РАН со схемой нелинейного подмешивания с использованием цифрового микроконтроллера и продемонстрировали улучшение качества предаваемого акустического сигнала на 10-15дБ по сравнению с аналоговым подходом [12].
Однако использование цифровой реализации хаотических систем на передатчике и приемнике не решает проблему качества канала, а следовательно характеристики систем, базирующихся на хаотической синхронизации, в целом катастрофически ухудшаются, если этот канал слегка зашумлен или в нем имеются другие искажения. Поэтому целесообразнее рассмотрение когерентного приема, не использующего свойства хаотической синхронизации. В данной работе предлагается использование в передатчике и приемнике одинаковых копий несущего хаотического сигнала и синхронизация этих копий во времени с помощью внешних средств. В этом случае введение информации на передающей стороне может осуществлять стандартными методами модуляции, применяемыми в системах связи, использующих когерентный прием, т.е. например, модуляция исходного потока импульсами фиксированной длины полярности «+1» и «-1», что является аналогом метода модуляции BPSK.
Такая возможность исследовалась в работе [13], где было показано, что подобные системы по своим характеристикам близки системам, использующим CDMA, и могут, например, работать в условиях, когда уровень сигнала в канале значительно ниже уровня шума, а так же в условиях других сильных искажений.
Проблема создания подобных систем связи заключается в том, что они требуют очень больших объемов высокоскоростных вычислений. Поэтому речь может идти либо о достаточно узкополосных радиосигналах, либо «насчитывать» копии данных сигналов с последующей записью и выборкой из памяти.
В данной работе предполагается использовать заранее рассчитанные фрагменты, записываемые в память приемника и передатчика, так как время извлечения фрагментов из памяти значительно меньше, чем время их расчета. Для того, чтобы упростить задачу будет использована не длинная хаотическая последовательность, а достаточно короткие фрагменты хаотических сигналов, которые будут использоваться в качестве системы ортогональных сигналов. Для экспериментальной реализации рассматриваемого подхода в работе используется аппаратура National Instruments.
1. Когерентная система цифровой передачи с одной базовой функцией в виде хаотического радиоимпульса
Рассмотрим систему передачи цифровой информации по полосовому каналу (рис. 1).
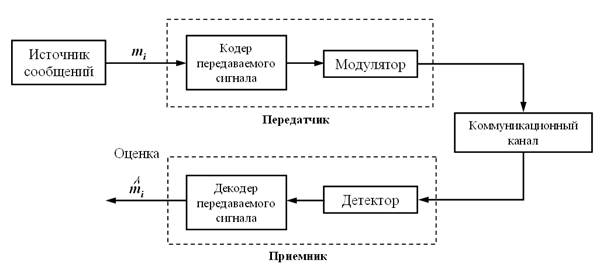
Рис.1. Модель полосовой передающей системы
Она состоит из: источника сообщений, который порождает один символ каждые T секунд, где символы принадлежат алфавиту из M символов и обозначается через m1, m2, mM; кодера передаваемого сигнала, который преобразует выходные сигналы источника mi в соответствующие сигнальные векторы s , состоящие из N реальных физических элементов. Число N меньше или равно M. Имея si на входе, модулятор производит определенный сигнал si(t) длительностью T секунд в качестве представления символа mi, генерируемого источником. Сигналы si(t) имеют ограниченную энергию:
![]() i = 1,2…M (1)
i = 1,2…M (1)
В системе передачи с одной базовой функцией в виде фрагмента хаотического сигнала будем использовать пару сигналов s1(t) и s2(t) для представления символов «1» и «0» соответственно. Пусть φ1(t) – базовая функция – фрагмент хаотического сигнала. Тогда s1(t) и s2(t) определяются в виде:
![]()
![]() ,
(2)
,
(2)
где 0 ≤ t ≤ Tб и Eб – энергия сигнала, приходящаяся на бит передаваемой информации. Когерентная система передачи с одной базовой функцией в виде фрагмента хаотического сигнала характеризуется одномерным пространством сигналов (т.е. N=1) с созвездием сигналов, состоящим из двух точек-сообщений (т.е. M=2), как показано на рис. 2.
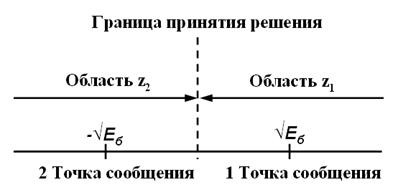
Рис. 2. Диаграмма пространства сигналов для когерентной системы с двоичной фазовой модуляцией
Координаты точек-сообщений:
![]()
![]() .
(3)
.
(3)
Правило принятия решения заключается в выборе принадлежности принятого сигнала к областям z1 или z2.
Для генерации сигнала с
антиподальной модуляцией фрагмента хаотического сигнала нужно представить
входную двоичную последовательность импульсов, состоящую из «1» и «0» в виде
сигнала с постоянными уровнями амплитуды ![]() и
и ![]() соответственно. Это кодирование
передаваемого сигнала осуществляется с помощью кодера уровней «без возврата к
нулю» (nonreturn-to-zero - NRZ). В результате двоичная волна
(сигнал в полярной форме) и хаотический носитель φ1(t) перемножается в модуляторе (рис. 3). На входе
модулятора получается требуемый сигнал с антиподальной модуляцией фрагмента
хаотических колебаний.
соответственно. Это кодирование
передаваемого сигнала осуществляется с помощью кодера уровней «без возврата к
нулю» (nonreturn-to-zero - NRZ). В результате двоичная волна
(сигнал в полярной форме) и хаотический носитель φ1(t) перемножается в модуляторе (рис. 3). На входе
модулятора получается требуемый сигнал с антиподальной модуляцией фрагмента
хаотических колебаний.
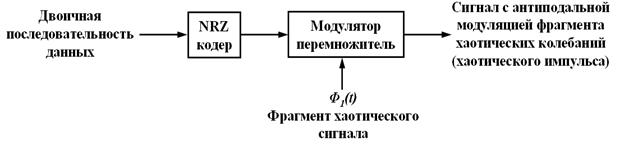
Рис. 3. Блок-схема передатчика с двоичной модуляцией хаотического сигнала
Для детектирования исходной двоичной последовательности «1» и «0» зашумленный сигнал x(t) = s(t) + η(t) используем коррелятор. На второй вход коррелятора подается локально сгенерированный опорный сигнал φ1(t) (рис. 4). Выходной сигнал коррелятор x1 сравнивается с нулевым порогом. Если x1 > 0, то приемник решает, что поступил символ «1». В противном случае принимается решение, что поступил символ «0».
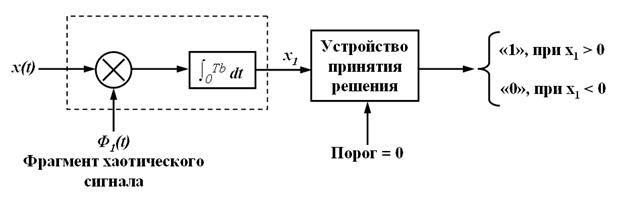
Рис. 4. Блок-схема приемника с двоичной модуляцией хаотического сигнала
2. Выбор эталонного фрагмента хаотического сигнала
Для получения цифрового фрагмента эталонного хаотического сигнала фиксированной длины в работе использовалась среда моделирования Matlab. В качестве источника хаоса использовалась модель прецизионного генератора хаоса с 1,5 степенями свободы [14].
Данный генератор принадлежит к классу хаотических кольцевых автоколебательных систем, в которых составляющие генератор элементы последовательно соединяют в схему, образующую единое кольцо обратной связи. Блок схема генератора изображена на рис. 1а Генератор состоит из нелинейного элемента F(z) (подсистема 1 (рис. 5б)) с амплитудным преобразованием входного сигнала z, R1C1-фильтра нижних частот (подсистема 2 (рис. 5б)), R2L2C2-фильтра нижних частот (подсистема 3 (рис. 5б)) и является автоколебательной системой с 1,5 степенями свободы. Буферные каскады реализованы на операционных усилителях.
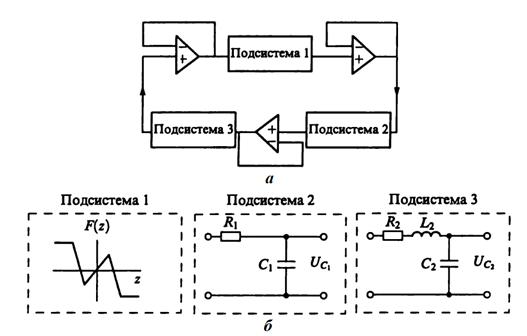
Рис. 5. Кольцевой генератор хаоса с 1,5 степенями свободы: а – блок-схема генератора; б – структура подсистем генератора
В качестве нелинейного элемента в генераторе используется элемент с кусочно-линейной пятисегментной характеристикой:
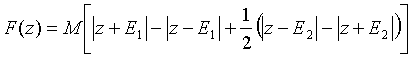 , (5)
, (5)
где Е1, E2 – константы, М – коэффициент усиления. Конкретный выбор E1, E2 и M однозначно определяет характеристику (5).
Динамические режимы генератора описываются с помощью дифференциальных уравнений, получаемых из законов Кирхгофа для подсистем-четырехполюсников (рис. 5б).
Обозначая напряжения на конденсаторах C1 и C2 через UC1 и UC2 соответственно, рассмотрим каждую из трех подсистем.
Подсистема 1 представляет собой четырехполюсник с нелинейной функцией преобразования амплитуды входного сигнала F(z) (5). Входным сигналом для нее является выходной сигнал подсистемы 3, т. е. напряжение UC2. Таким образом, выходным сигналом подсистемы 1 является напряжение F(UC2).
Подсистема 2 представляет собой фильтр нижних частот первого порядка, на вход которого подается напряжение F(UC2), а выходным сигналом является UC1. В соответствие со вторым законом Кирхгофа, и с учетом большого входного сопротивления буферного каскада, подсоединенного к выходу подсистемы, зависимость между напряжениями описывается уравнением
![]() (6)
(6)
Подсистема 3 является фильтром нижних частот второго порядка с выходным напряжением UC1 и выходным UC2. По аналогии с подсистемой 2, применение закона Кирхгофа дает следующее уравнение:
![]() (7)
(7)
Если обозначить UC1 = x, UC2 = z, C1R1 = T, R2/L2 = α, 1(L2C2) = ω2 и ввести новую переменную y = (dUC2/dt) – R2UC2/L2, то из (6) и (7) следует система дифференциальных уравнений, описывающих динамические режимы генератора:
![]() ,
, ![]() ,
, ![]() .
(8)
.
(8)
Система (8) позволяет использовать стандартные методы решения дифференциальных уравнений (например, метод Рунге-Кутта) для анализа динамических режимов генератора. Результатом решения системы являются зависимости x(t) и z(t). Изменяя параметры системы (M, T, ω, α, E1, E2) и анализируя реализации x(t) и z(t) можно получить различные режимы генератора.
Согласно [14] при значении параметров M=5, T=3, ω=1, α=0,22, E1=0,5, E2=2 генератор находится в хаотическом режиме. Результаты численного моделирования (8) представлены на рисунке 6.
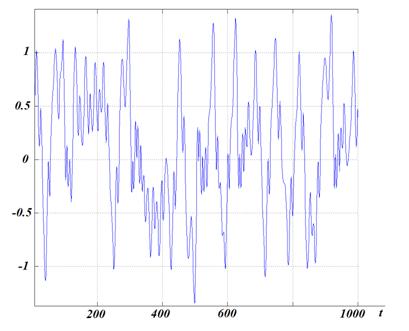
Рис. 6а.
Фрагмент временной реализации хаотического режима модели кольцевого
автогенератора с 1,5 степенями свободы
(значение параметров системы: M=5, T=3,
ω=1, α=0,22, E1=0,5, E2=2).
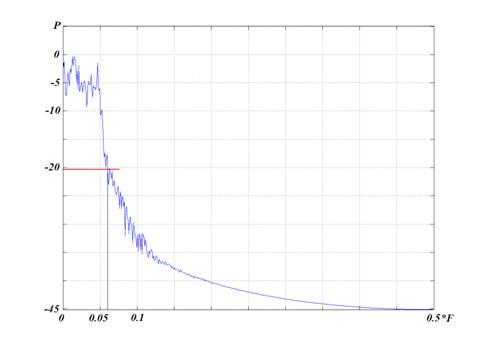
Рис. 6б.
Спектр мощности хаотического режима модели кольцевого автогенератора с 1,5
степенями свободы
(значение параметров системы: M=5, T=3, ω=1,
α=0,22, E1=0,5, E2=2).
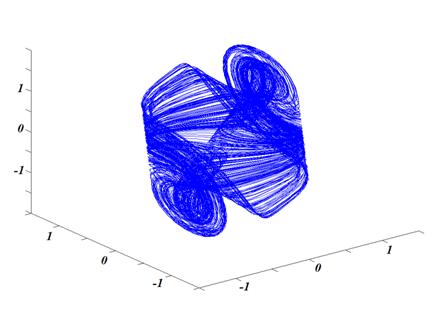
Рис. 6в. Фазовый портрет хаотического
режима модели кольцевого автогенератора с 1,5 степенями свободы
(значение
параметров системы: M=5, T=3, ω=1, α=0,22, E1=0,5, E2=2).
Фрагмент выбирается достаточно длинным (>20 квазипериодов) для расчета полосы спектра смоделированного хаотического сигнала. В работе используется частота дискретизации Fд = 80 МГц. Спектральная полоса получаемого в результате моделирования фрагмента хаотического сигнала находится в пределах от 0 до 0,06*Fд (рис. 6б). На рис. 6в изображен фазовый портрет рассчитанного хаотического режима кольцевого автогенератора с 1,5 степенями свободы. Длительность эталонного фрагмента динамического хаоса составляла Tб = 1000/Fд = 12,5 мкс.
3. Программно-определяемая радиосистема
Практическая реализация предлагаемой схемы будет осуществлена на основе концепции программно-конфигурируемого радио (ПКР).
Согласно концепции технологии ПКР [15,16] практически весь объем работ по обработке сигнала перекладывается на программное обеспечение. То есть программно-конфигурируемая система – это радиокоммуникационный комплекс, в котором основные аппаратные компоненты (фильтры, усилители, модуляторы, демодуляторы) реализованы программным способом. Так как аппаратные компоненты приемопередающих систем, основанных на концепции ПКР, полностью настраиваются программными средствами, появляется возможность модификации таких системы без каких либо значительных изменений в аппаратной конфигурации. При использовании систем ПКР программное обеспечение, которое выполняет практически весь объем работ, запускается на цифровых сигнальных процессорах или на программируемых логических интегральных схемах (ПЛИС). Цель такого подхода – создавать системы, которые могут принимать и передавать практически любые радиосигналы с любыми типами аналоговой и цифровой модуляции.
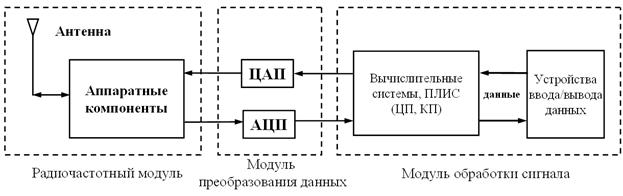
Рис. 7. Общая схема программируемого радио
В классическом представлении (рис. 7) система ПКР собой центральный процессор (ЦП), оснащенный приемным и передающим блоками. Роль ЦП заключается в выводе/вводе данных в систему, а также получении управляющих команд и их последующей трансляции соответствующим компонентам.
В [17] указывается, что передающий блок имеет коммуникационный процессор (КП), основной задачей которого является упаковка битов передаваемых данных в символы модуляции и генерация на их основе модулирующего сигнала определенной системы связи, который поступает на цифро-аналоговый преобразователь (ЦАП) и далее на аналоговый радиоинтерфейс.
Приемный блок содержит аппаратную аналоговую часть, аналого-цифровой преобразователь (АЦП), КП, осуществляющий демодуляцию сигнала и преобразование демодулированных символов системы связи в биты данных.
Программно-определяемые радиосистемы могут быть реализованы как на вычислительных средствах общего назначения, так и на ПЛИС, осуществляющих обработку сигнала в реальном времени. При этом за пределы ПЛИС выносятся радиоинтерфейсы, а также АЦП и ЦАП. Применение ПЛИС не приводит к снижению гибкости системы, поскольку ПЛИС могут быть в любой момент полностью или частично перепрограммированы.
Использование в технологии ПКР цифровых методов формирования и обработки сигналов, как базового принципа, позволяет эффективно использовать для достижения цели работы.
4. Моделирование программно-определяемой хаотической приемо-передающей системы в пакете LabView
Первым этапом является создание модели исходной приемо-передающей системы. Целью моделирования является отработка алгоритмов работы системы для последующего физического эксперимента.
Модель была создана в программном пакете LabView. Это сделано из расчета, что в дальнейшем при проведении эксперимента с помощью приемо-передающего устройства, большая часть обработки данных, например считывание реализации хаотического сигнала из памяти передатчика и приемника, будет производиться с помощью этого программного обеспечения.
Блок-схема модели представлена на рис. 8.
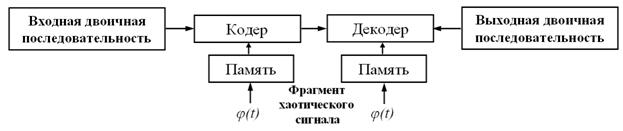
Рис. 8. Принципиальная блок-схема модели.
На схеме изображено кодирование входной двоичной последовательности с использованием фрагмента хаотического сигнала, взятого из памяти. Полученный сигнал передавался в декодер. После происходило декодирование при помощи такого же фрагмента хаотического сигнала. Результатом являлась выходная двоичная последовательность.
Рассмотрим подробнее кодер и декодер. Заранее рассчитанный фрагмент хаотического сигнала записывался в память передатчика и приемника.
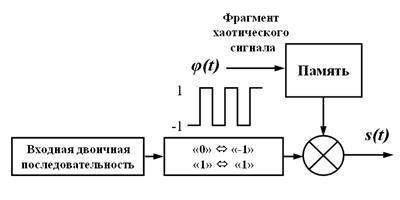
Рис. 9. Схема формирования кодированного сигнала.
При кодировании данных, на вход кодера, изображенного на рис. 9, подавалась двоичная последовательность, состоящая из нулей и единиц. Данная последовательность преобразовывалась в двухуровневый сигнал с уровнями «-1» и «1», где уровень «-1» соответствовал символу «0», а уровень «1» - символу «-1». Длительность одного бита полученного сигнала равнялась длительности фрагмента хаотического сигнала φ(t), извлеченного из памяти. Далее двухуровневый и хаотический сигналы перемножались с учетом синхронизации, в результате чего на выходе кодера получался модулированный хаотический сигнал s(t).
Сформированный таким образом сигнал s(t) передавался на декодер приемника по идеальному каналу. В модели считалось, что кодер (передающая сторона) и декодер (приемная сторона) синхронизированы во времени между собой.
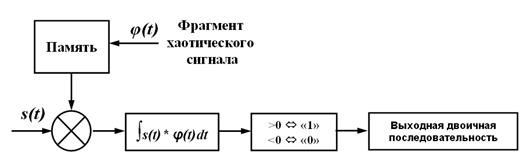
Рис. 10. Схема декодирования принятого сигнала.
При декодировании (рис. 10) принятый сигнал s(t) делился на отрезки длительности, равные длительности эталонного фрагмента хаотического сигнала. Эти отрезки хаотического сигнала обрабатывались с использованием записанного в память приемника фрагментом хаотического сигнала следующим образом: отрезки принятого сигнала перемножалась с фрагментом хаотического сигнала, извлекаемого из памяти приемника, затем полученное произведение интегрировалось по всей длине фрагмента опорного хаотического сигнала. Результат интегрирования сравнивался с нулем. Если он был больше нуля, то делался вывод, что принята единица, если меньше – то нуль. В соответствии с полученными в результате обработки значениями двоичных символов на выходе декодера формировалась двоичная информационная последовательность, состоящая из нулей и единиц.
Использование программного пакета LabView при моделировании позволило эмулировать все описанные аналоговые процессы в цифровом виде. Фактически описанная выше схема в цифровом виде является цифровой частью построенной системы связи, описанной в следующей главе. Построенная модель послужила основой для разработки цифровой части приемника и передатчика рассматриваемой в работе системы когерентного приема и передачи информации на основе хаотических импульсов.
Схема моделирования в среде LabView представлена на рис. 11. Результаты моделирования представлены на рис. 12.
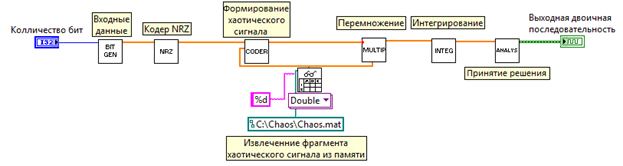
Рис. 11 Схема модели в среде LabView.
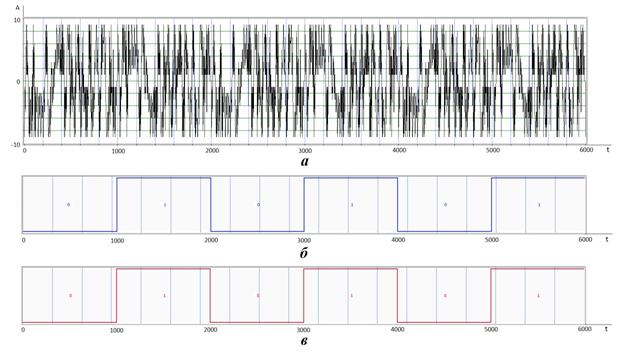
Рис. 12. Результаты моделирования.
На рис. 12а изображен сформированный в соответствии с входной двоичной информационной последовательностью хаотический сигнал. На рис. 12б,в изображены соответственно построенные на основе входной и выходной двоичных информационных последовательностей двухуровневые сигналы. Как видно из рис. 12б,в в результате работы смоделированной системы связи двухуровневые сигналы на передатчике и приемнике, содержащие соответственно входную и выходную двоичные информационные последовательности, совпали.
В процессе проведенного моделирования на основе двоичной информационной последовательности сформирован, передан и корректно обработан сигнал, состоящий из фрагментов хаотических сигналов, предварительно сгенерированных и записанных в память передатчика и приемника. Это позволило перейти к постановке и проведению физических экспериментов.
5. Эксперимент
По результатам моделирования программно-определяемой приемо-передающей хаотической системы связи, обеспечивающей когерентный прием, был поставлен физический эксперимент. Эксперимент проводился в режиме «точка-точка». Приемник и передатчик располагались на расстоянии порядка 1 м друг от друга. В качестве передающего и приемного устройств были созданы идентичные макеты системы ПКР. Макеты приемо-передающей системы были собраны на основе модульного оборудования PXI [16] от компании National Instruments. Системы PXI представляют собой шасси, состоящие из объединенных в общую панель и соединенных шиной передачи данных PXI-слотов, предназначенных для системного контроллера и периферийных модулей. Все используемые модули располагались в PXI-слотах шасси модели NI PXI 1055, с которое обеспечивало связь между модулями макета ПКР.

Рис. 13. Макет системы ПКР, собранный
из модулей компании National
Instruments,
использовавшийся в эксперименте в
качестве приемника/передатчика
Формирование модулированного цифрового хаотического сигнала осуществлялось в baseband диапазоне с помощью встраиваемого системного контроллера NI 8133 с операционной системой Windows 7. Управление контроллером осуществлялось через среду программирования LabView.
Заранее рассчитанный эталонный фрагмент реализации хаотического сигнала записывался в память приемника и передатчика. На вход передатчика поступала двоичная информационная последовательность в цифровом виде, состоящая из символов «1» и «0». Последовательность поступала на вход цифрового блока NRZ кодера, где символ «0» заменялся на «-1», в результате чего получался двоичный цифровой сигнал с постоянными уровнями амплитуды +1 и -1.
Длительность одного бита двухуровневого цифрового сигнала Tб равнялась длительности эталонного фрагмента хаотического сигнала. С учетом временной синхронизации начала каждого бита с началом фрагмента хаотического сигнала, полученный двухуровневый сигнал перемножался с извлекаемым эталонным фрагментом хаоса. Между фрагментами выставлялся защитный интервал, длительностью равной длительности самого фрагмента (скважность 2). В результате перемножения формировался модулированный хаотический сигнал s(t).
Сформированный таким образом сигнал, поступал на адаптерный модуль NI FlexRIO, осуществляющий цифровую обработку сигналов с помощью ПЛИС. Этот модуль обеспечивал связь между цифровой и аналоговой частями системы, а также настройку параметров компонент аппаратной части. Программирование цифровой части, а также управление параметрами аналоговых компонент, настраиваемых при помощи ПЛИС, передатчика осуществлялось в среде программирования LabView.
Затем сигнал поступал на приемопередающий модуль для беспроводной связи NI 5791 с частотным диапазоном от 0,2 до 4,4 ГГц, где осуществлялось цифро-аналоговое преобразование. Полученный аналоговый сигнал, содержащий промодулированную хаосом информационную последовательность, фильтровался, усиливался и переносился вверх на частоту 2,47 ГГц. Далее сигнал излучался в эфир. Схема передатчика изображена на рис. 14а. Схема передатчика, отображенная в среде LabView, показана на рис. 14б.
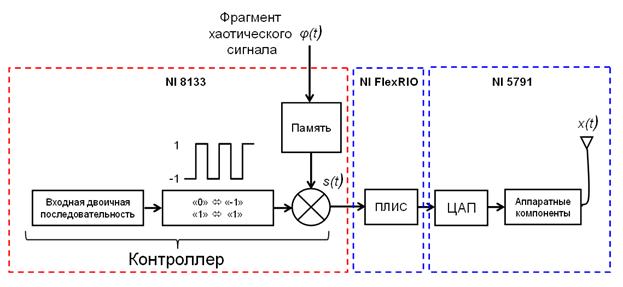
Рис. 14а. Передатчик когерентной схемы с одной базовой функцией в виде хаотического импульса.
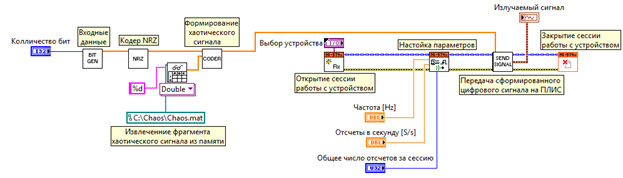
Рис. 14б. Схема элементов передатчика, отображенная в среде LabView.
На приемнике сигнал принимался антенной приемопередающего модуля NI 5791. На этом модуле сигнал усиливался, фильтровался и переносился вниз по частоте обратно в baseband диапазон, а затем оцифровывался с помощью АЦП. Далее через ПЛИС адаптерного модуля FlexRIO данный цифровой сигнал поступал на контроллер NI 8133, где производилась его окончательная обработка. Для обеспечения когерентного приема использовалась преамбула в виде стробирующего импульса, передаваемого перед началом посылки данных. Таким образом, производилась синхронизация по времени начала принимаемого цифрового сигнала, содержащего информационные данные с эталонным фрагментом хаотического сигнала, хранящегося в памяти контроллера приемника. Этот сигнал разбивался на отрезки длительности Tб, равные длительности эталонного фрагмента. С учетом скважности каждый полученный отрезок цифрового сигнала, содержащий информационный бит, поэлементно перемножался с эталонным фрагментом хаоса, а затем производилось интегрирование на всем временном интервале отрезка Tб. Решение, о значении принятого информационного символа – «1» или «0» выносилось на основе знака результата перемножения и интегрирования cor: cor > 0 соответствовал символу «1»; cor < 0 соответствовал символу «0». Из полученных символов составлялась выходная двоичная информационная последовательность. Схема приемника изображена на рис. 15а. Схема приемника, отображенная в среде LabView, показана на рис. 15б.
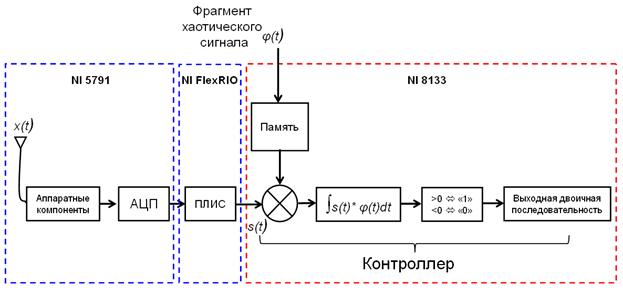
Рис. 15а. Приемник когерентной схемы с одной базовой функцией в виде хаотического импульса.
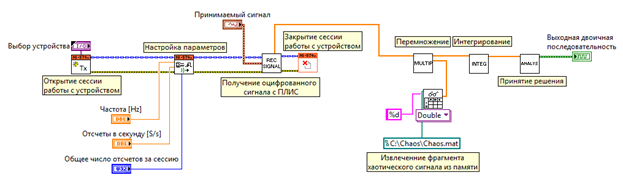
Рис. 15б. Схема элементов приемника, отображенная в среде LabView.
В эксперименте передавалась двоичная цифровая информационная последовательность. В результате работы построенной системы входная двоичная последовательность совпала со входной. На рис. 15 изображен передаваемый сигнал в baseband диапазоне (рис. 16а) перед преобразованием в аналоговый вид и построенный на основе входной двоичной последовательности двухуровневый сигнал (рис. 16б). На рис. 17 изображен передаваемый в baseband диапазоне сигнал (рис. 17а) перед преобразованием в аналоговый вид и построенный на основе выходной двоичной последовательности двухуровневый сигнал (рис. 17б).
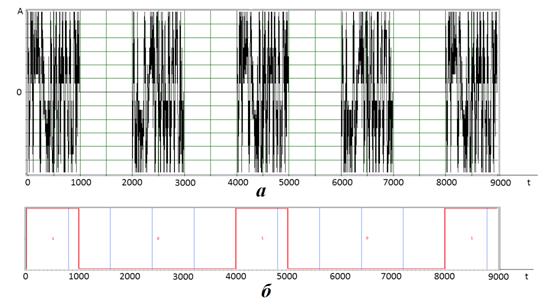
Рис. 16. а) Фрагмент сигнала,
полученный после перемножения двоичного цифрового сигнала
с постоянными
уровнями амплитуды с эталонным фрагментом хаотического сигнала;
б) двухуровневый
информационный сигнал в передатчике.
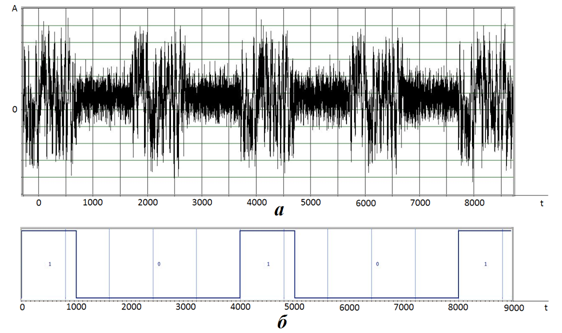
Рис. 17. а) Фрагмент сигнала на
выходе АЦП приемника;
б) двухуровневый информационный сигнал на приемнике
Выводы
В работе предложен метод когерентного приема и передачи информации с помощью хаотических импульсов. Когерентность обеспечивается за счет использования фрагментов хаотических сигналов фиксированной длительности цифровом виде, получаемых с помощью моделирования в среде Matlab и хранимых в памяти приемного и передающего устройств.
Была построена модель системы связи «точка-точка» в среде LabView с идеальным каналом связи, осуществляющая антиподальную моудялцию фрагмента хаотических колебаний двоичным информационным сигналом в baseband диапазоне, а также когерентный прием этого сигнала, где в качестве опорного сигнала приемника использовался такой же фрагмент хаотического сигнала. В результате моделирования входная двоичная информационная последовательность совпала с выходной.
Построенная модель послужила основой для построения когерентной системы передачи двоичной информации с помощью хаотических импульсов. Код модели в среде LabView использовался при построении блоков цифровой части приемника и передатчика. В качестве приемного и передающего устройств использовались макеты ПКР, собранные из модулей PXI компании National Instruments. Управление собранных макетов ПКР осуществлялось через интерфейс среды LabView.
Были проведены эксперименты, которые подтвердили возможность передачи информации через эфир предложенным способом с хорошим качеством.
Работа выполнена при частичной поддержке ФЦП ИР 2014-2020 Субсидия № 14.604.21.0036, идентификатор RFMEFI60414X0036
Литература
1) Partlitz U., Chua L., Kocarev L., Halle K., Shang A. “Transmission of digital signals by chaotic synchronization” // Int. J. Bifurcation and Chaos, 1992, V. 2, № 4, pp. 973-977.
2) Dedieu Н., Kennedy М., Hasler М. “Chaos shift keying: Modulation and demodulation of a chaotic carrier using self-synchronising Chua's circuits” // IEEE Trans. Circuits and Systems, 1993, V. CAS-40, № 10, pp. 634-642.
3) Dmitriev A., Panas A., Starkov S. “Transmission of complex analog signals by means of dynamical chaos” // Proc. NDES'95, 1995, Dublin, Ireland, pp. 241-244.
4) Волковский А.Р., Рульков Н.В. “Синхронный хаотический отклик нелинейной системы передачи информации с хаотической несущей” // Письма в ЖТФ, 1993, Т. 19, вып. 3, с. 71-75.
5) Pecora L.M. Carroll T.L. “Synchronization in Chaotic systems” // Phys. Rev. Lett., 1990, V. 64, № 8, pp. 821-824.
6) Kocarev L. and Partlitz U. “General approach for chaotic synchronization with application to communication” // Phys. Rev. Lett., 1995, V. 74, №25, pp. 5028-5031.
7) Кузьмин Л.В. «Беспроводная передача информация на сверхширокополосной хаотической несущей» // диссертация на соискание степени доктора физико-математических наук по специальности 01.04.03 «радиофизика», 401с., 2011.
8) Kis G., Jako Z., Kennedy M. P., and Kolumban G. "Chaotic communications without synchronization," // in Proc. 6th IEE Conf. Telecommunications, Edinburgh, U.K., Mar. 29-Apr. 1, 1998, pp. 49-53.
9) Kolumban G., Vizvari В., Schwarz W., and Abel A. "Differential chaos shift keying: A robust coding for chaotic communication," // in Proc. NDES'96, Seville, Spain, June 27-28, 1996, pp. 87-92.
10) Дмитриев А. С., Кузьмин Л.В., Панас А.И., Старков С. О., Пузиков Д.Ю., Ли Сеонг Су, Попов О.В. "Способ прямохаотической передачи информации с заданной спектральной маской" // Патент РФ № 2276458, приоритет от 26.11.2003 г.
11) Дмитриев А.С., Захарченко К.В., Пузиков Д.Ю. "Введение в теорию прямохаотической передачи информации" // Радиотехника и электроника, 2003, т. 48, №3, с. 328-338.
12) Dmitriev A., Panas A., Starkov S. “Transmission of complex analog signals by means of dynamical chaos” // Proc. NDES'95. 1995. Dublin, Ireland. pp. 241244.
13) Parlitz U. and Ergezinger S. “Robust Communications Based on Chaotic Spreading Sequences” //Phys. Lett. A., 1994, V. 188, pp. 146-150.
14) Дмитриев А.С., Панас А.И. «Динамический хаос. Новые носители информации для систем связи » // М.: Физматлит, 2002.
15) Силин А. «Технология Software Defined Radio. Теория, принципы и примеры аппаратных платформ» // Беспроводные технологии, №2, 2007.
16) “Технология программируемого радио на базе PXI” , National Instruments, URL: http://russia.ni.com/sites/default/files/%20NI%20для%20систем%20программируемого%20радио.pdf (Дата обращения 20.03.2015)
17) Сорохтин Е.М., Минеев С.А. "Распределенные программно-определяемые радиосистемы" // Вестник Нижегородского университета им. Н.И. Лобачевского, 2010, № 5 (2), с. 383–388.