УДК: 621.396.41

Разработка модели системы приема-передачи данных на основе сверхширокополосных сигналов

 

А. А. Капитанов¹, П. С. Остапенков¹, А. В. Скнаря ²

¹ Национальный исследовательский университет "МЭИ"

² Институт радиотехники и электроники им. В.А. Котельникова РАН

 

Статья получена  11 июня 2015 г.

 

Аннотация.  В статье рассматриваются вопросы, связанные с особенностями разработки в САПР ”Matlab” модели сверхширокополосной системы приема и передачи данных на основе сигналов с ортогональным частотным разделением каналов и учетом особенностей распространения сигналов в канале связи.

Ключевые слова: сверхширокополосные сигналы, широкополосные системы связи, разделение каналов, цифровая обработка широкополосных сигналов.

Abstract. This article describes the questions of ultrawideband communication system modeling based on the orthogonal frequency-division multiplexing (OFDM) channels.

Key words: ultrawideband signals, ultrawideband communication systems,  OFDM, digital signal processing of ultrawideband signals.

 

1.                Введение

В настоящее время сверхширокополосные сигналы широко используются в современных высокоскоростных системах связи стандартов WiMax, LTE, при передаче информации цифрового телевидения (DVB-T) и радио (DRM, DAB), в системах радиолокации и т.д. [1-3]. Использование  сигналов с ортогональным частотным разделением каналов (англ. Orthogonal frequency-division multiplexing, далее в тексте - OFDM) в системах передачи информации позволяет не только повысить информационную емкость системы при ограниченной полосе пропускания, но и скорость приема-передачи данных, приблизив её к пропускной способности канала, увеличить скрытность передачи и помехоустойчивость системы [4, 5].

При разработке системы приема передачи информации всегда приходится искать компромисс между такими параметрами системы как вид цифровой модуляции, число несущих в групповом спектре, величины частотного разноса несущих, длительностями защитного и рабочего интервалов информационного символа и некоторыми другими. Дополнительное влияние на параметры системы будет оказывать и канал связи. В этом случае моделирование системы передачи данных позволяет облегчить разработчику поиск наиболее оптимального решения для конкретной ситуации и провести анализ параметров модулей системы.

В представленной статье описываются особенности разработки модели системы приема-передачи информации на основе OFDM сигналов с различными видами цифровой модуляции и с учетом влияния параметров канала передачи.

Моделирование и расчеты системы и канала связи проводились в пакете ”Matlab”.

2. Структура сверхширокополосной системы на основе OFDM сигналов 

Системы с мультиплексированием с ортогональным частотным разделением каналов использует большое число ортогональных поднесущих, для каждой из которых возможно независимое применение различных схем модуляции и кодирования информационной последовательности.

При разработке модели системы с ортогональным частотным разделением каналов использовался низкочастотный эквивалент OFDM сигнала [1]:

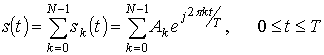,                                                             (1)                        

где k – индекс поднесущей, s_k(t) – сигнал на k-поднесущей, A_k – амплитудная составляющая последовательности информационных символов, N – количество поднесущих, T – длительность информационного символа.

При разработке OFDM систем передачи данных следует учитывать, что сигналы на k-поднесущих являются ортогональными на тактовом интервале T, но  ортогональность каждой из поднесущих напрямую связана со скоростью передачи данных, и в некоторых случаях спектры сигналов на каждой из поднесущих могут частично перекрываться. Многие OFDM сигналы изначально допускают частичное перекрытие спектров (например, QAM-4, QAM-16 и т.д.).

Эффективное использование спектра частот зависит от вида реализации детектирования данных: когерентное, некогерентное. В представленной модели  реализовано некогерентное детектирование [6].

Передатчик. Процесс формирования OFDM сигналов можно разделить на несколько стадий, которые хорошо реализуются независимо друг от друга как в аппаратной части, так и в плане использования алгоритмов [7].

Условно можно выделить пять основных этапов: преобразователь потока (“Serial to parallel unit”), цифровая модуляция (“Digital modulator”), вычисление обратного быстрого преобразования Фурье (“IFFT”), цифро-аналоговое преобразование (“DAC”), квадратурная модуляция (“Quadrature modulator”).

 

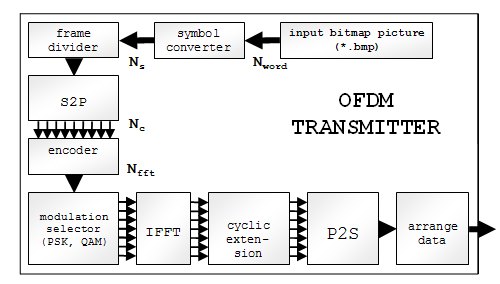
Рисунок 1. Структурная схема OFDM передатчика.

 

На рис. 1 представлена структурная схема модели OFDM передатчика, реализованная в пакете "Matlab". Рассмотрим назначение основных элементов системы на примере передачи графического изображения.

Входными данными являются файлы графических изображений в формате *.bmp с глубиной цветопередачи 8 бит в оттенках серого цвета. При таком представлении получается 256 оттенков серого цвета.

Декодирование графических изображений в оттенках серого цвета в модели осуществляется с помощью встроенной функции "imread.m" пакета "Matlab". Каждый пиксель переводится в однобайтовое слово, образуя двумерный массив. Высота исходной картинки h определяет количество строк, а ширина w – количество столбцов генерируемой матрицы. Матрица загружаемой картинки переводится в последовательный поток данных, при этом каждый элемент массива подвергается последовательному преобразованию из 8-битного формата в информационные символы (слова) заданного размера. Разрядность слова, кодирующего символа, зависит от выбора порядка модуляции, и возрастает с увеличением порядка модуляции. Для выполнения преобразования в модели используется функция "imgconv.m".

В блоке “symbol converter” матрица изображения перераспределяется на двоичные столбцы в соответствии с заданным порядком модуляции N_s и размером входного изображения N_w и преобразуется в вектор выходных символов  для требуемого типа модуляции. В этом случае размер вектора выходных символов определяться по формуле:

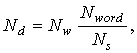                                                                                                      (2)

где  N_s – порядок модуляции, N_w – размер изображения на входе,  глубина графического изображения.

Далее проводится разбиение последовательности на необходимое количество символьных блоков и осуществляется их перевод в код, соответствующий глубине цветопередачи пикселя.

При преобразовании может возникнуть ситуация, когда какой-либо символ «выпал» из последовательности по причине большого уровня шума в канале. В этом случае выполняется алгоритм предсказания, который сравнивает текущий и последующий символы и заполняет пропущенные места оценочными значениями.

Затем символы в информационной последовательности разделяются на составные кадры OFDM передатчика в зависимости от переменной SpF (от англ. ”Symbol per Frame”). Переменная SpF определяет количество символов, приходящееся на одну поднесущую в каждом передаваемом кадре, и вычисляется по формуле [8]:

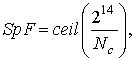                                                                                                      (3)

где ceil ­– функция “Matlab” округления в большую сторону,  – количество поднесущих.

Операцию упаковки символов в кадры поднесущих в OFDM модуляторе выполняет блок “frame divider”. Модулятор обрабатывает данные последовательно кадр за кадром. В случае, если длина информационной последовательности  не кратна выбранному количеству поднесущих , то последовательность в конце дополняется нулями.

В OFDM передатчике блок “S2P” (от англ. “serial-to-parallel”) переводит данные из последовательного потока в параллельный поток из  поднесущих.

Для улучшения параметров системы в схемах модуляторов передатчиков используют различные способы кодирования данных [1,5]. В представленной модели реализовано дифференциальное кодирование, которое осуществляется в блоке “encoder”.

На рис. 2. представлен фазовый спектр сигнала QAM-16 с учетом дифференциального кодирования.

При дифференциальном кодировании, в полученную ранее матрицу несущих, дополнительно добавляется проверочный вектор длиной , который может быть как набором случайных чисел, так и заданным набором значений.

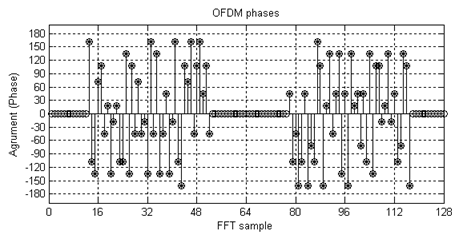
Рисунок 2. Фазовый спектр QAM-16 с дифференциальным кодированием.

Далее закодированные информационные слова преобразуются в соответствующие значения фаз и амплитуд. На этом этапе также происходит разделение потока на N_c поднесущих и задается тип модуляции – фазовая (PSK) или квадратурная амплитудная (QAM). Для уменьшения битовой ошибки информационные символы дополнительно кодируются кодом Грея.

Далее выполняется вычисление обратного быстрого преобразования Фурье (ОБПФ) в блоке “IFFT” в соответствии с заданным размером преобразования и количеством поднесущих N_c, заданных пользователем. В результате вычисления ОБПФ на выходе блока получаем один символьный период во временной области. Количество символьных периодов будет соответствовать количеству строк N_b в массиве передаваемых данных.

Для уменьшения уровня межсимвольных искажений к каждому полученному временному блоку добавляется некоторый локальный защитный интервал, представляющий циклический префикс, формируемый в блоке “cyclic extension” путём добавления определенного количества символов в начало последовательности информационного блока.

В блоке ”P2S” происходит преобразование N_b+1 строк двумерного массива в последовательность информационных блоков и глобальных защитных интервалов, которые формируются путем добавления отсчетов нулей между кадрами.

В блоке “arrange data” происходит упорядочивание полученной последовательности.

В итоге на выходе блока формируется низкочастотный эквивалент огибающей OFDM сигнала.

Приёмник. Все функции, выполняемые цифровыми блоками приемника, являются взаимно обратными тем операциям, которые проводились в передатчике и были описаны выше.

Рассмотрим назначение основных элементов OFDM приемника, структурная схема которого представлена на рис.3.

 

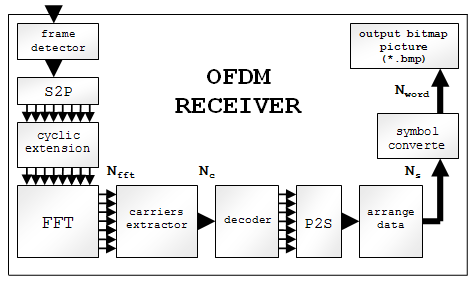
 Рисунок 3. Структурная схема OFDM приемника.

 

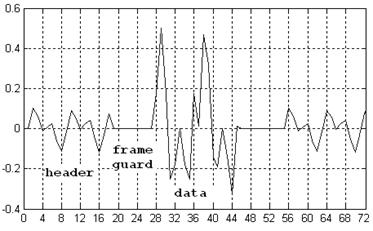
Рисунок 4. Последовательность из одного кадра.

 

В модели приемника ключевым блоком является детектор кадров “frame detector” принятой последовательности. Основное назначение детектора – синхронизация приема информационной последовательности на основе детектирования начала информационных символов из всей принимаемой последовательности. Помимо этой функции детектор кадров предназначен для отделения защитного интервала, заголовка и окончания кадра, удаления циклических префиксов во всем информационном блоке.

Пример одного информационного кадра представлен на рис. 4.

Для декодирования сигнала в приемнике определяется объем передаваемых данных по числу кадров N_f  принятой последовательности  [6]:

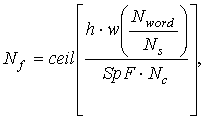                                                                          (4)

где h – высота изображения, w – ширина изображения, N_s – порядок цифровой модуляции.

Количество кадров прямо пропорционально объему передаваемой информации, который связан с размерами и глубиной цвета изображения, и обратно пропорционально порядку модуляции.

Уровень информационной части может в несколько раз превышать уровень заголовка сигнала и окончания кадра, как показано на рис. 4.  При этом глобальные защитные интервалы будут равны нулю, что позволяет различить и отбросить компоненты, не несущие в себе информации.

Для этого проводится поиск начала кадра, который можно разделить на несколько этапов. На первом этапе происходит вычисление модуля каждого отсчета последовательности и дискретизация кадра с шагом R_step, прямо пропорциональным длине БПФ. Далее данные пропускаются через цифровой фильтр, который детектирует положение нулевых значений до и после информационной части. После чего сигнал сдвигается на величину, определяемую отношением T_s/R_step (где T_s – символьный период), и повторно фильтруется.

В итоге определение положения начала кадра (фрейма) frame_loc можно рассчитать по формуле:

                                                           (5)

где idx – значение начала защитного интервала, погрешность оценки измерения защитного интервала сверху.

Поскольку фреймов в реальных системах может быть несколько, обобщим формулу на многокадровую систему:

                                        (6)

 

где R_{x_st} – номер фрейма.

Кадры (фреймы) последовательно обрабатываются с учетом того, что к первому был добавлен заголовок, а к последнему – окончание кадра.

OFDM демодулятор последовательно обрабатывает данные кадр за кадром. После определения положений начала и конца фреймов последовательный поток разделяется на параллельные, которые далее поступают на блок “cyclic extension”, где удаляются все защитные интервалы от информационной части сигнала.

Затем параллельно каждый из потоков данных поступает на блок прямого быстрого преобразования Фурье (БПФ), который переводит каждый информационный кадр в спектральные отсчеты. В зависимости от типа выбранной модуляции полезная информация может заключаться как в амплитуде и фазе сигнала (для сигналов QAM), так и только в фазе сигнала (для сигналов PSK).

В блоке “carriers extractor” происходит извлечение информации из каждой поднесущей для блока размером N_b. Алгоритмы получения полезной информации отличаются в зависимости от типа модуляции. При извлечении информации из каждой поднесущей действительная и мнимая компоненты спектральных отсчетов ставятся в соответствие с определенными эталонными значениями, полученными из кода Грея для конкретного типа и порядка модуляции.

Следует учесть, что в информационном потоке содержится набор нулей, необходимый модулятору для равномерного составления параллельного потока. Этот набор нулей удаляется в блоке ”arrange data”.

В блоке демодулятора “P2S” данные переводятся в последовательный вид, образуя итоговый информационный вектор, который далее поступает в блок “symbol converter”, где информационные символы преобразуются в "слова", конвертируемые затем в графическое изображение.

По итогам обработки данных приемником в модели предусмотрен вывод сигнальных созвездий по значениям действительной и мнимой компонент вектора кадра сигнала.

3. Особенности моделирования канала связи

Моделирование влияния канала связи является одной из важных задач, возникающих при моделировании системы приема-передачи данных. При моделировании каналов в воздушном пространстве обычно используют статистические модели.

В представленной модели расчеты проводились для двух типов каналов связи: для канала связи с аддитивным гауссовским белым шумом (AWGN) и для релеевского канала распространения сигнала. Отдельно в модели введен параметр усечения амплитуды сигнала в канале  - .

 Модель гауссовского канала может использоваться при оценке параметров канала связи с прямой видимостью передатчика и приемника при передаче сигналов без отражений и замираний, а также оценке влияния шумовой температуры приемника на параметры приема.

При учете шумовой составляющей в гауссовском канале дисперсия белого шума определяется по следующей формуле  [1]:

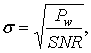                                                                                                   (7)

где  среднеквадратичное значение в канале, P_w – мощность сигнала, SNR – отношение сигнал-шум.

Величина отсечки в модели рассчитывается согласно [6]:

                                                                          (8)

где SC – амплитуда отсечки, CC – уровень отсечки в децибелах,  вектор передаваемой информационной последовательности.

Очевидно, что в реальной среде распространения за счет переотражений энергия сигнала будет распределяться неравномерно. Это явление получило название многолучевое распространение сигнала. Для учета таких параметров среды распространения как многолучевого распространения сигнала, интерференции в модели используется релеевский канал.

Использование релеевского канала целесообразно, когда между передатчиком и приемником нет прямой видимости. В этом случае энергия, принимаемая антенной, содержит много компонент, ни одна из которой не является доминирующей относительно других.

Релеевский канал используется при оценке параметров большинства мобильных устройств УКВ и GSM диапазонов.

В модели имеется возможность варьировать вероятное значение для получения оценок следующих параметров [6]:

- стандартной девиации         

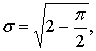                                                                                                 (9)

- функции плотности распределения вероятностей

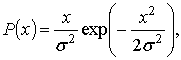                                                                                 (10)

- функции интегральной плотности

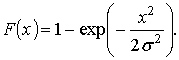                                                                               (11)

Рассмотрим более подробно основные результаты моделирования.

4. Результаты моделирования системы и канала связи

Исходными параметрами для модели являются: графическое изображение в оттенках серого с глубиной пикселя N_word = 8 бит, с размерами по высоте h = 512, ширине w = 512; варьируемые параметры модели - размерность БПФ N_FFT, количество поднесущих N_c, SNR, значения отсечки CC.

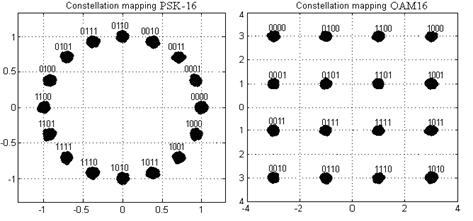
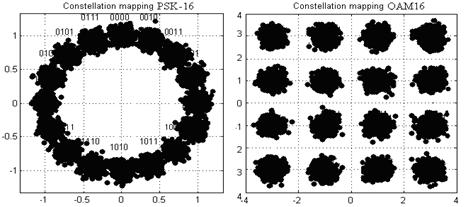
На рис. 5 показаны сигнальные созвездия для двух модуляций, соответственно,  PSK-16 и QAM-16 при разных значениях параметра сигнал-шум (SNR).

 

а).                                              б).

 

в).                                             г).

Рисунок 5. Сигнальные созвездия для:
а). PSK-16 (SNRdB = 20 дБ); б) QAM-16 (SNRdB = 20 дБ);
в) PSK-16 (SNRdB = 15 дБ); г) QAM-16 (SNRdB = 15 дБ).

На рис. 5  видно, что на сигнальном созвездии при уменьшении отношения сигнал-шум часть точек сдвигается на определенную величину, образуя при этом более размытое пятно в окрестности соответсвующих значений сигнала, что может привести к неправильной демодуляции данных и возникновению ошибочных значений в итоговой последовательности символов.

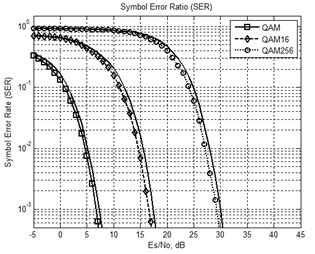
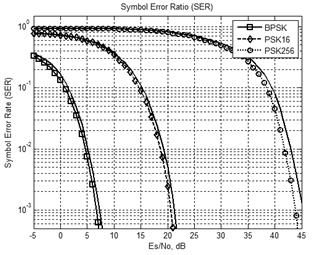
Для оценки параметров сигнала при передаче информации использовались зависимости символьной ошибки SER от энергии символа, отнесенной к спектральной плотности шума E_s/N₀ [9].

На рис. 6 представлены графики зависимости символьной ошибки от E_s/N₀ при разных типах модуляции (сплошными линиями показаны зависимости, построенные по справочным данным для соответствующих видов модуляций QAM, PSK [1]) . Как видно из графиков зависимости для символьной ошибки, полученные в модели, практически совпали с теоретическими.

 

a).                                                               б).

Рисунок 6. Зависимости символьной ошибки от типа модуляции:
а). QAM (N_s = 1, 4, 8); б). PSK (N_s = 1, 4, 8).

 

Из графиков рис.6 видно, что для более высоких порядков использование QAM модуляции будет более предпочтительным, чем PSK, поскольку ошибка демодулирования символа при фиксированном отношении энергии символа к плотности шума (E_s/N₀) будет меньше, поскольку в качестве модулируемого параметра выступает не только амплитуда, но и фаза. Для обеспечения более высокой скорости передачи необходимо повышать порядок модуляции, но это приводит к смещению характеристики SER вправо.

Помимо оценки вероятности символьной ошибки в моделируемую OFDM систему введена возможность оценить пиксельную ошибку для изображения.

Канал распространения. Канал распространения Релея отличается от гауссовского канала и позволяет оценить влияние интерференции и многолучевого распространения сигнала [10]. Рассмотрим зависимость символьной ошибки от отношения E_s/N₀ при использовании гауссова и релеевского каналов передачи.  

На рис. 7 представлена зависимость символьной ошибки SER от E_s/N₀ для OFDM системы с учетом канала распространения сигналов Гаусса и Релея (оценки параметров для канала Релея носят статистический характер, поэтому на графике показана усредненная зависимость) при следующих параметрах исходных данных: N_FFT = 4096, тип модуляции – BPSK, QAM-16, количество поднесущих N_c =1013.

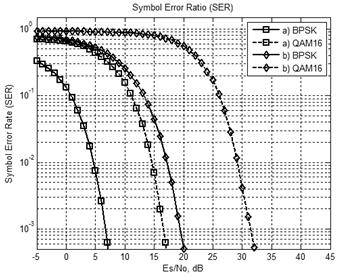
Рисунок 7. Символьная ошибка для BPSK, QAM-16 при разных моделях канала распространения: (a) Гаусса; (b) Релея.

Из рис.7 видно, что при использовании модели канала Релея происходит смещение зависимостей вправо. Для сравнения при фиксированном E_s/N₀ такое смещение может приводить к увеличению количества ошибочных детектированных символов по сравнению с гауссовым каналом распространения.

5. Заключение

В статье описана математическая модель системы связи в пакете ”Matlab”, позволяющая проводить качественную и количественную оценку передачи OFDM сигналов.

Моделирование системы проводились на примере передачи черно-белого изображения с учетом таких параметров системы как скорость передачи, параметры модуляции, величина канальной отсечки, уровень шума, способа кодирования сигнала, а также учитывалось влияние канала распространения сигнала.

Предложенные в статье подходы могут быть использованы при реализации и моделировании широкополосных систем приема-передачи информации с различными способами кодирования, а также при оценке влияния на распространение OFDM сигналов параметров каналов связи Гаусса и Релея.

 

Литература

1.                 Скляр Б. Цифровая связь. Теоретические основы и практическое применение. Пер. с англ. М.: Издательский дом «Вильямс», 2003. – 1104 с.

2.                 Витакре Ян. FDMA с одной несущей - новый восходящий канал LTE. //  Электронные компоненты. №2, 2007. с.46-49.

3.                 Ultra-wideband Wireless Communications and Networks Edited by Xuemin Shen et.al. USA: John Wiley & Sons, 2006. – 310 p.

4.                 Bernardo L., Lopes P.B. Quadrature chaotic symbolic OFDM communication over radio channels / "Communications (LATINCOM) – 2012. IEEE Latin-America Conference", pp.1-6, 2012.

5.                 Al-Mahmoud M., Zoltowski M.D. Performance evaluation of Code-Spread OFDM with error control coding / "Military Communications Conference – 2008 (IEEE MILCOM 2008) ". pp.1-6, 2008.

6.                 Прокис Дж. Цифровая связь. Пер. с англ. // Под ред. Д. Д. Кловского. М.: Радио и связь, 2000. – 800 с.

7.                 Феер К. Беспроводная цифровая связь: методы модуляции. Пер. с англ. // Под. ред. В. И. Журавлёва. М.: Радио и связь, 2000. – 520 с.

8.                 Dogan H., Yildiz H., Cooklev T., Acar Y. Coded OFDM wireless systems with generalized prefix /"Application of Information and Communication Technologies (AICT) ", 2012 6th International Conference., pp.1-4. 2012.

9.                 Вишневский В.М., Ляхов А.И., Портной С.Л., Шахнович И.В. Широкополосные беспроводные сети передачи информации. М.: Техносфера, 2005. – 592 с.

10.            Chenggao Han, Hashimoto T., Suehiro N. Constellation-rotated vector OFDM and its performance analysis over Rayleigh fading channels / Communications, IEEE Transactions, vol.58, no.3, pp.828-838, 2010.