УДК 537.525.6 : 621.372.826
МУЛЬТИПАКТОРНЫЙ РАЗРЯД В ПРЯМОУГОЛЬНЫХ
ВОЛНОВОДАХ ВЫВОДА ЭНЕРГИИ МОЩНЫХ ЭВП СВЧ
А. В. Егоров, М. А. Мартыненко, Б. В. Прокофьев
ФГУП НПП «Торий», Москва
Статья получена 27 мая 2015 г.
Аннотация. Представлены результаты исследования условий возникновения мультипакторного разряда в прямоугольных волноводах вывода энергии мощных ЭВП СВЧ в присутствии магнитных полей рассеяния фокусирующей системы. С учетом функций распределения электронов по скоростям вылета и кривой коэффициента вторичной эмиссии для бескислородной меди найдены соотношения размеров стенок прямоугольных волноводов, при которых возможен разряд в отсутствие постоянного магнитного поля.
Ключевые слова: мультипакторный разряд, прямоугольный волновод, статическое магнитное поле, электровакуумный прибор СВЧ.
1. Введение
При работе мощных электровакуумных приборов СВЧ порой наблюдается аномальный нагрев вакуумированного медного волновода, соединяющего систему отбора энергии электронного пучка с окном вывода энергии. Причиной этого нагрева является мультипакторный разряд (МР), возникающий в волноводе при передаче высоких уровней мощности. Разряд в волноводах исследовался в ряде работ [1-6], в том числе, с применением методов компьютерного моделирования [2-6], причем основной целью этих исследований был анализ условий возникновения МР в электродинамических системах ускорителей элементарных частиц и установок термоядерного синтеза (токамаков) с учетом особенностей технологии и функционирования этих устройств. Так, волноводные устройства, рассмотренные в [2], проходят обезгаживание в вакууме при температуре около 200°С, а в дальнейшем работают при криогенных температурах. В других случаях температура отжига волноводов не превышает 240°С [6]. В то же время электровакуумные приборы СВЧ в процессе откачки поддерживают при температуре около 550°С, а при работе приборов температура волноводов может лишь в той или иной степени превышать температуру окружающей среды (например, за счет нагрева, вызванного омическими потерями и токооседанием в системе отбора энергии прибора). В результате, например, коэффициент вторичной электронной эмиссии (КВЭЭ) меди может изменяться в пределах от 1,1 до 2,3 [7]. Отличия в режимах технологической обработки волноводов и в условиях их последующей эксплуатации приводит к значительным разбросам величины КВЭЭ их стенок. При рассмотрении поведения заряженных частиц в волноводе вывода энергии прибора следует также учитывать, что в ЭВП СВЧ выходной волновод находится в полях рассеяния магнитной фокусирующей системы, величина которых может изменяться по длине волновода, а направление – зависеть от конкретной конструкции выходного устройства. Цель работы состояла в создании математической модели, алгоритма и программы расчета МР в электромагнитном поле бегущей волны Н10 прямоугольных волноводов и исследовании условий возникновения разряда в выводах энергии мощных электровакуумных приборов СВЧ с учетом возможных направлений постоянного магнитного поля по отношению к волноводу, соединяющему выход прибора с вакуумноплотным окном.
2. Методика моделирования МР в прямоугольном волноводе
Для моделирования мультипакторного разряда обычно используют 3D программы, позволяющие рассчитать
методом ”particle-in-cell” траектории
заряженных частиц в электромагнитных полях электродинамических систем практически
любой формы. В то же время, как справедливо отмечается в работе [6], сочетание
стохастических процессов, присущих вторичной эмиссии, с шумами, характерными
для PIC-методов вычислений, неизбежно
отражается на погрешности определения порога МР. Между тем в прямоугольном
волноводе электромагнитное поле волны Н10 описывается простыми
аналитическими выражениями, использование которых позволяет уменьшить
погрешность вычислений при определении скоростей и траекторий электронов в
волноводе, а также уменьшить затраты времени на проведение расчетов. Уравнения
движения электрона в поле волны Н10 прямоугольного волновода и
произвольно направленном постоянном магнитном поле ![]() рассеяния фокусирующих магнитов вакуумного
СВЧ прибора имеют следующий вид:
рассеяния фокусирующих магнитов вакуумного
СВЧ прибора имеют следующий вид:
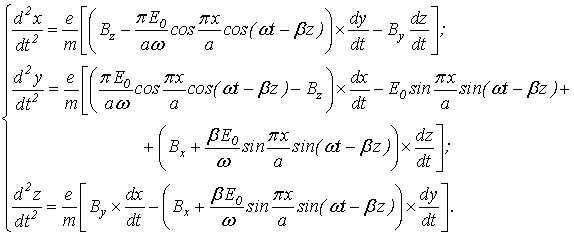
Здесь ![]() – амплитуда электрического поля в
Е-плоскости прямоугольного волновода,
– амплитуда электрического поля в
Е-плоскости прямоугольного волновода, ![]() – круговая частота,
– круговая частота, ![]() – ширина волновода,
– ширина волновода, ![]() –
постоянная распространения волны Н10 в волноводе,
–
постоянная распространения волны Н10 в волноводе, ![]() – продольная координата,
– продольная координата, ![]() – координата, направленная вдоль
широкой стенки волновода,
– координата, направленная вдоль
широкой стенки волновода, ![]() – пространственные компоненты постоянного магнитного поля
– пространственные компоненты постоянного магнитного поля ![]() . Магнитное поле волны Н10 с учетом уравнений
Максвелла выражено через электрическое СВЧ поле. Для решения уравнений
использовалась схема «3/8» метода Рунге-Кутты 4-го порядка, позволяющая
минимизировать как погрешность вычислений, так и затраты времени на проведение
расчетов.
. Магнитное поле волны Н10 с учетом уравнений
Максвелла выражено через электрическое СВЧ поле. Для решения уравнений
использовалась схема «3/8» метода Рунге-Кутты 4-го порядка, позволяющая
минимизировать как погрешность вычислений, так и затраты времени на проведение
расчетов.
С помощью программы SMRW (Simulation of Multipactor in Rectangular Waveguides), реализованной в среде VisualC# на базе разработанной математической
модели, были исследованы условия возникновения МР в диапазоне мощностей 10
кВт÷100 МВт в волноводе c
размером широкой стенки а=72 мм на частоте f=3 ГГц. При проведении расчетов предполагалось, что прямоугольный
волновод изготовлен из бескислородной меди, в процессе откачки прибора отожженной
при температуре 550°С (максимальная
величина КВЭЭ ![]() меди равна 1,45 [8]), или
нержавеющей стали (
меди равна 1,45 [8]), или
нержавеющей стали (![]() [9]).
[9]).
Начальная отладка программы проводилась на примере решения
задачи о движении одиночного электрона в электромагнитном поле волны H10 прямоугольного волновода сечением ![]() мм2 при величине передаваемой мощности
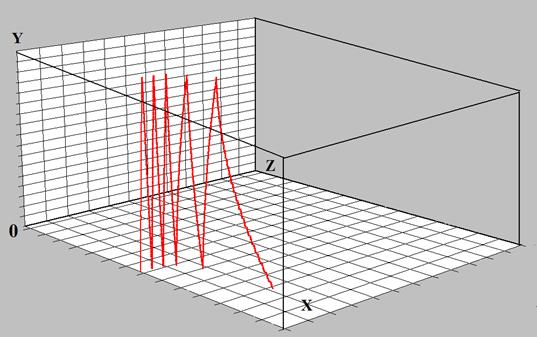
600 кВт. Траектория электрона, покидающего поверхность волновода с энергией,
равной 3 эВ, перпендикулярно широкой стенке на расстоянии 0,1 мм от ее середины
в направлении оси x, приведена на
рис. 1. КВЭЭ поверхностей волновода условно принят равным единице.
мм2 при величине передаваемой мощности
600 кВт. Траектория электрона, покидающего поверхность волновода с энергией,
равной 3 эВ, перпендикулярно широкой стенке на расстоянии 0,1 мм от ее середины
в направлении оси x, приведена на
рис. 1. КВЭЭ поверхностей волновода условно принят равным единице.
|
Рис. 1. Траектория электрона в поле волны Н10 прямоугольного волновода. Волна распространяется в направлении оси Z. |
В электромагнитном поле волны Н10 электрон дрейфует в направлении вектора Пойнтинга под действием высокочастотного магнитного поля. Эффект перемещения электронов по направлению распространения волны в волноводе был впервые рассмотрен в работах Ф. Крайнена [10,11] и получил название «электронного ветра».
Для описанных стартовых условий скорость дрейфа электрона,
находящегося вблизи Е-плоскости волновода, в z-направлении линейно возрастает с увеличением передаваемой
мощности и составляет около ![]() м/c при передаче мощности, равной 1 МВт. Отметим, что траектория электрона,
представленная на рис. 1, в проекции на плоскость поперечного сечения волновода
имеет вид, аналогичный рассчитанному в работе [4]. Под
действием z-составляющей высокочастотного магнитного
поля электрон отклоняется к боковой стенке волновода и попадает в область более
слабых электрических полей, теряя энергию и переставая участвовать в процессе умножения
числа частиц. Скорость дрейфа электрона в
поперечном направлении может превышать скорости дрейфа вдоль волновода
приблизительно в 3-15 раз при запусках электрона на расстоянии от 1 до 10 мм от
середины широкой стенки волновода. Такая потеря электронов из разряда должна
затруднить или сделать невозможным возникновение МР. Однако факт существования МР
в волноводах имеет экспериментальные подтверждения [5,12]. Это обстоятельство и
придает актуальность исследованиям МР в волноводах выводов энергии мощных ЭВП
СВЧ.
м/c при передаче мощности, равной 1 МВт. Отметим, что траектория электрона,
представленная на рис. 1, в проекции на плоскость поперечного сечения волновода
имеет вид, аналогичный рассчитанному в работе [4]. Под
действием z-составляющей высокочастотного магнитного
поля электрон отклоняется к боковой стенке волновода и попадает в область более
слабых электрических полей, теряя энергию и переставая участвовать в процессе умножения
числа частиц. Скорость дрейфа электрона в
поперечном направлении может превышать скорости дрейфа вдоль волновода
приблизительно в 3-15 раз при запусках электрона на расстоянии от 1 до 10 мм от
середины широкой стенки волновода. Такая потеря электронов из разряда должна
затруднить или сделать невозможным возникновение МР. Однако факт существования МР
в волноводах имеет экспериментальные подтверждения [5,12]. Это обстоятельство и
придает актуальность исследованиям МР в волноводах выводов энергии мощных ЭВП
СВЧ.
Дальнейшее моделирование МР проводилось на основе метода
Монте-Карло с использованием нормированной функции распределения электронов по
скоростям вылета ![]() , предложенной в работе [13]:
, предложенной в работе [13]:
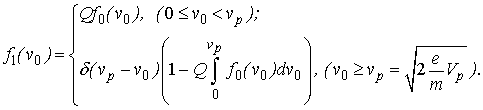
Здесь ![]() – величина скорости первичных электронов;
– величина скорости первичных электронов; ![]() – функция Дирака:
– функция Дирака:
![]() – константа, определяющая долю упруго отраженных электронов в общем числе
вторичных электронов;
– константа, определяющая долю упруго отраженных электронов в общем числе
вторичных электронов; ![]() – энергия первичного электрона.
В приведенном выражении для
– энергия первичного электрона.
В приведенном выражении для ![]() использована отличная от максвелловской функция
распределения по скоростям вылета частиц
использована отличная от максвелловской функция
распределения по скоростям вылета частиц
![]()
(где![]() – наивероятнейшая скорость вылета
электрона, соответствующая энергии 2÷3 эВ), которая позволяет более
точно описать «хвост» неупруго отраженных электронов. Записанная в предлагаемом
виде функция распределения по скоростям вылета учитывает все виды вторичных
электронов, включая и упруго отраженные, причем, в соответствии с данными
измерений [14], число упруго отраженных электронов растет при уменьшении
энергии первичных частиц.
– наивероятнейшая скорость вылета
электрона, соответствующая энергии 2÷3 эВ), которая позволяет более
точно описать «хвост» неупруго отраженных электронов. Записанная в предлагаемом
виде функция распределения по скоростям вылета учитывает все виды вторичных
электронов, включая и упруго отраженные, причем, в соответствии с данными
измерений [14], число упруго отраженных электронов растет при уменьшении
энергии первичных частиц.
Распределение частиц по направлениям вылета предполагалось
косинусоидальным, а КВЭЭ ![]() для медных стенок волновода рассчитывался по формулам
работы [8], аппроксимирующим экспериментальную зависимость
для медных стенок волновода рассчитывался по формулам
работы [8], аппроксимирующим экспериментальную зависимость ![]() :
:
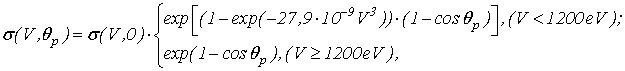
где ![]() – угол падения первичного электрона. Для расчета коэффициента вторичной эмиссии при нормальном
падении электрона на поверхность использовалось обобщение полуэмпирической
формулы Стернгласса [14], предложенное в работе [13]:
– угол падения первичного электрона. Для расчета коэффициента вторичной эмиссии при нормальном
падении электрона на поверхность использовалось обобщение полуэмпирической
формулы Стернгласса [14], предложенное в работе [13]:
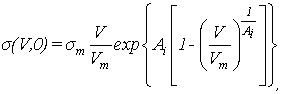
где ![]() – энергия первичных электронов в точке
максимума КВЭЭ
– энергия первичных электронов в точке
максимума КВЭЭ ![]() материала;
материала; ![]() – постоянные, подбираемые отдельно для
нарастающего и ниспадающего участков измеренной кривой КВЭЭ. Функция
– постоянные, подбираемые отдельно для
нарастающего и ниспадающего участков измеренной кривой КВЭЭ. Функция ![]() непрерывна вместе с первой производной в
точке
непрерывна вместе с первой производной в
точке ![]() . Для рассматриваемого случая
. Для рассматриваемого случая ![]() (в формуле Стернгласса
(в формуле Стернгласса ![]() ).
).
В работе сделана попытка учета в простейшем виде статистики вторичной электронной эмиссии, а именно, целого числа электронов, рождающихся в процессе каждого соударения, тогда как величина КВЭЭ, вообще говоря, не является целочисленной. Число выбитых электронов выбиралось из двух целочисленных значений, ближайших к величине коэффициента вторичной эмиссии, таким образом, что вероятность выбора каждого из этих значений пропорциональна разности между вторым целым числом и величиной КВЭЭ, получившейся при соударении электрона со стенкой волновода. В случаях, когда целое число оказывалось равным нулю, новые электроны не эмитировались, а программа переходила к расчету следующих частиц.
Разработанный алгоритм также позволяет отслеживать выполнение закона сохранения энергии при розыгрыше каждого соударения. Если суммарная энергия выбитых электронов превышает энергию первичного электрона, то розыгрыш соударения повторяется до тех пор, пока начальная энергия всех вторичных электронов не окажется меньше энергии первичного электрона.
Возможность существования МР определялась величиной
эффективного (среднего) КВЭЭ ![]() , представляющего собой отношение количества всех вторичных электронов к числу
всех первичных по прошествии времени, необходимого для «выстраивания» процесса МР
безотносительно к изначально навязанным условиям запуска затравочных электронов.
Разряд возможен, если
, представляющего собой отношение количества всех вторичных электронов к числу
всех первичных по прошествии времени, необходимого для «выстраивания» процесса МР
безотносительно к изначально навязанным условиям запуска затравочных электронов.
Разряд возможен, если ![]() Для удобства анализа траекторий
электронов запуск затравочных электронов производился с одной из широких стенок
в плоскости XY поперечного сечения волновода. Точки эмиссии затравочных электронов
генерировались случайным образом и располагались на широких стенках волновода
вдоль прямой линии, параллельной оси Х. Электроны эмитировались с шагом,
равным
Для удобства анализа траекторий
электронов запуск затравочных электронов производился с одной из широких стенок
в плоскости XY поперечного сечения волновода. Точки эмиссии затравочных электронов
генерировались случайным образом и располагались на широких стенках волновода
вдоль прямой линии, параллельной оси Х. Электроны эмитировались с шагом,
равным ![]() ,
в интервале фаз от 0 до 360˚ с начальными скоростями,
соответствующими энергии 3 эВ. Число затравочных электронов составляло от 1000
для резонансных видов разряда до 10000 для нерезонансных (т. н. «полифазных» [8])
видов МР.
,
в интервале фаз от 0 до 360˚ с начальными скоростями,
соответствующими энергии 3 эВ. Число затравочных электронов составляло от 1000
для резонансных видов разряда до 10000 для нерезонансных (т. н. «полифазных» [8])
видов МР.
3. Результаты анализа условий существования МР в выходных волноводах ЭВП СВЧ
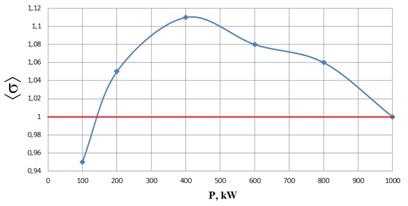
Проведенные расчеты показали, что в отсутствие постоянного
магнитного поля ![]() в прямоугольном волноводе
в прямоугольном волноводе ![]() мм2 из нержавеющей стали мультипакторный
разряд возможен в диапазоне передаваемых мощностей от 150 до 1000 кВт (рис. 2),
что соответствует интервалу напряженностей электрического поля в Е-плоскости
волновода от 3,5 до 9,2 кВ/мм. Полученный диапазон напряженностей близок к
экспериментальным данным (нижний порог разряда 5 кВ/мм, верхний порог – 8,5
кВ/мм), приведенным в работе [12].
мм2 из нержавеющей стали мультипакторный
разряд возможен в диапазоне передаваемых мощностей от 150 до 1000 кВт (рис. 2),
что соответствует интервалу напряженностей электрического поля в Е-плоскости
волновода от 3,5 до 9,2 кВ/мм. Полученный диапазон напряженностей близок к
экспериментальным данным (нижний порог разряда 5 кВ/мм, верхний порог – 8,5
кВ/мм), приведенным в работе [12].
|
|
|
Рис. 2. Зависимость величины |
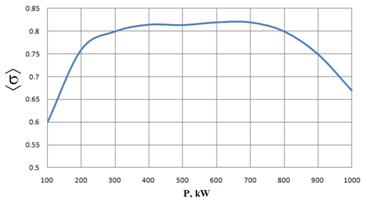
Для такого же медного волновода, находящегося вне зоны
действия поля фокусирующих магнитов, эффективный КВЭЭ в интервале мощностей Р=(100÷1000)
кВт не превысил величины 0,82 (рис. 3). Коэффициент вторичной эмиссии меди меньше
КВЭЭ стали и недостаточно велик для того, чтобы компенсировать уход частиц к
боковым стенкам в область слабых электрических полей. Разряд в медном волноводе
сечением ![]() мм2, прошедшем стандартную технологическую
обработку в составе ЭВП СВЧ, оказывается, таким образом, невозможным.
мм2, прошедшем стандартную технологическую
обработку в составе ЭВП СВЧ, оказывается, таким образом, невозможным.
|
|
|
Рис. 3. Зависимость
эффективного КВЭЭ |
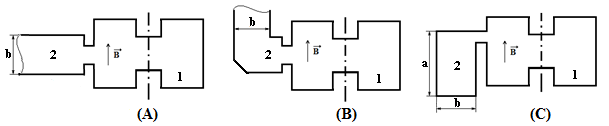
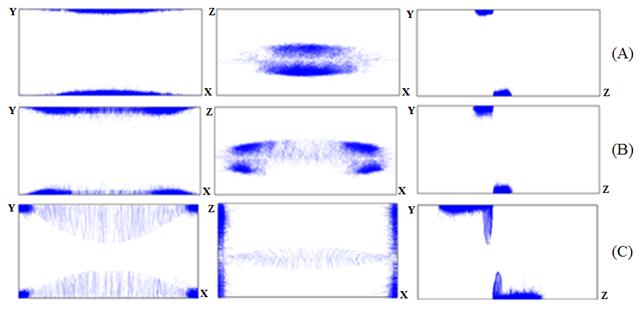
Влияние статических магнитных полей, создаваемых фокусирующей системой прибора, исследовалось для трех вариантов взаимного расположения выходного резонатора 1 и прямоугольного волновода 2 (рис. 4). Редко встречающаяся на практике конфигурация, показанная на рис. 4C, может применяться в вертикально установленных приборах с целью увеличения электрической прочности невакуумного тракта, в котором инициирующие пробой частицы пыли оседают на узкую стенку волновода в области нулевого электрического поля.
|
|
|
Рис. 4. Возможные варианты расположения прямоугольного волновода 2 относительно
фокусирующего магнитного поля
|
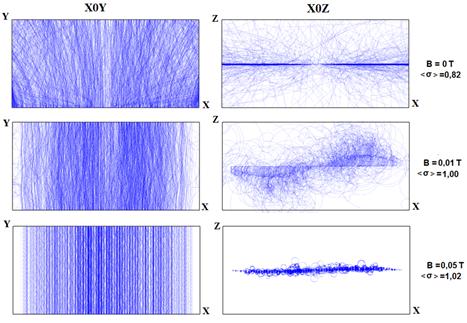
На рис. 5 представлены результаты моделирования траекторий электронов в медном прямоугольном волноводе в зависимости от величины внешнего статического магнитного поля, совпадающего по направлению с высокочастотным электрическим полем (рис. 4А). Расчет проводился для величины передаваемой мощности 600 кВт, которой соответствует амплитуда индукции магнитного СВЧ поля, равная 0,0023 Тл.
|
|
|
Рис. 5. Траектории электронов в прямоугольном волноводе при разных величинах постоянного магнитного поля, перпендикулярного широким стенкам волновода, в проекции на плоскости x0y и x0z. |
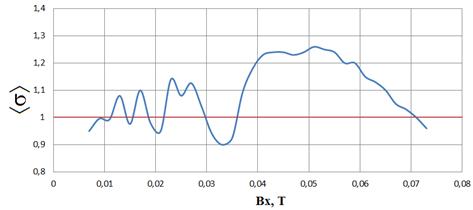
Статическое магнитное поле препятствует дрейфу электронов
вдоль волновода и их уходу на боковые стенки под влиянием высокочастотного
магнитного поля волны Н10. Как следствие, при магнитной индукции
постоянного поля более 0,01 Тл эффективный КВЭЭ может превысить единицу ![]() и в медном волноводе оказывается
возможным возникновение двухповерхностного полифазного МР в широком интервале
мощностей от 200 кВт до 50 МВт (рис. 6). Однако превышение величиной
и в медном волноводе оказывается
возможным возникновение двухповерхностного полифазного МР в широком интервале
мощностей от 200 кВт до 50 МВт (рис. 6). Однако превышение величиной ![]() пороговой величины
пороговой величины ![]() в указанном диапазоне мощностей не
превышает 7%. Между тем, согласно экспериментальным данным[1] для
нерезонансных (полифазных) видов разряда после включения СВЧ мощности порог МР постепенно
повышается на 10-20% за счет интенсивного обезгаживания поверхностного и
приповерхностного слоев материала под действием электронной бомбардировки.
Поэтому следует ожидать, что ввиду сильной зависимости рассматриваемого разряда
от состояния поверхности и качества материала волновода этот вид МР может
оказаться неустойчивым.
в указанном диапазоне мощностей не
превышает 7%. Между тем, согласно экспериментальным данным[1] для
нерезонансных (полифазных) видов разряда после включения СВЧ мощности порог МР постепенно
повышается на 10-20% за счет интенсивного обезгаживания поверхностного и
приповерхностного слоев материала под действием электронной бомбардировки.
Поэтому следует ожидать, что ввиду сильной зависимости рассматриваемого разряда
от состояния поверхности и качества материала волновода этот вид МР может
оказаться неустойчивым.
|
|
|
Рис. 6. Зависимость
эффективного КВЭЭ
|
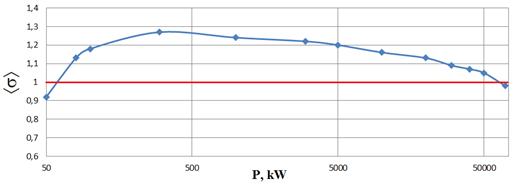
На рис. 7А представлены результаты расчета траекторий
электронов в постоянном магнитном поле величиной В=0,053 Тл, направленном
вдоль прямоугольного волновода. Указанной величине магнитной индукции
соответствует циклотронная частота, равная половине частоты СВЧ поля ![]() . При этом углы пролета электронов с
момента эмиссии до возвращения на поверхность волновода кратны
. При этом углы пролета электронов с
момента эмиссии до возвращения на поверхность волновода кратны ![]() . Если энергия V электронов лежит в
интервале
. Если энергия V электронов лежит в
интервале ![]() (где
(где ![]() – энергии,
соответствующие первому и второму критический потенциалы материала стенок волноводов),
то оказываются выполненными условия существования одноповерхностного резонансного
МР [15]. Под действием постоянного продольного магнитного поля частицы
дрейфуют в направлении одной из боковых стенок волновода. В интервале мощностей
от 110 кВт до 760 кВт при постоянной подпитке затравочными электронами, эффективный
КВЭЭ превышает единицу (рис. 7B), однако постоянный отток электронов в область слабых электрических полей должен затруднять
возникновение разряда. Тем не менее, принимая во внимание, что число последовательных
актов умножения электронов за счет соударения с широкой стенкой волновода
достигает 20-30, нельзя полностью исключить возможность
существования индуцированного МР при достаточном количестве затравочных
электронов. Наиболее вероятной причиной появления затравочных электронов может
быть фотоэффект, обусловленный рентгеновским излучением из коллектора и
предколлектора прибора [9].
– энергии,
соответствующие первому и второму критический потенциалы материала стенок волноводов),
то оказываются выполненными условия существования одноповерхностного резонансного
МР [15]. Под действием постоянного продольного магнитного поля частицы
дрейфуют в направлении одной из боковых стенок волновода. В интервале мощностей
от 110 кВт до 760 кВт при постоянной подпитке затравочными электронами, эффективный
КВЭЭ превышает единицу (рис. 7B), однако постоянный отток электронов в область слабых электрических полей должен затруднять
возникновение разряда. Тем не менее, принимая во внимание, что число последовательных
актов умножения электронов за счет соударения с широкой стенкой волновода
достигает 20-30, нельзя полностью исключить возможность
существования индуцированного МР при достаточном количестве затравочных
электронов. Наиболее вероятной причиной появления затравочных электронов может
быть фотоэффект, обусловленный рентгеновским излучением из коллектора и
предколлектора прибора [9].
|
|
|
Рис. 7. Распределение электронов в разряде при направлении постоянного
магнитного поля ( |
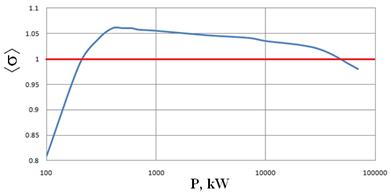
Для конфигурации, показанной на рис. 4С, при той же величине постоянного магнитного поля условия существования МР выполняются в широком диапазоне мощностей, примерно от 50 кВт до 60 МВт (рис. 8).
|
|
|
Рис. 8. Зависимость
эффективного КВЭЭ |
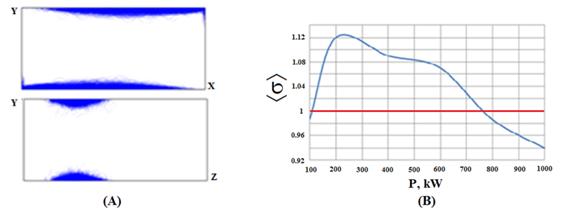
При мощности, составляющей несколько сотен кВт, разряд сосредоточен преимущественно в центральной части волновода (рис. 9A). С увеличением мощности область разряда начинает смещаться к боковым стенкам (рис. 9B), т.к. при соударении электронов с центральной частью широкой стенки волновода их энергия начинает превышать второй критический потенциал меди, равный 2 кВ. При уровнях передаваемой мощности в несколько десятков МВт одноповерхностный МР переходит в область между боковой и широкой стенками волновода (рис. 9C).
|
|
|
Рис. 9. Распределение электронов в разряде при направлении постоянного
магнитного поля ( |
Расчет зависимости пороговой мощности разряда от величины внешнего магнитного поля показал, что МР может существовать и в области частот, кратных удвоенной или учетверенной циклотронной частоте (рис. 10). Следует отметить, что возможность существования таких зон разряда была предсказана авторами работы [15], разработавшими теорию МР в скрещенных полях. В приведенном примере, как и в примерах, рассмотренных выше (рис. 5,7,9), в целях удобства анализа запуск затравочных электронов осуществлялся вдоль линии, параллельной оси 0X.
Моделирование результатов, полученных в настоящей работе, на
другие диапазоны частот может осуществляться с учетом того факта, что энергия
электронов в разряде определяется величиной проходящей по волноводу мощности и
размерами поперечного сечения волновода. Поэтому для геометрически подобных
волноводов, поперечные размеры которых изменяются обратно пропорционально
частоте, пороговые мощности МР будут оставаться неизменными,
если неизменным остается соотношение рабочей и циклотронной частот:![]() . Это правило моделирования было нами
проверено на примере трех
стандартных волноводов с близким соотношением сторон
. Это правило моделирования было нами
проверено на примере трех
стандартных волноводов с близким соотношением сторон ![]() (
(![]() мм2,
мм2, ![]() мм2
и
мм2
и ![]() мм2) для конфигураций вывода
энергии, представленных на рис. 4, и полностью подтвердилось.
мм2) для конфигураций вывода
энергии, представленных на рис. 4, и полностью подтвердилось.
|
|
|
Рис. 10. Зависимость эффективного КВЭЭ от величины индукции постоянного
магнитного поля |
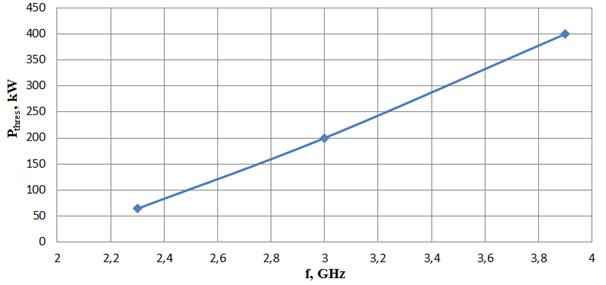
В то же время следует учитывать, что порог МР может заметно
изменяться с частотой при неизменных размерах волновода. Так, для основной
конфигурации (рис. 4А) и волновода сечением ![]() мм2
пороговая мощность МР практически линейно зависит от частоты и имеет вид,
представленный на рис. 11.
мм2
пороговая мощность МР практически линейно зависит от частоты и имеет вид,
представленный на рис. 11.
Для увеличения связи выходной цепи с выходным резонатором или облегчения проводки вывода энергии через магнитную фокусирующую систему в электровакуумных приборах часто используют волноводы уменьшенной высоты. Уменьшение высоты должно приводить к росту числа соударений электронов с широкими стенками волновода до того, как под действием магнитного СВЧ поля электроны переместятся в область слабого электрического поля вблизи боковых стенок волновода. В этом случае увеличение доли электронов, рождающихся в области сильных электрических полей, делает возможным возникновение МР даже в отсутствие внешнего магнитного поля.
|
|
|
Рис.
11. Зависимость пороговой мощности МР |
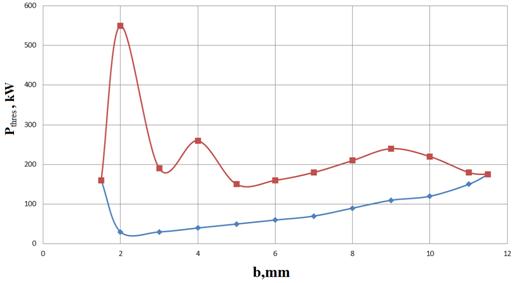
Рассчитанные зависимости нижнего и верхнего порогов МР от
размера b узкой стенки медного волновода
шириной а=72 мм представлены на рис. 12. Существование двухповерхностного разряда
оказывается возможным в диапазоне значений b, лежащих в пределах ![]() мм, т.е.
при соотношении размеров стенок волновода
мм, т.е.
при соотношении размеров стенок волновода ![]() . При
величинах
. При
величинах ![]() мм разряд в области верхней границы имеет
выраженный резонансный характер и может существовать в наиболее широкой области
значений передаваемой мощности Р. При
мм разряд в области верхней границы имеет
выраженный резонансный характер и может существовать в наиболее широкой области
значений передаваемой мощности Р. При ![]() мм углы
пролета между последовательными соударениями с широкими стенками
высокоэнергетической части электронов оказываются меньшими
мм углы
пролета между последовательными соударениями с широкими стенками
высокоэнергетической части электронов оказываются меньшими ![]() , а энергия более медленных электронов –
недостаточной для поддержания процесса умножения числа частиц в разряде. Таким
образом, перестают выполняться и фазовые, и энергетические условия
существования MP, и разряд при соотношении сторон
, а энергия более медленных электронов –
недостаточной для поддержания процесса умножения числа частиц в разряде. Таким
образом, перестают выполняться и фазовые, и энергетические условия
существования MP, и разряд при соотношении сторон ![]() волновода невозможен.
волновода невозможен.
|
|
|
Рис. 12. Зависимости верхней и нижней границ пороговой мощности МР от высоты
b волновода с размером широкой
стенки a = 72 мм |
4. Выводы
В результате исследований, выполненных с помощью разработанной программы SMRW, найдены пороговые уровни мощности СВЧ, приводящие к возникновению мультипакторного разряда в электромагнитном поле волны Н10 прямоугольного волновода. Моделирование МР проведено с учетом свойств материала стенок волновода (бескислородной меди), а также условий пайки, откачки и эксплуатации волновода, соответствующих стандартным требованиям и технологическим процедурам, принятым в производстве мощных электровакуумных приборов СВЧ. Влияние статических магнитных полей на условия возникновения мультипакторного СВЧ разряда рассмотрено с учетом возможных ориентаций вектора магнитной индукции по отношению к волноводу выходного устройства приборов. Найденные величины магнитных полей, способных привести к возникновению МР в волноводе, не выходят за пределы значений, характерных для полей рассеяния фокусирующих магнитных систем мощных ЭВП СВЧ.
Самоподдерживающиеся виды МР в волноводе могут наблюдаться в присутствии магнитных полей, направленных перпендикулярно широким или узким стенкам волновода. В последнем случае разряд имеет резонансный характер и может возникать вблизи частот, кратных удвоенной циклотронной частоте:
![]()
Нерезонансные (полифазные) виды разряда
возможны в широком интервале передаваемых мощностей и величин постоянного магнитного
поля. В медных волноводах при соотношении сторон ![]() возможен
двухповерхностный МР в отсутствие внешнего магнитного поля.
возможен
двухповерхностный МР в отсутствие внешнего магнитного поля.
Полученные результаты указывают на необходимость учета возможности возникновения мультипакторного разряда в волноводах выводов энергии при разработке выходных устройств мощных ЭВП СВЧ и выработки эффективных способов его предотвращения.
Литература
1. Shemelin V.D. Multipactor discharge in a rectangular waveguide with regard to normal and tangential velocity components of secondary electrons // [Электронный ресурс]. URL: http ://www.lns.cornell.edu/public/SRF/2001/SRF010322-03/SRF010322-03.pdf
2. Gusarova M.A., Kaminskii V.I., Kravchuk L.V., Kutsaev S.V., Lalayan M.V, Tarasov S.G., Sobenin N.P. Evolution of 3D Simulation Multipactoring Code MultP // Problems of Atomic Science and Technology. 2008. No. 3. Series: Nuclear Physics Investigations (49). P. 123-126.
3. Geng R.L., Padamsee H.S. Exploring Multipacting Characteristics of a Rectangular Waveguide // Proc. of PAC 1999. New York. USA. P. 429-431.
4. Chojnacki E. Simulation of a Multipactor-Inhibited Waveguide Geometry // [Электронный ресурс]. URL: http://www.lns.cornell.edu/public/SRF/2000/SRF000121-02/SRF000121-02.pdf
5. Geng R.L., Belomestnykh S., Padamsee H., Reilly J., Goudket P., Dykes D.M., Carter R.G. Experimental Studies of Electron Multipacting in CESR Type Rectangular Waveguide Couplers // EPAC 2002. Paris, France. June 3-7 2002. P. 2238.
6. Goniche M., Mhari C. El, Francisquez M., Anza S., Belo J.H., Hertout P., Hillairet J. Modelling of power limit in RF antenna waveguides operated in the lower hybrid range of frequency // Nuclear Fusion. Vol. 54. No. 1. 2014.
7. Baglin V., Bojko J., Gröbner O., Henrist B., Hilleret N., Scheuerlein C., Taborelli M. The secondary electron yield of technical materials and its variation with surface treatments // Proc. of EPAC 2000. Vienna, Austria. P. 217-221.
8. Кулов С.К. Комплексное исследование вторичной электронной эмиссии меди и разработка пленочных антидинатронных покрытий на медной подложке : дис…канд. техн. наук. Москва. МЭИ. 1967.
9. Shigeki Kato, Michiru Nishiwaki. Secondary Electron Emission from Metals and Graphites // Accelerator Technical Design Report for J-PARC. JAERI, KEK. [Электронный ресурс]. URL: http://hadron.kek.jp/~accelerator/TDA/tdr2003/chap2/2.3.8.2.pdf
10. Krienen F. Electron Wind in Strong Wave Guide Fields // IEEE Trans. on Nuclear Science. Vol. NS-32. No. 5. October 1985. P. 2912-2914.
11. Krienen F. X-Radiation from High Power Klystrons. SLAC-PUB-3719. June 1985.
12. Гришин.Л.В., Дорофеюк А.А., Коcсый И.А., Лукьянчиков Г.С., Савченко М.М. Исследование вторично-эмиссионного СВЧ-разряда при больших углах пролета электронов // Труды Физического института им П.Н. Лебедева. 1977. Т. 92. C. 82-131.
13. Прокофьев Б.В. Численное моделирование вторично-электронного разряда на диэлектриках при произвольной ориентации СВЧ-поля // Электронная техника. Сер.1. Электроника СВЧ. 1985. Вып.1(373). С.42-46.
14. Бронштейн И.М., Фрайман Б.С. Вторичная электронная эмиссия // Наука. М. 1969.
15. Gaddy O.L., Holshouser D.F. A microwave frequency cross-field dynamic photomultiplier // Proc. IEEE. January 1963. Vol. 51. P.153-162.
[1] Исследования МР с измерением тока разряда и давления газа в откачанном окнотроне проводились Г.М. Приезжевым и Б.В. Прокофьевым в 1967 г.