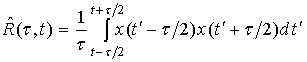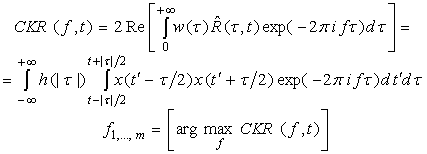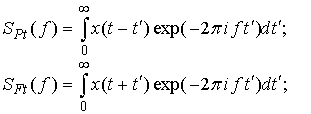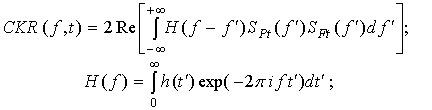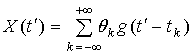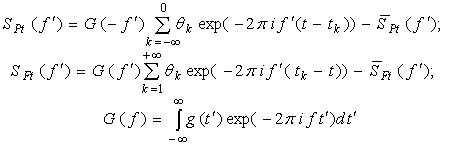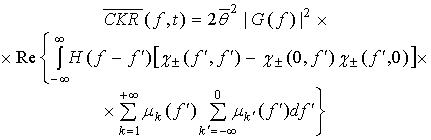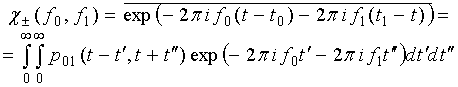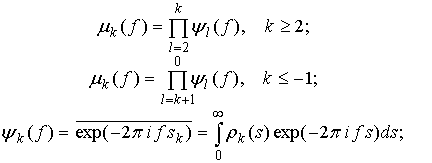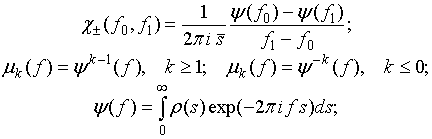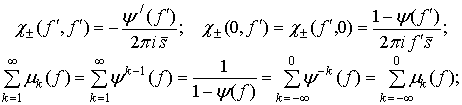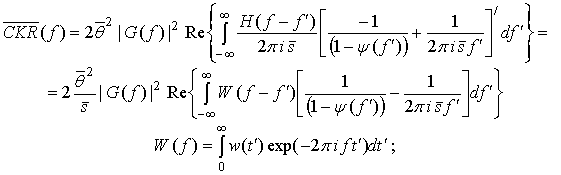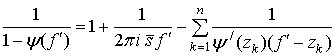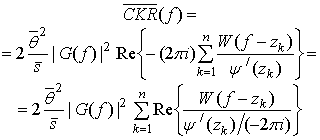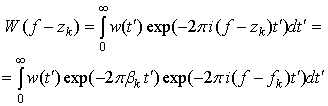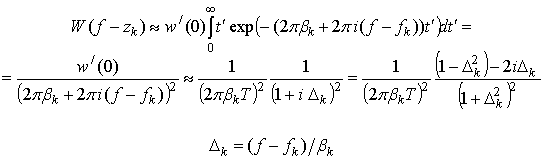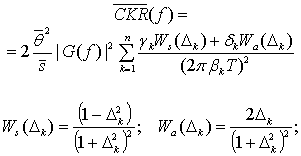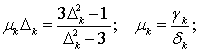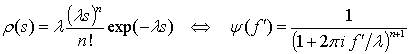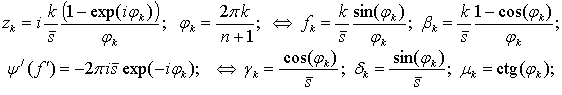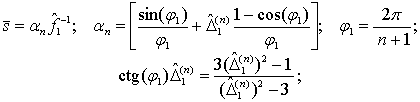УДК 004.93'11
ОЦЕНИВАНИЕ ХАРАКТЕРА ПОСЛЕДЕЙСТВИЯ СЛУЧАЙНЫХ ТОЧЕЧНЫХ ПРОЦЕССОВ МЕТОДАМИ МНОГОМАСШТАБНОГО КОРРЕЛЯЦИОННОГО АНАЛИЗА
В. Е. Анциперов
Институт радиотехники и электроники им. В.А. Котельникова РАН
Статья получена 4 июня 2015 г.
Аннотация. В данной работе обсуждается применение методов многомасштабного корреляционного анализа к проблеме оценивания характеристик широкополосных импульсных процессов с независимыми интервалами между импульсами (точечных процессов с ограниченным последействием). Показано, что для усредненных многомасштабных (конусных) представлений удается, если использовать технику аналитических спектров и, соответственно, методы теории функций комплексного переменного, существенно упростить их вид. Это обстоятельство существенно облегчает анализ зависимости характерных особенностей представлений от параметров потока импульсов. К последним относятся, например, средняя интенсивность, ее вариабельность, характер последействия и т.д. На основе выявленных аналитических зависимостей предложено построение соответствующих оценок по выборочным данным – реализациям импульсных процессов. Среди случаев, в которых удается провести аналитические вычисления до квадратур, рассматриваются случай стационарного потока и случай резкого изменения стационарности. Эти случаи моделируют две крайние ситуации – квазистационарного поведения процесса и переходной режим.
Ключевые слова: точечные процессы, частотно−временной анализ, широкополосные импульсные процессы, многомасштабный корреляционный анализ, аналитические спектры.
Abstract: This paper discusses the application of multiscale correlation analysis to the problem of evaluating the characteristics of wideband pulse processes with independent intervals (point processes with limited aftereffects – renewal processes). It is shown that for the averaged multiscale (cone kernel) representations it is possible, by using the technique of analytic spectra and, accordingly, the methods of the theory of functions of a complex variable, to simplify significantly their appearance. The latter greatly facilitates the dependence of representation characteristics on the process parameters such as average intensity, its variability, character of aftereffects, etc. Basing on the analytical dependences found the paper suggests a construction of the corresponding estimates formed by sampled data – pulse processes realizations. Among the cases in which it is possible to carry out the analytical calculation to the final quadrature the case of a stationary flow and the case of sudden stationarity changes are considered.
Key words: point processes, time−frequency analysis, wideband pulse processes, multiscale correlational analysis, analytic spectra.
Введение
На сегодняшний день средства коммуникации на основе цифровых технологий или уже завоевали лидирующие позиции в большинстве современных областей связи, или находятся в процессе их завоевания. Это обусловлено тем, что цифровая связь по сравнению с аналоговой обеспечивает большую помехозащищенность информации, неограниченные возможности ее структурирования, стандартизации, защиты и т.д. Кроме того, поскольку в состав современных цифровых устройств входят мощные микропроцессоры, интегральные схемы памяти, средства накопления данных и т.д., цифровые технологии способны предоставить огромное количество дополнительных сервисных услуг.
Переход от аналоговых технологий к цифровым явился важным шагом на пути развития современных цифровых телекоммуникационных сетей. Одним из этапов этого процесса стал переход от технологии коммутации каналов передачи данных к коммутации пакетов. В отличие от коммутации каналов, где данные передаются целиком и непрерывно, в сетях с пакетной коммутацией информация передаются дискретными порциями. Такими порциями могут быть пакеты, кадры или ячейки (в зависимости от протокола), но в любом случае они передаются по разделяемой сети. Новые технологии передачи (цифровых) данных потребовали и новых эффективных методов проектирования и анализа соответствующих сетей. Разработка новых методов, в свою очередь, потребовала привлечения новых моделей представления данных и новых подходов в описании связанных с передачей данных процессов [1].
Разработка теории телетрафика для пакетных сетей была в значительной степени осуществлена в 90-х годах прошлого века. Исследуя трафик в реальных сетях, специалисты довольно быстро пришли к выводу о неадекватности модели пуассоновских потоков, ранее широко применявшихся в телефонных сетях (с коммутацией каналов), новым задачам [2]. Основная проблема заключается в том, что с ростом числа запросов пуассоновские потоки имеют тенденцию приобретать черты стационарных процессов с все более сглаженными динамическими характеристиками. Реальные же процессы с ростом трафика наоборот демонстрируют вспышки резкой активности произвольной длительности (см. Рис.1).
В определенном смысле реальный трафик не только не является стационарным, но характеризуется скорее фрактальными свойствами, свойствами самоподобия на разных временных масштабах. Поэтому для его моделирования пришлось обратиться к отнюдь не элементарным разделам математики, статистики и радиофизики. Отметим здесь, например, теорию случайных процессов имеющих распределения с тяжелыми хвостами, с длинно-масштабными корреляциями, мультифрактальностью и т.д. [3]. На Рис.2 приведены наиболее популярные распределения с тяжелыми хвостами, которые чаще всего используются для моделирования интервалов времени между пакетами в реальном интернет–трафике.
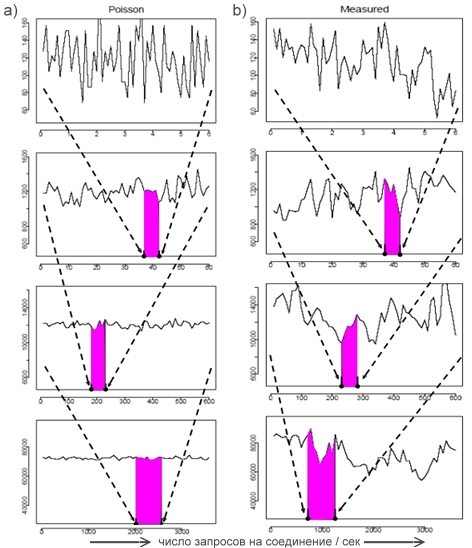
Рис. 1. Сравнение асимптотического поведения
a) смоделированного трафика пуассоновского потока и b) результатов измерения реального интернет–трафика [3].
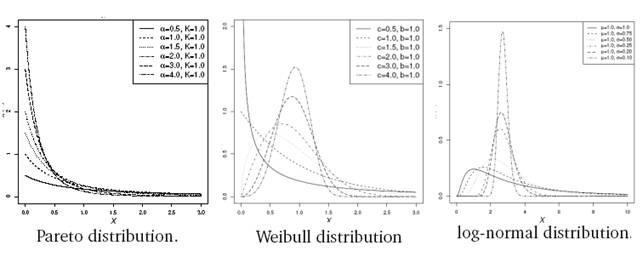
Рис.
2. Популярные распределения (с тяжелыми хвостами) интервалов между событиями
(фрактальных) процессов восстановления, наиболее адекватно моделирующие реальный
интернет–трафик.
В результате усилий специалистов в перечисленных выше областях были развиты различные подходы и методы анализа данных “событийного” типа и описывающих их динамику точечных процессов. Однако, как отмечается в [4], зачастую эти подходы базируются на достаточно сложной математике и требуют понимания достаточно глубоких абстрактных концепций. Последнее затрудняет освоение имеющихся теоретических методов техническим и инженерным персоналом и вынуждает их ограничиваться в большинстве случаев качественным, эмпирическим анализом. При этом следует учесть, что сегодня для решения большинства практических задач проектирования, оптимизации и администрирования современных телекоммуникационных сетей привлекаются в первую очередь инженерные службы. Поэтому актуальной представляется потребность в разработке хотя бы и оценочных, но не выходящих за рамки стандартного технического образования [5] количественных методов анализа сетевых данных и их потоков.
В данной статье мы приводим некоторые достаточно простые методы количественного оценивания параметров нестационарных в целом сигналов. Эти методы основаны на развиваемом нами в течение нескольких последних лет подходе, названном многомасштабным корреляционным анализом (МКА). На практике эти методы использовались для анализа медико–биологических сигналов [6–8] типа последовательностей событий [9] , где они дали весьма удовлетворительные результаты. Эксперименты с реальными сигналами позволили в свою очередь определенным образом скорректировать процедуры оценивания, в частности, была развита тесно связанная с МКА техника аналитических спектров. Применение техники аналитических спектров к имеющим характер точечных процессов сигналам и их моделям также обсуждаются ниже.
Основы МКА формализма
Основы многомасштабного корреляционного анализа (МКА) были
изложены в работе [10]. Главная идея метода состоит в том, что анализ нестационарных
сигналов естественнее основывать на свойствах повторяемости некоторых
сигнальных фрагментов, нежели на свойствах (локальной) аппроксимируемости
сигнала спектром колебательных компонент. Простейшая количественная оценка
повторяемости формируется на основе скалярного произведения совмещенных версий
анализируемых фрагментов. Чем больше величина оценки, тем ближе фрагменты по
форме. Основной технический вопрос состоит в том, как следует выбирать
сравниваемые фрагменты: какой они должны быть длительности, как должны
располагаться по отношению друг к другу и т.д. В МКА для каждого анализируемого
(текущего) момента времени ![]() предлагается выбирать смежные,
примыкающие к этому моменту слева (прошлое) и справа (будущее) фрагменты. При
этом, поскольку период повторяемости заранее не известен, предлагается
формировать оценку повторяемости для всех допустимых длительностей смежных
фрагментов, среди которых, возможно, и присутствует кратная искомому периоду.
Другими словами, длительность фрагментов
предлагается выбирать смежные,
примыкающие к этому моменту слева (прошлое) и справа (будущее) фрагменты. При
этом, поскольку период повторяемости заранее не известен, предлагается
формировать оценку повторяемости для всех допустимых длительностей смежных
фрагментов, среди которых, возможно, и присутствует кратная искомому периоду.
Другими словами, длительность фрагментов ![]() – временной масштаб сравнения – является
переменным, варьируемым параметром метода, что отражено в названии метода
“многомасштабный”. Таким образом, формируемая по методу МКА величина
повторяемости является некоторым двухпараметрическим (с параметрами
– временной масштаб сравнения – является
переменным, варьируемым параметром метода, что отражено в названии метода
“многомасштабный”. Таким образом, формируемая по методу МКА величина
повторяемости является некоторым двухпараметрическим (с параметрами ![]() и
и ![]() ) квадратичным (второй степени по размерности сигнала)
представлением.
) квадратичным (второй степени по размерности сигнала)
представлением.
Формально, если выбрать примыкающие к моменту ![]() слева / справа фрагменты сигнала
слева / справа фрагменты сигнала ![]() длительности
длительности ![]() и сдвинуть их навстречу друг другу на величину
и сдвинуть их навстречу друг другу на величину ![]() до совмещения, то оценку величины повторяемости
до совмещения, то оценку величины повторяемости ![]() можно записать в виде:
можно записать в виде:
где
множитель ![]() перед интегралом введен с целью нормировки. Смысл нормировки состоит в том,
чтобы в квазистационарном случае обеспечить несмещенность
перед интегралом введен с целью нормировки. Смысл нормировки состоит в том,
чтобы в квазистационарном случае обеспечить несмещенность ![]() как оценки автокорреляционной функции сигнала
как оценки автокорреляционной функции сигнала ![]() (в данном случае слабо зависящей от
(в данном случае слабо зависящей от ![]() ) [11].
) [11].
После того, как для некоторого момента времени ![]() оценка (1) сформирована, необходимо выбрать те масштабы
оценка (1) сформирована, необходимо выбрать те масштабы ![]() , на которых повторяемость наиболее выражена. Как отмечено
выше, этим масштабам соответствуют максимумы
, на которых повторяемость наиболее выражена. Как отмечено
выше, этим масштабам соответствуют максимумы ![]() . Однако, в отличие от теоретической
корреляционной функции
. Однако, в отличие от теоретической
корреляционной функции ![]() , у которой все максимумы обусловлены повторяемостью, не
все максимумы эмпирической оценки
, у которой все максимумы обусловлены повторяемостью, не
все максимумы эмпирической оценки ![]() связаны с повторяемостью – часть из
них может быть связана со случайными флуктуациями, помехами, характером
нестационарности и т.д.
связаны с повторяемостью – часть из
них может быть связана со случайными флуктуациями, помехами, характером
нестационарности и т.д.
В результате многочисленных экспериментов было эмпирически
обнаружено, что наиболее устойчивой и надежной процедурой определения связанных
с повторяемостью масштабов ![]() является поиск максимумов не самой
оценки
является поиск максимумов не самой
оценки ![]() , а максимумов
, а максимумов ![]() связанного с ней представления
связанного с ней представления ![]() – аналога оконного (короткого) преобразования Фурье (STFT) [12]:
– аналога оконного (короткого) преобразования Фурье (STFT) [12]:
где ![]() – окно STFT,
– окно STFT, ![]() – ядро преобразования,
– ядро преобразования, ![]() – реальная часть комплексного выражения,
– реальная часть комплексного выражения, ![]() – положения локальных максимумов. Наивное объяснение эффективности (2)
может быть связано с тем, что обусловленные повторяемостью масштабы, как правило,
кратны
– положения локальных максимумов. Наивное объяснение эффективности (2)
может быть связано с тем, что обусловленные повторяемостью масштабы, как правило,
кратны ![]() (масштабы
(масштабы ![]() , как правило, эквидистантны с периодом
, как правило, эквидистантны с периодом ![]() ). Более обоснованное объяснение может быть получено лишь при
более глубоком анализе представления
). Более обоснованное объяснение может быть получено лишь при
более глубоком анализе представления ![]() (2), которому посвящена оставшаяся
часть работы.
(2), которому посвящена оставшаяся
часть работы.
Отметим, что получившееся в результате представление (2) в точности совпадает с введенными в [13] частотно–временными представлениями “конусного” типа (cone kernel representations), детальный анализ свойств которых представлен в [14]. Последнее наблюдение приводит к альтернативной интерпретации оценки (1) и предоставляет в наше распоряжение целый ряд найденных ранее [14] полезных свойств как представления (2), так, в конечном счете, и самой оценки повторяемости (1).
Представление (2) для оценки (1) может быть записано с помощью аналитических спектров, как это было продемонстрировано в работах [6–8]. Локальные аналитические спектры прошлого и будущего определяются следующим образом:
где ![]() является, вообще говоря, комплексной частотой. Отметим, что
аналогично аналитическому сигналу [14] аналитические спектры (3) являются
аналитическими функциями в нижней полуплоскости комплексной плоскости, что и
нашло отражение в названии “ аналитические”. Если формально взять обратное
преобразование Фурье от произведения спектров (3), то результат в случае
является, вообще говоря, комплексной частотой. Отметим, что
аналогично аналитическому сигналу [14] аналитические спектры (3) являются
аналитическими функциями в нижней полуплоскости комплексной плоскости, что и
нашло отражение в названии “ аналитические”. Если формально взять обратное
преобразование Фурье от произведения спектров (3), то результат в случае ![]() в точности совпадет с
в точности совпадет с ![]() (1) и будет тождественно равен нулю в
случае
(1) и будет тождественно равен нулю в
случае ![]() . Этого достаточно, чтобы переписать (2) в виде:
. Этого достаточно, чтобы переписать (2) в виде:
МКА в случае точечных процессов
Дальнейшее уточнение особенностей выявления повторяемости на
основе оценок (2), (4) предполагает привлечение дополнительной информации о
сигнале ![]() . Так, например, в [6] приведены свойства представлений (4) для
“узкополосных” компонент ЭЭГ сигналов, типа компонент
. Так, например, в [6] приведены свойства представлений (4) для
“узкополосных” компонент ЭЭГ сигналов, типа компонент ![]() – ритма и др. В данной работе ниже обсуждаются
результаты исследований соответствующих свойств для (широкополосных) сигналов
импульсного вида:
– ритма и др. В данной работе ниже обсуждаются
результаты исследований соответствующих свойств для (широкополосных) сигналов
импульсного вида:
где ![]() случайные моменты времени появления импульсов,
случайные моменты времени появления импульсов, ![]() − соответствующий набор случайных амплитуд и
− соответствующий набор случайных амплитуд и ![]() – неслучайная форма отдельного импульса. Для технических целей, однако,
удобнее пользоваться не самим сигналом (5), а его центрированной версией
– неслучайная форма отдельного импульса. Для технических целей, однако,
удобнее пользоваться не самим сигналом (5), а его центрированной версией ![]() , где
, где ![]() − медленная составляющая, среднее процесса, связанное
с интенсивностью точечного потока моментов импульсов сигнала
− медленная составляющая, среднее процесса, связанное
с интенсивностью точечного потока моментов импульсов сигнала ![]() . Подобная процедура центрирования, фильтрации процесса
практически всегда предполагается при анализе квадратичных представлений типа
(2).
. Подобная процедура центрирования, фильтрации процесса
практически всегда предполагается при анализе квадратичных представлений типа
(2).
В случае слабого перекрытия импульсов,
когда выполняется соотношение ![]() , где
, где ![]() − длительность импульса, а
− длительность импульса, а ![]() − средний период следования импульсов, сигнал (5) близок к
идеальному точечному процессу и выражения (3) для аналитических спектров можно
упростить до следующего вида:
− средний период следования импульсов, сигнал (5) близок к
идеальному точечному процессу и выражения (3) для аналитических спектров можно
упростить до следующего вида:
где ![]() и
и ![]() − аналитические спектры (3) среднего
− аналитические спектры (3) среднего ![]() .
.
Линейная зависимость аналитических спектров (6) от случайных
параметров ![]() и показательная
от
и показательная
от ![]() теоретически позволяет найти максимально полное
статистическое описание
теоретически позволяет найти максимально полное
статистическое описание ![]() (4), если пересчитать статистику совокупности
случайных параметров
(4), если пересчитать статистику совокупности
случайных параметров ![]() и
и ![]() в статистическое распределение представления. Практически,
однако, за исключением нескольких модельных ситуаций, этого сделать не удается.
Поэтому примем следующие упрощающие предположения. Будем считать, что
случайные амплитуды
в статистическое распределение представления. Практически,
однако, за исключением нескольких модельных ситуаций, этого сделать не удается.
Поэтому примем следующие упрощающие предположения. Будем считать, что
случайные амплитуды ![]() имеют одинаковые средние
имеют одинаковые средние ![]() и статистически независимы в
совокупности. Будем считать их также независимыми от последовательности
моментов
и статистически независимы в
совокупности. Будем считать их также независимыми от последовательности
моментов ![]() . Для случайных же моментов
. Для случайных же моментов ![]() выберем модель точечного потока с
ограниченным последействием [15]. Последнее означает по существу, что интервалы
выберем модель точечного потока с
ограниченным последействием [15]. Последнее означает по существу, что интервалы
![]() между импульсами независимы в совокупности (но, вообще
говоря, распределены не одинаково – каждый интервал имеет свое распределение
между импульсами независимы в совокупности (но, вообще
говоря, распределены не одинаково – каждый интервал имеет свое распределение ![]() ) и, соответственно, независимы от предыстории процесса
) и, соответственно, независимы от предыстории процесса ![]() . Однако и в представленной упрощенной модели найти
распределение представления
. Однако и в представленной упрощенной модели найти
распределение представления ![]() (4) все еще сложно. Ввиду отмеченных
трудностей можно для полуколичественного анализа представления ограничиться его
сжатым статистическим описанием при помощи математического ожидания (среднего)
(4) все еще сложно. Ввиду отмеченных
трудностей можно для полуколичественного анализа представления ограничиться его
сжатым статистическим описанием при помощи математического ожидания (среднего) ![]() , а само представление, полученное на основе выборочных реализаций
рассматривать (на основе, например, статистического закона больших чисел) как
некоторое приближение к среднему.
, а само представление, полученное на основе выборочных реализаций
рассматривать (на основе, например, статистического закона больших чисел) как
некоторое приближение к среднему.
После ряда вычислений и на основе принятых допущений (включая (6)) среднее от (4) может быть представлено в виде:
где ![]() и
и ![]() − диагональный и граничные элементы характеристической
функции двумерного распределения
− диагональный и граничные элементы характеристической
функции двумерного распределения ![]() моментов непосредственно предшествующего и
непосредственно следующего за текущим моментом
моментов непосредственно предшествующего и
непосредственно следующего за текущим моментом ![]() (
(![]() ):
):
а элементы
совокупностей ![]() (за исключением
(за исключением ![]() ) выражаются через характеристические функции распределений
) выражаются через характеристические функции распределений
![]() в виде:
в виде:
Важнейшей особенностью ![]() (7) является то, что она тождественно
обращается в нуль при независимых
(7) является то, что она тождественно
обращается в нуль при независимых ![]() , т.е. при
, т.е. при ![]() (
( ![]() ). Ввиду приведенной выше аргументации аналогичным свойством
будет обладать и представление (4): если будущее сигнала
). Ввиду приведенной выше аргументации аналогичным свойством
будет обладать и представление (4): если будущее сигнала ![]() , начиная с момента
, начиная с момента ![]() ,
статистически не
зависит от прошлого, представление
,
статистически не
зависит от прошлого, представление ![]() редуцируется к шумовому. Последнее,
в частности, относится к пуассоновскому процессу, так как при фиксированном
моменте времени
редуцируется к шумовому. Последнее,
в частности, относится к пуассоновскому процессу, так как при фиксированном
моменте времени ![]() моменты
моменты ![]() и
и ![]() (прямое и обратное времена
возвращения) независимы [15], что, собственно, и подразумевается термином “процесс
без последействия”.
(прямое и обратное времена
возвращения) независимы [15], что, собственно, и подразумевается термином “процесс
без последействия”.
МКА в случае стационарных точечных процессов (Пальма / Эрланга)
Для того, чтобы проанализировать вид ![]() в противоположной ситуации – зависимых
в противоположной ситуации – зависимых ![]() (при наличии последействия), полезно рассмотреть
другой крайний случай − когда моменты
(при наличии последействия), полезно рассмотреть
другой крайний случай − когда моменты ![]() являются потоком Пальма (хотя бы и
на ограниченном интервале квазистационарности). Последний является стационарным
точечным потоком с ограниченным последействием, у которого распределения
интервалов
являются потоком Пальма (хотя бы и
на ограниченном интервале квазистационарности). Последний является стационарным
точечным потоком с ограниченным последействием, у которого распределения
интервалов ![]() между импульсами одинаковы:
между импульсами одинаковы: ![]() [15]. В этом случае
[15]. В этом случае ![]() , где
, где ![]() – среднее значение
длительности каждого из интервалов по общему распределению с плотностью
– среднее значение
длительности каждого из интервалов по общему распределению с плотностью ![]() . Для данной модели процесса двумерная характеристическая
функция
. Для данной модели процесса двумерная характеристическая
функция ![]() (8) и
совокупность
(8) и
совокупность ![]() (9) могут
быть найдены явно:
(9) могут
быть найдены явно:
С учетом (10) явно же находятся и входящие в (7) подынтегральные сомножители:
Заметим, что все сомножители (11), также, как и определяемый
ими интеграл, и, в конечном счете, ![]() не зависят от текущего времени
не зависят от текущего времени ![]() . Это является естественным следствием (квази)
стационарности рассматриваемого процесса. С учетом данного замечания и с целью
подчеркнуть стационарность анализируемой ситуации будем далее опускать время
. Это является естественным следствием (квази)
стационарности рассматриваемого процесса. С учетом данного замечания и с целью
подчеркнуть стационарность анализируемой ситуации будем далее опускать время ![]() у усредненного представления (7) и
записывать его как
у усредненного представления (7) и
записывать его как ![]() .
.
Подставляя (11) в (7), после однократного интегрирования по частям окончательно получим:
где учтена связь
спектров ![]() и
и ![]() :
: ![]() .
.
Отметим, что в силу определения (10), характеристическая
функция ![]() ограничена по модулю единицей
ограничена по модулю единицей ![]() .
Последнее выполняется в виде
строгого неравенства во всей открытой нижней полуплоскости комплексного
переменного, если допустить для
.
Последнее выполняется в виде
строгого неравенства во всей открытой нижней полуплоскости комплексного
переменного, если допустить для ![]() комплексные значения. Из этого
следует, что все особенности подынтегрального выражения в квадратных скобках в (12)
могут лежать только в верхней комплексной полуплоскости. При этом, заметим, нуль
не является особенностью, так как при малых
комплексные значения. Из этого
следует, что все особенности подынтегрального выражения в квадратных скобках в (12)
могут лежать только в верхней комплексной полуплоскости. При этом, заметим, нуль
не является особенностью, так как при малых ![]() имеет место
имеет место ![]() , и слагаемые в квадратных скобках компенсируются.
, и слагаемые в квадратных скобках компенсируются.
Сомножитель ![]() , наоборот, в верхней полуплоскости не имеет особенностей,
являясь там аналитической функцией. Это вытекает из определения (12) в силу
которого спектр
, наоборот, в верхней полуплоскости не имеет особенностей,
являясь там аналитической функцией. Это вытекает из определения (12) в силу
которого спектр ![]() аналитичен в нижней полуплоскости. Отсюда следует, что все особенности в
подынтегральном выражении для
аналитичен в нижней полуплоскости. Отсюда следует, что все особенности в
подынтегральном выражении для ![]() (12), находящиеся в верхней
полуплоскости, связаны только с характеристической функцией
(12), находящиеся в верхней
полуплоскости, связаны только с характеристической функцией ![]() . Их расположения задаются корнями уравнения
. Их расположения задаются корнями уравнения ![]() (исключая корень
(исключая корень ![]() ). В
ряде случаев знания этих корней оказывается достаточно для вычисления самого
интеграла.
). В
ряде случаев знания этих корней оказывается достаточно для вычисления самого
интеграла.
Таким случаем является случай дробно–рациональных ![]() . Выражение в квадратных скобках под интегралом в (12) будет при этом
также дробно–рациональным и поэтому может быть разложено на сумму простейших
дробей. Интегралы же от простейших дробей вместе с аналитическим спектром
. Выражение в квадратных скобках под интегралом в (12) будет при этом
также дробно–рациональным и поэтому может быть разложено на сумму простейших
дробей. Интегралы же от простейших дробей вместе с аналитическим спектром ![]() могут быть вычислены с помощью теории вычетов.
могут быть вычислены с помощью теории вычетов.
Проиллюстрируем этот случай в ситуации, когда уравнение ![]() имеет
имеет ![]() корней (включая нулевой) и все они являются
простыми:
корней (включая нулевой) и все они являются
простыми:
где учтено,
что, во–первых, на бесконечности ![]() и поэтому в качестве постоянного
члена разложения в (13) фигурирует единица, а, во–вторых, что для выделенной в
отдельное слагаемое дроби, соответствующей корню
и поэтому в качестве постоянного
члена разложения в (13) фигурирует единица, а, во–вторых, что для выделенной в
отдельное слагаемое дроби, соответствующей корню ![]() ,
производная
,
производная ![]() равна
равна ![]() . Последнее слагаемое в (13) соответствует суммированию по
оставшимся
. Последнее слагаемое в (13) соответствует суммированию по
оставшимся ![]() ненулевым корням
ненулевым корням ![]() . Отметим, что в силу симметрии
. Отметим, что в силу симметрии ![]() все эти корни расположены симметрично относительно мнимой оси. В общем
случае среди них будет
все эти корни расположены симметрично относительно мнимой оси. В общем
случае среди них будет ![]() пар корней вида
пар корней вида ![]() с
с ![]() и
и ![]() чисто мнимых ненулевых корней при
чисто мнимых ненулевых корней при ![]() .
.
Если замкнуть контур интегрирования в (12) в верхней
полуплоскости и воспользоваться разложением (13), то с помощью теории вычетов сразу
же получается следующее представление ![]() :
:
где учтено,
что интеграл от ![]() с единицей дает
с единицей дает ![]() , а слагаемое
, а слагаемое ![]() в разложении (13) сокращается с
соответствующим членом в интеграле, как это отмечалось выше.
в разложении (13) сокращается с
соответствующим членом в интеграле, как это отмечалось выше.
С целью упростить анализ полученного выражения (14) для ![]() , рассмотрим, исходя из определения (12), входящие в (14) величины
сдвинутых спектров
, рассмотрим, исходя из определения (12), входящие в (14) величины
сдвинутых спектров ![]() ,
, ![]() :
:
В (15)
показатели действительных экспонент ![]() имеют порядок величин ~
имеют порядок величин ~![]() . Если длительность
. Если длительность
![]() окна
окна ![]() существенно превосходит среднюю длительность интервалов
существенно превосходит среднюю длительность интервалов ![]() так, что
так, что ![]() , то интеграл (15) может быть вычислен приближенно методом
Лапласа (с учетом
, то интеграл (15) может быть вычислен приближенно методом
Лапласа (с учетом ![]() ):
):
где принято,
что производная в нуле ![]() имеет порядок ~
имеет порядок ~![]() . Вводя обозначения
. Вводя обозначения ![]() и
и ![]() для действительной и мнимой частей
выражения
для действительной и мнимой частей
выражения ![]() , запишем с учетом (16) приближенную версию (14):
, запишем с учетом (16) приближенную версию (14):
Из (17) вытекает, что усредненное представление ![]() имеет следующую
структуру. Оно является суммой
имеет следующую
структуру. Оно является суммой ![]() , возможно, перекрывающихся комплексов
ширины ~
, возможно, перекрывающихся комплексов
ширины ~![]() , центры которых расположены в точках
, центры которых расположены в точках ![]() . Каждый из комплексов является помноженной на весовой
коэффициент
. Каждый из комплексов является помноженной на весовой
коэффициент ![]() линейной комбинацией симметричной
линейной комбинацией симметричной ![]() и антисимметричной
и антисимметричной ![]() составляющих, где
составляющих, где ![]() . Коэффициенты соответствующих линейных комбинаций
. Коэффициенты соответствующих линейных комбинаций ![]() и
и ![]() – действительная и мнимая части
– действительная и мнимая части ![]() .
.
Отметим, что из–за антисимметричной составляющей ![]() положение
положение ![]() каждого из комплексов не совпадает с
положением его максимума (исключая случай чисто мнимых корней с
каждого из комплексов не совпадает с
положением его максимума (исключая случай чисто мнимых корней с ![]() , для которых
, для которых ![]() ). Обозначая последний посредством
). Обозначая последний посредством ![]() , можно, дифференцируя линейную комбинацию
, можно, дифференцируя линейную комбинацию ![]() , получить следующее поправочное соотношение
связывающее положение центра
, получить следующее поправочное соотношение
связывающее положение центра ![]() –го комплекса
–го комплекса ![]() и положение его максимума
и положение его максимума ![]() :
: ![]() , где
, где ![]() есть то из решений кубического уравнения:
есть то из решений кубического уравнения:
которое положительно
при ![]() и отрицательно в противном случае.
и отрицательно в противном случае.
Если для некоторого процесса ряд комплексов в представлении ![]() (17) слабо искажен остальными – незначительно перекрываются с теми, которые
имеют сравнимый или больший вес
(17) слабо искажен остальными – незначительно перекрываются с теми, которые
имеют сравнимый или больший вес ![]() , то на основе
изложенных выше приближений можно предложить следующую процедуру оценивания
параметров повторяемости процесса. Считая параметры повторяемости (неизвестными)
параметрами распределения
, то на основе
изложенных выше приближений можно предложить следующую процедуру оценивания
параметров повторяемости процесса. Считая параметры повторяемости (неизвестными)
параметрами распределения ![]() , выразим через них для разделяемых
комплексов (с номерами
, выразим через них для разделяемых
комплексов (с номерами ![]() ) величины
) величины ![]() и найдем
и найдем ![]() (18). Затем, определяя по полученному на
основе выборочных реализаций представлению
(18). Затем, определяя по полученному на
основе выборочных реализаций представлению ![]() (4) максимумы
(4) максимумы ![]() соответствующих комплексов, свяжем с ними параметры повторяемости при
помощи поправочных соотношений
соответствующих комплексов, свяжем с ними параметры повторяемости при
помощи поправочных соотношений ![]() . Разрешая последние уравнения
относительно параметров повторяемости, получим тем самым для них
скорректированные оценки через максимумы
. Разрешая последние уравнения
относительно параметров повторяемости, получим тем самым для них
скорректированные оценки через максимумы ![]() .
.
Описанную выше процедуру оценки параметров для общих
процессов Пальма, конкретизируем для важного в приложениях частного случая
процессов Эрланга. Для процессов Эрланга плотность распределения ![]() и, соответственно, ее характеристическая функция
и, соответственно, ее характеристическая функция ![]() (10) имеют следующий явный вид [15]:
(10) имеют следующий явный вид [15]:
где ![]() – целое, порядок распределения, а
– целое, порядок распределения, а ![]() – его параметр. В крайнем случае
– его параметр. В крайнем случае ![]() получается не представляющий интереса
в данном случае пуассоновский процесс (без последействия), поэтому далее
предполагается
получается не представляющий интереса
в данном случае пуассоновский процесс (без последействия), поэтому далее
предполагается ![]() .
.
Для процессов Эрланга среднее значение длительности интервалов между импульсами ![]() очень просто связано с порядком и
параметром распределения:
очень просто связано с порядком и
параметром распределения: ![]() . Отсюда, рассматривая
. Отсюда, рассматривая
![]() как параметр повторяемости процесса,
легко перепараметризировать
как параметр повторяемости процесса,
легко перепараметризировать ![]() посредством замены параметра
посредством замены параметра ![]() . В итоге,
. В итоге, ![]() корней
уравнения
корней
уравнения ![]() , значения производной
, значения производной ![]() в этих корнях и, соответственно, значения
в этих корнях и, соответственно, значения
![]() могут быть найдены явно и имеют вид:
могут быть найдены явно и имеют вид:
Из (20) следует, что веса ![]() комплексов
на положительной полуоси (
комплексов
на положительной полуоси (![]() от единицы до ~
от единицы до ~ ![]() ) убывают с ростом их номера как ~
) убывают с ростом их номера как ~ ![]() . Это означает, что для оценки
. Это означает, что для оценки ![]() наиболее подходящим будет максимум
первого комплекса, он же первый боковой максимум
наиболее подходящим будет максимум
первого комплекса, он же первый боковой максимум ![]() . В этом случае (
. В этом случае (![]() ) поправочное соотношение, связывающее
положение первого максимума
) поправочное соотношение, связывающее
положение первого максимума ![]() с оценкой
с оценкой ![]() будет
иметь вид:
будет
иметь вид:
Для каждого порядка ![]() входящая в поправочный коэффициент
входящая в поправочный коэффициент ![]() величина
величина ![]() является зависящей только от
является зависящей только от ![]() константой и рассчитывается на основе
последнего соотношения в (21). Для небольших значений
константой и рассчитывается на основе
последнего соотношения в (21). Для небольших значений ![]() можно
можно ![]() и
и ![]() можно вычислить непосредственно, для больших
можно вычислить непосредственно, для больших ![]() имеет место следующая асимптотика:
имеет место следующая асимптотика: ![]() и
и 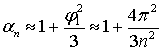 . Интересно, что полученная асимптотика практически совпадает с
соответствующими результатами [16], полученными на основе сильно отличающегося
подхода.
. Интересно, что полученная асимптотика практически совпадает с
соответствующими результатами [16], полученными на основе сильно отличающегося
подхода.
Резюмируя приведенный выше анализ можно заключить, что
определение параметров повторяемости импульсных процессов по максимумам
представления ![]() в высокой степени обосновано. В случае возможной локальной
аппроксимации потоком Эрланга положение первого максимума с небольшой,
зависящей от порядка процесса поправкой, дает хорошую оценку
в высокой степени обосновано. В случае возможной локальной
аппроксимации потоком Эрланга положение первого максимума с небольшой,
зависящей от порядка процесса поправкой, дает хорошую оценку ![]() . В случае нарушения (квази)
стационарности максимумы в представлении
. В случае нарушения (квази)
стационарности максимумы в представлении ![]() исчезают, что также является хорошим
маркером соответствующего режима.
исчезают, что также является хорошим
маркером соответствующего режима.
В целом, можно выразить надежду, что изложенные методы и их развитие найдут широкое применение в практике обработки широкополосных импульсных процессов , включая процессы теле трафика в современных сетях.
Работа выполнена при финансовой поддержке гранта РФФИ N 15-07-04378 -а.
Литература
1. Chen T.M. Network Traffic Modeling. // Handbook of Computer Networks: Distributed Networks, Network Planning, Control, Management, and New Trends and Applications. Ed. by Hossein Bidgoli. John Wiley & Sons, Inc., Hoboken, New Jersey. V.3. 2008.
2. Paxson V. and Floyd S. Wide-area traffic: the failure of Poisson modeling. // IEEE/ACM Transactions on Networking, V.3, N.3, 1995, pp. 226–244.
3. Willinger W. and Paxson V. Where Mathematics meets the Internet. //Notices of the American Mathematical Society, V.45, N.8, 1998, pp. 961-970.
4. Zheng L. and Gallager К. Principles of Digital Communications I, Fall 2006. // Massachusetts Institute of Technology: MIT OpenCourseWare 6.450, эл.ресурс: http://ocw.mit.edu, accessed 6 Apr, 2015.
5. Тихонов В.И. Статистическая радиотехника. Изд. 2-е. // М. : Радио и связь, 1982.
6. Анциперов В.Е. Обнаружение ритмов головного мозга человека на основе корреляции аналитических спектров ЭЭГ в основных диапазонах частот. // Журнал радиоэлектроники, Москва: ИРЭ им. В. А. Котельникова РАН, электронный журнал http://jre.cplire.ru/jre/may14/13/text.pdf, ISSN 1684-1719, N 5 - май 2014 г., всего 11 стр.
7. Анциперов В.Е., Зернов В.А., Растягаев Д.В. Использование техники аналитических спектров для задач автоматизации мониторинга сердечного ритма. // Успехи современной радиоэлектроники, №8, 2014 г., с. 28-36.
8. Анциперов В.Е., Мансуров Г.К. Использование концепции аналитического спектра в задачах мониторинга ритма артериального давления // Доклады VIII Всероссийской научно-технической конференции “Радиолокация и радиосвязь” 24 – 26 ноября 2014 г., Москва, сс. 363-367.
9. Рангаяйн Р.М. Анализ биомедицинских сигналов. Практический подход. // М. : Физматлит, 2010.
10. Анциперов В.Е. Многомасштабный корреляционный анализ нестационарных, содержащих квазипериодические участки сигналов // “Радиотехника и электроника”, т. 53, № 1, 2008 г. стр.73-85.
11. Анциперов В.Е. Новый метод оценки корреляционных функций в задачах обнаружения и обработки радиолокационных и связных сигналов // Доклады III Всероссийской конференции “Радиолокация и радиосвязь”, Москва, 26-30 октября 2009 г, стр. 887-881
12. Time-frequency analysis: concepts and methods. Edited by F. Hlawatsch and F. Auger. // GB and US: ISTE Ltd and John Wiley & Sons, Inc., 2008.
13. Zhao Y., Atlas L. E. and Marks R. J. The use of cone-shape kernels for generalized time-frequency representations of nonstationary signals. // IEEE Trans. Acoustics, Speech, Signal Processing, V. 38, N 7, 1990, pp. 1084–1091.
14. Hlawatsch F., et al. Smoothed pseudo-Wigner distribution, Choi-Williams distribution, and cone-kernel representation: Ambiguity-domain analysis and experimental comparison. // Signal Processing, vol. 43, p. 149-168, 1995.
15. Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения. 2-е изд. // М.: Высшая школа, 2000.
16. Рытов, С.М. Введение в статистическую радиофизику: Случайные процессы. //М: Наука; 1976.