Получена 9 марта 2000 г.

В последнее время в ряде вопросов физики и техники выдвинулся новый класс задач, связанных с нелинейными явлениями при распространении волн в неоднородных средах. Такие задачи возникли в связи с развитием систем генерации, распространения и обработки сверхширокополосного и высокомощного излучения и использованием этого излучения в радиолокации и дистанционном зондировании [1]. Дело в том, что при взаимодействии высокомощного излучения практически с любой средой становятся существенными нелинейные эффекты в этой среде. Вследствие этого рассеянное такой средой излучение будет иметь в своем составе дополнительные спектральные составляющие, которые необходимо учитывать. Существуют также некоторые практически важные среды, которые проявляют нелинейные свойства и при достаточно малых значениях напряженности поля. Среди них особое значение для исследования имеют биологические ткани. В частности, было установлено [2], что на низких частотах вольтамперная характеристика клеточной мембраны очень похожа на характеристики диодов на p-n переходах. Определение нелинейных свойств биологических тканей открывает возможности для более ранней и точной диагностики самых различных заболеваний.

Несмотря на перспективность таких задач, существующие методы анализа рассеяния электромагнитного поля радиодиапазона в нелинейной среде развиты слабо и в основном ограничиваются случаями вибраторных антенн с нелинейной нагрузкой [2-4] или случаем нелинейного контакта двух бесконечных полуплоскостей [5]. Прямой перенос известных методов нелинейной оптики на радиодиапазон не представляется возможным. В настоящее время в радиофизике используются приближенные методы, основанные на расчете характеристик поля вблизи выделенных гармоник на основе применения теории возмущений. Общим недостатком таких методов является то, что они не позволяют наглядно проследить изменение характеристик рассеянного сигнала в зависимости от изменения параметров рассеивающих элементов, параметров нелинейностей и спектральных характеристик падающего излучения.. Для определения полного спектрального состава рассеянного сверхширокополосного излучения необходимо более точно описать процессы в нелинейной среде. Для этого необходимо исходить из общей электродинамической постановки задачи.

В данной работе на основе развития известных аналитических и численных методов предлагается описание рассеянного в нелинейной среде поля в рамках скалярной электродинамической теории. Полученное интегральное уравнение учитывает как пространственные, так и временные изменения исходного сигнала при прохождении через нелинейную среду. Решение рассматривается для достаточно произвольной формы падающей волны и допускает эффективное использование для диагностики вида нелинейности. Показаны условия, при которых полученное уравнение переходит к представлению, используемому в методе эквивалентных схем. В такой постановке задача ранее в научной литературе не ставилась.

Запишем материальные уравнения для нелинейной среды. Для простоты магнитные свойства среды учитывать не будем, считая магнитную проницаемость постоянной. Если среда не изменяет со временем своих свойств, то диэлектрическая проницаемость и проводимость должны зависеть лишь от разности времени. При этом материальные уравнения для векторов электрической индукции и плотности тока в спектральной области принимают вид [6]

 Здесь и - абсолютная диэлектрическая проницаемость и удельная проводимость фоновой среды, которая предполагается линейной и однородной. Вторые слагаемые в квадратных скобках для диэлектрической проницаемости и удельной проводимости связаны с нелинейными возмущениями фоновой среды и зависят от напряженности поля E:

где - функция Грина, - волновое число для фоновой среды. Поле представляет собой напряженность поля первичной волны, а интеграл в правой части описывает рассеянное нелинейными неоднородностями поле. Уравнение (2) записано в скалярном представлении и известно в литературе как уравнение Липпмана-Швингера. Оно получается из дифференциального уравнения Гельмгольца с использованием метода функций Грина.

Важно подчеркнуть, что записанное уравнение (2) представляет собой нелинейное интегральное уравнение. Нелинейность проявляется через зависимость электрофизических параметров среды от напряженности поля. 

Исследуем полученную зависимость для случая, когда неоднородность изолирована и сосредоточена в некоторой точке пространства . Для определенности будем считать, что форма неоднородности аппроксимируется цилиндром длиной и радиусом (рис. 1).

Рис. 1. Элементарная неоднородность

Согласно (2) рассеянное неоднородностью поле и его спектр определяются значениями полного поля в точке расположения неоднородности . Нахождение величины поля составляет так называемую внутреннюю электродинамическую задачу. Для определения его совместим точку наблюдения с центром неоднородности. Оценим интеграл в уравнении (2) в предположении, что характерные размеры неоднородности малы (), и экспоненциальный член под интегралом разложим в ряд по степеням малости ее показателя. В этом случае для внутренней задачи можно записать

Рис. 2. Эквивалентная схема

Здесь введены обозначения, имеющие следующий физический смысл: - электродвижущая сила (ЭДС), наведенная падающим излучением на неоднородности, и - падение напряжения и ток проводимости, наведенные на нелинейном элементе, - эквивалентная емкость. Кроме того, - комплексное входное сопротивление, зависящее от геометрических размеров объекта. Реальная часть c точностью до постоянного множителя совпадает с сопротивлением излучения элементарного вибратора, а мнимая часть соответствует реактивной части входного сопротивления в электродинамике излучающих систем. В случае мнимая часть соответствует индуктивному сопротивлению тонкого провода [7]. Уравнению (4) соответствует эквивалентная схема, изображенная на рис. 2. Такой эквивалентной схемой обычно пользуются в нелинейной радиолокации при описании рассеяния волн нелинейными устройствами [2]. Этим представлением пользуются при анализе реакции вибратора, нагруженного на нелинейность типа нелинейный контакт или диод. В отличие от традиционного подхода уравнение (4) получено нами не из феноменологических соображений, а на основе асимптотического анализа точных волновых представлений.

В общем случае нелинейные свойства среды учтены в уравнении (4) через ток и емкость . Такое представление вида нелинейности элемента через его вольтамперную и вольтфарадную характеристики во временном представлении является общепринятым для практических расчетов [2]. Однако при малых размерах неоднородности нелинейностью емкости можно пренебречь.

С учетом сказанного ясно, что простое по форме уравнение (4) на самом деле является неоднородным нелинейным интегральным уравнением. При произвольном виде вольтамперной характеристики аналитического решения этого уравнение получить не удается. Известны попытки решения этого уравнения методом малых возмущений для слабых нелинейностей. Таким путем оценивалась, например, эффективная поверхность рассеяния нелинейности на гармониках в задачах нелинейной радиолокации [2]. Для решения в более общем случае обычно используется разложение в ряд Вольтерра или численные итерационные методы.

Заметим, что уравнение (4) в общем случае не может быть сведено к явному уравнению для неизвестной функции u как функции от входной переменной ни во временном, ни в частотном представлении. Дело в том, что спектральные изменения результирующего тока и напряжения обусловлены многократным нелинейным преобразованием сигналов во временном представлении. Для анализа этих изменений необходимо совместное использование частотного и временного представлений.

Рассеянное нелинейностью поле полностью определяется полем на ней, что и составляет внешнюю электродинамическую задачу. Согласно (2) поле, рассеянное элементарной неоднородностью, в дальней зоне (при ) можно определить по формуле

где и - амплитуда и центральная частота падающего излучения. Такое представление позволяет выбором параметра моделировать как узкополосные, так и широкополосные сигналы.

Результаты исследования влияния нелинейности на рассеяние сверхширокополосного излучения представлены на рис. 3. Здесь показаны нормированные спектры амплитуд падающей волны (штриховая линия), и волны, рассеянной нелинейным элементом (сплошная линия). На рис. 3а изображены зависимости для нелинейности с вольтамперной характеристикой , соответствующей туннельному контакту, где =18,3 мА/В, а =3,7 мА/В3 [2]. На рис.3б приведены соответствующие характеристики для нелинейности, описывающей мембрану биологической клетки аксона кальмара , где =35 мА, =4,4 мВ [2]. Видно, что при взаимодействии излучения с нелинейной средой происходит образование в спектре рассеянного излучения дополнительных спектральных компонент. Кроме того, в сторону больших частот смещается максимум главной части спектра. Это физически ожидаемые эффекты.

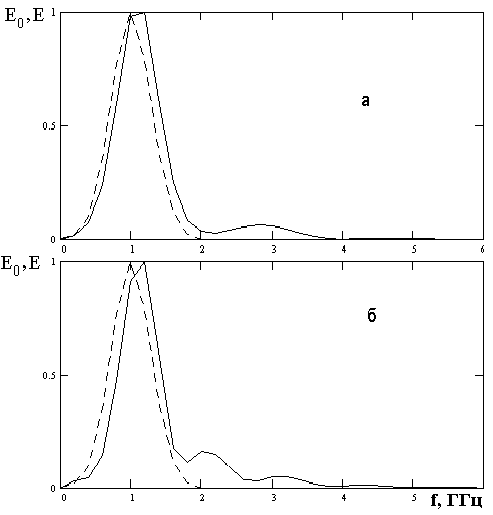
Рис. 3. Нормированные спектры падающей и рассеянной волн

 При использовании импульсного излучения, характеризующегося широкой полосой частот, возможно существенное сужение импульса при распространении излучения в нелинейной среде. Это открывает большие перспективы для создания систем генерации сверхкоротких импульсов. В то же время при высокомощном излучении, начинающем находить применение в современной технике, становятся значительными нелинейные эффекты при взаимодействии излучения со средой, которые нельзя не учитывать. Соответственно встает задача определения нелинейных свойств различных сред для точного нахождения поля в точке приема. В связи с этим назрела необходимость решения задач диагностики нелинейных сред.

Для восстановления вольтамперной характеристики определим ток , протекающий через нелинейный элемент, и падающее на нем напряжение . Они находятся в спектральном представлении как

где определяется по данным падающего поля из соотношения . Далее необходимо перейти во временное представление с использованием обратного Фурье. Искомая вольтамперная характеристика восстанавливается как параметрическая зависимость найденных значений тока от значений напряжения при различных моментах времени.

Рис. 4. Заданные и восстановленные характеристики нелинейностей

Важно отметить, что полное восстановление вида нелинейности требует достаточно большого диапазона изменения используемых токов и напряжений. При использовании постоянных или квазигармонических сигналов это способно привести нелинейный элемент к разрушению. При использовании же сверширокополосного излучения с малой длительностью ( 1 нс) разрушения не будет происходить, поскольку интегральная энергетика импульса остается меньше предела разрушения. Даже при большом пиковом напряжении на нелинейном элементе, но при малой длительности его действия общая энергия (доза) поглощаемого излучения остается относительно малой. Для наступления необратимых процессов важен именно энергетический предел, и он существует как для электронных приборов [12], так и для биологических тканей [13].

Из результатов, представленных на рис. 4 видно, что восстановленные профили имеет форму, в точности повторяющие заданные, но, возможно, с некоторым систематическим смещением. Причина этого смещения состоит в том, что излучаемое поле не содержит в себе постоянной составляющей. Таким образом, при прямом использовании предложенного алгоритма восстановление возможно только с точностью до некоторой константы. Константу смещения можно восстановить, используя в качестве дополнительного нормировочного соотношения тот факт, что во временном представлении при нулевом значении напряжения () ток, наведенный на нелинейном элементе, тоже должен быть равен нулю (). Это соотношение равнозначно условию пассивности нелинейного элемента: при отсутствии напряжения нет и тока. Таким образом, по значениям рассеянного поля может быть восстановлен достаточно произвольный вид вольтамперной характеристики нелинейного элемента.

Обратная задача восстановления вольтамперной характеристики нелинейного элемента по измерениям рассеянного сверхширокополосного поля сводится к простому алгебраическому обращению полученных уравнений. Искомая вольтамперная зависимость находится при этом с точностью до константы, связанной с отсутствием в рассеянном поле составляющих на нулевой частоте. Значение этой константы восстанавливается из условия нормировки, соответствующего требованию пассивности нелинейности.

1. Иммореев И.Я. Сверхширокополосные радары: новые возможности, необычные проблемы, системные особенности // Вестник МГТУ. Сер. Приборостроение, 1998, № 4. - С. 25-56.

2. Нелинейные электромагнитные волны / Под ред. П.Усленги. -М.: Мир, 1983. - 312 с.

3. Штейншлейгер В.Б. Нелинейное рассеяние радиоволн металлическими объектами // Успехи физических наук, том 142, 1984. - С. 131-145.

4. Кузнецов А.С., Кутин Г.И. Методы исследования эффекта нелинейного рассеяния электромагнитных волн // Зарубежная радиоэлектроника, № 4, 1986. - С. 41-53.

5. Семенов В.С., Парватов Г.Н., Попов А.А., Рябцев А.П. Использование эффекта нелинейного рассеяния радиоволн для контроля и диагностики // Дефектоскопия, 1999, № 9, с. 85-94.

6. Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн. - М.: Наука. Гл. ред. физ.-мат. лит., 1979. - 384 с.

7. Мейнке Х., Гундлах Ф. Радиотехнический справочник. - М.-Л.: Гос. энергетич. изд-во, 1960. - 416 с.

8. Марков Г.Т.,Чаплин А.Ф. Возбуждение электромагнитных волн. - М.-Л.: Энергия, 1967. - 376 с.

9. Тихонов А.Н., Арсенин В.Я., Тимонов А.А. Математические задачи компьютерной томографии. - М.: Наука, 1987. - 160 с.

10. Якубов В.П., Машаруев М.Л., Славгородский С.А., Лосев Д.В., Шипилов С.Э. Микроволновая томография неоднородных сред // Оптика атмосферы и океана, 1997, т. 10, № 12, с.1500-1507.

11. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. - М.: Наука, 1986. - 287 с.

12. Белобородов П.Ю., Толбанов О.П., Хлудков С.С. Влияние процессов перезарядки глубоких центров на задержку пробоя арсенид-галлиевых структур, компенсированных железом // Физика и техника полупроводников, 1988, Т. 22, вып. 4, с. 755-757.

13. Gandhi Om P. State of Knowledge for Electromagnetic Absorbed Dose in Man and Animals // Proceedings IEEE, 1980, V. 68, N. 1, pp. 24-32.

Авторы:
Якубов Владимир Петрович, е-mail: yvlp@ic.tsu.ru;
Лосев Дмитрий Витальевич,
Мальцев Артем Игоревич.