|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 3, 2003 |
|
исследование эффекта перемежаемости В СИСТЕМЕ СВЯЗАННЫХ НЕЛИНЕЙНЫХ ОСЦИЛЛЯТОРОВ
В. В. Копытов, e-mail: kopytov@stavsu.ru , К. С. Костенко.
филиал Ростовского военного института РВ (г. Ставрополь)
Получена 5 марта 2003 г.
Проведено экспериментальное исследование эффекта перемежаемости, возникающего в системе связанных нелинейных осцилляторов с внешним гармоническим воздействием. Рассмотрены зависимости числовых характеристик длительности импульса и ламинарной фазы стохастического сигнала при переходе к хаосу через перемежаемость от параметров нелинейной системы и уровня входного воздействия и проведена оценка их законов распределения.
1. введение
Известно [1-3], что под перемежаемостью в нелинейных динамических системах понимают такой вид стохастических колебаний, при которых сигнал, развивающийся во времени почти периодически (ламинарные фазы движения), случайным образом сменяется относительно короткими турбулентными вспышками. Замечено также, что число хаотических всплесков может изменяться за счет внешнего воздействия на систему, а это означает, что перемежаемость представляет непрерывный переход от регулярного движения к хаотическому. При этом, как показано во многих работах [1-3], основным механизмом возникновения данного явления является перемежаемость 1-го рода как следствие эффекта обратной касательной бифуркации. В данном случае, для простейших нелинейных систем, описываемых одномерным квадратичным отображением, например для нелинейного RCL-осциллятора находящегося под внешним воздействием в виде d-импульсов, установлено, что средняя длительность ламинарной фазы обратно пропорциональна корню квадратному от величины отклонения внешнего управляющего параметра от значения, при котором возникает перемежаемость. Однако данная теория объясняет лишь появление длинных ламинарных областей и ничего не говорит об описании хаотических всплесков, что требует проведения дополнительных исследований. Кроме этого, большой интерес вызывает исследование эффекта перемежаемости в более сложных нелинейных системах, а именно в связанных неавтономных нелинейных динамических системах (ННДС), и получение вероятностного описания сигнала в зависимости от параметров нелинейной системы и внешнего воздействия.
Целью работы является исследование характеристик стохастического сигнала при переходе к хаосу через перемежаемость в связанных ННДС в зависимости от параметров системы и внешнего воздействия.
По причине малой изученности явления исследование характеристик стохастических колебаний получаемых в результате перемежаемости целесообразно проводить методом аналогового моделирования. Это позволяет с достаточной точностью задавать параметры нелинейной системы и осуществлять измерение параметров стохастических колебаний радиоизмерительными приборами. Синтез модели, при этом, осуществляется методами аналоговой вычислительной техники, которые применительно к линейным цепям, обеспечивают создание неавтономных динамических систем со стабильными характеристиками.
2. разработка аналоговой модели неавтономной нелинейной динамической системы
Синтез аналоговой модели ННДС для экспериментального исследования стохастических колебаний осуществлялся исходя из требования, чтобы нелинейность динамической системы соответствовала наиболее широко распространенной модели, а именно осциллятору Дуффинга [3]. Эта модель достаточно хорошо описывает многие радиофизические системы, такие как сегнетоэлектрические резонаторы и контуры с ферромагнетиками, взаимодействие связанных зарядов с полем электромагнитной волны и другие. При гармоническом воздействии это уравнение сводится к одномерному квадратичному отображению.
Дифференциальное уравнение обобщенного осциллятора Дуффинга под внешним гармоническим воздействием имеет вид
где ![]() - малосигнальная резонансная частота ННДС, соответствующая
амплитуде колебаний сигнала Х®0;
- малосигнальная резонансная частота ННДС, соответствующая
амплитуде колебаний сигнала Х®0;
d - затухание ННДС, однозначно связанное с ее добротностью![]() ;
;
a - коэффициент, определяющий уровень нелинейности;
Uвх – амплитуда внешнего гармонического воздействия;
w - частота внешнего гармонического воздействия.
При магнитной связи между осцилляторами Дуффинга система дифференциальных уравнений имеет следующий вид
где смысл всех параметров совпадает с отмечавшимися выше, а коэффициент k учитывает связь между осцилляторами.
Как видно из выражения (2), данная ННДС состоит из двух одинаковых одиночных нелинейных осцилляторов и связи между ними. С целью обеспечения большей гибкости настройки и применения ННДС синтез функциональной схемы модели целесообразно производить таким образом, чтобы цепи, соответствующие линейным и нелинейным членам уравнения, были разделены, для чего представим одно из уравнений системы (2) в виде
Согласно (3) нелинейность
осциллятора G1(t) может быть обеспечена формированием члена ![]() аддитивного с внешним
воздействием
аддитивного с внешним
воздействием ![]() и
сигналом связи между осцилляторами
и
сигналом связи между осцилляторами ![]() . Сигналы, пропорциональные
. Сигналы, пропорциональные ![]() и
и ![]() , можно получить двойным интегрированием
, можно получить двойным интегрированием
![]() .
Соответственно из (3) следует, что линейная часть каждого из связанных
осцилляторов, рассматриваемой ННДС, должна содержать суммирующий инвертор, два
интегратора и инвертор внутренней цепи обратной связи. На суммирующий инвертор,
кроме сигналов линейной части осцилляторов, подается также сигнал нелинейности G1(t).
Напряжение, пропорциональное нелинейной поправке формируется с помощью каскада
на аналоговых перемножителях.
.
Соответственно из (3) следует, что линейная часть каждого из связанных
осцилляторов, рассматриваемой ННДС, должна содержать суммирующий инвертор, два
интегратора и инвертор внутренней цепи обратной связи. На суммирующий инвертор,
кроме сигналов линейной части осцилляторов, подается также сигнал нелинейности G1(t).
Напряжение, пропорциональное нелинейной поправке формируется с помощью каскада
на аналоговых перемножителях.
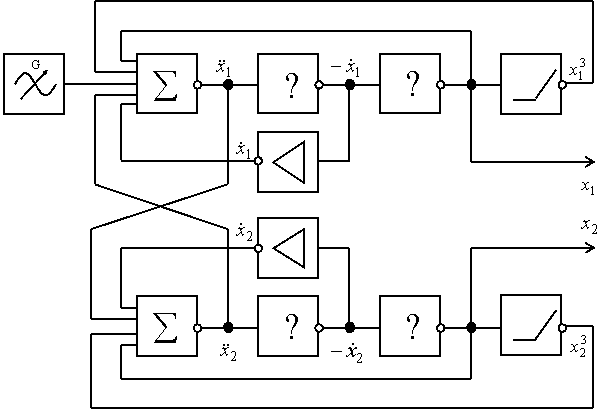
Структурная схема аналоговой модели связанных осцилляторов Дуффинга показана на рисунке 1.
Рисунок 1 - Структурная схема аналоговой модели связанных осцилляторов Дуффинга
Малосигнальная резонансная частота каждого нелинейного осциллятора выбирается исходя из условия возможности измерения параметров хаотических колебаний типовыми радиоизмерительными приборами и ограничения на величину динамической погрешности, определяемой используемыми операционными усилителями. Для удовлетворения этих требований малосигнальная резонансная частота каждого нелинейного осциллятора f0 была выбрана равной 3 кГц. Динамические погрешности при использовании высокочастотных операционных усилителей при этом сводятся к минимуму.
Для определения условий возникновения стохастических колебаний в модели предусмотрено изменение в широких пределах и небольшим шагом добротности каждого осциллятора Q1,2 (от 5 до 200), коэффициента связи между осцилляторами k (от 0,01 до 0,1), коэффициента нелинейности каждого осциллятора a1,2 (от 0,1 до 1).
Синтезированная таким образом модель нелинейной динамической системы позволяет исследовать процессы в колебательных системах второго порядка при различных видах входного воздействия, параметра нелинейности и диссипативности исследуемой системы. Собранная с использованием современных быстродействующих операционных усилителей, модель обладает малой динамической погрешностью (менее 0,25%). Статическая погрешность, дискретно устанавливаемых параметров, не превышает 1%.
3. результаты ЭКСПЕРИМЕНТАЛЬНых исследований
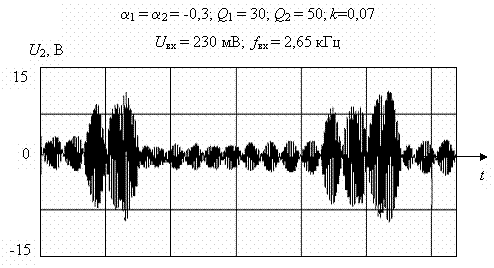
Экспериментальные исследования, проведенные на разработанной аналоговой модели, показали, что основным механизмом перехода к хаосу в связанных нелинейных осцилляторах при коэффициенте связи близком к предельному является последовательность бифуркаций на двумерном торе. Начиная с некоторого значения амплитуды внешнего гармонического сигнала, в системе возникает амплитудная автомодуляция при которой к спектру входного сигнала добавляются боковые составляющие, отвечающие режиму резонансных биений. Дальнейшее последовательное уменьшение частоты входного сигнала приводит к тому, что в системе происходит последовательность бифуркаций удвоения периода частоты биений, сопровождающаяся возникновением субгармонических составляющих в энергетическом спектре колебаний ННДС. С некоторого значения частоты входного воздействия в эксперименте регистрируется сплошной спектр с шириной определяемой амплитудно-частотной характеристикой исследуемой системы связанных нелинейных осцилляторов. Дальнейшее уменьшение частоты входного воздействия приводит к срыву хаотического режима. Именно на границе срыва наблюдаются характерные эффекты перемежаемости с резким увеличением амплитуды сигнала в системе. Осциллограмма стохастического сигнала в системе связанных осцилляторов Дуффинга при возникновении эффекта перемежаемости показана на рисунке 2.
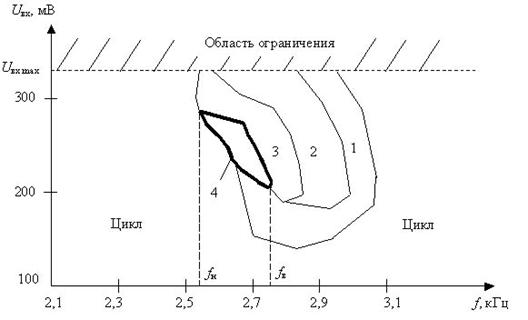
На рисунке 3 показано численное построение бифуркационной диаграммы на выбранной плоскости управляющих параметров амплитуда-частота входного воздействия для одного из вариантов значений параметров исследуемой системы, при которых возникает эффект перемежаемости. На данном рисунке цифрами указаны следующие характерные режимы работы системы связанных осцилляторов Дуффинга:
1 – область возникновения биений между связанными нелинейными осцилляторами;
2 – область последовательного удвоения периода частоты биений между осцилляторами;
3 – область стохастичности;
4 – область возникновения эффектов перемежаемости.
Рисунок 2 - Осциллограмма стохастического сигнала в системе связанных осцилляторов Дуффинга при возникновении эффекта перемежаемости (физический эксперимент)
Рисунок 3 - Бифуркационная диаграмма системы связанных нелинейных осцилляторов при a1= a2 = -0,3, Q1 = 30, Q2 = 50, k=0,07 (физический эксперимент)
Экспериментальные исследования показали, что для получения эффектов перемежаемости в системе связанных осцилляторов Дуффинга необходимо, чтобы параметры модели лежали в следующих пределах:
Коэффициент связи между осцилляторами в любом случае должен быть близким к предельному значению. Увеличение добротности первого осциллятора приводит к смещению и сужению области перемежаемости и, следовательно, к уменьшению области допустимых значений входного воздействия, при которых существуют эффекты перемежаемости. При добротности первого осциллятора выше 50 наблюдать явление перемежаемости затруднительно из-за срыва стохастического режима в системе, так как ширина области перемежаемости становится сравнимой с величиной нестабильности вынуждающего воздействия. Изменение коэффициентов функции нелинейности a1,2 осцилляторов в указанных пределах незначительно влияет на ширину области стохастичности.
Для получения вероятностного описания стохастического сигнала при переходе к хаосу через перемежаемость в зависимости от параметров исследуемой системы возникает задача статистической обработки данных: конкретных значений длительности хаотического импульса tи1, tи2, …, tип и длительности ламинарной фазы tл1, tл2, …, tлп, где п – объем выборки полученной в результате независимых измерений.
Для получения достоверных значений числовых характеристик и закона распределения исследуемых случайных величин был проведен требуемый объем выборки экспериментальных данных с числом отсчетов п не меньшим, чем [4]
где РД – значение доверительной вероятности;
потб – число отбрасываемых отсчетов с каждого из концов выборки.
Для определения числовых характеристик случайной величины Х не требуется какого-либо группирования экспериментальных данных. Эти оценки находятся непосредственно по исходной неупорядоченной выборке. Выборочные среднее и «несмещенное» среднее квадратическое отклонение (СКО) определяются соответственно следующими выражениями [4]
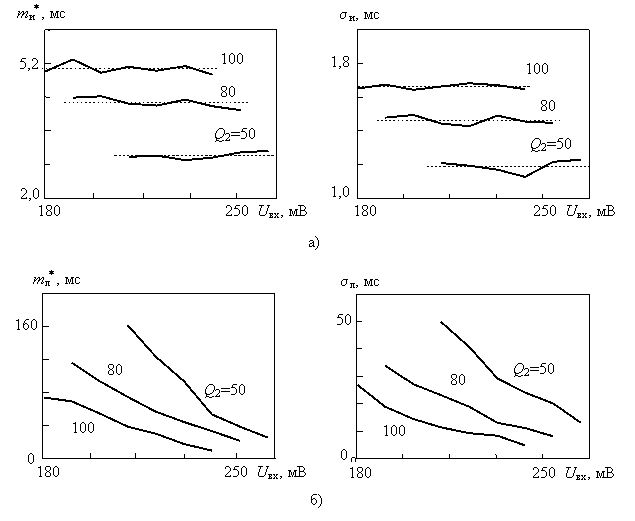
Проведенные расчеты показали, что числовые характеристики длительности хаотического импульса ти* и sи при изменении амплитуды внешнего воздействия практически остаются постоянными и при большом числе независимых измерений стремятся к некоторым постоянным значениям, которые определяются только параметрами системы связанных осцилляторов Дуффинга. Числовые характеристики ламинарной фазы тл* и sл напротив зависят как от параметров системы, так и от уровня внешнего воздействия, уменьшаясь с ростом амплитуды входного сигнала, что подтверждает известные теоретические исследования. Пример построения графиков по результатам экспериментальных исследований значений числовых характеристик стохастического сигнала при переходе к хаосу через перемежаемость в зависимости от параметров системы связанных осцилляторов Дуффинга и амплитуды внешнего гармонического воздействия приведены на рисунке 4.
Рисунок 4 – Зависимость числовых характеристик длительности хаотического импульса (а) и ламинарной фазы (б) в зависимости от амплитуды внешнего воздействия и добротности второго осциллятора Q2 при a1= a2=-0,3, Q1=30
Случайная величина может быть описана достаточно полно аналитической кривой плотности распределения. Для определения формы распределения длительности хаотического импульса и ламинарной фазы стохастического сигнала при переходе к хаосу через перемежаемость выборка полученных экспериментальных данных должна быть представлена в виде гистограммы, состоящей из столбцов с определенной протяженностью соответствующих им интервалов. При этом общепринято делать эти интервалы одинаковыми. Для более наглядного отражения формы распределения строится полигон распределения, путем соединения прямыми середин верхних оснований каждого столбца гистограммы. Идентификация формы распределения сводится к выбору аналитической модели, которая не противоречит данной конкретной выборке экспериментальных данных, т.е. необходимо провести аппроксимацию гистограммы подходящим аналитическим выражением какой-либо теоретической плотности вероятности (выравнивание статистических данных). При этом аппроксимация должна быть в определенном смысле наилучшей.
Для оценки, насколько хорошо
выбранный теоретический закон распределения согласуется с результатами
наблюдений, использовался критерий согласия ![]() [4]. По этому критерию за меру расхождения результатов
наблюдения и теоретического распределения принимают величину
[4]. По этому критерию за меру расхождения результатов
наблюдения и теоретического распределения принимают величину
где ![]() - относительная частота;
- относительная частота;
![]() - вероятность попадания случайной величины Х в i-й интервал.
- вероятность попадания случайной величины Х в i-й интервал.
Случайная величина ![]() , независимо от
распределения величины Х, при
, независимо от
распределения величины Х, при ![]() асимптотически распределена по закону
асимптотически распределена по закону ![]() с
с ![]() степенями свободы, где s – число параметров теоретического
распределения, оцениваемых по результатам наблюдений.
степенями свободы, где s – число параметров теоретического
распределения, оцениваемых по результатам наблюдений.
Проведенные исследования при различных значениях параметров системы показали, что длительность всплеска и длительность ламинарной фазы распределены по нормальному закону
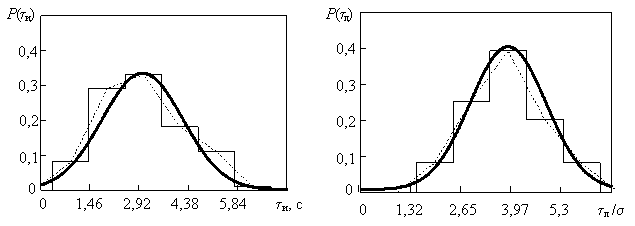
с математическим ожиданием и СКО определяемым по формулам (6) и (7) для выборочных значений исследуемой величины, что наглядно иллюстрируется результатами приведенными на рисунке 5, на котором в качестве примера показано построение гистограмм экспериментальных значений длительности хаотического импульса и ламинарной фазы и соответствующие им законы распределения при a1= a2=-0,3, Q1=30, Q2=50, k=0,07 и амплитуде внешнего воздействия Uвх=220 мВ. Точками на рисунке показаны полигоны распределения исследуемых случайных величин, сплошной линией выбранные теоретические законы распределения.
Рисунок 5 – Пример проведения аппроксимации гистограмм экспериментальных значений длительности хаотического импульса tи и ламинарной фазы tл при a1= a2=-0,3, Q1=30, Q2=50, k=0,07, Uвх=220 мВ
4. ВЫВОДЫ
Проведенные экспериментальные исследования стохастического сигнала при переходе к хаосу через перемежаемость на аналоговой модели связанных нелинейных осцилляторов показали, что длительность всплеска и длительность ламинарной фазы распределены по нормальному закону. При этом числовые характеристики длительности хаотического всплеска, в отличие от длительности ламинарной фазы, не зависят от уровня внешнего воздействия на систему и определяются только параметрами нелинейной системы. Полученные выводы могут быть использованы при проведении вероятностного описания эффекта перемежаемости в связанных нелинейных системах второго порядка.
1. Анищенко В.С. Сложные колебания в простых системах: Механизмы возникновения, структура и свойства динамического хаоса в радиофизических системах. - М.: Наука. Гл. ред. физ.-мат. лит., 1990.
2. Шустер Г. Детерминированный хаос: Введение: Пер. с англ. - М.: Мир, 1998.
3. Неймарк Ю.И., Ланда П.С. Стохастические и хаотические колебания. - М.: Наука. Гл. ред. физ.-мат. лит., 1997.
4. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. – Л.: Энергоатомиздат. Ленингр. отд-ние, 1991.
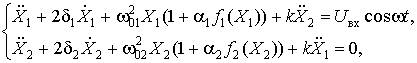 (2)
(2)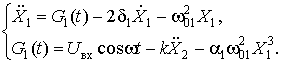 (3)
(3)
 (4)
(4)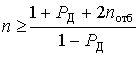 ,
, 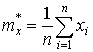 , (6)
, (6) .
(7)
.
(7)
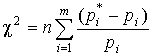 ,
(8)
,
(8) (9)
(9)