УДК 621.396.96:621.391.26Метод повышения эффективности РЛС для обнаружения людей за оптически непрозрачными преградами
О. В. Сытник И. А. Вязьмитинов, Е. И. Мирошниченко, Ю. А. КопыловИнститут радиофизики и электроники им. А. Я. Усикова НАН Украины
Получена 12 марта 2008 г.
Рассмотрены возможности снижения уровня боковых лепестков автокорреляционной функции ФКМ зондирующих сигналов и проблемы их практической реализации в аппаратуре. Предложена оптимальная фазо-амплитудная внутриимпульсная модуляция, позволяющая снизить боковые лепестки и одновременно повысить частоту следования зондирующих посылок. Исследованы факторы, влияющие на характеристики таких сигналов и предложен критерий их реализуемости в аппаратуре.
Введение.
Алгоритмы обработки сигналов в радиолокаторе с квазинепрерывным зондирующим сигналом, предназначенным для обнаружения объектов, скрытых за оптически непрозрачными препятствиями, как правило, строятся по принципу оптимальной корреляционной обработки или согласованной фильтрации [1 – 5].
Зондирующие сигналы для таких РЛС выбирают исходя из требования обеспечения необходимой разрешающей способности и помехоустойчивости. При этом функцию неопределенности сигнала стараются сделать карандашного вида в соответствующей плоскости с минимальным уровнем боковых лепестков. Для этого применяют различные сложные виды модуляции [3, 5, 6]. Наиболее распространенными из них являются: частотно-модулированные сигналы; многочастотные сигналы; фазо-манипулированные сигналы; сигналы с кодовой фазовой модуляцией; дискретные частотные сигналы или сигналы с кодовой частотной модуляцией; составные сигналы с кодовой частотной модуляцией и ряд сигналов, являющихся комбинацией нескольких видов модуляции. Чем уже главный пик функции неопределенности сигнала и чем ниже уровень ее боковых лепестков, тем, соответственно, выше разрешение и помехоустойчивость РЛС. Под термином «помехоустойчивость» в данной работе имеется ввиду устойчивость РЛС к помехам, обусловленным отражениями зондирующего сигнала от объектов, не являющихся целями и расположенных вне анализируемого строба (частотного, временного). Такие сигналы в литературе называют сигналами с большой базой или сверхширокополосными сигналами (СШП).
Одной из разновидностей СШП сигналов являются фазо-манипулированные сигналы, представляющие кодированную последовательность радиоимпульсов, начальные фазы которых изменяются по заданному закону. Кодовые последовательности максимальной длины или М-последовательности обладают весьма важными для радиолокации свойствами [6]:
· М-последовательности являются периодическими с периодом
, где
−число элементарных импульсов в последовательности;
−длительность элементарного импульса;
· Уровень боковых лепестков функции неопределенности для периодической последовательности составляет −
, а для одиночной последовательности импульсов −
;
· Импульсы в одном периоде последовательности, различающиеся фазами, частотами, длительностями, распределены равновероятно, что дает основание считать эти сигналы псевдослучайными;
· Формирование М-последовательностей осуществляется достаточно просто на сдвиговых регистрах, причем число разрядов регистра
определяется длиной одного периода последовательности -
из соотношения
.
Целью настоящей работы является исследование возможностей снижения уровня боковых лепестков функции неопределенности сигналов, модулированных М-последовательностями.
Постановка задачи.
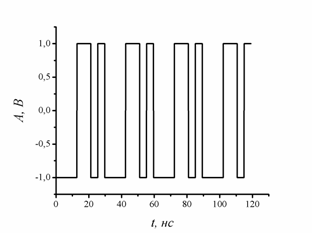
На рис.1 показан фрагмент модулирующей функции, образованной периодической последовательностью (здесь два периода М-последовательности с
).
Рис.1. Фрагмент М-последовательности
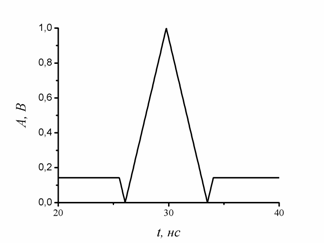
Рис.2. Сечение по оси времени функции неопределенности ФКМ-сигнала
Сечение по оси времени функции неопределенности радиосигнала, модулированного такой М-последовательностью показано на рис.2. Уровень боковых лепестков, как и предсказывает теория, составляет 1/7 или минус 8,5 дБ.
Рассмотрим возможность минимизации боковых лепестков функции неопределенности ФКМ-сигнала. Обозначим символом
М-последовательность, длительность одного периода которой равна
. В дискретном времени при условии, что
, алгоритм вычисления элементов последовательности можно записать в следующем виде:
Излучаемый локатором радиосигнал есть произведение несущего гармонического сигнала
где
− вектор параметров, на модулирующую функцию (1) -
Мощность сигнала распределяется между боковыми лепестками функции неопределенности -
и главным лепестком -
где символом *− обозначена операция комплексного сопряжения, а пределы интегрирования во временной и частотной областях определяются соответствующим видом модуляции сигнала.
Отношение
можно рассматривать как целевую функцию параметрической оптимизационной задачи.
Алгоритм решения задачи.
Решением оптимизационной задачи (6) есть оценка
параметра
-
где
− область определения вектора
.
Традиционный способ вычисления оценки (7) состоит в решении системы уравнений -
Аналитическое решение (8) оказывается достаточно трудоемко, поэтому воспользуемся процедурой численной минимизации, основанной на методе Ньютона [7]
где
− величина, определяющая длину шага процедуры поиска экстремума целевой функции
.
Один из способов вычисления длины шага состоит в вычислении
:
В простейшем случае, когда вектор
составлен из одного параметра, например
или
, зондирующий сигнал формируется относительно просто. В частности, при оптимизации целевой функции по параметру
сигнал формируется в соответствии с соотношением
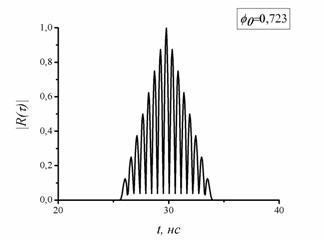
На рис. 3 показан фрагмент модуля автокорреляционной функции сигнала (11) при
, что соответствует ФКМ радиосигналу без внутриимпульсной фазовой модуляции.
Рис. 3. Модуль автокорреляционной функции сигнала (11) при
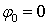
Рис.4. Модуль автокорреляционной функции при
Уровень бокового лепестка этой функции соответствует теоретическому пределу равному
, где
. На рис. 4 показан фрагмент модуля автокорреляционной функции сигнала (11) при параметре
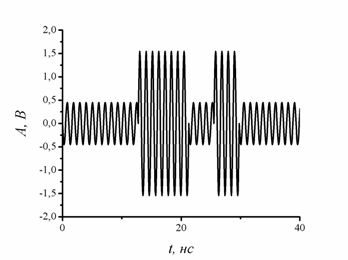
, полученном при оптимизации функции (9). Уровень бокового лепестка при этом составляет минус 150 дБ. Этот же результат получается при амплитудной модуляции М-последовательности. На рис. 5 показан вид такого сигнала при оптимальном значении
.
Рис. 5. Фрагмент ФКМ-сигнала, модулированного по амплитуде
Зондирующий сигнал при этом формируется в соответствии с алгоритмом
Одновременная амплитудно-фазовая модуляция приводит к снижению бокового лепестка еще на порядок. Достичь нулевого уровня бокового лепестка не удается из-за неизбежных вычислительных ошибок рекуррентной процедуры минимизации целевой функции (6), которые не позволяют отыскать истинное значение параметра
, а лишь его некоторую окрестность -
. На рис. 6 показана зависимость значений оптимальных коэффициентов фазовой модуляции от параметра
, определяющего длину последовательности.
Рис. 6. Зависимость оптимального фазового сдвига от длины М-последовательности
Из рис. 6 видно, что при увеличении длины последовательности значение оптимального фазового сдвига асимптотически стремится к нулю и при
можно считать, что оптимальный сигнал с внутриимпульсной фазовой модуляцией практически не отличается от обычного ФКМ-сигнала. Исследования показывают, что с ростом длины периода модулирующей ПСП относительная чувствительность к искажениям сигнала будет падать.
Аналитическим критерием для выбора граничной длины последовательности может служить следующее соотношение
где
некоторое число, определяющее возможность технической реализации сигнала с внутриимпульсной модуляцией в аппаратуре.
Оценка целесообразности усложнения сигнала.
Неизбежное усложнение сигнала при снижении боковых лепестков автокорреляционной функции существенно ужесточает требования к устройствам формирования и трактам передачи - приема сигналов. Так, при ошибке установки фазового множителя в одну тысячную радиана уровень бокового лепестка возрастает с минус 150 дБ до минус 36 дБ. При амплитудной модуляции ошибка относительно оптимального значения коэффициента А в одну тысячную приводит к возрастанию бокового лепестка с минус 150 дБ до минус 43 дБ. Если же ошибки в установке параметров составляют 0,1 от оптимальных, что может быть реализовано в аппаратуре, то боковой лепесток функции неопределенности возрастет до минус 15 дБ, что на 7 - 7,5 дБ лучше, чем при отсутствии дополнительной фазовой и амплитудной модуляции.
С другой стороны снизить боковой лепесток функции неопределенности можно без усложнения сигнала путем увеличения
. Так при
уровень бокового лепестка составит примерно минус 15 дБ. Следует отметить, что и обычные (т.е. без дополнительной АМ-ФМ модуляции) ФКМ-сигналы чувствительны к ошибкам, возникающим при их формировании [8]. Поэтому длину М-последовательности в реальных радиолокационных устройствах неограниченно увеличивать также нецелесообразно.
Рассмотрим влияние ошибок, возникающих в аппаратуре при формировании, передаче, приеме и обработке ФКМ-радиосигналов на их свойства.
Оценка влияния ошибок формирования ФКМ-сигнала на его свойства.
Всю совокупность факторов, влияющих на характеристики сигнала, можно разделить на две группы: флуктуационные и детерминированные.
К флуктуационным факторам относятся: фазо-частотные нестабильности опорных генераторов; шумы различного рода; сигналы, просачивающиеся из передатчика непосредственно на вход приемника и после корреляционной обработки с опорным сигналом образующие шумоподобные процессы, и другие факторы.
К детерминированным факторам относятся: недостаточная широкополосность формирующих цепей; асимметричность модулирующей функции; некогерентность модулирующей функции и несущего колебания; отличие формы опорного и зондирующего сигналов и т.п.
В более общем виде аналитическое выражение для сигнала, модулированного псевдослучайной М- последовательностью, представим в виде [9]
где
;
— постоянная амплитуда;
или p — фаза сигнала; N=2k-1; k-целое число;
—длительность элементарного импульса, образующего последовательность.
Его двумерная корреляционная функция записывается как:
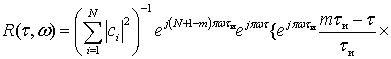
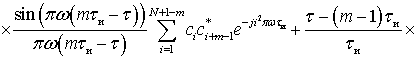
при
,
, а его нормированный спектр —
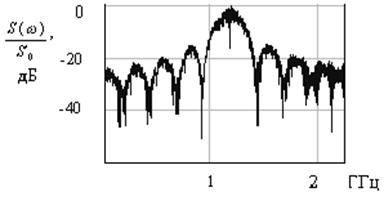
показан на рис.7. Здесь для наглядности показан фрагмент частотной оси, где сосредоточены основные компоненты спектра сигнала. Характерной особенностью такого сигналa, как видно из рис.7, является пониженный уровень немодулированного несущего колебания, который в идеальном случае стремится к нулю.
Рис.7. Нормированный спектр сигнала
Широкая полоса спектра и отсутствие периодического немодулированного колебания позволяет реализовать алгоритмы обнаружения и идентификации объектов в локационных системах, подобных [5], при ослаблении полезного сигнала в препятствиях на 40-50 дБ и уровнях коррелированных помех, превышающих сигнал на 50-70 дБ.
Из-за инерционности формирующих цепей появляются выраженные переходные процессы, паразитная амплитудная модуляция и ряд других эффектов, которые искажают как форму так и спектр излучаемых и опорных колебаний.
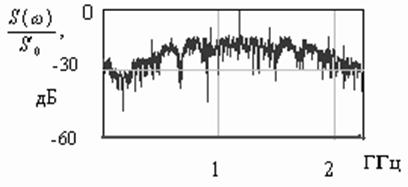
Очевидно, что искажения, вносимые во временную реализацию сигнала, отражаются на его корреляционных свойствах. Появляется дополнительная паразитная амплитудная модуляция, нарушаются фазовые соотношения между отдельными компонентами ПСП, возникает асимметрия относительно нулевой оси несущей и ряд других нежелательных явлений, которые снижают характеристики локационной системы в целом. На рис. 8 представлена спектральная плотность искаженного сигнала.
Рис. 8. Спектральная плотность искаженного сигнала
Рис. 8 дает представление об искажениях, вносимых в сигнал, а именно о появлении значительного уровня немодулированного несущего колебания и паразитной амплитудной модуляции.
В случае, когда искажения сигнала заданы детерминированными функциями в координатах доплеровское смещение − задержка, их влияние на параметры автокорреляционной функции сигнала удобнее учесть, например, в виде следующих функций ошибок.
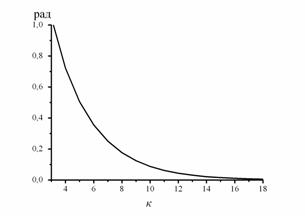
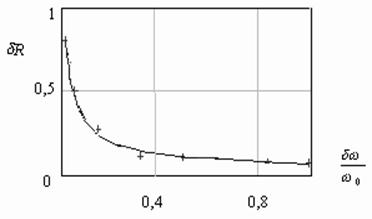
Так, для фазо-манипулированного псевдослучайного сигнала с N=15, зависимость уровня остаточного бокового лепестка автокорреляционной функции от ширины полосы пропускания формирующих цепей и радиотракта представлена на рис. 9.
Рис.9. Зависимость уровня бокового лепестка АКФ от ширины полосы
пропускания формирующего тракта для k=4
Здесь по оси ординат отложена величина, определяющая предельно достижимый уровень бокового лепестка автокорреляционной функции -
- сигнала, модулированного псевдослучайной М- последовательностью, а по оси абсцисс - выраженное в процентах отношение ширины полосы пропускания формирующей цепи к максимальному значению частоты эффективного спектра сигнала. Точками на графике показаны значения уровня бокового лепестка АКФ, полученные при численном моделировании аппаратурных эффектов. Как видно из рис.9, при отсутствии частотных искажений в радиотрактах уровень бокового лепестка АКФ сигнала, модулированного по фазе периодической ПСП с периодом N, составляет – 1/N. Это соответствует известному теоретическому пределу [6]. При ограничении спектра модулированного сигнала уровень бокового лепестка возрастает и при 50%-ном ограничении достигает уровня
, что соответствует непериодической автокорреляционной функции. Дальнейшее ограничение спектра радиосигнала приводит практически к полному развалу АКФ и, как результат, к невозможности использовать сигнал для практических целей.
Искажения спектра излучаемого локатором сигнала и опорных колебаний, поступающих на коррелятор, за счет асимметрии между положительными и отрицательными уровнями и длительностями модулирующих колебаний приводят к значительному росту помех в области боковых лепестков АКФ и ухудшению пространственного разрешения и характеристик обнаружения локатора. Зависимость уровня бокового лепестка от коэффициента асимметрии показана на рис.10
Коэффициент асимметрии определялся как
где
− длительность неискаженного элементарного импульса, образующего М- последовательность; индексы "+" и "−" означают длительность положительного и отрицательного элементарного импульса при асимметричных искажениях.
Рис.10. Зависимость уровня бокового лепестка АКФ от величины асимметричных искажений сигнала для k=4.
Как видно из графика, приведенного на рис.10 при отсутствии асимметричных искажений сигнала
уровень бокового лепестка АКФ сигнала, модулированного ПСП с периодом N=15, также составляет величину равную 1/15. При появлении асимметрии сигнала уровень боковых лепестков возрастает и при 50%-ной асимметрии преимущества периодической ПСП по отношению к усеченной полностью утрачиваются. Следует отметить, что указанные искажения приводят к появлению паразитной амплитудной модуляции излучаемого сигнала, а также к появлению значительной доли немодулированного несущего колебания в спектре зондирующего сигнала. Это приводит к тому, что при отражении от посторонних объектов сигнал немодулированного несущего колебания, возвращаясь на вход приемника, образует мультипликативную помеху работе локатора, снижая способность локатора к разрешению целей, обусловленную модуляцией сигнала ПСП. Поэтому остаточный уровень подавленного сигнала несущего колебания должен быть в пределах уровня «псевдошума», образованного боковыми лепестками корреляционной функции сигнала. Если этого достичь по каким-либо причинам не удается, то применение ПСП с низким уровнем бокового лепестка нецелесообразно.
Заключение.
Выбор сигнала и степень сложности его модулирующей функции определяется в первую очередь характером задач, для которых предназначен радиолокатор. Применение достаточно сложного ФКМ-сигнала с внутриимпульсной модуляцией требует создания прецизионной аппаратуры, что неизбежно приведет к существенному возрастанию цены конструкции, но в то же время позволит создать универсальные блоки, которые можно будет использовать как в РЛС для спасателей, так и в РЛС для обнаружения быстролетящих целей. Такая возможность появляется потому, что характеристики сложного сигнала при короткой длине последовательности, т.е. высокой частоте повторения посылок, позволяют иметь необходимые разрешение и помехоустойчивость при возможности измерения допплеровских частот в более широком диапазоне. Кроме того, построение радиолокационных систем с непрерывным излучением и псевдослучайной фазовой модуляцией несущего колебания требует детального анализа и учета всех факторов, которые обуславливают искажения сигналов как в передающем, так и в приемном трактах локатора. Учет искажающих факторов сводится к решению инженерных задач по обеспечению достаточной широкополосности, стабильности электрических параметров и устойчивости характеристик формирующих трактов. При этом зондирующие сигналы РЛС должны быть когерентны модулирующим и вспомогательным сигналам. В противном случае необходимы такие технические решения, которые бы минимизировали разностные искажения между излученным и опорным колебаниями. Один из возможных путей, позволяющих реализовать такие технические решения – это введение симметричных ограничений сигналов по амплитуде в выходных каскадах передатчика и на входе коррелятора приемника. При этом, хотя и теряется часть энергии сигнала, удается сформировать АКФ модулированного сигнала с приемлемыми параметрами. Такие технические решения допустимы в портативных радиолокаторах, где стоимость и габариты системы играют решающую роль.
Наиболее перспективным в настоящее время, с точки зрения авторов, следует считать построение устройств формирования и обработки радиосигналов сложной структуры для радиолокационной аппаратуры, на основе высокоскоростных сигнальных процессоров, работающих с тактовыми частотами в несколько гигагерц. Структурная схема радиолокатора при таком подходе становится предельно простой. Это линейный усилитель мощности, малошумящий линейный усилитель приемника и процессор с периферийными устройствами. Такая схема позволяет не только практически полностью реализовать свойства сигналов, заложенные в их тонкую структуру, но и создавать технологично простые в настройке радиолокационные системы, обработка информации в которых строится на основе оптимальных алгоритмов.
Литература
1. Frank U.A., Kratzer D.L., Sullivan J.L. The Twopound Radar // RCA Eng.-1967. №.2; P.52-54.
2. Доплеровская РЛС для разведки на местности. Сер. Техн. средства развед. служб кап. гос. // ВИНИТИ. – 1997. – № 10. – С. 46-47.
3. Nordwall Bruce D. Ultra-wideband radar detects buried mines // Aviat. Week and Space Technol - 1997. №13.—P. 63-64.
4. Sytnik O.V., Vyazmitinov I.A., Myroshnychenko Y.I. The Features of Radar Developments for People Detection Under Obstructions // Telecommunications and Radio Engineering. ¾ 2004. ¾ Vol.61, ¾ № 10. ¾ P. 875–885.
5. Sytnik O.V., Vyazmitinov I.A., Myroshnychenko, Y.I Kopylov Y.A. Design Problems of Rescue-Radar // Procf of Intern. Conf. Antennas, Radar and Wave Propagation // ARP-2007, Montreal, QC., Canada. – 5/30/2007 – 6/1/2007. – Radar: 566-082.
6. Варакин Л.Е. Системы связи с шумоподобными сигналами. –М.: Радио и связь, 1985.-384 с.
7. Поляк Б.Т. Введение в оптимизацию. – М.: Наука. – 1983. – 384 с.
8.Sytnik O.V., Myroshnychenko, Y.I Kopylov Y.A. Estimation of Implementation Errors Effect on Characteristics of Pseudorandom Radar Signal // Telecommunications and Radio Engineering. ¾ 2003. ¾ Vol.60, № 1&2. ¾ P. 132–140.
9. Справочник по радиолокации / Под ред. М. Сколника. Пер. с англ. Под ред. К.Н.Трофимова. , М.: Сов. радио,1978, Том.3. 528с.
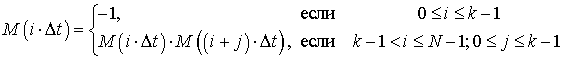 (1)
(1)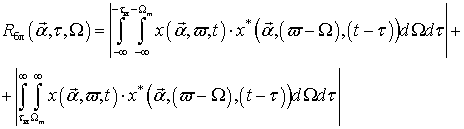 (4)
(4)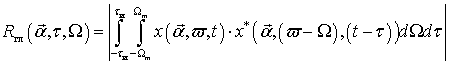 , (5)
, (5)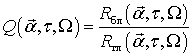 (6)
(6)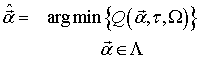 , (7)
, (7)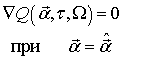 .
. 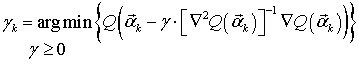 . (10)
. (10)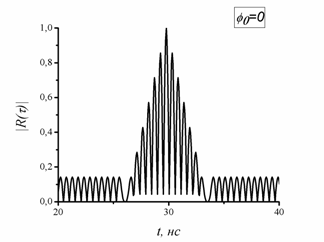
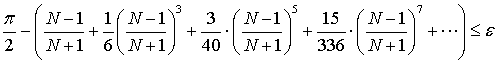 , (13)
, (13)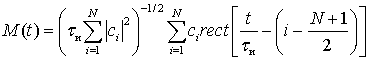 ,
, 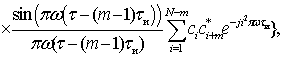
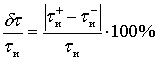 , (16)
, (16)