|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 2, 2009 |
оглавление |
|
|
компьютерное Проектирование и экспериментальнОе исследованиЕ кластерного излучателя на основе EBG структуры
С.Е. Банков, В.А Калошин, Е.В.Фролова
Институт радиотехники и электроники им. В.А.Котельникова РАНПолучена 4 марта 2009 г.
Приведены результаты компьютерного проектирования многоканального кластерного излучателя на основе EBG структуры, образующей решетку неодинаковых связанных волноводов. Численное моделирование матрицы коэффициентов рассеяния выполнено методом конечных элементов. По амплитудно-фазовым распределениям поля в выходной апертуре методом Кирхгофа вычислены диаграммы направленности излучения и исследованы их зависимости от параметров решетки и частоты излучения. Создан макет кластерного излучателя и измерены диаграммы направленности на трех частотах. Проведено сопоставление результатов численного моделирования и физического эксперимента.
Ключевые слова: антенны, численное моделирование в электродинамике, экспериментальная электродинамика.
1. Введение
В системах связи и радиолокации используются многолучевые антенны, содержащие фокусирующую систему (ФС) в виде одного или нескольких зеркал (линз) и линейную или матричную облучающую систему (ОС). При возбуждении каждого входа ОС ФС формирует парциальный луч – остронаправленную диаграмму направленности (ДН), положение которой в пространстве определяется положением входа ОС. Такую схему формирования лучей называет квазиоптической диаграммообразующей схемой (ДОС). Функция, которую выполняет ДОС заключается в оптимальном облучении ФС, при этом диаграмма направленности элемента решетки ОС определяет коэффициент направленного действия (КНД) и уровень боковых лепестков (УБЛ) антенны. Для того, чтобы избежать значительного перелива энергии ОС за апертуру ФС уровень облучения ее края не должен превышать некоторый заданный уровень, который зависит от формы ДН. Это требование ограничивает снизу величину апертуры облучателя и соответственно, расстояние между облучателями. В результате при использовании стандартных (не связанных по входу) облучателей уровень пересечения лучей получается очень низким и в многолучевой диаграмме появляются глубокие провалы. Для того, чтобы избежать появления таких провалов в [1] были описаны различные схемы построение ДОС кластерных ОС, в которых каждый вход эффективно возбуждает несколько выходных элементов ОС. Одна из наиболее эффективных из них представляла собой решетку одинаковых прямоугольных связанных волноводов с фазовращателями. В работе [2] вместо фазовращателей для формирования ДОС предложено использовать решетку неодинаковых по размеру сечения волноводов и представлена феноменологическая модель, основанная на теории связанных волн.
В данной работе исследуется возможность реализации ДОС на основе неодинаковых связанных волноводах в виде двумерной периодической решетки из металлических цилиндров, являющейся моделью electromagnetic bandgap (EBG) структуры [3]. Целью данной работы является синтез и анализ ДОС строгим электродинамическим методом и экспериментальная проверка его результатов.
Следует отметить, что кластерные излучатели представляют интерес не только в качестве ОС, но и для подавления боковых лепестков в разреженных антенных решетках [4]. Постановка задачи там отличается тем, что требуется не минимизация расстояния между элементами в решетке, а максимальная крутизна спадания диаграммы элемента вне сектора сканирования.
2.Электродинамическая модель кластерного излучателя на связанных EBG волноводах и методика её анализа
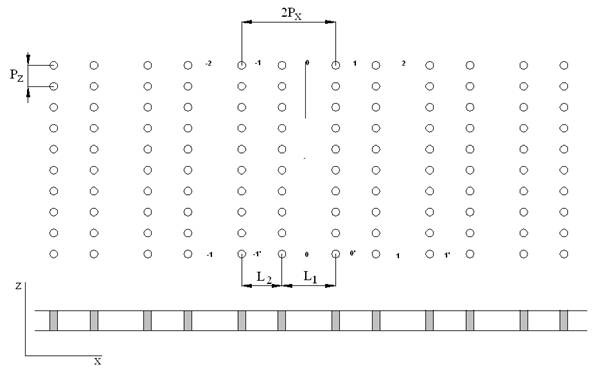
Структура и принцип функционирования ДОС. Исследуемая ДОС показана на рис. 1.
Рис.1. Схема ДОС на связанных волноводах.
Она сформирована металлическими цилиндрами, расположенными между двумя металлическими экранами, образующими плоский волновод. Каждая линейка цилиндров, ориентированная вдоль оси 0z, представляет собой полупрозрачную стенку. Две такие стенки формируют волновод, а решетка цилиндров - систему связанных волноводов.
В структуре, показанной на рис. 1, соседние волноводы имеют различную ширину. Первый имеет ширину
, а второй.
, третий – такую же ширину как первый и т.д. Волноводы, соответственно, имеют разные постоянные распространения
. Активными (возбуждающими) являются волноводные каналы с большей шириной
. Каналы с меньшей шириной
являются пассивными. При возбуждении одного из активных каналов, по мере распространения в нем волны из-за наличия связи между волноводами происходит проникновение поля в соседние каналы в результате чего формируется амплитудно-фазовое распределение на выходе решетки.
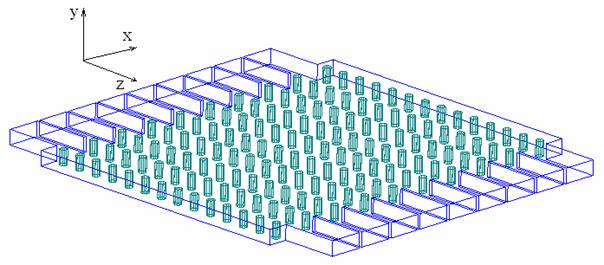
Модель для численного исследования ДОС. Численное моделирование приведенной структуры проводилось методом конечных элементов, Следует отметить, что хотя метод конечных элементов и является строгим электродинамическим методом и успешно применяется для расчета полей в волноводных структурах, однако результат вычислений зависит от правильности выбора модели структуры. При решении внутренней задачи исследуемый объем ограничивается поверхностью структуры. При моделировании вычисляются коэффициенты матрицы рассеяния. Для решения задач, связанных с излучением, исследуемый объем помещается в воздушный бокс, стенки которого отстают от границ структуры на некоторое расстояние, затем вычисляется диаграмма направленности излучения в свободном пространстве. В данной задаче, несмотря на то, что конечной целью моделирования являлось получение именно ДН, на первом этапе проектирования решалась внутренняя задача, т.е. получение матрицы рассеяния. Это было обусловлено нестабильностью результатов моделирования при непосредственных расчетах ДН и их зависимостью от размеров бокса. Итак, в данной задаче была выбрана следующая электродинамическая модель (см. рис.2). Плоский волновод с периодической решеткой цилиндров (EBG структура) помещается в ограниченный объем (бокс), верхняя и нижняя стенки которого совпадают со стенками плоского волновода. Затем этот бокс объединяется с входными и выходными волноводами, образуя единый объем, в пределах которого ищется решение для поля. Полагаем, что внутри исследуемого объема - вакуум, материал, из которого состоят цилиндры – алюминий. На стенках образованного объема, за исключением открытых концов волноводов, требуем выполнения граничных условий для электрического поля на металле. На открытых концах волноводов устанавливаются волноводные порты.
Рис.2. Модель ДОС для электродинамического моделирования.
В данной задаче при моделировании не удается, к сожалению, учесть наличие продольной плоскости симметрии, что позволило бы анализировать только половину структуры и тем самым существенно сократить время вычислений. Для однозначного восстановления фазы в выходных каналах необходимо указать направление калибровочных линий и вектора поляризации поля Е одновременно во всех каналах. Однако при возбуждении центрального волноводного канала невозможно в плоскости порта задать калибровочную линию, так как она лежит в плоскости симметрии.
Целью моделирования на данном этапе является расчет поля в заданном объеме, удовлетворяющего граничным условиям, и вычисление элементов матрицы рассеяния. Модули и фазы коэффициентов матрицы рассеяния в выходных волноводах определяют амплитудно-фазовое распределение в апертуре кластерного излучателя, которое в свою очередь формирует диаграмму направленности.
Модель для расчета ДН ДОС. Выбрав за направление распространения волны в волноводе ось ОZ, за направление поляризации поля Е - ось OY (рис.2), представим апертуру кластера как решетку, состоящую из открытых концов волноводов в Н-плоскости. В рамках приближения Кирхгофа, выражение для ДН кластерной решетки
в плоскости ZX имеет вид:
где
- ДН открытого конца волновода,
- размер широкой стенки волновода,
- его постоянная распространения,
- волновое число свободного пространства,
,
- амплитуды и фазы волн в выходных волноводах ДОС. Они определяются как модули и фазы соответствующих коэффициентов матрицы рассеяния.
Для численного исследования выберем в первом приближении параметры EBG структуры на основе результатов, полученных в рамках теории связанных волн в диапазоне 8 ГГц [2]: Приведем эти параметры: размеры сечений волноводов (23x10) мм; расстояние между осями волноводов 25 мм (зазор между стенками 2 мм), диаметр цилиндров 5 мм, высота - 10 мм, продольный период решетки
=14 мм, поперечный период -
=
= 50 мм, расстояния между стенками в активных и пассивных каналах решетки 25,6 мм и 24,4 мм. Ограничим объем, содержащий EBG структуру, размерами (196x225x10) мм. Количество цилиндров в этом объеме - 140 (14 рядов в продольном направлении и 10 рядов – в поперечном).
3. Результаты численного моделирования
Два режима возбуждения ДОС. Для анализа работы излучателя рассмотрим два режима работы: при возбуждении центрального волновода, а также при возбуждении одного из соседних с ним волноводов. В соответствии с феноменологической теорией [2] требуемая ДН должна формироваться только при возбуждении широких волноводов (с большими постоянными распространения). К их числу относится центральный волновод.
Результаты численного моделирования исследуемой структуры с приведенными выше параметрами на частоте 8 ГГц в этих двух режимах представлены на рис.3,4.
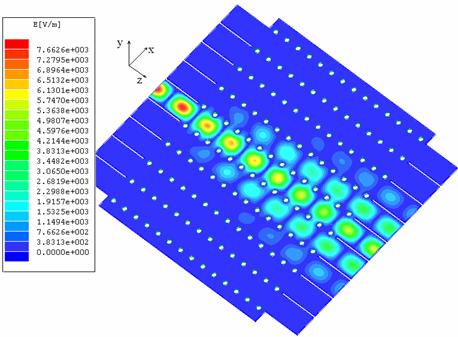
Рис.3. Распределение модуля электрического поля в плоскости XZ
при возбуждении широкого волновода.
На рис. 3 показано распределение электрического поля
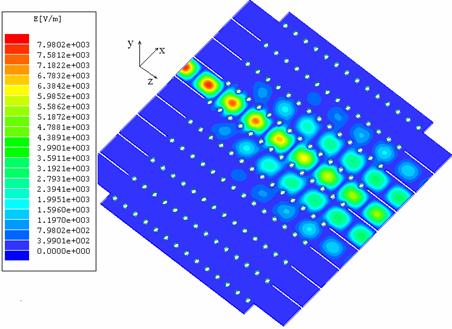
в плоскости XZ при возбуждении центрального канала, на рис. 4 – при возбуждении соседнего канала.
Рис.4. Распределение модуля электрического поля в плоскости XZ
при возбуждении узкого волновода.
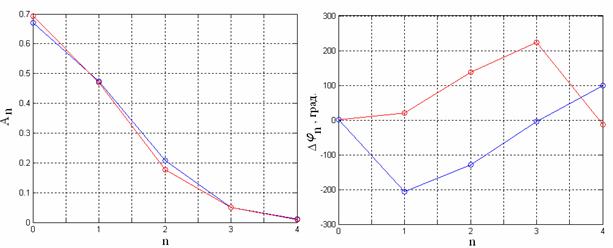
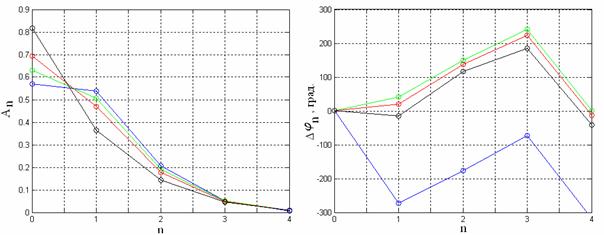
Из рисунков видно, что в обоих случаях при распространении волны вдоль структуры происходит перераспределение энергии поля между волноводными каналами. Рассмотрим представленные на рис. 5 распределения амплитуд и фаз волн в каналах ДОС в выходной апертуре. Здесь, и далее, каналы пронумерованы последовательно n=1,2,3,4, начиная от возбужденного, тогда как возбужденному каналу присваивается номер n=0. Как следует из рисунков, амплитудные распределения для указанных типов возбуждения практически совпадают (см. рис. 5,а), в то время как фазовые распределения существенно различаются (см. рис. 5,б). Вычисленные по формулам (1), (2) диаграммы направленности излучения в Н-плоскости, соответствующие приведенным распределениям амплитуды и фазы, изображены на рис. 6 (красная кривая соответствует активному каналу, синяя кривая – пассивному).
а) б)
Рис.5. Амплитудное и фазовое распределения при возбуждении активного (–––) и пассивного (–––) каналов.
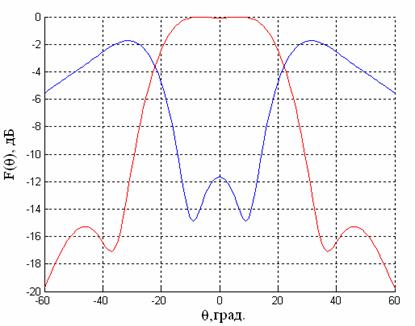
Рис.6. Диаграммы направленности излучателя при возбуждении активного (–––) и пассивного (–––) каналов.
Из рисунка видно, что при возбуждении центрального канала формируется ДН, форма которой близка к секторной. Это происходит благодаря тому, что амплитуда с увеличением номера канала (см. рис.5,а) быстро спадает, относительные фазы в нулевом, первом и четвертом каналах близки к значению 0°, а во втором и третьем канале – к 180 (см.рис.5,б), что и требуется для получении распределения близкого к
. При возбуждении пассивного канала первый канал имеет относительно нулевого фазовый сдвиг, близкий по значению к 180°, а амплитуды полей в них отличаются недостаточно сильно, в результате чего излучение вперед оказывается подавленным.
Оптимизация параметров EBG структуры. В исследуемой EBG структуре решетка цилиндров образует чередующиеся активные и пассивные волноводные каналы. Это обусловлено различными расстояниями между рядами цилиндров L1 и L2 (см. рис.1). Вид формируемого амплитудно-фазового распределения в такой структуре зависит от параметра
. Для определения оптимальной величины D при фиксированном периоде
а) б)
Рис.7. Амплитудное и фазовое распределения при различных значениях параметра D
(––– D=0 мм; ––– D=0.4 мм;––– D=0.6 мм; ––– D=0.8 мм)
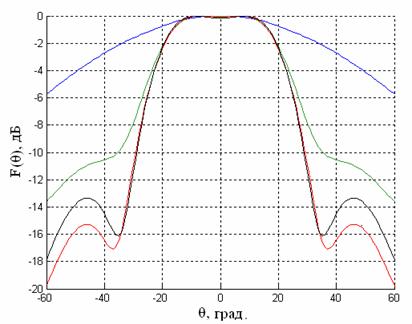
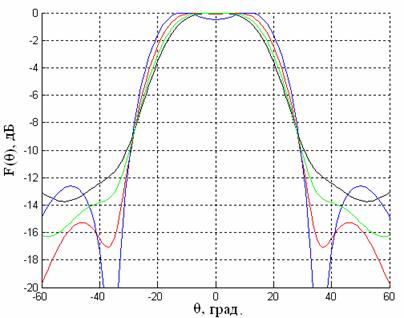
Рис.8. Диаграммы направленности в зависимости от параметра D
(––– D=0 мм; ––– D=0.4 мм;––– D=0.6 мм; ––– D=0.8 мм)
Из рис. 8 видно, что с увеличением параметра D ширина ДН уменьшается, форма ДН становится все ближе к секторной. Главные лепестки ДН при D=0,6 мм и 0,8 мм практически совпадают, однако при D=0,8 мм уровень бокового лепестка выше, чем в случае D=0,6 мм.
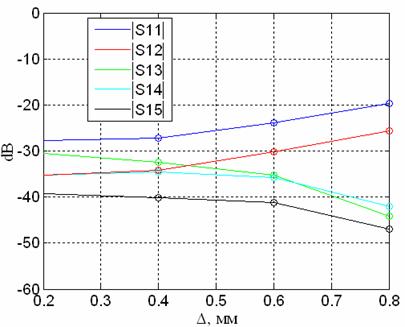
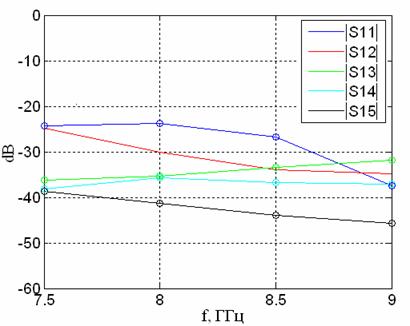
Рис.9. Коэффициенты отражения S 11 - S 15 в зависимости от параметра D.
Помимо формы ДН важными характеристиками при анализе свойств кластерного излучателя являются коэффициенты отражения. Результаты расчетов этих величин в зависимости от параметра D в диапазоне 8 ГГц представлены на рис.9. Как видно из рисунка, значения коэффициентов отражения в указанных пределах изменениях величины
не превышают –20 дБ, что говорит о хорошем согласовании и развязке входных каналов. Заметим, что величина
при D=0,8 мм на несколько дБ выше, чем в случае D=0,6 мм. Следовательно, принимая во внимание такие факторы, как форма ДН, уровень бокового излучения и уровень отражения целесообразно выбрать значение D=0,6 мм в качестве оптимального.
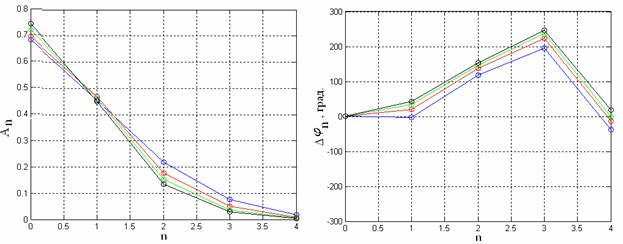
Диапазонные свойства ДОС. Для исследования частотных свойств кластерного излучателя проведено численное моделирование на частотах 7,5 ГГц; 8,0 ГГц; 8,5 ГГц; 9,0 ГГц при значении параметра D= 0,6 мм. Полученные семейства амплитудно-фазовых распределений приведены на рис.10. Диаграммы направленности, соответствующие этим распределениям, изображены на рис.11.
а) б)
Рис.10. Амплитудно-фазовые распределения в апертуре ДОС на разных частотах (––– 7,5ГГц; ––– 8,0ГГц; ––– 8,5ГГц; ––– 9,0 ГГц)
Рис.11. Диаграммы направленности в зависимости от частоты излучения
(––– 7,5ГГц; ––– 8,0ГГц; ––– 8,5ГГц; ––– 9,0 ГГц)
Следует заметить, что небольшие различия в амплитудно-фазовых распределениях (см. рис.10) в диапазоне исследуемых частот приводят к заметному изменению формы ДН (рис.11). Как видно из рисунка.11, ширина ДН на уровне -8 ..-10 дБ при изменении частоты в указанном диапазоне практически не изменяется. С ростом частоты расширяется плоский участок ДН, форма ДН приближается к секторной, но на частоте 9 ГГц наблюдается рост бокового лепестка. Уровень коэффициентов отражения, как показано на рис.12, во всем диапазоне от 7,5 до 9 ГГц не превышает –23 дБ.
Рис.12. Зависимости модулей коэффициентов отражения S 11 - S 15 от частоты.
4. Экспериментальное исследование
Для измерения характеристик кластера и проверки результатов численного моделирования был создан макет, внешний вид которого представлен на рис. 13,а-в. В макете EBG структура содержит в продольном направлении 14 рядов цилиндров с периодом 14 мм. В поперечном направлении период решётки составляет 50 мм, при этом размеры активных и пассивных каналов 25,6 мм и 24,4 мм, соответственно. Как показал анализ амплитудно-фазовых распределений, каждому активному каналу для формирования неискаженной ДН необходимо иметь, по крайней мере, 3 соседних канала с каждой стороны (апертура кластера должна состоять из 7 каналов). Из этих соображений число рядов в поперечном направлении структуры выбрано N=13, что позволяет сформировать 3 активных канала.
а)
б) в)
Рис.13. Фотографии макета кластерного излучателя.
На входе структуры имеется фланцы для присоединения возбуждающих волноводов. На выходе кластера плоский волновод, образованный двумя металлическими плоскостями, переходит в Е-плоскости в рупор (см. рис.13,б) с вертикальным размером b=56 мм. Размеры рупора выбраны из условия равенства ширины ДН кластера в Е- и Н-плоскостях на уровне –10 дБ.
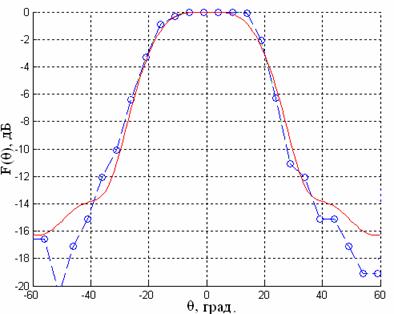
Измерения ДН макета кластерного излучателя были проведены на трех частотах: 7.815, 8.0, 8.5 ГГц. Результаты измерений представлены, соответственно, на рис.14-16 в сравнении с данными, полученными при численном моделировании в этих частотных диапазонах.
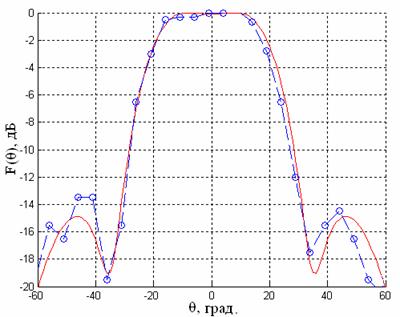
Рис.14 Диаграмма направленности кластерного излучателя
на частоте 7,815 ГГц
(–––– результаты моделирования, – – о – – данные эксперимента)
Рис.15 Диаграмма направленности кластерного излучателя
на частоте 8,0 ГГц
(–––– результаты моделирования, – – о – – данные эксперимента)
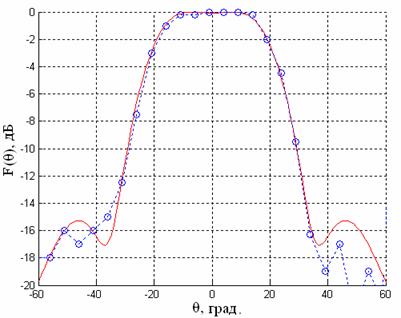
Рис. 16. Диаграмма направленности кластерного излучателя
на частоте 8,5 ГГц
(–––– результаты моделирования, – – о – – данные эксперимента)
Как следует из рисунков, результаты численного и физического экспериментов хорошо согласуются.
5. Заключение
В результате численного моделирования кластерного облучателя на основе планарной EBG структуры найдены амплитудно-фазовые распределения на выходе, ДН элемента решетки, выбраны оптимальные параметры и исследованы частотные свойства излучения. Создан макет кластерного облучателя и проведены измерения ДН излучения кластера на трех частотах. Результаты измерений сопоставлены с данными, полученными при численном моделировании.
Работа выполнена при поддержке РФФИ (грант 08-08-12200-офи)
СПИСОК ИСПОЛЬЗОВННЫХ ИСТОЧНИКОВ
1. В.А. Калошин, С.Е. Банков, Е.В.Фролова, Инновации в радиотехнических информационно-коммуникационных технологиях, Ч.2., М., «Экстра-Принт», , 2006 г., С.261-265.
2. Банков С.Е. // РЭ. 2009. Т. В печати.
3. Банков С.Е. Собственные волны волновода в двумерном фотонном кристалле из металлических цилиндров // РЭ. 2006. Т.51. №5. С. 533.
4. Скобелев С. П. Анализ и синтез антенной решетки с секторными парциальными диаграммами направленности // Радиотехника. 1990. № 10. С. 44.
,
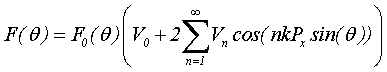(1) 
,
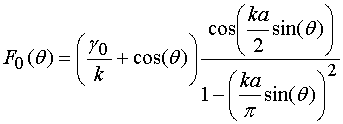(2)
