УДК 519.6
ПРИМЕНЕНИЕ ПОЛИФАЗНОГО РАЗЛОЖЕНИЯ ДЛЯ ЭФФЕКТИВНОЙ ВЫЧИСЛИТЕЛЬНОЙ РЕАЛИЗАЦИИ АЛГОРИТМА ФОРМИРОВАНИЯ СИГНАЛА НА ОСНОВЕ КОНЕЧНОМЕРНОГО ОБОБЩЕННОГО БАЗИСА ВЕЙЛЯ-ГЕЙЗЕНБРГА
Д. А. Петров, А. Н. Боголюбов
физический факультет МГУ имени М.В. Ломоносова, кафедра математики
Получена 9 марта 2010 г.
Аннотация. В работе вводится z-преобразование, которое затем используется при рассмотрении прореживающих, интерполирующих фильтров и банка равномерных ДПФ фильтров, лежащего в основе классических OFDM систем (систем с ортогональным частотным мультиплексированием). Рассмотрено, как полифазное разложение позволяет получить эффективную реализацию таких схем. OFTDM сигналы (с ортогональным частотно-временным уплотнением), формируемые на основе обобщенного базиса Вейля-Гейзенберга (WH), обладают значительно более высокой устойчивостью к межканальной интерференции (МКИ). Однако оцениваемый в статье объем вычислений, требующийся для их обработки, превосходит аналогичные показатели для классической схемы. В работе показано, что полифазное разложение позволяет значительно снизить объем вычислений в алгоритме формирования OFTDM-сигнала на основе WH‑базиса и построить эффективную схему модуляции.
Ключевые слова: базис Вейля-Гейзенберга, полифазное разложение, модуляция сигнала, OFTDM.
Введение
Значительный технологический прогресс, достигнутый в разработке новых алгоритмов передачи информации и их активном применении на практике, делает особенно актуальными исследования новых методов синтеза сигналов все более и более сложной структуры, обладающих оптимальными временно-частотными характеристиками. В настоящее время в системах связи 3G и 4G, цифровом телевидении (DVB) наиболее распространенной технологией передачи данных является мультиплексирование (уплотнение) с ортогональным частотным разделением (OFDM - Orthogonal Frequency Division Multiplexing). Структура и свойства OFDM сигнала определяются классическим базисом Вейля-Гейзенберга, на основе которого он формируется, как некоторая линейная комбинация базисных функций [1], [2]. Данный базис можно получить путем равномерных сдвигов по частоте прямоугольного формирующего импульса в пределах заданной полосы частот. С точки зрения обработки сигнала одним из основных преимуществ OFDM заключается в том, что процедура модуляции и демодуляции фактически сводится к обратному и прямому дискретным преобразованиям Фурье (ДПФ). Для ДПФ существует так называемые «быстрые» алгоритмы (БПФ), что позволяет сократить объем вычислений.
При построении беспроводных высокоскоростных цифровых систем связи часто возникает ситуация, когда реальный радиоканал (среда распространения) обладает частотно-временным рассеянием. Последнее обычно вызвано тем, что сигнал в точку приема приходит многочисленными путями после многократных отражений от нестационарных неоднородностей среды (городские постройки, движущиеся предметы, гидрометеоры, слои ионосферы и др.). В результате действия указанных факторов разрушается структура сигнала и на приемной стороне возникают помехи в виде межсимвольной и межканальной интерференции (МСИ и МКИ). Причем природа этих помех такова, что их нельзя скомпенсировать или отфильтровать обычными методами цифровой обработки, а уровень помех зависит от структуры сигнального базиса.
Прямоугольная форма формирующего импульса, характерная для классических OFDM систем, не является оптимальной с точки зрения устойчивости к межканальной интерференции (МКИ). Поскольку в этом случае локализация формируемых на основе неё базисных функций в частотной области будет наихудшей. По этой же причине в таких OFDM системах уровень внеполосного излучения оказывается завышенным. В литературе [3], [4] был предложен ряд подходов к подавлению МКИ. Однако эти методы приводят либо к весьма значительной потере спектральной и энергетической эффективности, либо к нарушению ортогональности. Таким образом, задача борьбы с межканальной интерференцией в мобильных OFDM системах является очень актуальной, и во многих случаях пока не находит удовлетворительного решения.
В качестве основного метода борьбы с частотно-временным рассеянием (ЧВР) сигнала мы применяем специальные ортогональные хорошо-локализованные сигнальные базисы (обобщенные базисы Вейля-Гейзенберга), минимизирующие уровень взаимного влияния поднесущих каналов, как в частотной, так и во временной областях, но при этом не ухудшающих спектральную эффективность системы [5]-[8]. Сигнал, который строится на их основе называется OFTDM (сигнал с ортогональным частотно-временным уплотнением).
В современных цифровых системах количество базисных функций может достигать нескольких десятков тысяч, причем прием сигнала должен осуществляется компактными абонентскими устройствами. Соответственно, особую актуальность приобретает решаемая в статье задача разработки вычислительно эффективного алгоритма синтеза сигнала. Для его построения необходимо сначала рассмотреть такие методы, как z-преобразование и полифазное разложении и их применение в теории цифровой связи на примере более простых схем и устройств.
Полифазное разложение и Z-преобразование
Полифазное разложение последовательности состоит в
представлении ее как суперпозиции ![]() последовательностей,
каждая из которых состоит из всех кратных
последовательностей,
каждая из которых состоит из всех кратных ![]() значений подходящим образом
сдвинутой версии исходной последовательности [9], [10]. Применение такого
разложения к дискретной функции (импульсной характеристике фильтра) приводит к
эффективной реализации структур линейных фильтров.
значений подходящим образом
сдвинутой версии исходной последовательности [9], [10]. Применение такого
разложения к дискретной функции (импульсной характеристике фильтра) приводит к
эффективной реализации структур линейных фильтров.
Линейные инвариантные по времени системы
характеризуются импульсной передаточной функцией, или импульсной
характеристикой. Рассмотрим импульсную характеристику ![]() ,
и разложим ее на
,
и разложим ее на ![]() последовательностей
последовательностей ![]() ,
, ![]() :
:

Сдвинув надлежащим образом составные части, можно восстановить исходную последовательность:
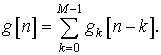
Последовательности
![]() (1)
(1)
называются полифазными
компонентами функции ![]() .
.
Полифазное разложение лежит в основе возможности
разложения фильтра на ![]() параллельных фильтров. Одно из
важных приложений полифазного разложения –эффективная реализация фильтров, чьи
отклики в дальнейшем подвергаются понижающей или повышающей дискретизации.
параллельных фильтров. Одно из
важных приложений полифазного разложения –эффективная реализация фильтров, чьи
отклики в дальнейшем подвергаются понижающей или повышающей дискретизации.
Z-преобразование дискретных сигналов является аналогом преобразования Лапласа непрерывных сигналов. Кроме того, эти преобразования имеют схожую связь с преобразованием Фурье.
Z-преобразование дискретной
последовательности ![]() вводится соотношением:
вводится соотношением:
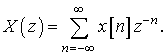 (2)
(2)
Правая часть этой формулы – бесконечный степенной ряд от
комплексной переменной ![]() (ряд Лорана). Соответствие
между последовательностью и ее z-преобразованием
обозначается как
(ряд Лорана). Соответствие
между последовательностью и ее z-преобразованием
обозначается как
![]()
Заменяя комплексную переменную ![]() в формуле на
в формуле на ![]() , мы сводим z‑преобразование
к преобразованию Фурье.
, мы сводим z‑преобразование
к преобразованию Фурье.
Z-преобразование обладает свойством задержки, согласно которому

Еще одним важным свойством z-преобразования является то, что z-преобразование реакции линейной стационарной системы на поданный сигнал является произведением z‑преобразований самого сигнала и импульсной характеристики системы, т.е. согласно формуле свертки:
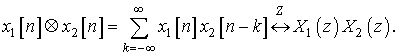
Рассмотрим фильтр, имеющий z-преобразование
импульсной характеристики 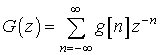 , называемое
передаточной функцией. В частном случае когда
, называемое
передаточной функцией. В частном случае когда ![]() ,
, ![]() называется частотной характеристикой, а
её модуль
называется частотной характеристикой, а
её модуль ![]() амплитудно-частотной характеристикой
(АЧХ).
амплитудно-частотной характеристикой
(АЧХ).
В качестве примера разделим ![]() на
элементы с четными и нечетными номерами, тогда
на
элементы с четными и нечетными номерами, тогда
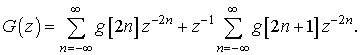
Определив
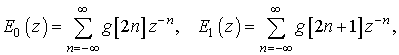
![]() можно
переписать в виде
можно
переписать в виде
![]()
В общем же случае, ![]() можно
разложить на
можно
разложить на ![]() компонент:
компонент:
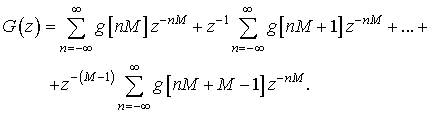
В более компактной форме это выражение можно переписать в виде
где ![]() -
полифазные компоненты
-
полифазные компоненты ![]() , определяемые .
, определяемые .
На
практике часто приходится сталкиваться с тем, что в результате дискретизации непрерывной функции (![]() ) вместо дискретной функции
) вместо дискретной функции ![]() ,
, ![]() известны только ее значения
известны только ее значения ![]() на
конечном множестве точек
на
конечном множестве точек ![]() . По этой причине используются
. По этой причине используются ![]() ‑периодические
функций
‑периодические
функций ![]() , определенные для всех
, определенные для всех ![]() . Причем, для
. Причем, для ![]()
![]() . Это пространство имеет размерность
. Это пространство имеет размерность ![]() и является евклидовым , если ввести скалярное произведение
любых двух
и является евклидовым , если ввести скалярное произведение
любых двух ![]() -периодических функций
-периодических функций ![]() следующим образом:
следующим образом:
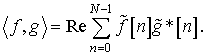 (4)
(4)
Введем аналоги рассмотренных выше преобразований в
конечномерном пространстве ![]() . Для этого рассмотрим
конечную последовательность
. Для этого рассмотрим
конечную последовательность ![]() , причем
, причем ![]() . Если эта последовательность будет
выступать в качестве импульсной характеристики фильтра, то он будет называться
фильтром с конечно импульсной характеристикой (КИХ фильтром). Разложим
. Если эта последовательность будет
выступать в качестве импульсной характеристики фильтра, то он будет называться
фильтром с конечно импульсной характеристикой (КИХ фильтром). Разложим ![]() на
на ![]() подпоследовательностей
подпоследовательностей
![]()
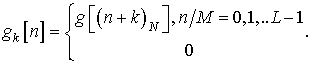
Исходную последовательность можно выразить следующим образом:
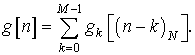
Тогда ![]() будут
играть роль полифазных компонент.
будут
играть роль полифазных компонент.
Введем конечномерный аналог z-преобразования:
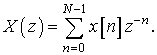
Если ![]() , то выполняется свойство задержки:
, то выполняется свойство задержки:

В общем случае ![]() полифазных компонент
полифазных компонент
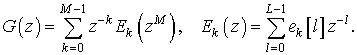 (5)
(5)
Прореживающие и интерполирующие фильтры, тождества Нобеля
Одной из причин, почему параллельная (multirate) обработка сигналов завоевала большую популярность является изобретение полифазного разложения (Bellanger, 22, 1976, Vary, 1979). Это позволило выполнять вычисления на наиболее низкой частоте и снизило требования к скорости работы процессоров. Полифазное разложение необходимо практически во всех приложениях параллельной обработки сигналов и в подавляющем большинстве случаев приводит к значительному повышению вычислительной эффективности. Полифазное разложение играет важную роль в теоретических исследованиях, при разработке устройств и банков фильтров.
Наиболее распространенными операциями в параллельной цифровой теории обработки сигналов является прореживание (понижение частотны дискретизации) и интерполяция (повышение частоты дискретизации).
![]() -кратный прореживатель,
на вход которого поступает последовательность
-кратный прореживатель,
на вход которого поступает последовательность ![]() на
выходе имеет
на
выходе имеет ![]() где
где ![]() -
целое число. Только те отсчеты, которые соответствуют моментам времени, кратным
-
целое число. Только те отсчеты, которые соответствуют моментам времени, кратным
![]() , пропускаются устройством.
, пропускаются устройством.
![]() -кратный интерполятор
действует таким образом, что если на вход этого устройства подается
последовательность
-кратный интерполятор
действует таким образом, что если на вход этого устройства подается
последовательность ![]() , то на выходе будет наблюдаться
сигнал
, то на выходе будет наблюдаться
сигнал
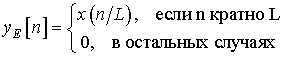
Проанализируем работу этих устройств в z-представлении:

Таким образом, ![]() . Это
означает, что
. Это
означает, что ![]() представляет сжатую в L раз
версию
представляет сжатую в L раз
версию ![]() .
.
Для ![]() -кратного прореживателя
справедливо аналогичное соотношение. Для его получения рассмотрим
z-преобразование
-кратного прореживателя
справедливо аналогичное соотношение. Для его получения рассмотрим
z-преобразование ![]() :
:

Определим вспомогательную последовательность
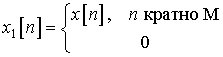
таким образом, что ![]() . Тогда
. Тогда

Это выражение справедливо, т.к. ![]() равно
нулю для всех
равно
нулю для всех ![]() , не кратных
, не кратных ![]() . Поэтому
. Поэтому
![]() (6)
(6)

Причем последовательность ![]() можно
представить в виде
можно
представить в виде

где ![]() .
.
Таким образом,
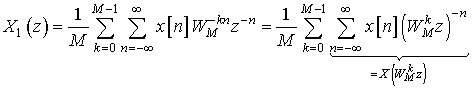
Теперь из (6) непосредственно следует, что
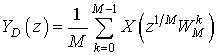 (7)
(7)
Если положить ![]() , то соотношение приобретет вид
, то соотношение приобретет вид
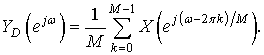
В большинстве приложений прореживателю предшествует низкочастотный фильтр. Это гарантирует ограниченность по частоте сигнала, частота дискретизации которого понижается. Системы, в которых прореживатель или интерполятор последовательно комбинируется с фильтром, называются прореживающим и интерполирующим фильтром, соответственно.
Во временной области сигналы на входе/выходе прореживающих и интерполирующих фильтров связаны соотношениями:
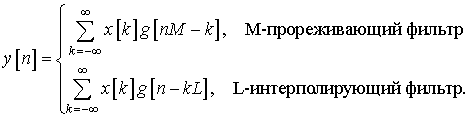 (8)
(8)
Для прореживающего фильтра это соотношение также может быть записано в виде:
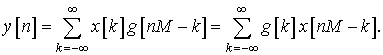
При применении полифазного разложения к
прореживающим и интеполирующим фильтрам что возникают схемы изображенные на
рис. 1(a) (фильтр ![]() следует
за прореживателем) и рис. 1(c) (фильтр
следует
за прореживателем) и рис. 1(c) (фильтр ![]() следует перед интерполятором). Можно
показать, что схемы (a), (с) оказываются эквивалентными
схемам (b) и (d). Тождества,
устанавливающие их эквивалентность, называются тождествами
Нобеля.
следует перед интерполятором). Можно
показать, что схемы (a), (с) оказываются эквивалентными
схемам (b) и (d). Тождества,
устанавливающие их эквивалентность, называются тождествами
Нобеля.
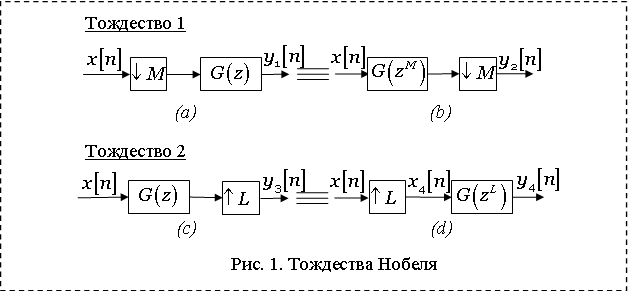
В том случае, если ![]() является
рациональной функцией (например, степень полинома
является
рациональной функцией (например, степень полинома ![]() или
или ![]() ), то указанный фильтр и операция
понижении (повышения) частоты дискретизации можно поменять местами.
), то указанный фильтр и операция
понижении (повышения) частоты дискретизации можно поменять местами.
Сначала докажем, что эти тождества могут не
выполняться для иррациональных ![]() (например,
(например, ![]() ). Рассмотрим систему (a).
Если бы тождества выполнялись, то эту систему можно было бы представить в виде
(b). Легко проверить, что эти системы не эквиваленты. Например, если
последовательность
). Рассмотрим систему (a).
Если бы тождества выполнялись, то эту систему можно было бы представить в виде
(b). Легко проверить, что эти системы не эквиваленты. Например, если
последовательность ![]() такая, что
такая, что ![]() для всех
для всех ![]() , то
, то ![]() должна равняться нулю для всех
должна равняться нулю для всех ![]() , но для
, но для ![]() это не
обязательно так.
это не
обязательно так.
Для того чтобы доказать первое тождество в случае
рациональных ![]() , заметим, что
, заметим, что
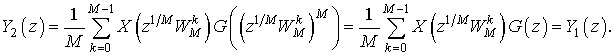
Для второго тождества:
![]()
Рассмотрим теперь, как полученные результаты можно применить к более сложной системе, представляющей собой банк фильтров.
Банк ДПФ фильтров
Банк цифровых фильтров представляет собой набор фильтров с общим выходом или общим входом. Различают анализирующий банк фильтров, имеющих один вход и состоящий из набора анализирующих фильтров, и синтезирующий банк фильтров, который объединяет набор входящих последовательностей в один сигнал.
Рассмотрим ДПФ банк фильтров на основе матрицы
![]() . ДПФ матрица
. ДПФ матрица ![]() размерности
размерности
![]() имеет элементы
имеет элементы ![]() ,
где
,
где ![]() . Матрица
. Матрица ![]() является
ортогональной, т.е.
является
ортогональной, т.е. ![]() , где
, где ![]() означает
эрмитово сопряжение, и симметричной, т.е.
означает
эрмитово сопряжение, и симметричной, т.е. ![]() . Если
задана конечная последовательность
. Если
задана конечная последовательность ![]() ,
, ![]() то определив вектор
то определив вектор ![]() , ДПФ последовательности
, ДПФ последовательности ![]() можно записать в виде
можно записать в виде ![]() , а обратное ДПФ в виде
, а обратное ДПФ в виде ![]() .
.
На вход системы (рис. 2) подается последовательность
![]() . В результате прохождения
. В результате прохождения ![]() через каскад задержки, на основе этой последовательности
генерируется
через каскад задержки, на основе этой последовательности
генерируется ![]() подпоследовательностей
подпоследовательностей ![]() , каждая из которых подвергается обратному
ДПФ (с точностью до нормирующего множителя
, каждая из которых подвергается обратному
ДПФ (с точностью до нормирующего множителя ![]() ):
):
 (9)
(9)

Другими словами, для любого значения временного
индекса ![]() рассчитывается набор из
рассчитывается набор из ![]() сигналов
сигналов ![]() на
основе набора
на
основе набора ![]() сигналов
сигналов ![]() в соответствии с формулой . Соотношение можно переписать в виде:
в соответствии с формулой . Соотношение можно переписать в виде:

Таким образом, можно записать, что ![]() где
где
![]() (10)
(10)
причем ![]()
Т.е. система эквивалентна банку фильтров, состоящему
из анализирующих КИХ фильтров ![]() . Заметим, что АЧХ
фильтра
. Заметим, что АЧХ
фильтра ![]() имеет вид
имеет вид ![]() , а
частотная характеристика фильтра
, а
частотная характеристика фильтра ![]() :
:
![]()
представляет собой
сдвинутую по частоте версию ![]() . Т.е. мы имеем банк из
. Т.е. мы имеем банк из
![]() фильтров, представляющих собой
равномерные сдвиги
фильтров, представляющих собой
равномерные сдвиги ![]() .
.
Банки фильтров, в которых фильтры связаны
соотношением вида называются ДПФ банками фильтров. Чтобы объяснить физический
смысл сигналов ![]() , наблюдающихся на выходе анализирующих
фильтров, рассмотрим последовательности
, наблюдающихся на выходе анализирующих
фильтров, рассмотрим последовательности
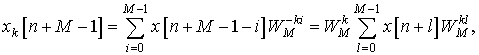
где учтено, что ![]() и
и ![]() .
Поэтому
.
Поэтому ![]() равняется
равняется ![]() , умноженному на
, умноженному на ![]() -ую точку ДПФ
-ую точку ДПФ ![]() -точечной
последовательности
-точечной
последовательности
![]()
Эта последовательность представляет собой ничто
иное, как ![]() -точечный сегмент последовательности
-точечный сегмент последовательности ![]() , начинающийся с точки
, начинающийся с точки ![]() . Т.о. значение
. Т.о. значение ![]() отвечает
значению (
отвечает
значению (![]() -ой точке) ДПФ последовательности . С течением времени (с увеличением
-ой точке) ДПФ последовательности . С течением времени (с увеличением ![]() ) это значение обновляется, т.е.
пересчитывается для следующего сегмента из
) это значение обновляется, т.е.
пересчитывается для следующего сегмента из ![]() отсчетов.
отсчетов.
Рассмотренный банк фильтров представляет собой
спектральный анализатор. ![]() -ый выход
-ый выход ![]() фактически является спектром (
фактически является спектром (![]() -ой точкой ДПФ с точностью до
масштабирующего коэффициента
-ой точкой ДПФ с точностью до
масштабирующего коэффициента ![]() ), рассчитанным на
основе последних
), рассчитанным на
основе последних ![]() точек последовательности
точек последовательности ![]() . Так как
. Так как ![]() является
выходом фильтра с частотной характеристикой
является
выходом фильтра с частотной характеристикой ![]() , то
он в основном представляет часть спектра
, то
он в основном представляет часть спектра ![]() в
окрестности частоты
в
окрестности частоты ![]() . В реальности
. В реальности ![]() соответствует некоторой усредненной
версии точного спектра
соответствует некоторой усредненной
версии точного спектра ![]() на этой частоте, т.к.
фильтр пропускает не одну частоту, а некоторую полосу частот. Разрешение
спектрального анализатора может быть улучшено, если увеличить дину фильтров
на этой частоте, т.к.
фильтр пропускает не одну частоту, а некоторую полосу частот. Разрешение
спектрального анализатора может быть улучшено, если увеличить дину фильтров ![]() . В любом случае, тот факт, что частотные
характеристики фильтров являются пересекающимися, приводит к тому, что
. В любом случае, тот факт, что частотные
характеристики фильтров являются пересекающимися, приводит к тому, что ![]() представляет собой некоторый усредненный
эффект в окрестности частоты
представляет собой некоторый усредненный
эффект в окрестности частоты ![]() .
.
Если же мы рассмотрим фильтр-прототип ![]() более высокого порядка с более резким
границами АЧХ, то сдвинутые версии будут иметь более низкий уровень перекрытия.
Позднее в работе будет показано, что ДПФ банк фильтров может быть модифицирован
таким образом, что
более высокого порядка с более резким
границами АЧХ, то сдвинутые версии будут иметь более низкий уровень перекрытия.
Позднее в работе будет показано, что ДПФ банк фильтров может быть модифицирован
таким образом, что ![]() фильтров будут задействоваться
(применяться) по «цене» практически одного фильтра.
фильтров будут задействоваться
(применяться) по «цене» практически одного фильтра.
На практике ![]() может
быть умножена на некоторую оконную функцию, что позволяет снизить влияние
боковых лепестков частотной характеристики. С течением времени оконная функция,
сдвигается одновременно со смещением
может
быть умножена на некоторую оконную функцию, что позволяет снизить влияние
боковых лепестков частотной характеристики. С течением времени оконная функция,
сдвигается одновременно со смещением ![]() -точечного сегмента . Это позволяет лучше локализовать данные в частотной области перед расчетом преобразования
Фурье.
-точечного сегмента . Это позволяет лучше локализовать данные в частотной области перед расчетом преобразования
Фурье.
Этот механизм со сдвигающей оконной функцией лежит в основе идеи о кратковременном (или оконном) преобразовании Фурье. Кроме того, в рассмотренном случае, уже фактически используется оконная прямоугольная функции, как и в классическом варианте технологии OFDM.
Эффективная структура прореживающих и интерполирующих фильтров
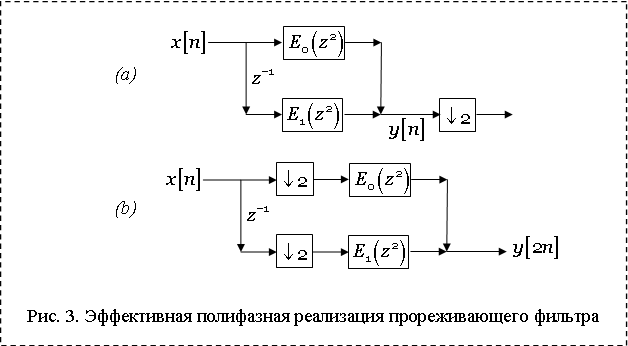
Рассмотрим прореживающий фильтр в случае ![]() . Если мы представим
. Если мы представим ![]() в виде суперпозиции двух полифазных
компонент
в виде суперпозиции двух полифазных
компонент ![]() , то систему можно представить в виде
схемы, изображенной на рис. 3(a). Если же дополнительно применить 1-ое тождество
Нобеля, то получим схему, изображенную на рис. 3(b).
, то систему можно представить в виде
схемы, изображенной на рис. 3(a). Если же дополнительно применить 1-ое тождество
Нобеля, то получим схему, изображенную на рис. 3(b).
Последняя реализация является более эффективной,
чем прямое использование фильтра ![]() .
.
Пусть ![]() является фильтром с
конечной импульсной характеристикой (КИХ фильтром)
является фильтром с
конечной импульсной характеристикой (КИХ фильтром) ![]() -ого
порядка. Традиционная схема прореживающего фильтра на его основе изображена на
рис. 4:
-ого
порядка. Традиционная схема прореживающего фильтра на его основе изображена на
рис. 4:
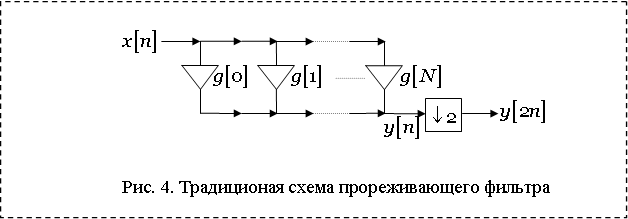
На выходе системы (рис. 4) используются только
четные отсчеты ![]() . Расчет состоит из
. Расчет состоит из ![]() умножений и
умножений и ![]() сложений.
При изменении времени от
сложений.
При изменении времени от ![]() к
к ![]() сигнал, сохраненный в каскаде замедления,
меняется (сдвигается), поэтому указанные вычисления должны проводиться один раз
в единицу времени, т.е. скорость выполнения операций составляет
сигнал, сохраненный в каскаде замедления,
меняется (сдвигается), поэтому указанные вычисления должны проводиться один раз
в единицу времени, т.е. скорость выполнения операций составляет ![]() умножений и
умножений и ![]() сложений
в единицу времени. Однако, для нечетных отсчетов сигнал на выходе не должен изменяться,
поэтому вычислительные ресурсы фактически используются неэффективно.
сложений
в единицу времени. Однако, для нечетных отсчетов сигнал на выходе не должен изменяться,
поэтому вычислительные ресурсы фактически используются неэффективно.
Теперь обратимся к полифазной реализации (рис. 3(b)).
Пусть ![]() и
и ![]() -
порядок фильтров
-
порядок фильтров ![]() и
и ![]() ,
, ![]() . Таким образом, для
. Таким образом, для ![]() требуется
требуется ![]() умножений
и
умножений
и ![]() сложений (
сложений (![]() ). И
хотя общий объем вычислений не изменяется: с учетом дополнительного сумматора
опять требуется
). И
хотя общий объем вычислений не изменяется: с учетом дополнительного сумматора
опять требуется ![]() умножений и
умножений и ![]() сложений. Но при этом
сложений. Но при этом ![]() работают на более низкой частоте, поэтому
требуется
работают на более низкой частоте, поэтому
требуется ![]() умножений и
умножений и ![]() сложений
в единицу времени. Сумматорам и умножителям в фильтрах
сложений
в единицу времени. Сумматорам и умножителям в фильтрах ![]() и
и
![]() доступен двойной интервал времени для
выполнения операций, кроме того они равномерно загружены, т.е. отсутствует
«интервал простоя».
доступен двойной интервал времени для
выполнения операций, кроме того они равномерно загружены, т.е. отсутствует
«интервал простоя».
В общем случае, при разложении на ![]() полифазных компонент, объем вычислений в
единицу времени для каждого фильтра сокращается в
полифазных компонент, объем вычислений в
единицу времени для каждого фильтра сокращается в ![]() раз, т.е.
наблюдается эффект распараллеливания.
раз, т.е.
наблюдается эффект распараллеливания.
Полифазная реализация равномерного ДПФ банка фильтров
Полифазное разложение может быть использовано для того, чтобы реализовать равномерный ДПФ банк фильтров, рассмотренный ранее, очень эффективным образом.
![]() -ый фильтр ДПФ банка
может быть представлен в следующем виде (с учетом определения равномерного
фильтра и его представления в виде суперпозиции
-ый фильтр ДПФ банка
может быть представлен в следующем виде (с учетом определения равномерного
фильтра и его представления в виде суперпозиции ![]() полифазных
компонент):
полифазных
компонент):
где учтено, что ![]() . Выход
. Выход ![]() -ого
фильтра
-ого
фильтра ![]() имеет вид:
имеет вид:
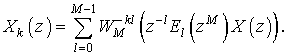
Отсюда следует, что вместо банка ![]() фильтров
фильтров ![]() может
быть использовано
может
быть использовано ![]() фильтров
фильтров ![]() и банк фильтров на основе ДПФ матрицы
(рис. 5).
и банк фильтров на основе ДПФ матрицы
(рис. 5).
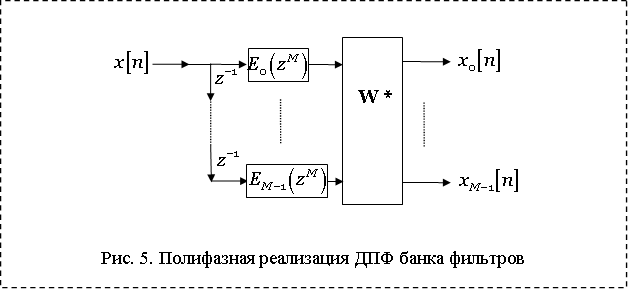
Преимущество такой системы заключается в том, что
мы можем использовать либо более длинный фильтр ![]() , но при
этом размер матрицы ДПФ остается тем же. Либо мы можем использовать
, но при
этом размер матрицы ДПФ остается тем же. Либо мы можем использовать ![]() той же длины, но при этом размер ДПФ
матрицы уменьшается.
той же длины, но при этом размер ДПФ
матрицы уменьшается.
Если ![]() является КИХ фильтром
порядка
является КИХ фильтром
порядка ![]() , то требуется
, то требуется ![]() умножений
и
умножений
и ![]() сложений для полифазных компонент.
Прибавив к этому затраты на вычисление ДПФ, получим полный объем вычислений.
сложений для полифазных компонент.
Прибавив к этому затраты на вычисление ДПФ, получим полный объем вычислений.
Если все ![]() , то мы,
конечно, получим стандартную схему ДПФ банка фильтров (рис. 3). Однако
присутствие
, то мы,
конечно, получим стандартную схему ДПФ банка фильтров (рис. 3). Однако
присутствие ![]() позволяет использовать фильтр-прототип
позволяет использовать фильтр-прототип ![]() большей длины, поэтому прототип (и
соответственно все
большей длины, поэтому прототип (и
соответственно все ![]() параллельных фильтров) могут
иметь лучшую локализацию. Это позволяет интерпретировать банк фильтров, как
систему, рассчитывающую ДПФ со сдвигающимся «окном», но теперь окно обладает
большей длиной, хотя матрица ДПФ остается той же размерности, т.е.
параллельных фильтров) могут
иметь лучшую локализацию. Это позволяет интерпретировать банк фильтров, как
систему, рассчитывающую ДПФ со сдвигающимся «окном», но теперь окно обладает
большей длиной, хотя матрица ДПФ остается той же размерности, т.е. ![]() .
.
Для составных ![]() (например,
для
(например,
для ![]() ) могут быть использованы алгоритмы БПФ. Например,
если
) могут быть использованы алгоритмы БПФ. Например,
если ![]() ,
, ![]() .
Стандартный алгоритм БПФ требует около 136 умножений. Таким образом, общее
число умножений будет 136+51=187. Если бы каждый из 32 фильтров применялся
независимо, то число умножений составило бы
.
Стандартный алгоритм БПФ требует около 136 умножений. Таким образом, общее
число умножений будет 136+51=187. Если бы каждый из 32 фильтров применялся
независимо, то число умножений составило бы ![]() , что
почти в 9 раз больше. Более того, т.к. большинство фильтров
, что
почти в 9 раз больше. Более того, т.к. большинство фильтров ![]() имеют комплексные умножители, не смотря
на то, что
имеют комплексные умножители, не смотря
на то, что ![]() имеет действительные коэффициенты, то
объем вычислений еще больше. Таким образом, полифазная реализация действительно
очень эффективна.
имеет действительные коэффициенты, то
объем вычислений еще больше. Таким образом, полифазная реализация действительно
очень эффективна.
На практике часто требуется проредить выходы
фильтров ![]() в
в ![]() раз. Это логично, т.к. каждый из этих
выходных сигналов имеет частотный диапазон примерно в
раз. Это логично, т.к. каждый из этих
выходных сигналов имеет частотный диапазон примерно в ![]() раз
уже, чем у
раз
уже, чем у ![]() . Используя 1-ое тождество Нобеля,
полифазный ДПФ банк фильтров с прореживателями может быть построен, как
показано на рис. 6.
. Используя 1-ое тождество Нобеля,
полифазный ДПФ банк фильтров с прореживателями может быть построен, как
показано на рис. 6.
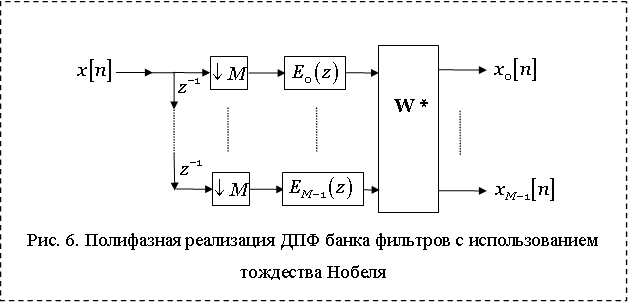
Для такой системы требуется в ![]() раз меньше операций в единицу времени,
поэтому реализация является еще более эффективной. В рассмотренном выше
примере, реальное количество умножений в единицу времени всего около 6. Другими
словами за 6 умножений в единицу времени мы используем 32 фильтра 50-ого
порядка.
раз меньше операций в единицу времени,
поэтому реализация является еще более эффективной. В рассмотренном выше
примере, реальное количество умножений в единицу времени всего около 6. Другими
словами за 6 умножений в единицу времени мы используем 32 фильтра 50-ого
порядка.
Далее рассмотрим, как инструментарий прореживающих, интерполирующих фильтров и полифазного разложения позволяет сформировать эффективный алгоритм и схему синтеза OFTDM сигнала.
Конечномерный обобщенный базис Вейля-Гейзенберга и формирование OFTDM сигнала
Передаваемый OFTDM сигнал в дискретном времени можно представить в виде [5]-[8]:
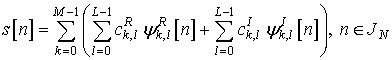
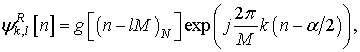
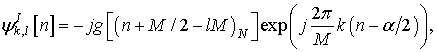
где ![]() ,
,
![]() - действительные и мнимые части
комплексных информационных QAM символов
- действительные и мнимые части
комплексных информационных QAM символов ![]() ,
, ![]() и
и ![]() -
комплексные функции, полученные в результате равномерных сдвигов по времени и
частоте двух инициализирующих функций
-
комплексные функции, полученные в результате равномерных сдвигов по времени и
частоте двух инициализирующих функций ![]() и
и ![]() ;
; ![]() -
количество поднесущих,
-
количество поднесущих, ![]() ;
; ![]() - фазовый параметр;
- фазовый параметр; ![]() - значение числа
- значение числа ![]() по модулю
по модулю ![]() . Система
базисных функций
. Система
базисных функций ![]() ортонормирована
на дискретном интервале
ортонормирована
на дискретном интервале ![]() в смысле вещественного
скалярного произведения , введенного в пространстве
в смысле вещественного
скалярного произведения , введенного в пространстве ![]() .
.
Конечномерный обобщенный базис Вейля-Гейзенберга ![]() можно представить в виде блочной
прямоугольной матрицы
можно представить в виде блочной
прямоугольной матрицы ![]() размерности
размерности ![]() , у которой блоки
, у которой блоки ![]() -
квадратные комплексные
-
квадратные комплексные ![]() матрицы, составленные для всех
матрицы, составленные для всех ![]() и
и ![]() из
столбцов базисных функций
из
столбцов базисных функций ![]() и
и ![]() , соответственно. Таким образом, матрицы
, соответственно. Таким образом, матрицы ![]() и
и ![]() состоят
из
состоят
из ![]() блоков по
блоков по ![]() столбцов,
а их элементы имеют вид:
столбцов,
а их элементы имеют вид:
![]()
В этом случае условие ортогональности базиса можно записать в виде:
![]()
где ![]() -
единичная диагональная матрица размерности
-
единичная диагональная матрица размерности ![]() .
.
Вместо комплексной матрицы ![]() можно
также рассматривать квадратную действительную матрицу размерности
можно
также рассматривать квадратную действительную матрицу размерности ![]()

Для синтеза сигнала (последовательности ![]() ) нужно умножить матрицу базиса
) нужно умножить матрицу базиса ![]() на вектор информационных символов
на вектор информационных символов ![]() :
:
![]()
Эта операция требует ![]() комплексных
сложений и
комплексных
сложений и ![]() комплексных умножений.
комплексных умножений.
Процесс демодуляции OFTDM сигнала имеет вид:
![]()
Представим эту операцию в матричном виде:
![]()
т.е. кроме такого же числа комплексных сложений и умножений, как для модуляции, требуется еще произвести операцию взятия реальной части вектора.
Кроме того, эти же операции можно реализовать и при
помощи действительной матрицы базиса ![]() :
:
![]()
Эта операция требует ![]() операций
действительного умножения и
операций
действительного умножения и ![]() сложений.
сложений.
Для получения процесса демодуляции представим
матрицу ![]() в виде блоков:
в виде блоков:

Кроме того, ![]() . Так нам требуется
только
. Так нам требуется
только ![]() , то процесс демодуляции имеет вид:
, то процесс демодуляции имеет вид:
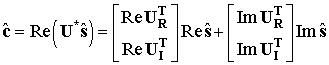
И требует, кроме выделения реальной и мнимой частей
сигнала ![]() ,
, ![]() действительных
умножений и
действительных
умножений и ![]() действительных сложений.
действительных сложений.
Т.о. в обоих случаях для проведения модуляции и
демодуляции требуется порядка ![]() операций, что,
конечно, значительно больше (даже в случае
операций, что,
конечно, значительно больше (даже в случае ![]() )
классической OFDM схемы, где объем вычислений составляет порядка
)
классической OFDM схемы, где объем вычислений составляет порядка ![]() .
.
Эффективная реализация алгоритма формирования сигнала на основе полифазного разложения и БПФ
Проведем ряд преобразований над выражением сигнала , чтобы получить его в форме, более удобной для дальнейшего использования. Т.к. количество
поднесущих ![]() является четным, то мы можем ввести
является четным, то мы можем ввести ![]() , тогда разбив на слагаемые с четным
, тогда разбив на слагаемые с четным ![]() и нечетным
и нечетным ![]() значением
значением
![]() получим
получим
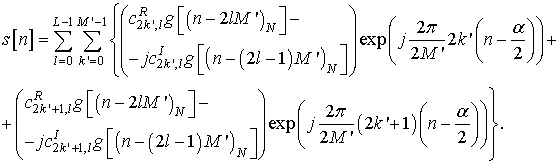
В первой строке суммы, если сдвиг ![]() по времени происходит на четное число
по времени происходит на четное число ![]() , то коэффициентом выступает
, то коэффициентом выступает ![]() , если же на нечетное, то -
, если же на нечетное, то - ![]() . Аналогично и во второй строке, т.е. для
четных сдвигов
. Аналогично и во второй строке, т.е. для
четных сдвигов ![]() - коэффициент
- коэффициент ![]() , для нечетны
, для нечетны ![]() -
- ![]() .
.
Эту запись сигнала можно представить в матричной форме:

где матрицы ![]() имеют размерность
имеют размерность ![]() ,
причем
,
причем ![]() соответствует
соответствует ![]() , в
которой отсутствуют все столбцы, отвечающие базисным функциям
, в
которой отсутствуют все столбцы, отвечающие базисным функциям ![]() с нечетными значениям индекса
с нечетными значениям индекса ![]() , а
, а ![]() -
четными значениями. Аналогично для
-
четными значениями. Аналогично для ![]() ,
, ![]() и
и ![]() .
Значит блочная матрица
.
Значит блочная матрица ![]() представляет собой
несколько реорганизованную форму записи базисной матрицы
представляет собой
несколько реорганизованную форму записи базисной матрицы ![]() . Векторы
. Векторы ![]() ,
, ![]() ,
, ![]() ,
, ![]() имеют длину
имеют длину ![]() и
состоят из информационных символов
и
состоят из информационных символов ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Для дальнейшего рассмотрения необходимо еще дополнительно преобразовать описанную выше блочную матрицу базиса Вейля-Гейзенберга. Пусть

Нетрудно проверить, что преобразования, соответствующие
приведенным матрицам, являются ортогональными, поэтому не приводят к изменению
ни свойств локализации, ни свойства ортонормированности базиса. В дальнейшем
будем пользоваться базисом, сформированным столбцами матрицы ![]() . При этом вместо сигнала
. При этом вместо сигнала ![]() будем формировать сигнал
будем формировать сигнал
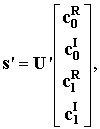
Более подробно сигнал ![]() может быть записан в виде:
может быть записан в виде:
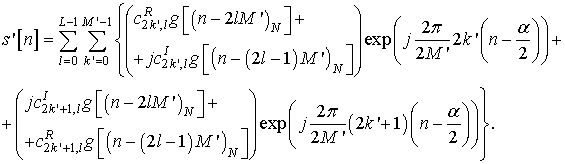
Введем новые обозначения:

Тогда
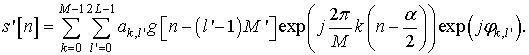
Действительно, если ![]() -
четное, а
-
четное, а ![]() -нечетное, то мы получим слагаемое
-нечетное, то мы получим слагаемое  ; если
; если ![]() -
четное и
-
четное и ![]() - четное, то слагаемое
- четное, то слагаемое  , аналогично, для двух оставшихся
слагаемых.
, аналогично, для двух оставшихся
слагаемых.
Семейство функций:
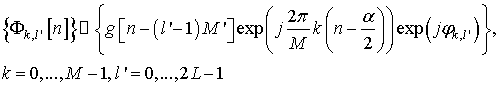
представляет собой модификацию
базиса Вейля-Гейзенберга ![]() , т.е. семейства
функции
, т.е. семейства
функции ![]() и
и ![]() фактически
совпадают с точностью до коэффициентов. Причем из ортогональности базиса
фактически
совпадают с точностью до коэффициентов. Причем из ортогональности базиса ![]() непосредственно следует ортогональность
семейства
непосредственно следует ортогональность
семейства ![]() :
:![]()
Это позволяет организовать процедуру синтеза сигнала следующим образом:
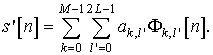
При этом разложение по базису (процедура демодуляции
сигнала) будет иметь вид (в предположении действительности ![]() )
)
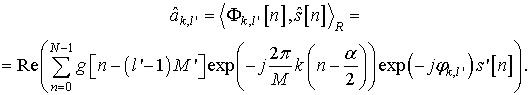
В случае передачи сигнала ![]() по
идеальному каналу без шумов, из непосредственно следует, что
по
идеальному каналу без шумов, из непосредственно следует, что ![]()
Выражение по форме близко к форме сигнала,
получаемого на выходе синтезирующего банка ![]() КИХ
КИХ ![]() -интерполирующих фильтров, который в
соответствии с имеет вид:
-интерполирующих фильтров, который в
соответствии с имеет вид:
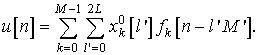
Непосредственной проверкой можно установить, что

При этом сигнал ![]() перепишем в виде:
перепишем в виде:
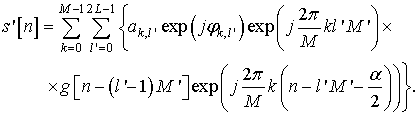
Тогда выражение совпадает с , если учесть и положить
![]()

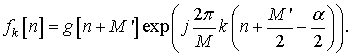
Преобразуем выражение с помощью z-преобразования:
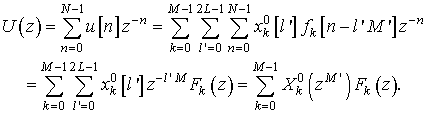
Воспользуемся аналогией с рассмотренным ранее ДПФ банком фильтров, где полифазное разложение, как было показано, позволяет использовать оконную функцию большей длины с сохранением размерности ДПФ матрицы. Для того чтобы получить эффективную реализацию такой системы необходимо использовать полифазное разложение, которое приводит к ОБПФ.
Полученный синтезирующий фильтр можно представить в
виде функций фильтра-прототипа ![]() . Его z-преобразование
имеет вид:
. Его z-преобразование
имеет вид:
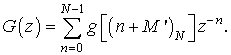
В соответствии с
(3) представим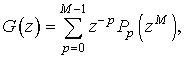

Получим z-представление фильтров ![]() через
через ![]() :
:
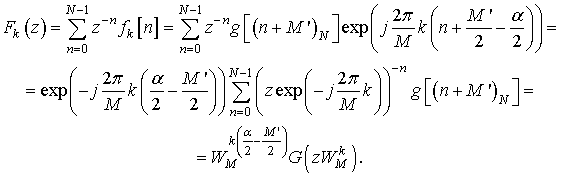
Это позволяет записать ![]() через
полифазные компоненты
через
полифазные компоненты ![]() и получить полифазную матрицу
и получить полифазную матрицу![]() :
:

Отсюда следует, что
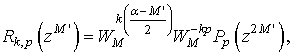
т.е.
![]()
где  ,
,
![]() ,
, ![]() .
.
Используя , выражение для ![]() можно записать в виде
можно записать в виде
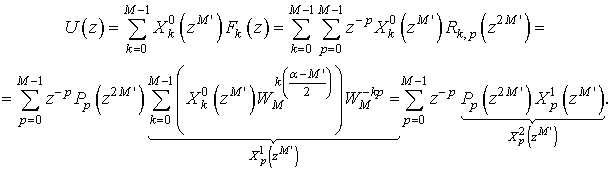
Функция ![]() в соответствии со
свойствами z-преобразования фактически представляет
собой свертку сигнала
в соответствии со
свойствами z-преобразования фактически представляет
собой свертку сигнала ![]() и импульсных характеристик
полифазных фильтров
и импульсных характеристик
полифазных фильтров ![]() .
.
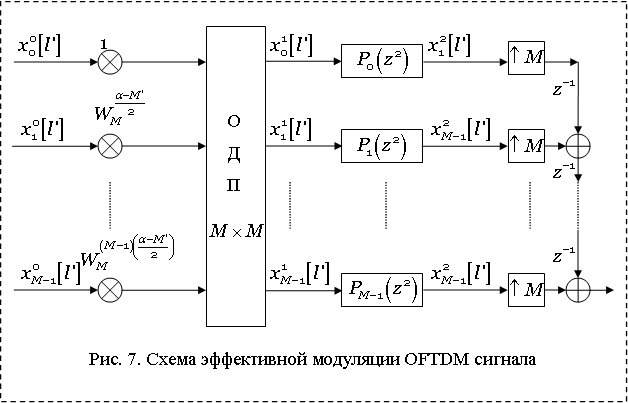
Кроме того, мы можем воспользоваться 1-ым тождеством
Нобеля и поставить ![]() интерполятор уже после
прохождения сигнала
интерполятор уже после
прохождения сигнала ![]() через фильтры
через фильтры ![]() (рис. 7), т.е. требуется рассчитать
свертку
(рис. 7), т.е. требуется рассчитать
свертку
![]()
Важно отметить, что первоначально фильтры ![]() имели длину
имели длину ![]() , но за
счет полифазного разложения удается использовать ОДПФ порядка
, но за
счет полифазного разложения удается использовать ОДПФ порядка ![]() и полифазные компонентами
и полифазные компонентами ![]() , соответствующие фильтру длиной
, соответствующие фильтру длиной ![]() .
.
|
Вычислительную эффективность алгоритма можно дополнительно улучшить. Для этого введем

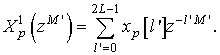
В работе [6] были найдены оптимальные с точки зрения
локализации значения фазового параметра, соответствующие двум типам симметрии
формирующей функции ![]() : случаю сопряженной
: случаю сопряженной ![]() -симметрии и случаю
-симметрии и случаю ![]() симметрии. Поэтому наибольший интерес
представляют именно эти значения
симметрии. Поэтому наибольший интерес
представляют именно эти значения ![]() . В случае
. В случае ![]()
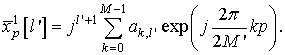
В случае ![]()
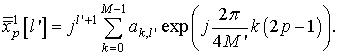
Таким образом, представляет собой ОДПФ действительной последовательности ![]() . В работе [11] показано, что это
преобразование может быть заменено на ОДПФ комплексной последовательности. При
этом объем вычислений сокращается, т.к. используется ДПФ матрица размерности
. В работе [11] показано, что это
преобразование может быть заменено на ОДПФ комплексной последовательности. При
этом объем вычислений сокращается, т.к. используется ДПФ матрица размерности ![]() .
.
Аналогично, также может быть рассчитано с помощью ОДПФ размерности ![]() комплексной последовательности.
комплексной последовательности.
В целом, в случае четного ![]() (наиболее
распространенный на практике случай) для произведения ОДПФ посредством БПФ
потребуется порядка
(наиболее
распространенный на практике случай) для произведения ОДПФ посредством БПФ
потребуется порядка ![]() операций.
операций.
Для вычисления свертки возьмем ![]() . Т.е. необходимо рассчитать ДПФ
последовательностей
. Т.е. необходимо рассчитать ДПФ
последовательностей ![]() , затем умножить их на ДПФ
последовательностей
, затем умножить их на ДПФ
последовательностей ![]() и произвести ОДПФ для получения
сигнала
и произвести ОДПФ для получения
сигнала ![]() , который затем подвергается
, который затем подвергается ![]() -интерполяции. Объем операций, необходимых
для проведения этих действий составит порядка
-интерполяции. Объем операций, необходимых
для проведения этих действий составит порядка ![]() .
.
В результате, общий объем вычислений составит порядка

что значительно меньше
полученной ранее оценки в ![]() . Кроме того, при
. Кроме того, при ![]() сложность алгоритма становится
сопоставимой с классической OFDM схемой.
сложность алгоритма становится
сопоставимой с классической OFDM схемой.
Проведенное исследование показывает, что предлагаемые методы и алгоритмы позволяют эффективно применять на практике хорошо локализованные базисы Вейля-Гейзенберга, обладающие высокой степенью локализации.
Литература
1. Прокис Дж., “Цифровая связь”, пер. с англ. / Под ред. Д.Д. Кловского, М.: Радио и связь, 2000 г.
2. W.Y. Zou, Y. Wu, “COFDM: An overview” // IEEE Trans. Broadc., March 1995, vol. 41, pp. 1-8.
3. R. Haas, J.C. Belfiore, «A time-frequency well-localized pulse for multiple carrier transmission» // Wireless Personal Communications, 1997, vol. 5, pp. 1-18.
4. C. Muschallik, «Improving an OFDM reception using an adaptive Nyquist windowing» // IEEE Transactions on Consumer Electronics, 1996, vol. 42, no. 3, pp. 259 – 269.
5. В.П. Волчков, «Сигнальные базисы с хорошей частотно-временной локализацией», журнал «Электросвязь», №2, С. 21-25, 2007.
6. В.П. Волчков, Д.А. Петров, «Оптимизация ортогонального базиса Вейля-Гейзенберга для цифровых систем связи, использующих принцип OFDM/OQAM передачи» // Научные ведомости БелГУ. Серия «История. Политология. Экономика. Информатика», 2009, №1(56), Вып. 9/1, С.102-110.
7. D.A. Petrov, V.P. Volchkov, “Orthogonal Well-Localized Weyl-Heisenberg Basis Construction and Optimization for Multicarrier Digital Communication Systems» // International Conference on Ultra Modern Telecommunications (ICUMT 2009), Oct 12-14, 2009, St. Petersburgh, Russia, ISBN: 978-1-4244-3941-6, IEEE Catalog Number: CFP0963G-CDR (http://ieeexplore.ieee.org).
8. Д.А. Петров, “Алгоритмы формирования ортогональных хорошо локализованных базисов» // Математическое моделирование, 2010, №3, Том 22, С. 45-54.
9. А. Оппенгейм, Р. Шафер, “Цифровая обработка сигналов / Москва: Техносфера, 2006.
10. P.P. Vaidyanathan, «Multirate Systems and Filter Banks” / Englewood Clifs, NJ: Prentice-Hall, 1993.
11. G. Cariolaro, F.C. Vagliani, “An OFDM scheme with half complexity” // IEEE J. Select. Areas Commun., vol. 13, pp. 1586-1599, Dec. 1995.
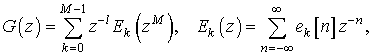 (3)
(3)