СОПОСТАВЛЕНИЕ ПЕЧАТНЫХ АНТЕНН КРУГОВОЙ ПОЛЯРИЗАЦИИ С РАЗНЫМИ СХЕМАМИ ПИТАНИЯ
С.
Е. Банков1, А. Г. Давыдов2, К. Б. Папилов1
1Институт
радиотехники и электронки им. В.А.Котельникова РАН
2МКБ «Компас»
Получена
2 марта 2010 г.
Аннотация. Рассмотрены три схемы питания
печатной антенны с круговой поляризацией: одноэлементная, двухэлементная с
реактивным делителем мощности и двухэлементная с балансным делителем мощности.
Схемы питания и антенны на их основе сравниваются по трем показателям качества:
полоса рабочих частот, минимальный коэффициент усиления антенны в полосе
частот, минимальный коэффициент эллиптичности в полосе частот. Сравнение антенн
осуществляется в пространстве показателей качества с использованием методов
векторной оптимизации. Установлена эквивалентность двух схем: одноэлементной и
двухэлементной с реактивным делителем мощности.
Ключевые слова: печатная антенна, схема питания, антенна
круговой поляризации.
1. Постановка задачи
Печатные антенны (ПА), излучающие и принимающие волны круговой поляризации находят широкое применение в различных радиоэлектронных системах [1]. К их числу можно отнести, например, системы спутниковой навигации [2].
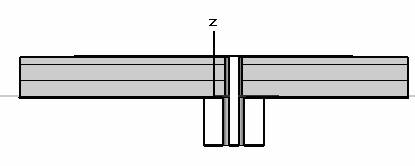
ПА представляет собой открытый полосковой резонатор, который связан с волнами излучения свободного пространства. Резонаторы могут иметь разную форму полоскового проводника: прямоугольную, круглую, квадратную и т.д. ПА могут отличаться также разными способами связи с внешней схемой. Наибольшее распространение получили ПА прямоугольной формы, которые имеют элемент возбуждения в виде металлического штыря (см. рис. 1 а,б). Металлический штырь соединяется с центральным проводником питающей ПА линии передачи. В качестве линии передачи может использоваться коаксиальная или микрополосковая линии. В последнем случае ПА и микрополосковая линия имеют общий экран.
а
б
Рис. 1
Собственные колебания полоскового резонатора обычно рассматриваются как колебания полуволнового отрезка линии передачи с нагрузками типа холостой ход на концах. В качестве линии передачи выступает плоский волновод (ПВ), который образуется в области между верхним полосковым проводником и нижним проводником – экраном. Обрыв полоскового проводника создает для основной Т – волны ПВ режим, близкий к холостому ходу. Отметим, что часть мощности при отражении от обрыва проводника излучается в свободное пространство. Этот эффект определяет конечное значение потерь на излучение из полоскового резонатора.
Волны ПВ могут распространяться как вдоль оси 0х (см. рис. 1), так и вдоль оси 0у. При этом они формируют два разных колебания. Основное их отличие состоит в том, что они излучают в свободное пространство волны, имеющие линейные ортогональные поляризации поля. Для создания излучения с круговой поляризацией в полосковом резонаторе необходимо одновременно возбудить два указанных колебания. При этом колебания должны быть равны по модулю и сдвинуты по фазе на девяносто градусов.
д
Рис. 2
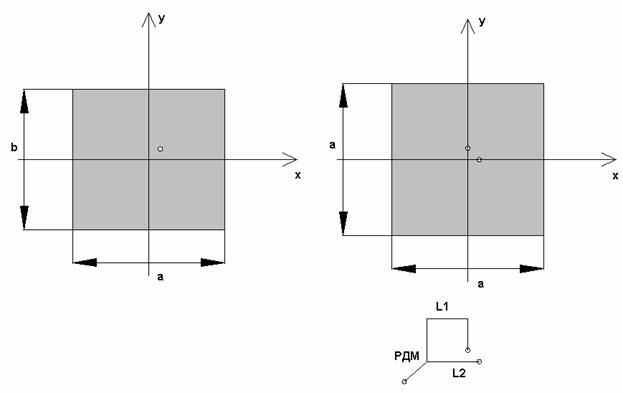
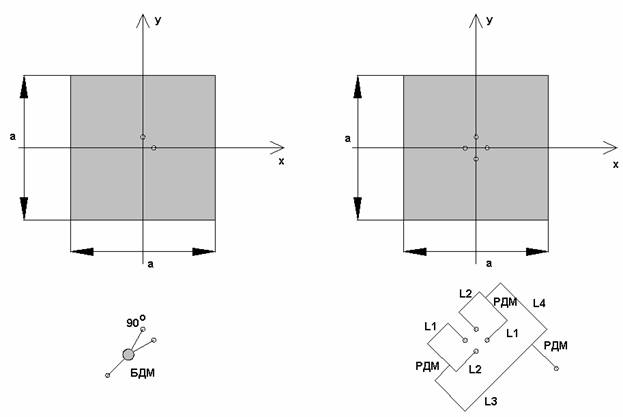
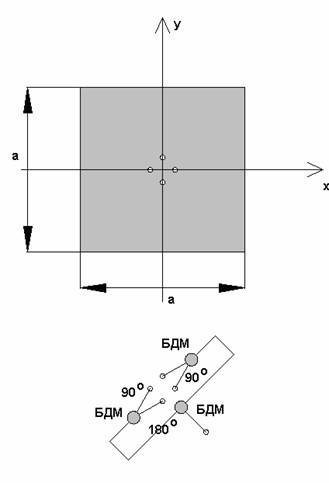
Задача возбуждения в ПА ортогональных колебаний с требуемыми амплитудно-фазовыми соотношениями решается путем использования специальных схем питания. Они показаны на рис. 2 а-д. Во всех вариантах, за исключением показанного на рис. 2 а, схема питания состоит из многоканального делителя мощности (МДМ) и элемента возбуждения. Количество элементов возбуждения может меняться от одного до четырех. В зависимости от этого схемы называют одноэлементными, двухэлементными и т.д.
Одноэлементная схема не
требует использования МДМ. Для нормального функционирования ПА она должна иметь
не квадратную, а прямоугольную форму так, чтобы резонансные частоты
ортогональных колебаний отличались друг от друга. Отметим, что приближенно
резонансная частота такого колебания ![]() определяется следующим условием:
определяется следующим условием:
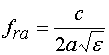 , (1)
, (1)
где ![]() - длина стороны ПА, вдоль которой
распространяется Т – волна, образующая данное колебание,
- длина стороны ПА, вдоль которой
распространяется Т – волна, образующая данное колебание, ![]() - относительная диэлектрическая
проницаемость подложки ПА,
- относительная диэлектрическая
проницаемость подложки ПА, ![]() - скорость света в вакууме. Индекс
- скорость света в вакууме. Индекс ![]() показывает, что
параметр
показывает, что
параметр ![]() относится
к колебанию, образованному Т – волной, движущейся вдоль стороны длиной
относится
к колебанию, образованному Т – волной, движущейся вдоль стороны длиной ![]() .
.
В других схемах возбуждения
ПА длины сторон ![]() и
и
![]() равны друг
другу и, следовательно, резонансные частоты ортогональных колебаний
равны друг
другу и, следовательно, резонансные частоты ортогональных колебаний ![]() и
и ![]() совпадают.
совпадают.
МДМ состоит из нескольких элементарных делителей мощности (ЭДМ), которые могут иметь элементы, обеспечивающие развязку боковых плеч – балансные сопротивления. ЭДМ, не имеющие таких резистивных элементов, получили название реактивных делителей мощности (РДМ), а делители с сопротивлениями называют балансными делителями мощности (БДМ). Они отличаются от РДМ согласованием всех входов и развязкой боковых плеч между собой.
Наряду с ЭДМ схема МДМ содержит ряд отрезков линий передачи, которые обеспечивают необходимые для работы ПА фазовые соотношения между амплитудами волн, поступающими на элементы возбуждения.
Целью данной работы является сопоставление ПА с разными схемами питания по совокупности показателей качества (ПК). Для этого мы воспользуемся методикой векторной оптимизации (ВО), изложенной в работе [3]. Эта методика формулирует объективный, математически строгий критерий сравнения разных технических объектов - безусловный критерий предпочтения (БКП), использование которого позволяет дать ответ на вопрос о том, какая из ПА изображенных на рис. 2, лучше других.
Важным этапом применения ВО является формулировка ПК. Под ПК понимается любая неотрицательная числовая характеристика устройства, которая монотонно уменьшается при улучшении его качества. Формулировка ПК является субъективным процессом, который связан с предпочтениями проектировщика. Поэтому результат ВО зависит от этих предпочтений, которые выражаются в конкретной совокупности ПК.
Будем описывать ПА с помощью
следующих ПК ![]() :
:
![]() ,
,
![]() ,
,
где ![]() - центральная частота рабочего диапазона
ПА,
- центральная частота рабочего диапазона
ПА, ![]() - полоса
рабочих частот ПА,
- полоса
рабочих частот ПА, ![]() -
коэффициент передачи по напряжению со входа ПА в волны излучения свободного
пространства рабочей поляризации,
-
коэффициент передачи по напряжению со входа ПА в волны излучения свободного
пространства рабочей поляризации, ![]() - коэффициент эллиптичности ПА.
- коэффициент эллиптичности ПА.
Из соотношений (2) видно,
что ПК ![]() имеет
смысл добротности ПА и характеризует ее диапазонные свойства. При этом ПА тем
лучше, чем меньше ее добротность. Такое определение ПК оправдано в том случае,
если в антенне потери на излучение существенно больше тепловых потерь. Данное
предположение ограничивает класс ПА, для которых будут справедливы результаты,
полученные ниже. Можно только отметить, что наиболее интересные с практической
точки зрения ПА, имеющие высокий коэффициент полезного действия, удовлетворяют
сформулированному выше ограничению.
имеет
смысл добротности ПА и характеризует ее диапазонные свойства. При этом ПА тем
лучше, чем меньше ее добротность. Такое определение ПК оправдано в том случае,
если в антенне потери на излучение существенно больше тепловых потерь. Данное
предположение ограничивает класс ПА, для которых будут справедливы результаты,
полученные ниже. Можно только отметить, что наиболее интересные с практической
точки зрения ПА, имеющие высокий коэффициент полезного действия, удовлетворяют
сформулированному выше ограничению.
Коэффициент передачи ![]() будет определен ниже.
Он показывает суммарные потери мощности, которые обусловлены отражениями от
входа ПА и возбуждением волн нерабочей поляризации. В соответствии с формулами
(2) мы выражает его в децибелах и берем максимальное, то есть наихудшее
значение в рабочем диапазоне частот.
будет определен ниже.
Он показывает суммарные потери мощности, которые обусловлены отражениями от
входа ПА и возбуждением волн нерабочей поляризации. В соответствии с формулами
(2) мы выражает его в децибелах и берем максимальное, то есть наихудшее
значение в рабочем диапазоне частот.
Под коэффициентом
эллиптичности понимается соответствующий стандартный параметр антенны круговой
поляризации, равный отношению осей эллипса поляризации. Для волны с идеальной
круговой поляризацией ![]() равен
единице (выраженный в децибелах нулю). В качестве ПК мы берем максимальное
значение
равен
единице (выраженный в децибелах нулю). В качестве ПК мы берем максимальное
значение ![]() в
полосе частот.
в
полосе частот.
2. Элементы теории ВО
Рассмотрим существенные для нашего анализа элементы теории ВО. В соответствии с работой [3] ВО разных устройств проводится в два этапа. На первом этапе оптимизируется каждое из них в отдельности, а на втором этапе сравниваются между собой оптимизированные устройства.
Отметим, что, говоря о ПА,
мы имеем в виду множество антенн с одинаковой структурой, показанной на
рис. 2
и разными значениями параметров ![]() . Каждая ПА характеризуется своей
совокупностью (вектором)
. Каждая ПА характеризуется своей
совокупностью (вектором) ![]() параметров. Их изменение в пределах
заданной области допустимых значений порождает множество ПА, которое называют
множеством строго допустимых решений (МСД). Каждый элемент этого множества
характеризуется своей совокупностью (вектором) показателей качества
параметров. Их изменение в пределах
заданной области допустимых значений порождает множество ПА, которое называют
множеством строго допустимых решений (МСД). Каждый элемент этого множества
характеризуется своей совокупностью (вектором) показателей качества ![]() , которая является
функцией вектора
, которая является
функцией вектора ![]() :
:
![]() . Из-за
указанной функциональной зависимости возникает упомянутое МСД.
. Из-за
указанной функциональной зависимости возникает упомянутое МСД.
Целью ВО применительно к каждой ПА является выделение из МСД другого множества, являющегося частью МСД, так называемого множества нехудщих решений (МНХ). Нехудшие решения являются оптимальными по отношению к другим элементам МСД, не вошедшим в МНХ. Таким образом, результат ВО – это не одно, а множество оптимальных (нехудших) решений. В этом принципиальное отличие ВО от более привычной скалярной оптимизации, в рамках которой устройства сравниваются по одному ПК, который часто называют целевой функцией. Скалярная оптимизация дает единственное оптимальное решение. В тоже время скалярная постановка задачи предполагает существенно большую степень субъективности получаемого единственного решения, которое полностью зависит от способа формулировки целевой функции. При этом необходимо с помощью одной функции отразить совокупность разных и обычно противоречивых технических требований к устройству. По этой причине векторный подход к оптимизации представляется более объективным, чем скалярный.
Сравнение устройств,
принадлежащих к МСД, осуществляется с помощью уже упоминавшегося БКП.
Сформулируем его в явном виде. Пусть мы имеем две ПА, которые назовем ПА1 и
ПА2, характеризуемые векторами ![]() . Тогда БКП утверждает следующее:
. Тогда БКП утверждает следующее:
ПА1 лучше ПА2, если, по крайней мере, один ПК у нее меньше аналогичного ПК ПА2, а другие ПК ПА1 меньше или равны аналогичным ПК ПА2;
ПА1 хуже ПА2, если, по крайней мере, один ПК у нее больше аналогичного ПК ПА2, а другие ПК ПА1 больше или равны аналогичным ПК ПА2;
ПА1 и ПА2 эквивалентны,
если ![]() ;
;
ПА1 и ПА2 несравнимы, если одна часть ПК ПА1 больше аналогичных ПК ПА2, а другая часть ПК ПА1 меньше аналогичных ПК ПА2.
Применение БКП разделяет элементы МСД на две части, одна из которых составляет МНХ. Отличительной чертой МНХ является то, что все устройства (решения), входящие в него, несравнимы друг с другом. Важно также, что для любого решения, не вошедшего в МНХ всегда можно найти из МНХ безусловно лучшее решение. Нетрудно убедиться, что геометрически МНХ представляет собой левую нижнюю границу МСД.
Таким образом, на первом этапе ВО мы будем искать МНХ для каждой из ПА. На втором этапе ВО мы будем сравнивать МНХ для разных ПА друг с другом.
3. Математическая модель ПА
Построение корректной математической модели ПА с круговой поляризацией является громоздкой задачей, так как оно связано с анализом электромагнитного поля в области со сложной геометрией. Подобный анализ возможен с использованием современных программных средств, таких как HFSS [4], Microwave Studio, FEKO [5]. Однако их применение, требующее большого количества времени, входит в определенное противоречие с процедурой ВО, особенностью которой является необходимость анализа весьма большого числа вариантов.
Поэтому мы остановились
на более простой резонаторной модели ПА [6], которая, с одной стороны, не
требует больших затрат компьютерных ресурсов, а, с другой стороны, качественно
верно описывает поведение ПК антенны в зависимости от изменения ее параметров.
В рамках резонаторной модели ПА моделируется закрытым резонатором, имеющим
форму параллелепипеда (см. рис. 3), расположенного на бесконечном идеально
проводящем экране. На его горизонтальных гранях при ![]() установлены граничные условия на
идеально проводящей поверхности, а на вертикальных граничные условия на
магнитной стенке.
установлены граничные условия на
идеально проводящей поверхности, а на вертикальных граничные условия на
магнитной стенке.
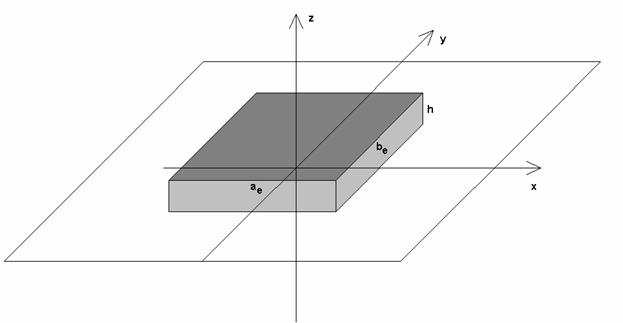
Рис. 3
Размеры резонатора ![]() в плоскости XOY: отличаются от размеров ПА. Это
отличие учитывает краевые эффекты, возникающие вблизи обрыва полоскового
проводника.
в плоскости XOY: отличаются от размеров ПА. Это
отличие учитывает краевые эффекты, возникающие вблизи обрыва полоскового
проводника.
Учет краевых эффектов может быть осуществлен известным способом, например, в соответствии с методикой изложенной в работе [6]. Резонатор с электрическими и магнитными стенками не излучает в свободное пространство. Для учета излучения на боковых поверхностях вводятся магнитные токи, которые находятся с помощью тангенциальных компонент электрического поля колебаний закрытой структуры. Эти токи создают поле, уносящее конечную часть энергии в бесконечность. Определяя ее, можно найти величину добротности излучения собственного колебания резонатора.
Возбуждения резонатора осуществляется штыревыми элементами возбуждения, в которые включены сосредоточенные источники напряжения, моделирующие выходы схемы питания ПА.
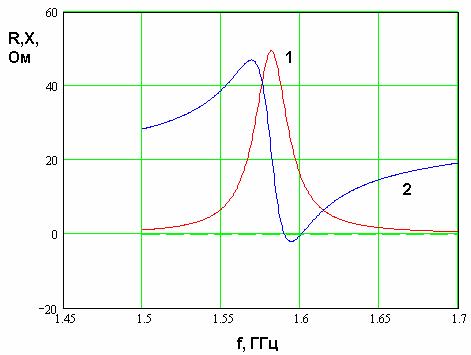
Рис. 4
Говоря о модели ПА,
необходимо отметить одну важную особенность ее работы, а именно наличие так
называемой остаточной индуктивности. Для пояснения этого эффекта рассмотрим
типичные частотные зависимости действительной ![]() и мнимой
и мнимой ![]() частей входного сопротивления от частоты,
показанные на рис. 4. На резонансной частоте
частей входного сопротивления от частоты,
показанные на рис. 4. На резонансной частоте ![]() действительная часть импеданса (кривая 1)
достигает своего максимума, а мнимая (кривая 2) имеет точку перегиба. При этом
мнимая часть на частоте
действительная часть импеданса (кривая 1)
достигает своего максимума, а мнимая (кривая 2) имеет точку перегиба. При этом
мнимая часть на частоте ![]() не равна нулю. Обычно
не равна нулю. Обычно ![]() , что можно интерпретировать как
наличие в эквивалентной схеме антенны последовательной индуктивности, которую будем
называть остаточной. Ее появление связано с конкретным способом возбуждения, а
именно с помощью металлического штыря.
, что можно интерпретировать как
наличие в эквивалентной схеме антенны последовательной индуктивности, которую будем
называть остаточной. Ее появление связано с конкретным способом возбуждения, а
именно с помощью металлического штыря.
Остаточная индуктивность
может иметь весьма большое сопротивление, наличие которого препятствует
эффективному согласованию ПА. Для компенсации его влияния в схему возбуждения
ПА вводят емкость ![]() ,
которую выбирают из следующего условия:
,
которую выбирают из следующего условия:
Выполнение соотношения (3) обеспечивает на резонансной частоте действительное значение входного сопротивления ПА. Таким образом, резонаторная модель ПА должна обеспечивать возможность включения компенсирующей емкости.
Описанная выше модель ПА
позволяет находить ее ПК (2), при этом требуется вычисление коэффициента
эллиптичности антенны и коэффициента передачи ![]() . Коэффициент эллиптичности рассчитывается
в направлении максимума диаграммы направленности, то есть вдоль оси 0z. Реальная ПА может излучать волны с
неидеальной круговой поляризацией. Для определенности считаем, что рабочей
является правая круговая поляризация. В этом случае часть мощности будет
уходить в левую круговую поляризацию. Пусть
. Коэффициент эллиптичности рассчитывается
в направлении максимума диаграммы направленности, то есть вдоль оси 0z. Реальная ПА может излучать волны с
неидеальной круговой поляризацией. Для определенности считаем, что рабочей
является правая круговая поляризация. В этом случае часть мощности будет
уходить в левую круговую поляризацию. Пусть ![]() и
и ![]() - z-ые компоненты вектора Пойнтинга волн левой и правой
круговой поляризации, определенные в дальней зоне ПА на оси 0z. Тогда под коэффициентом передачи в
волну рабочей поляризации будем понимать следующее отношение:
- z-ые компоненты вектора Пойнтинга волн левой и правой
круговой поляризации, определенные в дальней зоне ПА на оси 0z. Тогда под коэффициентом передачи в
волну рабочей поляризации будем понимать следующее отношение:
Этот коэффициент показывает, какая часть полной энергии излучения соответствует волне требуемой поляризации.
Для определения
коэффициента передачи ![]() ,
который описывает все потери мощности, необходимо учесть ослабление сигнала, обусловленное
рассогласованием ПА по входу:
,
который описывает все потери мощности, необходимо учесть ослабление сигнала, обусловленное
рассогласованием ПА по входу:
где ![]() - коэффициент отражения от ПА.
- коэффициент отражения от ПА.
Представленная выше резонаторная модель ПА хорошо известна в литературе, что избавляет от необходимости ее подробного описания. С ее помощью можно рассчитывать все интересующие нас параметры ПА, в том числе и параметры ПА с многоэлементными схемами питания.
4. Сопоставление ПА с двух- и четырехэлементными схемами питания
На данном этапе выясним целесообразность использования четырехэлементных схем питания. Принцип их функционирования не отличается от принципа функционирования двухэлементной схемы, в которой каждый из выходов схемы питания должен возбуждать одно из двух ортогональных колебаний. При этом амплитуды колебаний должны быть равными по модулю и сдвинутыми по фазе на 90 градусов.
Если бы штырь, введенный
в резонатор, возбуждал только поле рабочих колебаний, то данная задача
полностью решалась с помощью двухэлементной схемы, так как колебание ![]() имеет нулевое
электрическое поле в плоскости
имеет нулевое
электрическое поле в плоскости ![]() и не возбуждается расположенным в этой
плоскости элементом и, наоборот, колебание
и не возбуждается расположенным в этой
плоскости элементом и, наоборот, колебание ![]() не возбуждается элементом расположенным в
плоскости
не возбуждается элементом расположенным в
плоскости ![]() (см.
рис. 2 б). Будем понимать под колебаниями
(см.
рис. 2 б). Будем понимать под колебаниями ![]() ,
,![]() колебания, образованные движением Т – волн
ПВ вдоль боковых граней ПА, имеющих длину соответственно
колебания, образованные движением Т – волн
ПВ вдоль боковых граней ПА, имеющих длину соответственно ![]() и
и ![]() .
.
Штыревой элемент
возбуждения, однако, взаимодействует не только с полями рабочих колебаний, но и
порождает в ПА сложное реактивное поле, которое не имеет нулей в плоскостях ![]() или
или ![]() . По этой причине при подаче
сигнала, например, на вход в плоскости
. По этой причине при подаче
сигнала, например, на вход в плоскости ![]() электрические токи возникают не только на
штыре, расположенном в этой плоскости, но и на штыре, который находится в
плоскости
электрические токи возникают не только на
штыре, расположенном в этой плоскости, но и на штыре, который находится в
плоскости ![]() .
Эти токи возбуждают колебание
.
Эти токи возбуждают колебание ![]() , которое в идеальном случае не должно
возбуждаться. Таким образом, возникает нежелательная связь рабочих колебаний,
которая приводит, в первую очередь, к снижению коэффициента эллиптичности ПА.
, которое в идеальном случае не должно
возбуждаться. Таким образом, возникает нежелательная связь рабочих колебаний,
которая приводит, в первую очередь, к снижению коэффициента эллиптичности ПА.
Использование
четырехэлементной схемы позволяет исключить данный эффект за счет симметрии
относительно координатных плоскостей, которую имеет в данном случае ПА (см.
рис. 2 г,д). При идеальной работе схемы
питания штыри, расположенные в плоскостях ![]() и
и ![]() , возбуждаются в противофазе. За счет этого
ближнее поле также как и поле рабочих колебаний имеет нули в требуемых
плоскостях, что обеспечивает развязку элементов возбуждения. Развязка элементов
возбуждения устраняет, в свою очередь связь между ортогональными колебаниями
ПА.
, возбуждаются в противофазе. За счет этого
ближнее поле также как и поле рабочих колебаний имеет нули в требуемых
плоскостях, что обеспечивает развязку элементов возбуждения. Развязка элементов
возбуждения устраняет, в свою очередь связь между ортогональными колебаниями
ПА.
Сравним далее коэффициент эллиптичности ПА с идеальными двух- и четырехэлементными схемами питания. Под идеальной схемой мы понимает схему, которая на любой частоте формирует требуемое амплитудно – фазовое распределение на своих выходах. При такой постановке задачи коэффициент эллиптичности четырехэлементной ПА равен единице, а выраженный в децибелах нулю. Поэтому задача сводится к анализу коэффициента эллиптичности ПА с двухэлементной схемой питания.
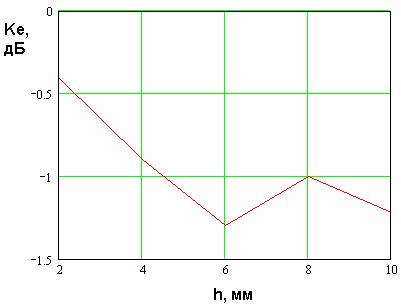
Рис. 5
На рис. 5 показана зависимость
коэффициента эллиптичности ![]() ПА с двумя элементами возбуждения от
высоты ПА. Антенна имеет следующие параметры:
ПА с двумя элементами возбуждения от
высоты ПА. Антенна имеет следующие параметры: ![]() ,
, ![]() мм, тангенс угла потерь
мм, тангенс угла потерь ![]() в диэлектрике равен
0.001, в качестве материала, из которого выполнены металлические части
конструкции ПА взята медь, радиус штырей
в диэлектрике равен
0.001, в качестве материала, из которого выполнены металлические части
конструкции ПА взята медь, радиус штырей ![]() мм, элементы возбуждения смещены
относительно центра ПА на расстояние 2.2 мм.
мм, элементы возбуждения смещены
относительно центра ПА на расстояние 2.2 мм.
При указанных выше
параметрах ПА имеет центральную частоту рабочего диапазона ![]() равную 1.6 ГГц. Из рис. 5 видно,
что при увеличении высоты ПА ее коэффициент эллиптичности падает, причем весьма
существенно. Причина этого состоит в уменьшении добротности рабочих колебаний
равную 1.6 ГГц. Из рис. 5 видно,
что при увеличении высоты ПА ее коэффициент эллиптичности падает, причем весьма
существенно. Причина этого состоит в уменьшении добротности рабочих колебаний ![]() , зависимость которой от
высоты
, зависимость которой от
высоты ![]() показана
на рис. 6.
показана
на рис. 6.
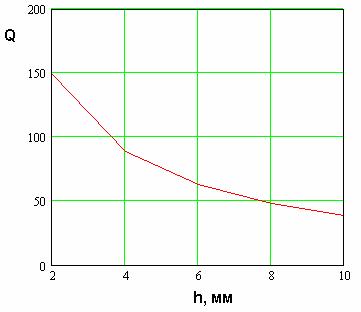
Рис. 6
Из общих принципов работы
объемных резонаторов следует, что чем выше добротность резонатора, тем более
интенсивно возбуждается на резонансной частоте его колебание. Поэтому при
больших значениях ![]() поле
рабочего колебания много больше реактивного поля и, следовательно, эффект связи
ортогональных колебаний, который обусловлен присутствием реактивного поля,
проявляется относительно слабо. При уменьшении добротности его влияние
возрастает.
поле
рабочего колебания много больше реактивного поля и, следовательно, эффект связи
ортогональных колебаний, который обусловлен присутствием реактивного поля,
проявляется относительно слабо. При уменьшении добротности его влияние
возрастает.
Коэффициент эллиптичности
ПА с двумя элементами возбуждения может улучшить использование третьего
металлического штыря, расположенного в центре ПА. С его помощью удается
уменьшить амплитуду реактивного поля и приблизить его структуру к оптимальной,
то есть имеющей нули в требуемых областях внутри ПА. На рис. 7 показана
частотная зависимость ![]() такой
антенны. Кривая 1 получена для ПА с двумя элементами возбуждения и
металлическим штырем. Для сравнения на рис. 7 показана кривая 2,
соответствующая четырехэлементному возбуждению ПА. Видно, что в данном случае
коэффициент эллиптичности незначительно отличается от своего оптимального
значения.
такой
антенны. Кривая 1 получена для ПА с двумя элементами возбуждения и
металлическим штырем. Для сравнения на рис. 7 показана кривая 2,
соответствующая четырехэлементному возбуждению ПА. Видно, что в данном случае
коэффициент эллиптичности незначительно отличается от своего оптимального
значения.
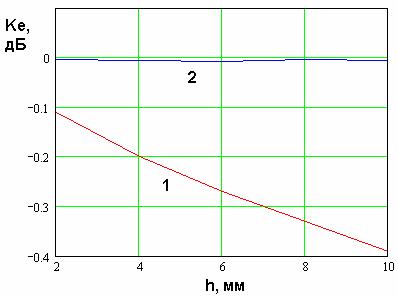
Рис. 7
Таким образом, можно сделать следующие выводы. Четырехэлементная схема питания имеет существенное преимущество по сравнению с двухэлементной, но дает незначительный выигрыш по сравнению с двухэлементной схемой дополненной пассивным штырем в центре ПА. В тоже время двухэлементная схема имеет меньшие размеры, чем четырехэлементная и, следовательно, меньшие потери мощности. Поэтому при условии практического равенства коэффициентов эллиптичности предпочтение следует отдать двухэлементной схеме.
5. Оптимизация одноэлементной схемы по совокупности ПК
Определим совокупность
свободных параметров одноэлементной схемы, которые будут варьироваться в ходе
ВО. Полный набор исходных параметров имеет следующий вид: ![]() - высота ПА,
- высота ПА, ![]() - размеры ПА в горизонтальной плоскости,
- размеры ПА в горизонтальной плоскости,
![]() -
диэлектрическая проницаемость подложки ПА,
-
диэлектрическая проницаемость подложки ПА, ![]() - смещения точки возбуждения относительно
центра ПА,
- смещения точки возбуждения относительно
центра ПА, ![]() -
радиус штыревого элемента возбуждения,
-
радиус штыревого элемента возбуждения, ![]() - компенсирующая емкость.
- компенсирующая емкость.
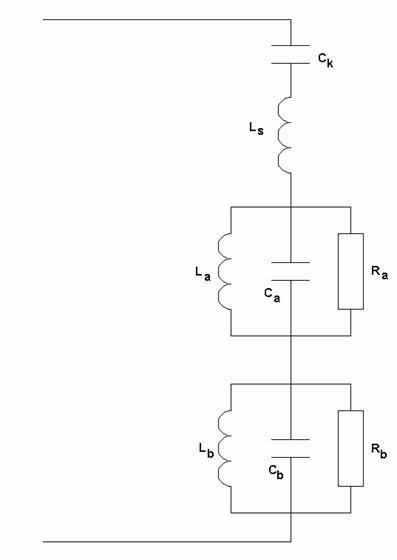
Рис. 8
Для удобства описания ПА
целесообразно ввести ее эквивалентную схему, которая описывает поведение ПА
вблизи резонансных частот ортогональных колебаний. Она показана на рис. 8. Один
контур описывает колебание ![]() , а другой колебание
, а другой колебание ![]() , индуктивность
, индуктивность ![]() - остаточная
индуктивность штыря, а емкость
- остаточная
индуктивность штыря, а емкость ![]() - компенсирующая емкость. Мы рассматриваем
ПА при условии
- компенсирующая емкость. Мы рассматриваем
ПА при условии ![]() ,
то есть почти квадратную, у которой
,
то есть почти квадратную, у которой ![]() . В этом случае параметры контуров близки
друг другу. Тем не менее численные расчеты показывают, что некоторое отличие
между ними существует. Оно обусловлено, в первую очередь, отличием добротностей
колебаний
. В этом случае параметры контуров близки
друг другу. Тем не менее численные расчеты показывают, что некоторое отличие
между ними существует. Оно обусловлено, в первую очередь, отличием добротностей
колебаний ![]() и
и ![]() . Между ними было
получено приближенное соотношение:
. Между ними было
получено приближенное соотношение:
Из-за отличия добротностей
для получения одинаковых значений резонансных сопротивлений контуров ![]() и
и ![]() сдвиги
сдвиги ![]() и
и ![]() точки включения элемента возбуждения по
осям 0х и 0у должны быть связаны следующим соотношением:
точки включения элемента возбуждения по
осям 0х и 0у должны быть связаны следующим соотношением:
Значение компенсирующей
емкости выбирается из условия аналогичного условию (3), в котором в качестве ![]() надо взять среднюю
между
надо взять среднюю
между ![]() и
и
![]() частоту:
частоту:
С учетом соотношений (6)
– (8) можно ввести следующие обобщенные параметры, которые являются функциями
исходных параметров: ![]() ,
,![]() - резонансные частоты
ортогональных колебаний,
- резонансные частоты
ортогональных колебаний, ![]() - их добротность,
- их добротность, ![]() - активная часть входного
сопротивления. Под добротностью
- активная часть входного
сопротивления. Под добротностью ![]() можно понимать добротность любого из
ортогональных колебаний, так как они связаны формулой (6). Для определенности
пусть это будет
можно понимать добротность любого из
ортогональных колебаний, так как они связаны формулой (6). Для определенности
пусть это будет ![]() .
Пусть также
.
Пусть также ![]() .
.
При выполнении ВО мы
полагали следующие обобщенные параметры свободными: ![]() ,
, 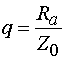 ,
, ![]() - характеристическое сопротивление линии, подключенной к ПА,
которое равнялось фиксированной величине 50 Ом. Обобщенные параметры
- характеристическое сопротивление линии, подключенной к ПА,
которое равнялось фиксированной величине 50 Ом. Обобщенные параметры ![]() и
и ![]() фиксировались. Компенсирующая
емкость выбиралась из условия (3). Кроме того, сдвиги точки возбуждения по
разным осям координат выбирались с учетом условия (7). Диэлектрическая проницаемость
ПА и радиус элемента возбуждения принимались равными 10 и 0.5 мм соответственно. Таким образом, все исходные параметры
однозначно определялись по значениям свободных и фиксированных обобщенных
параметров с учетом условий (3) и (7). Это позволяет в дальнейшем оперировать
только обобщенными параметрами, что удобнее, чем использование исходных
параметров.
фиксировались. Компенсирующая
емкость выбиралась из условия (3). Кроме того, сдвиги точки возбуждения по
разным осям координат выбирались с учетом условия (7). Диэлектрическая проницаемость
ПА и радиус элемента возбуждения принимались равными 10 и 0.5 мм соответственно. Таким образом, все исходные параметры
однозначно определялись по значениям свободных и фиксированных обобщенных
параметров с учетом условий (3) и (7). Это позволяет в дальнейшем оперировать
только обобщенными параметрами, что удобнее, чем использование исходных
параметров.
Рассмотрим результаты ВО,
полученные для следующих конкретных значений параметров: ![]() =1.6 ГГц,
=1.6 ГГц, ![]() =40. Пределы изменения свободных
параметров были следующими:0<
=40. Пределы изменения свободных
параметров были следующими:0<![]() <0.1 ГГц, 0.1<
<0.1 ГГц, 0.1<![]() <2. Полоса рабочих частот ПА менялась
в пределах от 0.01 до 0.2 ГГц. Множество свободных параметров и ПК
<2. Полоса рабочих частот ПА менялась
в пределах от 0.01 до 0.2 ГГц. Множество свободных параметров и ПК ![]() подвергались дискретизации,
при этом по каждой переменной было выбрано по 20 точек с одинаковым шагом.
Таким образом, общее число вариантов, вошедших в МСД, равнялось 8000. Следующий
этап ВО – применение БКП и определение МНХ.
подвергались дискретизации,
при этом по каждой переменной было выбрано по 20 точек с одинаковым шагом.
Таким образом, общее число вариантов, вошедших в МСД, равнялось 8000. Следующий
этап ВО – применение БКП и определение МНХ.
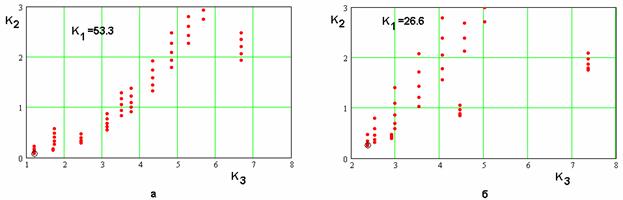
Рис. 9
Интересные результаты
позволяет получить анализ сечений МСД, соответствующих фиксированным значениям ![]() . На рис. 9 а,б показаны
два таких сечения в пространстве ПК
. На рис. 9 а,б показаны
два таких сечения в пространстве ПК ![]() . Видно, что каждое сечение содержит одно
безусловно лучшее по БКП решение. Оно показано кружком. Наличие такого
безусловно лучшего решения позволяет без использования процедуры поиска МНХ
отбросить из рассмотрения все худшие варианты и анализировать только множество,
состоящее из безусловно лучших для каждого фиксированного
. Видно, что каждое сечение содержит одно
безусловно лучшее по БКП решение. Оно показано кружком. Наличие такого
безусловно лучшего решения позволяет без использования процедуры поиска МНХ
отбросить из рассмотрения все худшие варианты и анализировать только множество,
состоящее из безусловно лучших для каждого фиксированного ![]() вариантов. Все элементы такого
множества несравнимы друг с другом и, следовательно, они составляют МНХ. В
пространстве трех ПК это множество является кривой, которая показана на рис.
10.
вариантов. Все элементы такого
множества несравнимы друг с другом и, следовательно, они составляют МНХ. В
пространстве трех ПК это множество является кривой, которая показана на рис.
10.
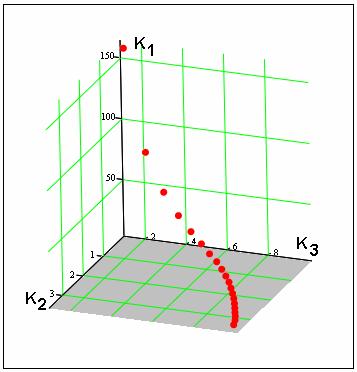
Рис. 10
Важным результатом ВО
является не только усечение МСД и формирование МНХ, но и формирование множества
параметров, которые соответствуют нехудшим решениям. Эти множества показаны на
рис. 11 а,б. На рис. 11 а представлена зависимость параметра ![]() от ПК
от ПК ![]() МНХ, а на рис. 11 б
параметра
МНХ, а на рис. 11 б
параметра ![]() .
Обращает на себя внимание изрезанный характер кривых 1, соответствующих прямому
расчету параметров. Кривые 2 получены в результате расчета по аппроксимационным
формулам, о которых будет сказано ниже. Изрезанность кривых 1 на рис. 11 а,б
связана с дискретизацией МСД, что подтверждается зависимостью
.
Обращает на себя внимание изрезанный характер кривых 1, соответствующих прямому
расчету параметров. Кривые 2 получены в результате расчета по аппроксимационным
формулам, о которых будет сказано ниже. Изрезанность кривых 1 на рис. 11 а,б
связана с дискретизацией МСД, что подтверждается зависимостью ![]() от
от ![]() , показанной на рис. 12. Она
отличается от кривой 1 на рис. 11 а только тем, что она получена в результате
дискретизации параметров на тех же интервалах, что и раньше, но с
использованием 40 точек. Видно, что указанная зависимость стала существенно
более гладкой. Необходимо отметить, что увеличение МСД, которое в новом
варианте содержит 64000 решений, резко увеличивает время, необходимое для
получения МНХ. Поэтому лучшим способом избавиться от нестабильности,
обусловленной дискретизацией является аппроксимация зависимостей параметров от
ПК.
, показанной на рис. 12. Она
отличается от кривой 1 на рис. 11 а только тем, что она получена в результате
дискретизации параметров на тех же интервалах, что и раньше, но с
использованием 40 точек. Видно, что указанная зависимость стала существенно
более гладкой. Необходимо отметить, что увеличение МСД, которое в новом
варианте содержит 64000 решений, резко увеличивает время, необходимое для
получения МНХ. Поэтому лучшим способом избавиться от нестабильности,
обусловленной дискретизацией является аппроксимация зависимостей параметров от
ПК.
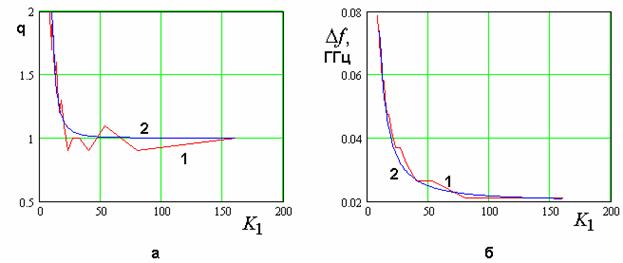
Рис. 11
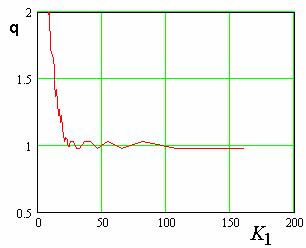
Рис. 12
Можно предложить
следующие аппроксимации зависимостей параметров ![]() и
и ![]() от
от ![]() :
:
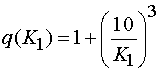 , (9)
, (9)
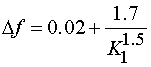 .
.
В формуле (9) ![]() определяется в
гигагерцах.
определяется в
гигагерцах.
Кривые 2 на рис. 11 а,б
получены по формулам (9). Далее с помощью этих формул было вновь найдено МНХ. Это
МНХ должно отличаться от исходного, так как ему соответствуют другие значения
параметров. Однако это отличие практически незаметно, что видно из рис. 13 на
котором представлены зависимости нехудших значений ПК ![]() от ПК
от ПК ![]() . Точки (1,2) соответствуют
исходному дискретному МНХ, а кривые 3,4 новому непрерывному МНХ, полученному с
помощью соотношений (9). Видно, что исходное и новое МНХ очень хорошо совпадают,
несмотря на то, что значения параметров
. Точки (1,2) соответствуют
исходному дискретному МНХ, а кривые 3,4 новому непрерывному МНХ, полученному с
помощью соотношений (9). Видно, что исходное и новое МНХ очень хорошо совпадают,
несмотря на то, что значения параметров ![]() и
и ![]() исходных и полученных по формулам (9)
могут заметно отличаться. Отсюда можно сделать вывод, что МНХ устойчиво по
отношению к вариациям параметров.
исходных и полученных по формулам (9)
могут заметно отличаться. Отсюда можно сделать вывод, что МНХ устойчиво по
отношению к вариациям параметров.
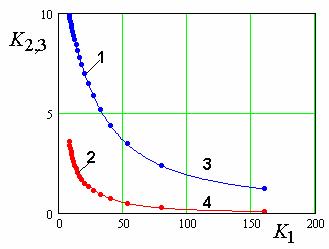
Рис. 13
6. Оптимизация по совокупности ПК двухэлементной схемы с РДМ
Функционирование ПА с двухэлементными схемами питания с РДМ хорошо описывается эквивалентной схемой, показанной на рис. 14. Эта эквивалентная схема необходима нам только в качестве иллюстрации для выбора обобщенных параметров структуры.
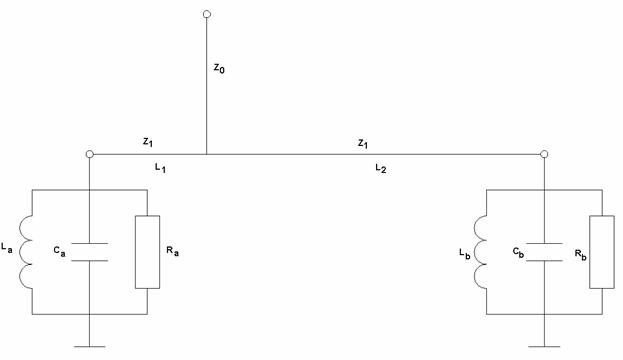
Рис. 14
Параметры контуров в
эквивалентной схеме одинаковы, так как ПА имеет квадратную форму, а элементы
питания сдвинуты от ее центра на одинаковое расстояние. Контуры подключены к
выходам РДМ, который представляет собой параллельное соединение линий передачи
разной длины ![]() и
и
![]() . Разница
между длинами
. Разница
между длинами ![]() выбирается
равной
выбирается
равной ![]() на
центральной частоте рабочего диапазона
на
центральной частоте рабочего диапазона ![]() , которая совпадает с резонансными
частотами
, которая совпадает с резонансными
частотами ![]() колебаний
ПА. Такой выбор длин линий передачи должен обеспечивать сдвиг фаз указанных
колебаний в 90 градусов.
колебаний
ПА. Такой выбор длин линий передачи должен обеспечивать сдвиг фаз указанных
колебаний в 90 градусов.
В качестве свободных
обобщенных параметров были выбраны ![]() и
и ![]() , которые связывают характеристическое
сопротивление боковых плеч РДМ -
, которые связывают характеристическое
сопротивление боковых плеч РДМ - ![]() с характеристическим сопротивлением
входной линии
с характеристическим сопротивлением
входной линии ![]() ,
а также сопротивление контура на резонансной частоте
,
а также сопротивление контура на резонансной частоте ![]() . Отметим, что классической
настройке схемы питания с РДМ соответствует случай
. Отметим, что классической
настройке схемы питания с РДМ соответствует случай ![]() . Ниже будет показано, что такая
настройка не всегда является наилучшей.
. Ниже будет показано, что такая
настройка не всегда является наилучшей.
По аналогии с предыдущим
случаем мы фиксировали параметры ![]() и
и ![]() , полагая их равными соответственно 10 и 0.5 мм. Кроме того, мы фиксировали значение добротности ПА, считая
ее равной 40 и центральную частоту рабочего диапазона
, полагая их равными соответственно 10 и 0.5 мм. Кроме того, мы фиксировали значение добротности ПА, считая
ее равной 40 и центральную частоту рабочего диапазона ![]() ГГц.
ГГц.
Отметим, что МСД и МНХ для антенны с РДМ оказались качественно и, что особенно интересно, количественно весьма близкими к МСД и МНХ ПА с одноэлементной схемой питания. Поэтому столь же детально, как в предыдущем случае мы их описывать не будем. Укажем на то, что МНХ представляет собой кривую в пространстве ПК. Она показана на рис. 15.
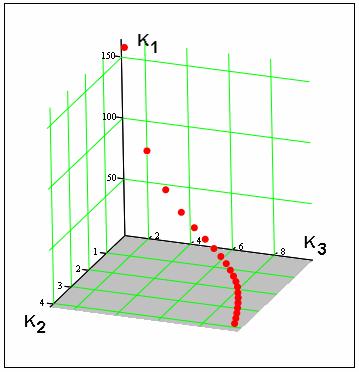
Рис. 15
7. Оптимизация по совокупности ПК двухэлементной схемы с БДМ
Данная задача более
простой по сравнению с рассмотренными выше. Простота ее обусловлена особенностями
БДМ, который имеет развязанные боковые плечи и обеспечивает сдвиг фаз между
сигналами в этих плечах, равный в точности 90 градусам. Поэтому в силу
идеальной развязки контуров, которые моделируют колебания ПА, они возбуждаются
независимо друг от друга с требуемыми соотношениями амплитуд и фаз. По этой
причине коэффициент эллиптичности такой ПА всегда равен своему предельному
значению, то есть единице, а ПК ![]() - нулю. Отсюда можно сразу сделать вывод о
том, что МНХ данной ПА представляет собой кривую, лежащую в плоскости
- нулю. Отсюда можно сразу сделать вывод о
том, что МНХ данной ПА представляет собой кривую, лежащую в плоскости ![]() =0. Параметры кривой
определяются частотной характеристикой ПА, то есть резонансной кривой. Можно
сразу сказать, что наилучшие значения ПК дают параметры, обеспечивающие
согласование антенны с питающей линией передачи.
=0. Параметры кривой
определяются частотной характеристикой ПА, то есть резонансной кривой. Можно
сразу сказать, что наилучшие значения ПК дают параметры, обеспечивающие
согласование антенны с питающей линией передачи.
Как и раньше, значения
параметров ![]() и
и ![]() , а также обобщенных
параметров
, а также обобщенных
параметров ![]() фиксировались.
Величины активного сопротивления ПА и компенсирующей емкости подбирались из
условия (3) и равенства
фиксировались.
Величины активного сопротивления ПА и компенсирующей емкости подбирались из
условия (3) и равенства ![]() . Результат ВО показан на рис. 16, на
котором представлено МНХ для данного типа ПА.
. Результат ВО показан на рис. 16, на
котором представлено МНХ для данного типа ПА.
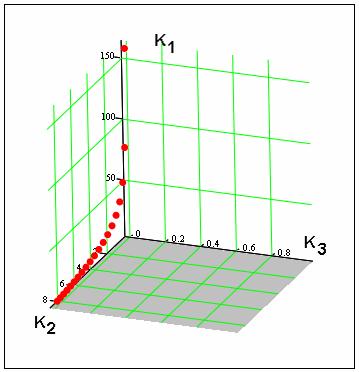
Рис. 16
8. Сопоставление ПА с разными схемами питания
Сопоставление ПА с
разными схемами питания удобно проводить графически. С этой целью на рис. 17
показаны проекции МНХ в пространстве ПК на плоскости ![]() и
и ![]() . Точки 1,2 представляют собой проекции МНХ
ПА с одноэлементой схемой питания и двухэлементой схемой с РДМ на плоскость
. Точки 1,2 представляют собой проекции МНХ
ПА с одноэлементой схемой питания и двухэлементой схемой с РДМ на плоскость ![]() , а точки 3,4 проекции
МНХ тех же ПА, но на плоскость
, а точки 3,4 проекции
МНХ тех же ПА, но на плоскость ![]() . Точки 4 соответствуют проекции на
плоскость
. Точки 4 соответствуют проекции на
плоскость ![]() МНХ
ПА с двухэлементной схемой питания с БДМ.
МНХ
ПА с двухэлементной схемой питания с БДМ.
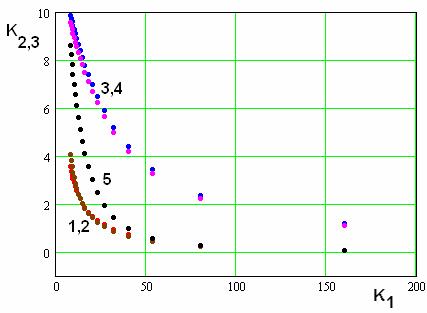
Рис. 17
Из рис. 17 видно, что точки, соответствующие первым двум схемам слились или очень близки друг другу. Отсюда следует вывод, что одноэлементная и двухэлементная схема с РДМ практически эквивалентны. Принимая во внимание большую простоту одноэлементной схемы, можно заключить, что она является безусловно лучшим по сравнению со схемой с РДМ техническим решением. Такой вывод можно считать неожиданным результатом исследования, так как исторически принято рассматривать двухэлементную схему с РДМ как шаг вперед по сравнению с одноэлементной, который должен улучшить поляризационные характеристики ПА. При этом считается, что в одноэлементной схеме недостаточно свободных параметров для одновременной реализации максимального коэффициента эллиптичности и согласования антенны даже на одной частоте. В двухэлементной схеме, на первый взгляд, этот недостаток преодолевается, так как фазовые соотношения между амплитудами ортогональных колебаний обеспечиваются выбором длин боковых плеч РДМ, а минимум коэффициента отражения выбором активных сопротивлений этих колебаний.
Тем не менее более внимательное исследование показывает, что из-за отсутствия развязки боковых плеч РДМ колебания ПА оказываются связанными друг с другом, и эту связь принципиально невозможно устранить в данной схеме. Из-за этой связи резонансные частоты системы колебаний оказываются не равными друг другу даже у ПА квадратной формы. В результате частотные зависимости ПК данной ПА приближаются к частотным зависимостям ПА с одноэлементным возбуждением и выигрыша в ПК не происходит, что подтверждают результаты ВО.
Сравнивая ПА с
одноэлементной схемой и схемой с БДМ, можно видеть, что они несравнимы, так как
вторая схема всегда имеет выигрыш по эллиптичности (ПК ![]() ), но уступает по ПК
), но уступает по ПК ![]() (см. рис. 17). При этом
особенно существенно схема с БДМ проигрывает при широких полосах рабочих
частот. Таким образом, если наиболее важным является ПК, описывающий
поляризационные характеристики ПА, то предпочтение надо отдать схеме с БДМ.
Если же более важны полоса рабочих частот и коэффициент усиления антенны, то
лучше использовать одноэлементную схему питания.
(см. рис. 17). При этом
особенно существенно схема с БДМ проигрывает при широких полосах рабочих
частот. Таким образом, если наиболее важным является ПК, описывающий
поляризационные характеристики ПА, то предпочтение надо отдать схеме с БДМ.
Если же более важны полоса рабочих частот и коэффициент усиления антенны, то
лучше использовать одноэлементную схему питания.
В заключение следует отметить, что проведенное исследование основано на представлении исследуемых ПА идеализированными моделями. Поэтому сделанные выводы справедливы в ограниченной области параметров, в которой эффекты, не учтенные при анализе, пренебрежимо малы.
Литература
1. T. Haddrell, J P. Bickerstaff, M. Phocas. Realisable GPS Antennas for Integrated Hand Held products. ION GNSS 18th International Technical Meeting of the Satellite Division, 13-16 September 2005, Long Beach, CA.
2. Wong K.L. Compact and broadband microstrip antennas // NY. John Wiley & Sons. 2002.
3. Гуткин Л.С. Проектирование радиосистем и радиоустройств. М.: Радио и связь. 1986.
4. Банков С. Е., Курушин А. А., Разевиг В. Д. Анализ и оптимизация трехмерных СВЧ структур с помощью HFSS. М.: Солон – Пресс. 2005.
5. Банков С.Е., Курушин А.А. Расчет излучаемых структур с помощью FEKO. М.: ЗАО НПП «РОДНИК». 2008.
6. Панченко Б.А., Нефедов Е.И. Микрополосковые антенны // М.: Радио и связь. 1986.
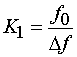 , (2)
, (2)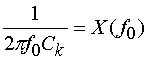 . (3)
. (3)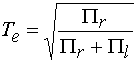 . (4)
. (4)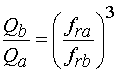 . (6)
. (6)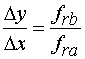 . (7)
. (7)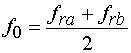 . (8)
. (8)