Исследование двух способов возбуждения меандровых линий

Исследование двух способов возбуждения меандровых линий

Г. Г. Грачёв, В. А. Калошин
Институт радиотехники и электроники им. В.А.Котельникова РАН

Получена 14 марта 2011 г.

Аннотация. В данной работе теоретически исследованы два типа возбуждения однопроводниковой меандровой линии передачи. В первом случае однопроводниковая меандровая линия возбуждается коаксиальной линией, во втором случае – волноводом. Рассмотрены два типа меандровых линий: ленточная меандровая линия с прямоугольным профилем и периодически изогнутая меандровая линия на основе круглого провода. Для проведения исследования использовались два численных метода – метод конечных элементов и метод моментов.

Ключевые слова: меандр, полосковая линия, возбуждение, ОМЛ.

Abstract. Excitation of meander strip lines and meander wired lines by smooth transition from coaxial line and by the square metallic waveguide are investigated. Investigation was conducted by finite element method and method of moments.

Keywords: meander, strip lines, excitation, SSL.

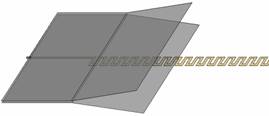
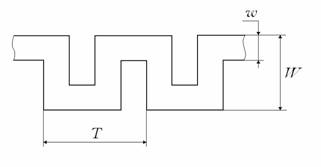
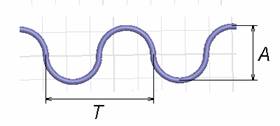
Однопроводниковая меандровая линия (ОМЛ) предложена в работе [1]. Численное исследование дисперсионных характеристик линии проведено в работе [2]. Для дальнейшего экспериментального исследования этой линии необходимо решить задачу её возбуждения. Поскольку предполагается, что основное применение ОМЛ найдёт в СВЧ диапазоне, в данной работе решается задача её возбуждения при помощи переходов от наиболее часто используемых в данном диапазоне трактов: коаксиальной линии и прямоугольного волновода. Кроме предложенной в работе [1] ленточной меандровой линии (ЛМЛ) (Рис.1а), в данной работе также рассмотрено возбуждение основной волны однопроводной периодически изогнутой меандровой линии на основе круглого провода (Рис.1б), далее в тексте - проволочная меандровая линия (ПМЛ).

а) б)

Рис. 1. Модели меандровых линий: а) ленточная меандровая линия передачи; б) проволочная меандровая линия передачи с круглым профилем.

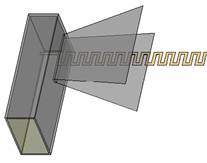
Поскольку ОМЛ является открытой линией, естественно возбуждать её с помощью плавного перехода от закрытой линии. Два таких плавных (рупорных) перехода (от коаксиальной линии и от волновода) изображены на рис. 2.

а)

б)

Рис. 2. Возбудители ленточных меандровых линий: а) рупорный возбудитель с коаксиальным входом; б) рупорный возбудитель с волноводным входом.

Как можно видеть из рис.2, коаксиальный возбудитель ЛМЛ содержит стык коаксиальный кабель - симметричная полосковая линия, отрезок симметричной полосковой линии, стык симметричная полосковая линия - симметричная полосковая меандровая линия (то есть симметричная полосковая линия передачи с меандровой лентой вместо полоска) и рупорного перехода к открытой ленточной меандровой линии передачи, представляющего собой симметричную полосковую меандровую линию с плавным увеличением расстояния между экранами.

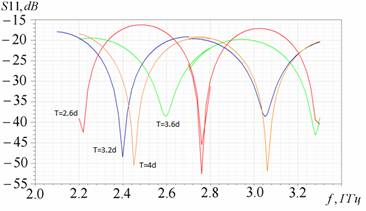
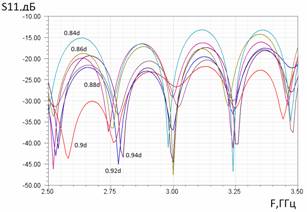
Как известно, стык коаксиальной линии и симметричной полосковой линии имеет хорошее согласование в широкой полосе частот при соблюдении условия равенства волновых сопротивлений коаксиального кабеля и симметричной полосковой линии (СПЛ). Поскольку величина волнового сопротивления симметричной полосковой меандровой линии (СПМЛ) неизвестна, для эффективного согласования стыка СПЛ- СПМЛ было проведено исследование, посвященное поиску оптимальных параметров меандровой ленты, то есть сочетания ширины полоска w, ширины линии W и периода меандра Т, при которых происходит наименьшее отражение волны от стыка. Результаты данного исследования представлены на рис.3. Исследовалась модель, содержащая отрезок СПМЛ с двумя стыками с СПЛ. Как видно из рис.3, наибольшее влияние на величину отражённой от стыка мощности оказывает ширина полоска СПМЛ. Тем не менее, в довольно широком диапазоне параметров меандра – значения периода 10мм <T< 16мм и более, и ширины меандра 12мм <W< 23мм и более, отражённая мощность не превышает -16 дБ.

Пользуясь этими результатами, нетрудно определить геометрические параметры ленты СПМЛ, близкие к оптимальным, при которых на двух стыках СПЛ-СПМЛ и СПМЛ-СПЛ в широкой полосе частот уровень отражённой мощности не превышает -30дБ, Т = 3,6d = 14,1мм; W = 5d = 19,6мм; w = 0.9d = 3.53мм, где d=3,92мм - ширина регулярного полоска СПЛ.

а)

б)

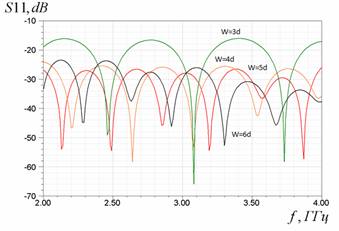
в)

Рис.3. Частотные зависимости коэффициентов отражения S11 и прохожденияS12 волны в модели из 2-х стыков :СПЛ-СПМЛ и СПМЛ-СПЛ в зависимости от: а) периода меандра Т; б) ширины wполоска СПМЛ; в) ширины Wмеандра СПМЛ. d=3,92мм - ширина полоска 50-омной СПЛ.

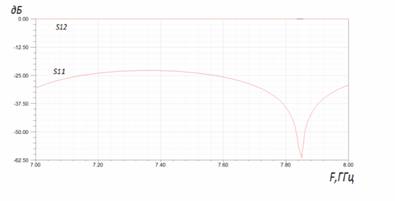
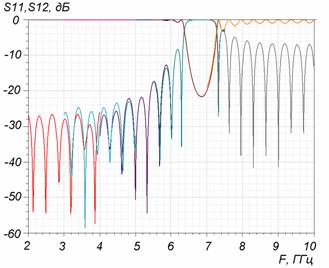
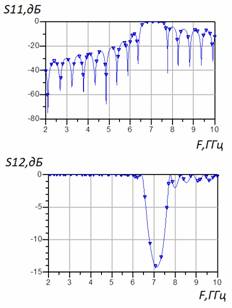
Частотные зависимости модели с этими параметрами, полученные двумя численными методами – методом конечных элементов (МКЭ) и методом моментов (ММ), приведены на рис.4. Как видно из рисунка, периодичность меандровой ленты накладывает ограничение на частотный диапазон. При увеличении частоты коэффициент отражения увеличивается и при периоде меандра, близком к половине длины волны моды, происходит почти полное её отражение. При дальнейшем уменьшении длины волны моды по сравнению с периодом меандра СПМЛ величина отражённой мощности от двух стыков уменьшается, но незначительно. Следует отметить,что результаты, полученные обоими методами (МКЭ и ММ), совпадают с графической точностью.

$Описание: G:\картинки\частотная зависимость СПЛсМ2.tif$

а) б)

Рис. 4. Частотные зависимости коэффициента отражения S11 и прохождения S12 модели из 2-х стыков: СПЛ-СПМЛ и СПМЛ-СПЛс параметрами: Т = 3,6d = 14,1мм; W = 5d = 19,6мм; w = 0.9d = 3.53мм, где d–ширина регулярного полоска СПЛ, полученные а) – МКЭ, б) ММ.

Для исследования возбуждения ЛМЛ коаксиальной линией было проведено численное моделирование в широкой полосе частот методом конечных элементов коэффициента отражения и коэффициента передачи модели, содержащей два симметрично расположенных возбудителя. Результаты расчета представлены на рис. 5. Как можно видеть из рисунка, коэффициент отражения не превышает -14дБ в широкой полосе частот - от 2,8 до 3,8 ГГц. Периодические колебания этой величины объясняются интерференцией отраженной волны от двух возбудителей. Потери на излучение также малы (коэффициент прохождения близок к единице).

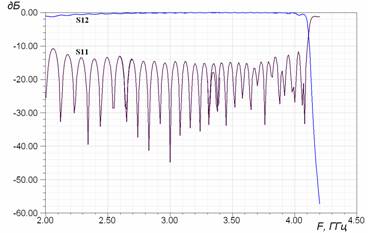
$Описание: G:\3-плоскостная линия\возбуждение меандра\rupor_100-18_v statyu.TIF$

Рис. 5. Частотная зависимость коэффициентов отражения и прохождения волны в модели, содержащей два симметричных возбудителя ЛМЛ коаксиальной линией.

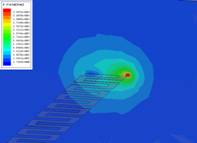
$Описание: C:\Users\Administrator\Desktop\New Folder\strip_port.tif$ $Описание: C:\Users\Administrator\Desktop\New Folder\strip_field _mean.tif$ $Описание: C:\Users\Administrator\Desktop\New Folder\strip_field _free.tif$

а) б) в)

Рис.6. Напряжённость электрического поля в плоскости, ортогональной поверхности ленты возбудителя ЛМЛ в области: а) СПЛ; б) СПМЛ; в) ЛМЛ.

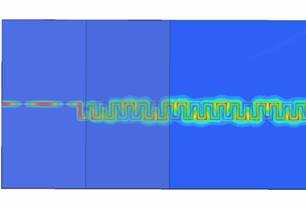
$Описание: C:\Users\Administrator\Desktop\New Folder\field1.tif$

Рис. 7. Напряжённость электрического поля в плоскости ленты возбудителя ЛМЛ.

На рис.6 и 7 представлено распределение электрического поля вдоль линии. Из рисунков видно, как преобразуется характер поля на разных участках возбудителя.

Аналогичное численное исследование проведено для возбудителя ЛМЛ с волноводным входом (рис. 2б). Результаты для частотной зависимости коэффициентов отражения и прохождения модели, содержащей два возбудителя, приведены на рис. 8.

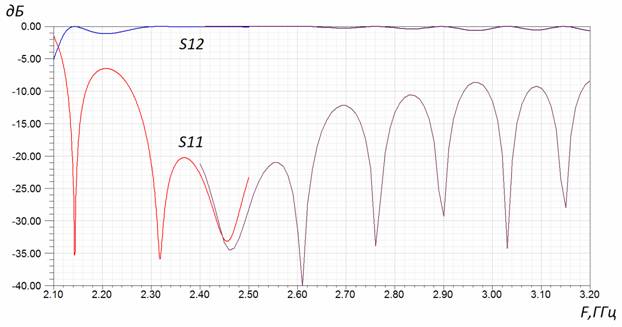
Рис. 8. Частотная зависимость коэффициентов отражения и прохождения волны в модели, содержащей два симметричных возбудителя ЛМЛ с волноводным входом.

Как видно из рисунка, полоса согласования данного возбудителя (2,3 – 2,9 ГГц по уровню -10дБ) существенно меньше, чем возбудителя с коаксиальным входом.

Аналогичное исследование было проведено также для возбуждения ПМЛ. Соответствующая модель с двумя волноводными возбудителями приведена на рис. 9. Результаты для частотной зависимости коэффициентов отражения и прохождения волны в рассмотренной модели приведены на рис.10.

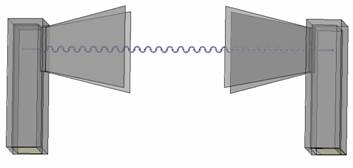
Рис. 9. Модель линии с двумя волноводными возбудителями ПМЛ.

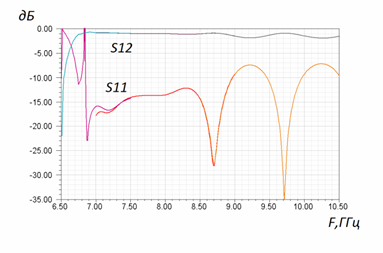
$Описание: C:\Users\Administrator\Desktop\New Folder\wg_65-10.5.tif$

Рис. 10. Частотная характеристика коэффициентов отражения и прохождения волны в модели из двух переходов прямоугольный волновод – ПМЛ.

Из рисунка видно, что в полосе частот 6,9-8,9 ГГц величина отражённой мощности не превышает -12 дБ.

На рис. 11 показана модель, состоящая из двух симметрично расположенных возбудителей ПМЛ с коаксиальным входом, и частотная зависимость, аналогичная приведённым выше. Как видно из рисунков, эффективность возбуждения ПМЛ коаксиальной линией значительно уступает эффективности возбуждения ЛМЛ. Интересно отметить, что согласование стыков СПЛ с круглым проводником - симметричная ПМЛ – СПЛ с круглым проводником сохраняется на достаточно низком уровне – величина отражённой мощности не больше – 22 дБ (рис. 13).

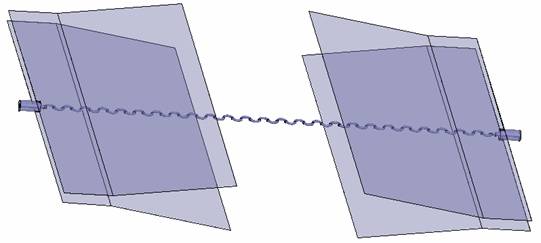
Рис. 11. Модель линии с двумя симметрично расположенными коаксиальными возбудителями ПМЛ.

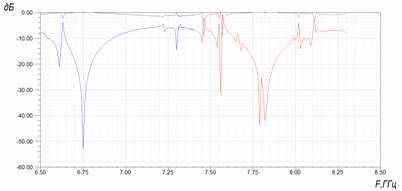
Рис.12. Частотная характеристика коэффициентов отражения и прохождения моделидвух переходов - от коаксиальной линии к ПМЛ и обратного перехода.

$Описание: C:\Users\Administrator\Desktop\New Folder\rmean_wo_rup.tif$

Рис. 13. Частотная зависимость коэффициентов отражения и прохождения стыков СПЛ с круглым проводником - симметричная ПМЛ- СПЛ с круглым проводником.

На рис.14 показано, как меняется напряженность электрического поля в рупорном переходе от СПМЛ с меандром из цилиндрического провода к ПМЛ. Видно, что структура поля в апертуре рупора отличается от структуры поля в ПМЛ, что может объяснить большие потери при возбуждении.

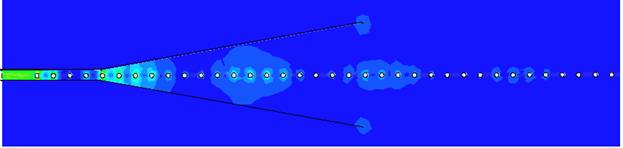
Рис. 14. Напряжённость электрического поля в сечении, ортогональном плоскости проволочной меандровой линии.

Наряду с возбудителями ПМЛ на основе проводника круглого сечения, состоящего из сопряженных полуокружностей, был исследован также возбудитель ПМЛ на основе синусоидально изогнутого провода. При этом была выбрана ПМЛ, обладающая бóльшим, по сравнению с исследованной выше ПМЛ из сопряжённых полуокружностей, замедлением.

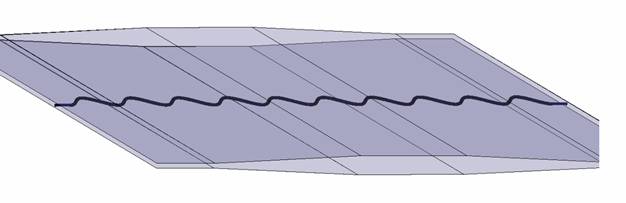
Рис. 15.Симметричные рупорные СПМЛ-переходы.

Для оценки влияния плавности перехода на величину отражённой от него мощности исследовалась модель, содержащая два симметричных рупорных СПМЛ-перехода между СПМЛ с разными расстояниями до заземляющих плоскостей, показанная на рис.15. Зависимость величины отражённой мощности S11 от частоты при различных углах α (между плоскостью меандра и одной из стенок рупора) приведена на рис. 16.

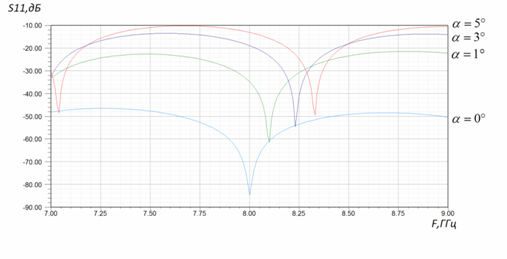
$Описание: F:\возбуждение меандра 2\New Folder\sin_mean.tif$

Рис. 16. Частотная зависимость величины отражённой мощности S11 в модели симметричных рупорных СПМЛ-переходов при разных углах α.

Как можно видеть из рис. 16, плавность перехода оказывает ключевое влияние на отражение от возбудителя, то есть уже при величине угла между плоскостью меандра СПМЛ и одной из проводящих плоскостей рупора, равной 5^о, величина отражённой мощности от двух переходов составляет -10дБ.

Заключение

Ленточная меандровая линия передачи может быть эффективно возбуждена в широком диапазоне частот с помощью плавного перехода как от коаксиальной линии, так и волновода. При этом относительная полоса согласования возбудителя ЛМЛ с волноводным входом примерно 20% по уровню -10дБ. Возбуждение ЛМЛ коаксиальной линией является более эффективным - при той же относительной полосе согласования уровень отражённой мощности не превышает -14дБ.

В отличие от ЛМЛ возбуждение ПМЛ более эффективно при помощи перехода от металлического волновода (коэффициент отражения около–12дБ при той же относительной полосе согласования). Узкая полоса согласования при коаксиальном возбуждении объясняется сильным отражением от рупорного перехода.

Работа выполнена при поддержке РФФИ, проект №10-07-00709-а.

ЛИТЕРАТУРА

1. Арсеньева Е.М, Калиничев В.И., Калошин В.А. Новые типы линий для радиосвязи в УКВ и СВЧ диапазонах волн, III Всероссийская научно-техническая конференция «Радиолокация и радиосвязь». http://jre.cplire.ru/jre/library/3conference/conf3rd.pdf, c.1031.

2. Арсеньева Е.М, Калиничев В.И., Калошин В.А. Исследование дисперсионных характеристик поверхностной волны в однопроводниковоймеандровой линии. ЖРЭ, 2011, №1 http://jre.cplire.ru/jre/jan11/4/text.pdf