УДК 004.932

МЕТОД СТЯГИВАЮЩИХСЯ ОБОЛОЧЕК ДЛЯ ВОССТАНОВЛЕНИЯ СИМВОЛЬНЫХ ИЗОБРАЖЕНИЙ

 

Д. А. Пиманкин, Б. А. Кисельман

Нижегородский государственный технический университет им. Р.Е. Алексеева

 

Получена 28 марта 2011 г.

 

Аннотация. Предложен адаптивный метод восстановления искаженных бинарных изображений, основанный на последовательном уменьшении среднего расстояния между объектом и его оболочкой. Показана возможность его применения для восстановления рукопечатных символов.

Ключевые слова: оптическое распознавание символов, восстановление изображений, морфологическая обработка, метод стягивающихся оболочек.

Abstract. The adaptive method for reconstructing of corrupted binary images, based on a successive decrease in the average distance between the object and its hull is proposed. The possibility of its application for the reconstruction of handprinted characters is demonstrated.

Keywords: optical character recognition, image reconstruction, morphological processing, method of constricting hulls.

 

Введение

Задача оптического распознавания символов вообще и рукопечатных (написанных от руки печатных символов) в частности состоит в поиске соответствия между символом и образцами (шаблонами), что зачастую существенно затруднено искажениями входных бинарных изображений. Искажения могут проявляться в виде шумов, разрывов линий и т.д. [1, 2].

Определим изображение двумерной функцией f(x, y) пространственных координат x и y. Значение функции в каждой точке, задаваемой парой координат, соответствует интенсивности изображения в этой точке. В цифровом представлении координаты x и y принимают дискретные значения: x = 0, 1, …, M – 1, y = 0, 1, …, N – 1. M и N – соответственно высота и ширина изображения в пикселях. В дальнейшем будем говорить лишь о бинарных изображениях, поэтому будем считать, что f(x, y) в каждой точке её определения может принимать лишь два значения: 1 для объекта и 0 для фона.

 

Рис. 1. Пример искажения изображения при условии F'  F.

 

Поставим в соответствие каждому пикселю изображения точку p_i = (x_i, y_i).

Определим множество точек F = {p_i : i = 1, 2, …, K_F и f(p_i) = 1}, соответствующих единичным пикселям изображения. Очевидно, что мощность этого множества K_F ≤ M ∙ N.

Под искаженным будем понимать некоторое изображение f'(x, y). Определим множество точек F' = {p_i : i = 1, 2, …, K_F' и f'(p_i) = 1}, соответствующих единичным пикселям искаженного изображения. Будем рассматривать лишь случай F'  F (и, соответственно, K_F' ≤ K_F). При этом случай F' = F (K_F' = K_F) означает отсутствие искажений.

Пример подобного искажения приведен на рис. 1.

 

Устранение искажений методами морфологической обработки

Задачей восстановления изображения является нахождение некоторой функции g(x, y), наиболее близкой в некотором смысле к функции f(x, y). Определим множество точек G = {p_i : i = 1, 2, …, K_G и g(p_i) = 1}, соответствующих единичным пикселям восстановленного изображения g(x, y).

На практике для восстановления бинарных изображений (устранения шумов, разрывов линий и т. д.) рукописных и рукопечатных символов часто используют морфологическую обработку [3, 4]. Основу морфологических методов восстановления составляют операции дилатации и эрозии [5]. Дилатация изображения A по примитиву (структурному элементу) S определяется как A  S = {z : ()_z  A ≠ }. Эрозия изображения A по примитиву S определена как A  S = {z : (S)_z  A}. Производной от операций дилатации и эрозии является операция замыкания, определенная как A  B = (A  B)  B.

Специфика задачи анализа и восстановления изображений рукописных и рукопечатных символов состоит в учёте теоретически бесконечного множества вариантов написания одного и того же символа.

Существенным недостатком применения морфологического замыкания для восстановления является то, что сложно заранее найти размер и форму оптимального примитива для этой операции. Так же тяжело проводить адаптацию под конкретные элементы символа.

Результат применения операции замыкания к искаженному бинарному изображению символа "X" приведен на рис. 2. Для восстановления использовался структурный элемент в виде окружности.

 

а)

б)

в)

Рис. 2. Результат применения операции замыкания к искаженному изображению: а – исходное изображение; б – после замыкания с окружностью радиуса 11; в – после замыкания с окружностью радиуса 21.

 

Как видно из рис. 2, результат применения операции замыкания существенно зависит от примитива, по которому проводится замыкание. В данном примере использовались примитивы в виде окружностей различного диаметра по причине инвариантности их к повороту. Можно увидеть, что чем больше радиус окружности, тем лучше сглаживание краев. В то же время происходят сильные искажения в окрестности угловых точек – сглаживание углов. Построение морфологических фильтров, оптимально восстанавливающих изображение, является нетривиальной задачей [6-8].

 

Метод стягивающихся оболочек

В данной работе предлагается альтернативный метод восстановления поврежденных изображений.

Определим множество точек H = {p_i : i = 1, 2, …, K_H}, соответствующих всем пикселям изображения. Тогда K_H = M · N. Очевидно, что F'  F  H.

Метод основан на представлении изображения символа в следующей форме:

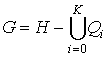                                                     _.                                                 (1)

 

Здесь Q_i – множество точек, ограниченных некоторой окружностью в системе координат 0xy.

Построим выпуклую оболочку множества точек F' – наименьший выпуклый многоугольник P, такой, что каждая точка p_i  F' находится либо на границе многоугольника P, либо в его внутренней области. Обозначим множество точек, ограниченных многоугольником P как CH. При этом F'  CH  H. Построение выпуклой оболочки производим одним из быстрых методов, например методом сканирования по Грэхему (Graham’s scan), методом обхода по Джарвису (Jarvis’s march), методом декомпозиции (devide-and-conque method) и др. [9]. В силу специфики входных данных (дискретность координат и плотность расположения точек), часть точек можно быстро отбросить, тем самым ускорив работу алгоритма.

Пусть многоугольник P имеет L вершин (p₁, p₂, …, p_L). Обозначим l_ij = (p_i, p_j) стороны многоугольника. Любой из отрезков l_ij можно представить как дугу окружности бесконечного радиуса. С учетом этого перепишем формулу (1) следующим образом:

                           _.                       (2)

 

Здесь Q_i, i = 1, 2, …, L – множества точек, ограниченных окружностями бесконечного радиуса (окружностями, вырожденными в прямые). При этом Q_i  F' = {}, i = 1, 2, …, L.

Рассчитаем преобразование расстояний (distance transform) для изображения символа. Значение преобразования расстояний в каждой точке равно наименьшему евклидову расстоянию от этой точки до ненулевого (в нашем случае единичного) пикселя [10]:

                                          , .                                      (3)

 

На рис. 3 приведено изображение символа "W" (слева) и рассчитанной для него нормированной функции d(x, y) (справа).

 

            

Рис. 3. Изображение символа "W" (слева) и соответствующей ему функции d(x, y) (справа).

 

Поставим в соответствие каждой линии l величину w, как меру среднего евклидова расстояния между символом и линией:

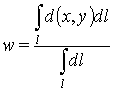                                                    .                                                (4)

Обозначим l_max линию с максимальным значением w (w_max).

Пусть Q_L+1 – множество точек, ограниченных окружностью, проходящей через концы линии l_max – точки A, B и некоторую третью точку C  F'. При этом Q_L+1  F' = {}. Точку С выберем из условия максимизации |Q_L+1  CH|.

Найдем координаты центра и радиус окружности, проходящей через точки A, B и C. Как известно, уравнение такой окружности записывается следующим образом:

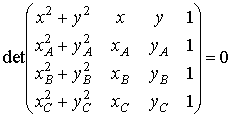                                         .                                    (5)

 

Площадь треугольника ABC:

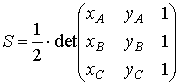                                              _.                                          (6)

 

Найдем x₀ и y₀ – координаты центра окружности:

                                        _,                                    (7)

 

                                       _.                                   (8)

 

Радиус окружности:

                                          .                                      (9)

Найденная окружность делится точками A и B на две дуги. Пусть точка B лежит в направлении обхода оболочки по часовой стрелке от точки A. Тогда обозначим за AB дугу, такую, что для любой точки C  AB можно записать:

 

                                                 .                                           (10)

 

Здесь векторное произведение v₁ × v₂ интерпретируется как определитель матрицы:

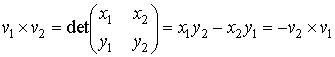                              _.                         (11)

 

Точка C делит дугу AB на две дуги AC и CB. Итак, Q_i найдено, после этого выполняется следующее преобразование:

                                                                                                      (12)

 

После этого для каждой из новых дуг (AC и CB) рассчитывается w и проводится следующая итерация. Одна итерация алгоритма иллюстрируется рис. 4.

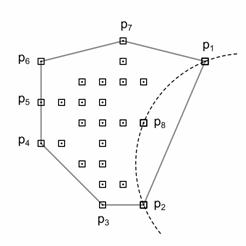
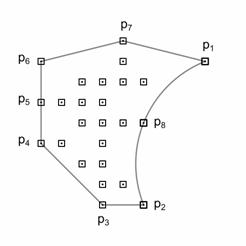
Рис. 4. Деление сегмента p₁p₂ на сегменты p₁p₈ и p₈p₂.

 

Здесь выпуклая оболочка множества F' (показана сплошной линией на рис. 4, слева) образована точками p₁, p₂, …, p₇. Часть окружности, проходящей через точки p₁, p₂ и p₈ показана пунктирной линией. На данном шаге отрезок p₁p₂ переходит в две дуги p₁p₈ и p₈p₂.

Предлагаемый метод заключается в последовательном приближении к изображению символа по мере стягивания его оболочки (метод стягивающихся оболочек, МСО). При этом на каждом шаге проявляется все больше и больше мелких элементов.

Последовательное приближение символа "W" дано на рис. 5.

 

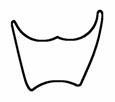
Рис. 5. Последовательное приближение изображения символа "W" его оболочками.

 

В простейшем случае алгоритм повторяется пока w_max > w_thr, где w_thr – заранее заданный фиксированный порог. Однако, значительно лучших результатов можно достичь, адаптивно изменяя порог w_thr.

Один из вариантов адаптации заключается в том, что каждому сегменту оболочки (каждой дуге) изначально присваивается некоторый уникальный идентификатор – ID. В ходе работы алгоритма, при делении сегмента на два и более, ID сохраняется для большей части сегмента, т.е. для части, имеющей большую длину. Например, для рассмотренного случая точек A, B и C, ID сегмента AB сохраняется для сегмента AC если AC / AB > T (T = 0.5 … 1). В случае, если AC / AB < T и BC / AB < T, каждой новой дуге присваивается новый ID. В ходе работы алгоритма для сегментов, сохраняющих один и тот же ID продолжительное время, используется более низкие значения порога w_thr. Такая адаптация является наиболее простой. На практике можно отслеживать изменения не только длины сегмента, но и угла его наклона, значения w и т.д.

 

Экспериментальные исследования

Для испытаний использовались искаженные бинарные изображения символов размером 512×512 пикселей. Для восстановления применялся алгоритм с использованием двух порогов: w_thr1 = 4.5 и w_thr2 = 0.25. Низкий порог применялся для дуг со временем жизни ID более J итераций, высокий – для дуг со временем жизни ID менее J итераций.

Результаты восстановления символов с различными топологическими свойствами [11] (число Эйлера для символа "X" равно 1, для символа "A" – 0) при помощи операции замыкания и предлагаемого метода приведены на рис. 6.

 

а)	б)	в)
г)	д)	е)

Рис. 6. Сравнение результатов восстановления: а, г – искаженные изображения; б, д – изображения, восстановленные при помощи операции замыкания (r = 17); в, е – изображения, восстановленные при помощи МСО.

 

Как видим, предлагаемый метод более эффективно устранил дефекты, при этом сохранилась форма в окрестностях угловых точек.

 

Заключение

Представленный метод позволяет рассматривать изображение в различных масштабах детализации. Сначала изображение грубо представляется описывающей выпуклой областью. С каждой новой итерацией мы имеем все более детальное представление изображения.

Алгоритмическая реализация допускает достаточно гибкую настройку в зависимости от специфики входных данных.

Преимущества метода. Во-первых, на каждом шаге нам известна вся предыстория, мы можем активно управлять дальнейшим процессом – адаптировать его под конкретный элемент обрабатываемого символа путем изменения порогов. Во-вторых, метод не использует понятие связности пикселей, так как работает уже не с самими пикселями, а с точками на плоскости.

Недостатком метода является существенно меньшая скорость работы по сравнению, например, с выполнением морфологического замыкания. Введение ряда приближений и «послаблений», возможно,  позволит сократить вычислительные затраты.

 

Литература

 

1.     Jyotirmoy Banerjee. Contextual Restoration of Severely Degraded Document Images / Jyotirmoy Banerjee, Anoop M. Namboodiri, C. V. Jawahar // IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2009). 2009. P. 517-524.

2.     Roy. K. A System for Joining and Recognition of Broken Bangla Numerals for Indian Postal Automation / K. Roy, U. Pal and B. B. Chaudhuri // 4th Indian Conference on Computer Vision, Graphics and Image Processing. 2004. P. 581-586.

3.     Donggang Yu. Reconstruction of broken handwritten digits based on structural morphological features / Donggang Yu, Hong Yan // Pattern Recognition 34(2). 2001. P. 235-254.

4.     Worapoj Peerawit. The Utilization of Closing Algorithm and Heuristic Information for Broken Character Segmentation / Worapoj Peerawit, Warat Yingsaeree and Asanee Kawtrakul // IEEE conference on Cybernatics and Intelligent Systems (CIS2004). 2004. Singapore.

5.     Шапиро Л. Компьютерное зрение. // Л. Шапиро, Дж. Стокман / Пер. с англ. – М.: Бином. Лаборатория знаний. 2006.

6.     Serra J. Image Analysis and Mathematical Morphology / Serra, J. // Academic Press, New York. 1982.

7.     Shih F. Y. Image Processing and Mathematical Morphology: Fundamentals and Applications / F. Y. Shih // CRC Press. 2009.

8.     Shih F. Y. Image Processing and Pattern Recognition: Fundamentals and Techniques / F. Y. Shih // IEEE Press. 2010.

9. Кормен Томас Х. Алгоритмы: построение и анализ, 2-е издание / Кормен Томас Х., Лейзерсон Чарльз И., Ривест Рональд Л., Штайн Клиффорд // Пер. с англ. – М.: Издательский дом "Вильямс". 2009.

10.   Szeliski R. Computer Vision: Algorithm and Applications (September 3, 2010 draft) / R. Szeliski.

11.   Gonzalez Rafael C. Digital Image Processing, 3rd edition / Rafael C. Gonzalez, Richard E. Woods // Pearson/Prentice Hall. 2008.