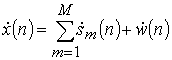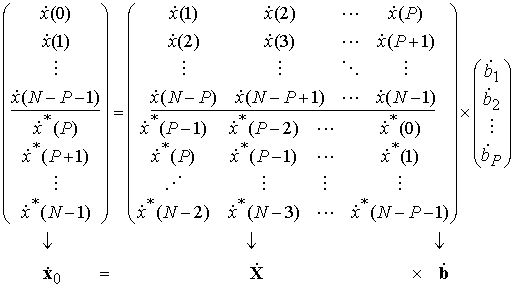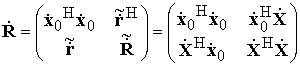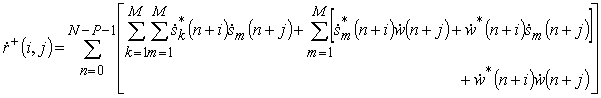УДК 621.396.677
КОГЕРЕНТНАЯ ОБРАБОТКА ДАННЫХ В ЗАДАЧАХ СПЕКТРАЛЬНОГО АНАЛИЗА РАДИОЛОКАЦИОННЫХ СИГНАЛОВ СО СВЕРХРАЗРЕШЕНИЕМ
Д. С. Григорян
Лаборатория проблем обработки радиолокационной информации военной академии войсковой ПВО ВС РФ, Смоленск
Получена 23
февраля 2012 г.
Аннотация. Установлено, что при достаточно больших мощностях сигналов, конечные значения отношений сигнал/шум в элементах корреляционных матриц не зависят от способа накопления сигнала. Исследовано влияние величины относительного интервала анализа на относительную норму вектора возмущений весовых коэффициентов и определено ее граничное значение. Определено, что при одном и том же порядке модели относительная норма вектора возмущений весовых коэффициентов при использовании предварительной когерентной обработки данных внутри выборки существенно ниже, чем норма вектора возмущений весовых коэффициентов при использовании исходных авторегрессионных методов цифрового спектрального анализа. Теоретически определено и доказано экспериментально, что эффективность сверхразрешения при одинаковых отношениях сигнал/шум зависит от относительного интервала анализа вне зависимости от выбранного метода обработки данных. Показано очевидное с точки зрения вычислительных затрат преимущество когерентных методов линейного предсказания с прореживанием по сверхразрешению гармонических сигналов по сравнению с исходными методами спектрального анализа.
Ключевые слова: сверхразрешение, линейное предсказание, вектор весовых коэффициентов, обусловленность, спектральная функция.
Abstract. It is established that at enough big power of signals, final values of relations a signal/noise in elements of correlation matrixes don't depend on a way of accumulation of a signal. Influence of size of a relative interval of the analysis on relative norm of a indignations vector of weight factors is investigated and its boundary value is defined. It is defined that at the same order of model relative norm of a indignations vector of weight factors at use of preliminary coherent data processing in sample essentially more low, than norm of a vector of indignations of weight factors at use initial autoregressive methods of the digital spectral analysis. It is theoretically defined and proved experimentally that efficiency of the superresolution at identical relations a signal/noise depends on a relative interval of the analysis without dependence from the chosen method of data processing. Obvious advantage from the point of view of computing expenses of coherent methods of a linear prediction with прореживанием under the superpermission of harmonious signals in comparison with initial methods of the spectral analysis is shown.
Keywords: superresolution, linear prediction, weight vector, conditionality, spectral function.
Введение
При проектировании современных радиолокационных систем различного назначения, как бортовых, так и наземных, большое внимание уделяется вопросам повышения их разрешающей способности по различным координатам и параметрам. Не во всех случаях удается достигнуть требуемых показателей разрешающей способности по угловым координатам из-за ограниченных размеров антенн или по частоте Доплера из-за ограниченности интервала наблюдения. Дополнительное увеличение размеров апертуры связано с техническими трудностями, а увеличение длительности выборки во многих случаях приводит к «размазыванию» спектра сигнала вследствие более быстрого изменения частот Доплера по сравнению с длительностью наблюдения. При обработке сигналов в когерентно-импульсных режимах работы локаторов разрешение по дальности ограничено шириной спектра радиосигналов, которая зачастую не может быть увеличена из-за аппаратных ограничений.
Приведенные противоречия заставляют многих исследователей искать способы сверхразрешения или по-другому «сверхрелеевского» разрешения радиолокационных сигналов. К настоящему времени в открытой зарубежной печати опубликован широкий спектр работ, описывающих различные подходы к сверхразрешению, которые весьма удачно обобщены в [1, 2]. Среди отечественных работ известны статьи Ширмана [3], Варюхина [4, 5], Курикши [6], Шинакова и Сперанского [7, 8], Фальковича и Коновалова [9], Черемисина [10, 11], Ермолаева [12], Дрогалина [13], Леховицкого [14], Слюсара [15] и многих других [16–29], исследующих тематику сверхразрешения.
Одним из известных путей сверхразрешения, который может быть применим к радиолокационным сигналам, является путь применения параметрических методов цифрового спектрального анализа, обобщенных в работах Марпла [1] и Стоицы [2]. Их достоинством считается эффект сверхразрешения, достигаемый при сравнительно небольших вычислительных затратах, не требующих перебора разных комбинаций параметров математических моделей сигналов для достижения заданного критерия эффективности. Однако эффект «расщепления» спектральных линий при обработке параметрическими методами зависит в первую очередь от отношения «сигнал/шум» (ОСШ), определяемого мощностью источников и от длины выборки, которые в условиях наблюдения радиолокационных сигналов не всегда достигают требуемых для сверхразрешения величин. Во вторую очередь сверхразрешение параметрических методов зависит от способов формирования матриц данных, обоснование которых в цифровом спектральном анализе до сих пор носит эмпирический характер.
Для достижения высокой (сверхрелеевской) разрешающей способности спектрального анализа в радиолокации необходимы методы обработки ограниченных последовательностей данных, обеспечивающие при одинаковых ОСШ и порядке модели авторегрессии наилучшее разрешение и при этом отличающиеся сравнительно малыми вычислительными затратами.
Целью статьи является обоснование границы сверхразрешения для значений относительной нормы возмущений вектора весовых коэффициентов и на ее основе обоснование методов обработки данных в частотной, временной и пространственной областях, улучшающих по сравнению с известными авторегрессионными методами спектрального анализа разрешающую способность при одних и тех же ОСШ и порядках модели авторегресии.
Исходный подход линейного предсказания
Большинство параметрических методов цифрового спектрального анализа, такие, начиная от уравнений Юла–Уолкера и заканчивая методами MUSUC и ESPRIT, определяют некую последовательность весовых коэффициентов, которые напрямую или с точностью до постоянного комплексного множителя можно поставить в соответствие вектору весовых коэффициентов (ВВК) авторегресии. В линейной комбинации с данными ВВК предсказывает значение следующего отсчета по предыдущим отсчетам.
Рассмотрим одну из эффективных процедур параметрического авторегрессионного спектрального анализа – метод линейного предсказания вперед-назад [1]. Представим выборку из N (n=0..N–1) дискретных отсчетов аддитивной смеси M (m=1..M) гармонических сигналов и шума в виде
где ![]() – n-й отсчет m-го гармонического сигнала;
– n-й отсчет m-го гармонического сигнала;
![]() ,
,
![]() – начальная фаза и частота m-го источника;
– начальная фаза и частота m-го источника;
![]() –
шаг дискретизации сигналов по времени;
–
шаг дискретизации сигналов по времени;
![]() – комплексное значение шума n-го отсчета.
– комплексное значение шума n-го отсчета.
Для порядка модели авторегрессии P<N объединим данные таким образом, чтобы сформировать систему уравнений линейного предсказания вперед-назад вида
в которой где ![]() –
вектор свободных членов;
–
вектор свободных членов; ![]() – матрица данных;
– матрица данных; ![]() – вектор весовых коэффициентов (ВВК)
авторегресии. Решения системы (2) определим по методу наименьших
квадратов из системы
– вектор весовых коэффициентов (ВВК)
авторегресии. Решения системы (2) определим по методу наименьших
квадратов из системы
или из эквивалентной системы
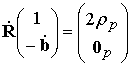 ,
,
где
–полная корреляционная матрица (КМ)
системы размерностью P+1×P+1; ![]() и
и ![]() – КМ и опорный вектор (ОВ) системы
уравнений линейного предсказания;
– КМ и опорный вектор (ОВ) системы
уравнений линейного предсказания; ![]() – оператор эрмитового
транспонирования;
– оператор эрмитового
транспонирования; ![]() – дисперсия шумов.
– дисперсия шумов.
Вектор весовых
коэффициентов ![]() определяет спектральную функцию
частоты
определяет спектральную функцию
частоты
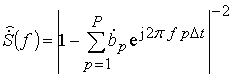 , (5)
, (5)
в основе которой лежит характеристический полином
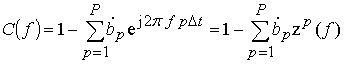 (6)
(6)
относительно аргумента ![]() . Корни характеристического полинома
. Корни характеристического полинома ![]() ,
, ![]() ,…,
,…, ![]() определяют оценки частот
определяют оценки частот ![]() , среди которых M могут принадлежать
подпространству сигналов, а остальные N–M
шумовому подпространству.
, среди которых M могут принадлежать
подпространству сигналов, а остальные N–M
шумовому подпространству.
Эффект накопления в корреляционной матрице
Элементы КМ можно определить как
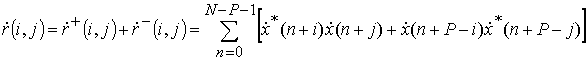 , (7)
, (7)
где i=0..P, j=0..P; ![]() –
оператор транспонирования;
–
оператор транспонирования; ![]() – корреляционные моменты, определяемые прямыми отсчетами при
предсказании вперед (прямые корреляционные моменты);
– корреляционные моменты, определяемые прямыми отсчетами при
предсказании вперед (прямые корреляционные моменты); ![]() – корреляционные моменты, определяемые обратными
комплексно-сопряженными отсчетами при предсказании назад (обратные
корреляционные моменты). Рассмотрим
элементы прямой КМ, которые с учетом (1) могут быть
записаны в виде
– корреляционные моменты, определяемые обратными
комплексно-сопряженными отсчетами при предсказании назад (обратные
корреляционные моменты). Рассмотрим
элементы прямой КМ, которые с учетом (1) могут быть
записаны в виде
Операция
(4) по вычислению корреляционного момента ![]() эквивалентна операции фазового
детектирования, характерного для работы корреляторов, а для диагональных
элементов – эквивалентна квадратичному амплитудному детектированию. Шум
эквивалентна операции фазового
детектирования, характерного для работы корреляторов, а для диагональных
элементов – эквивалентна квадратичному амплитудному детектированию. Шум ![]() элемента КМ будет определяться вторым и третьим слагаемыми уравнения (8).
Второе слагаемое, представляющее сумму произведений M сигналов источников и шума, является комбинационным
шумом, представляющим собой мультипликативную смесь гармонических сигналов и
шума. Третье слагаемое задает шум, определяемый произведением шумов. При спектральном
анализе сигналов по частоте и пространству сверхразрешение в пределах
релеевского элемента разрешения имеет место при достаточно высоких ОСШ от 20 дБ
и выше [1, 17, 28,
29]. Для условий некогерентного накопления при высоких ОСШ
комбинационный шум можно считать много больше третьего слагаемого [31, с. 250].
Такое допущение позволяет пренебречь третьим слагаемым уравнения (8), так как,
например это показано в [18]. Первое слагаемое (8) определяет полезную
информацию в элементах КМ. Амплитуды сигналов корреляционного момента
элемента КМ будет определяться вторым и третьим слагаемыми уравнения (8).
Второе слагаемое, представляющее сумму произведений M сигналов источников и шума, является комбинационным
шумом, представляющим собой мультипликативную смесь гармонических сигналов и
шума. Третье слагаемое задает шум, определяемый произведением шумов. При спектральном
анализе сигналов по частоте и пространству сверхразрешение в пределах
релеевского элемента разрешения имеет место при достаточно высоких ОСШ от 20 дБ
и выше [1, 17, 28,
29]. Для условий некогерентного накопления при высоких ОСШ
комбинационный шум можно считать много больше третьего слагаемого [31, с. 250].
Такое допущение позволяет пренебречь третьим слагаемым уравнения (8), так как,
например это показано в [18]. Первое слагаемое (8) определяет полезную
информацию в элементах КМ. Амплитуды сигналов корреляционного момента ![]() будут определяться суммой
будут определяться суммой
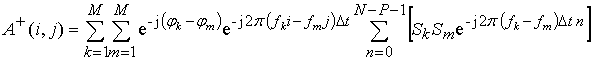 , (9)
, (9)
Суммируя по n в правой части (9) получим сумму геометрической прогрессии и после несложных операций формула (9) преобразуется к виду
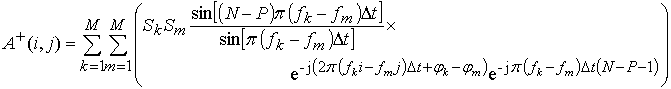 . (10)
. (10)
В диагональных элементах КМ ![]() при
при ![]() амплитуда
сигнала будет складываться из суммы амплитуд отдельных источников при
амплитуда
сигнала будет складываться из суммы амплитуд отдельных источников при ![]() и суммы комбинационных членов при
и суммы комбинационных членов при ![]() , определяемых из (10) при
, определяемых из (10) при ![]() . Выполнив аналогичные преобразования, получим
выражения для амплитуды элементов обратной КМ
. Выполнив аналогичные преобразования, получим
выражения для амплитуды элементов обратной КМ
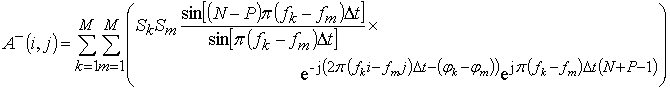
Рассмотрим для прямой КМ m-й элемент комбинационного шума из (8)
![]() ,
,
элементы которого после преобразования представим в виде вещественной и мнимой частей как
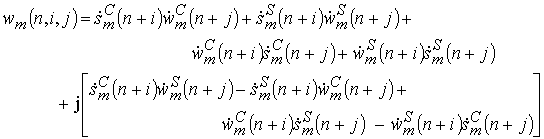 .
.
Поскольку
величина ![]() состоит из суммы некоррелированных случайных
величин, то ее дисперсия, будет определяться суммой дисперсий случайных
величин. Обозначим текущую фазу m-й гармоники как
состоит из суммы некоррелированных случайных
величин, то ее дисперсия, будет определяться суммой дисперсий случайных
величин. Обозначим текущую фазу m-й гармоники как ![]() . Тогда дисперсию вещественной
и мнимой частей m-го элемента
комбинационного шума можно представить в виде
. Тогда дисперсию вещественной
и мнимой частей m-го элемента
комбинационного шума можно представить в виде
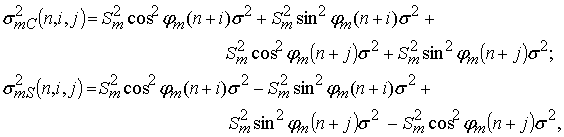
откуда получим
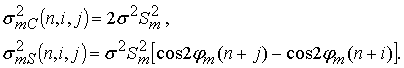 (11)
(11)
Из (11) следует, что для
диагональных элементов КМ комбинационный шум вещественный. С удалением от
главной диагонали КМ дисперсия мнимой части шума возрастает. Кроме того,
учитывая (4) можно сделать вывод, что при увеличении количества источников
комбинационный шум также возрастает. Для количества источников равных M после несложных операций суммирования
в ![]() элементе прямой и перевернутой КМ получим
вещественную и мнимую части дисперсии комбинационного шума
элементе прямой и перевернутой КМ получим
вещественную и мнимую части дисперсии комбинационного шума
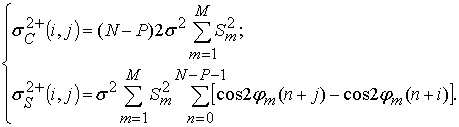 (12)
(12)
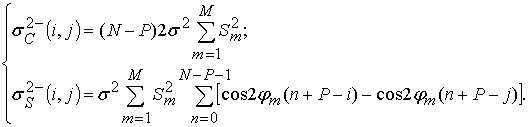 (13)
(13)
Для простоты рассмотрим ОСШ в диагональных элементах КМ для случая одной гармоники. Тогда полезная амплитуда гармоники будет определена как
![]() .
.
Дисперсия шума в произвольном элементе КМ будет иметь вид
![]() .
.
Отношение сигнал/шум по мощности в диагональных элементах КМ будет определяться как
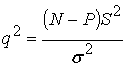 , (14)
, (14)
откуда следует, что в случае одного источника при достаточно высокой мощности сигнала, с учетом принятых выше допущений, ОСШ в диагональных элементах подчиняется законам когерентного накопления [31].
В
случае нескольких источников дисперсии вещественной и мнимой частей комбинационного
шума растут пропорционально увеличению количества источников притом, что амплитуда
каждого из источников увеличивается, как и в случае с одним источником, в ![]() раз. Это отчасти объясняет тот факт,
при увеличении количества источников в пределах релеевского элемента условия их
разрешения ухудшаются [18] пропорционально увеличению их количества, так как
ОСШ для M источников в диагональном элементе можно приблизительно
определить как
раз. Это отчасти объясняет тот факт,
при увеличении количества источников в пределах релеевского элемента условия их
разрешения ухудшаются [18] пропорционально увеличению их количества, так как
ОСШ для M источников в диагональном элементе можно приблизительно
определить как
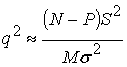 . (15)
. (15)
Необходимое условие сверхразрешения
В одной из своих работ Савинов [22], основываясь на известном из линейной
алгебры условии единственности решений системы линейных уравнений [30], записал
для относительной нормы ![]() возмущений
возмущений ![]() вектора весовых коэффициентов (ВВК)
сигнального подпространства
вектора весовых коэффициентов (ВВК)
сигнального подпространства ![]() неравенство
вида
неравенство
вида
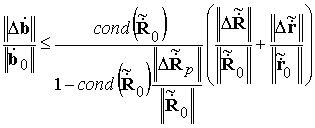 ,
(16)
,
(16)
в
котором ![]() – корреляционная матрица (КМ) сигнального
подпространства;
– корреляционная матрица (КМ) сигнального
подпространства;
![]() –
возмущение КМ сигнального подпространства;
–
возмущение КМ сигнального подпространства; ![]() –
опорный вектор (ОВ) сигнального подпространства;
–
опорный вектор (ОВ) сигнального подпространства; ![]() –
возмущение ОВ сигнального подпространства;
–
возмущение ОВ сигнального подпространства; ![]() –
число обусловленности КМ сигнального подпространства;
–
число обусловленности КМ сигнального подпространства;
Выборочные оценки КМ и ОВ представляют сумму КМ и ОВ сигнального подпространства и их возмущений, т. е.
![]() и
и ![]() .
.
Неравенство (17) устанавливает условие единственности решений для относительной нормы возмущений ВВК подпространства сигналов, что можно считать необходимым условиям для сверхразрешения вообще. Однако это далеко не достаточное условие для сверхразрешения.
При наличии шумов система (3) будет иметь вид
![]() , (17)
, (17)
откуда [29, 30] получим возмущения ВВК в виде
![]() (18)
(18)
где ![]() –
единичная матрица размером
–
единичная матрица размером ![]() .
.
Из (18) следует, что чем меньше главный
определитель матрицы ![]() , тем меньше матрица
, тем меньше матрица ![]() и тем меньше возмущения
и тем меньше возмущения ![]() . Тем не менее, с точки зрения сверхразрешения
мы рассматриваем относительную норму возмущений ВВК, которая равна отношению
. Тем не менее, с точки зрения сверхразрешения
мы рассматриваем относительную норму возмущений ВВК, которая равна отношению ![]() нормы возмущений ВВК к норме ВВК подпространства сигналов, определяемого
как
нормы возмущений ВВК к норме ВВК подпространства сигналов, определяемого
как ![]() . В этом случае при вычислении отношения
. В этом случае при вычислении отношения ![]() норм определители матриц подпространства сигналов сокращаются. Поэтому
к положительному влиянию на сверхразрешение числа обусловленности
корреляционной матрицы подпространства сигналов следует относиться несколько по
другому, а не так как это сделано в [22]. Это означает, что для любого метода
обработки данных вне зависимости от числа обусловленности корреляционной
матрицы подпространства сигналов, нижняя граница сверхразрешения для отношения
норм
норм определители матриц подпространства сигналов сокращаются. Поэтому
к положительному влиянию на сверхразрешение числа обусловленности
корреляционной матрицы подпространства сигналов следует относиться несколько по
другому, а не так как это сделано в [22]. Это означает, что для любого метода
обработки данных вне зависимости от числа обусловленности корреляционной
матрицы подпространства сигналов, нижняя граница сверхразрешения для отношения
норм ![]() будет одинакова.
будет одинакова.
Чтобы убедиться, что
лучшая обусловленность КМ подпространства сигналов все же улучшает условия
сверхразрешения, можно проанализировать уравнение (18), из которого видно, что
чем больше главный определитель ![]() , тем меньше
, тем меньше ![]() . Отсюда следует, что разрешающая способность напрямую зависит
от точки пересечения текущего отношения
. Отсюда следует, что разрешающая способность напрямую зависит
от точки пересечения текущего отношения ![]() с
неким граничным отношением
с
неким граничным отношением ![]() , суть которого будет
пояснена ниже.
, суть которого будет
пояснена ниже.
Как показано в [32]
выборочная корреляционная матрица ![]() и опорный вектор
и опорный вектор ![]() определяются как
определяются как
![]() , (20)
, (20)
где
![]() =
=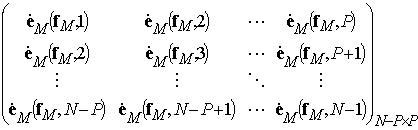 , (21)
, (21)
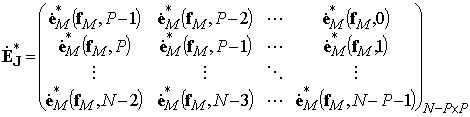 (22)
(22)
– блочные ганкелева и тёплицева (прямая и обратная) матрицы комплексных экспонент (комплексных характеристик фильтров), характеризующих изменение фазы гармоник с разными частотами от одного дискретного отсчета к другому при выполнении процедуры оценивания вперед-назад;
![]() , (23)
, (23)
![]() (24)
(24)
– векторы столбцы опорных комплексных экспонент, формирующих опорный вектор;
![]() –
вектор частот M источников;
–
вектор частот M источников;
![]() –
вектор комплексных экспонент;
–
вектор комплексных экспонент;
![]() – вектор комплексных амплитуд источников;
– вектор комплексных амплитуд источников;
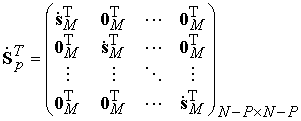 –
блочная
–
блочная ![]() матрица векторов амплитуд.
матрица векторов амплитуд.
Из анализа (19)–(24) видно, что обусловленность КМ подпространства сигналов в большей степени определяется матрицами экспонент (21) и (22), которые зависят от способа обработки данных.
Обусловленность КМ
сигнального подпространства, определяется обусловленностью матрицы ![]() . Поскольку отсчеты удалены друг от друга
на один элемент, при малых порядках модели обусловленность КМ подпространства
сигналов будет невысокая. Для снижения обусловленности КМ сигнального
подпространства в работе [32] предлагается применить методы прореживания
отсчетов данных с когерентным накоплением, суть которых поясняется ниже.
. Поскольку отсчеты удалены друг от друга
на один элемент, при малых порядках модели обусловленность КМ подпространства
сигналов будет невысокая. Для снижения обусловленности КМ сигнального
подпространства в работе [32] предлагается применить методы прореживания
отсчетов данных с когерентным накоплением, суть которых поясняется ниже.
Методы предварительной обработки данных с когерентным накоплением
Выборку ![]() из N значений можно разбить на Q субвыборок из N1 = N /Q отсчетов (рис.1). Когерентно суммируя
отсчеты в пределах каждой q-й
субвыборки с помощью операции
из N значений можно разбить на Q субвыборок из N1 = N /Q отсчетов (рис.1). Когерентно суммируя
отсчеты в пределах каждой q-й
субвыборки с помощью операции
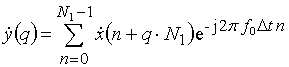 , (25)
, (25)
получим Q значений отсчетов вторичной выборки, где ![]() номер отсчета прореженной выборки;
номер отсчета прореженной выборки; ![]() – резонансная частота полосовых фильтров
предварительной обработки (ФПО). Резонансная частота ФПО
– резонансная частота полосовых фильтров
предварительной обработки (ФПО). Резонансная частота ФПО ![]() , определяющая импульсную характеристику вида
, определяющая импульсную характеристику вида
![]() , выбирается равной частоте максимума
дискретного преобразования Фурье (ДПФ) всей выборки
, выбирается равной частоте максимума
дискретного преобразования Фурье (ДПФ) всей выборки ![]() .
.
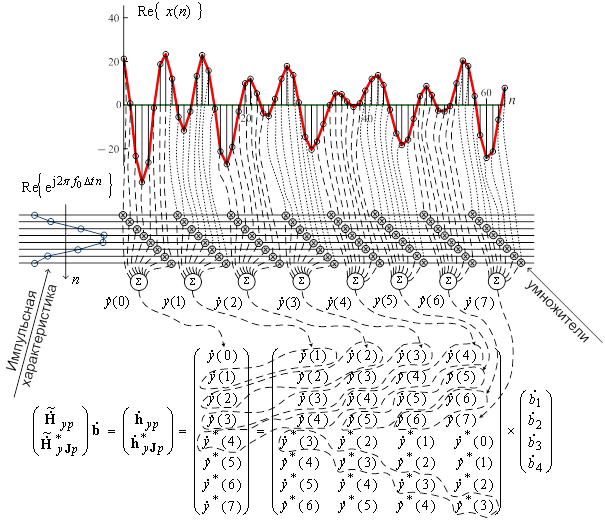
Рис. 1. Схема формирования матриц данных из выборки размером 64 отсчета с прореживанием до 8 отсчетов с когерентным накоплением по 8 отсчетов.
Комплексная частотная характеристика (КЧХ) ФПО будет определяться как
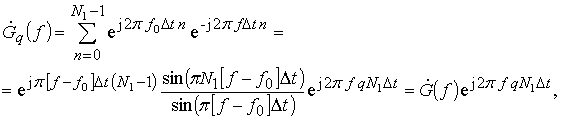 (26)
(26)
где 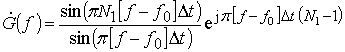 –
часть КЧХ, идентичная для всех ФПО. Амплитудно-частотные характеристики (АЧХ)
ФПО одинаковые и имеют вид функции sinN1x/sinx, а отличия фазо-частотных характеристик
(ФЧХ) определяются задержками
–
часть КЧХ, идентичная для всех ФПО. Амплитудно-частотные характеристики (АЧХ)
ФПО одинаковые и имеют вид функции sinN1x/sinx, а отличия фазо-частотных характеристик
(ФЧХ) определяются задержками ![]() .
.
По аналогии с системой (2) отсчеты вторичной выборки в векторно-матричной форме могут быть объединены в систему
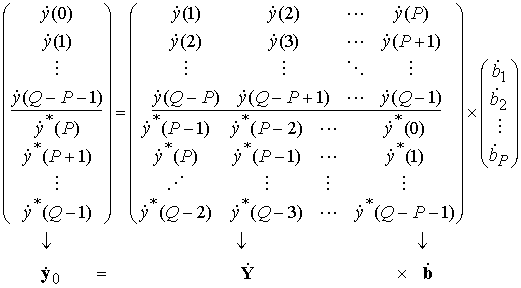 (27)
(27)
откуда
![]() , (28)
, (28)
или из эквивалентной системы
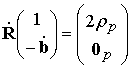 ,
,
где
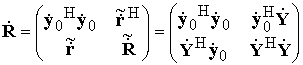 (29)
(29)
–полная КМ системы размерностью
P+1×P+1; ![]() и
и ![]() – КМ и ОВ системы уравнений когерентного
метода линейного предсказания.
– КМ и ОВ системы уравнений когерентного
метода линейного предсказания.
В [32] показано, что при когерентной обработке данных КМ подпространства сигналов будет иметь вид
![]() ,
(30)
,
(30)
где
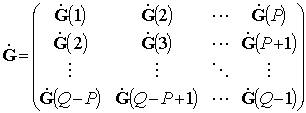 ,
,
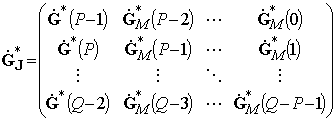
– блочные ![]() ганкелева
и тёплицева матрицы КЧХ ФПО, характеризующие изменение фазы гармоник с разными
частотами от одного прореженного отсчета к другому при выполнении процедуры
предсказания вперед-назад;
ганкелева
и тёплицева матрицы КЧХ ФПО, характеризующие изменение фазы гармоник с разными
частотами от одного прореженного отсчета к другому при выполнении процедуры
предсказания вперед-назад;
![]()
– вектор ![]() -х КЧХ каналов для частот всех определяемый для частот всех источников.
-х КЧХ каналов для частот всех определяемый для частот всех источников.
Разность КЧХ разных ФПО будет определять линейную зависимость строк и столбцов, которая для КМ подпространства сигналов, определяемой из (30), меньше чем для КМ, определяемой из (19). Это обусловлено тем, что для когерентного метода имеет место прореживание отсчетов в N1 раз.
Одновременное разрешение и оценивание параметров нескольких источников возможно не только за счет различий ФЧХ отдельных каналов, но и за счет различий в АЧХ. Рассмотрим модификацию одного из амплитудных методов линейного предсказания, так называемого метода «нормирования», разработанного Абраменковым для случая оценивания сигналов двух источников [21]. Суть метода заключается в следующем. Если порядок модели равен P, то выполняются L≥P операций ДПФ (l=0.. L –1)
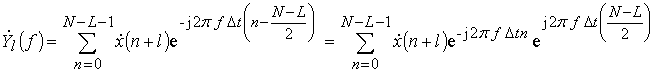 ,
,
обрабатывающих укороченные выборки
отсчетов ![]() размером N–P,
в котором экспонента
размером N–P,
в котором экспонента 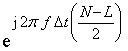 является множителем,
симметрирующим операцию ДПФ (рис.2).
является множителем,
симметрирующим операцию ДПФ (рис.2).
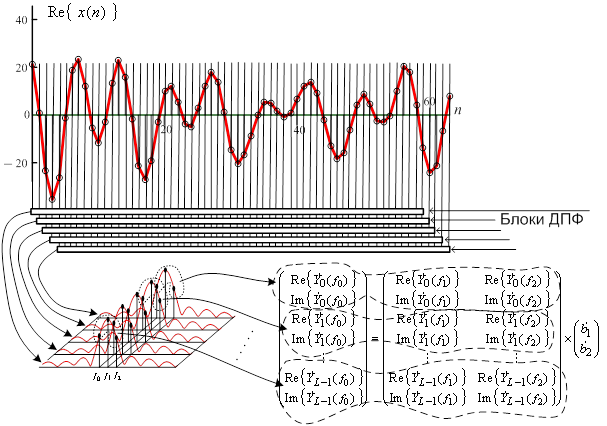
Рис.2. Схема формирования матрицы данных и системы уравнений когерентного амплитудного метода обработки данных (модифицированного метода нормирования).
Мнимая часть КЧХ фильтров такого ДПФ равна нулю, т. е. фильтры ДПФ вещественные. В окрестности пика ДПФ, выбираются P фильтров (рис. 2), КЧХ которых
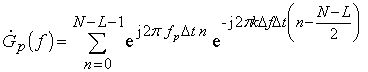 (31)
(31)
имеют резонансные частоты ![]() (p=0..P). Из отсчетов ДПФ
(p=0..P). Из отсчетов ДПФ![]() ,
соответствующих частотам
,
соответствующих частотам ![]() с номерами p=0.. P составляется система уравнений вида
с номерами p=0.. P составляется система уравнений вида
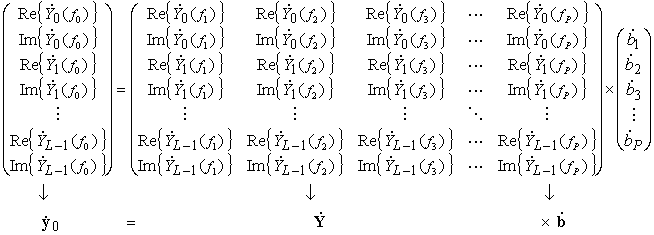
Решая данную систему уравнений методом наименьших квадратов, получим ВВК модифицированного метода нормирования вида
![]() .
.
Авторегрессионные спектральные функции (по-другому псевдоспектры) для рассмотренных методов будут иметь вид
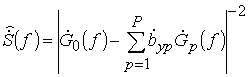 , (32)
, (32)
в которых, в
зависимости от метода предварительной обработки, КЧХ ![]() ФПО определяется
либо из (26) либо из (31).
ФПО определяется
либо из (26) либо из (31).
Оценивать частоты можно путем непосредственного анализа спектральных функций или корней характеристических полиномов фазовых методов из уравнения
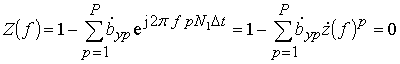 (33)
(33)
и амплитудного метода
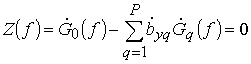 . (34)
. (34)
где ![]() –
аргумент для фазового метода.
–
аргумент для фазового метода.
Вычислив оценки частот ![]() M источников, можно вычислить амплитуды источников
путем решения обратной задачи. Для этого определяется матрица значений КЧХ каналов
на этих частотах
M источников, можно вычислить амплитуды источников
путем решения обратной задачи. Для этого определяется матрица значений КЧХ каналов
на этих частотах
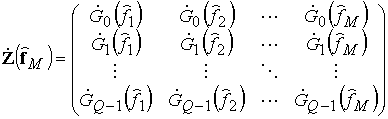 и вектор
и вектор
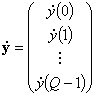
откликов ![]() каналов на
сам сигнал, связанные системой уравнений
каналов на
сам сигнал, связанные системой уравнений
![]() ,
,
откуда находим вектор комплексных амплитуд источников
![]() .
.
Для исходных методов
спектрального анализа без прореживания данных величина ![]() аргумента
характеристического полинома
аргумента
характеристического полинома ![]() будет равна единице.
будет равна единице.
Достаточное условие сверхразрешения
Для определения достаточного условия сверхразрешения рассмотрим характеристическое уравнение линейного предсказания вида
![]() , (35)
, (35)
которое для фазовых методов преобразуется к виду
![]() ,
,
где в правой скобке характеристический полином системы уравнений линейного предсказания.
Рассмотрим
теоретически интересующую нас сигнальную ситуацию, которая образована M источниками с
вектором амплитуд ![]() и частотами
и частотами ![]() . Введем также оценки частот корней
характеристического уравнения
. Введем также оценки частот корней
характеристического уравнения ![]() , в которых M оценок частот связанны с
истинными частотами источников через их возмущения
, в которых M оценок частот связанны с
истинными частотами источников через их возмущения ![]() . Подставляя значения оценок частот корней в
характеристическое уравнение (35), составим систему уравнений
. Подставляя значения оценок частот корней в
характеристическое уравнение (35), составим систему уравнений
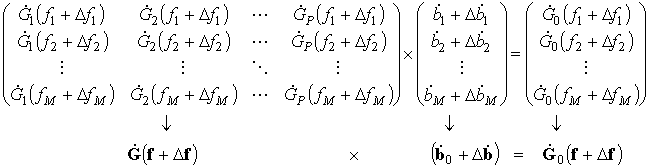 , (36)
, (36)
где ВВК подпространства сигналов определяется в общем виде как
![]() . (37)
. (37)
В случае если количество источников
не равно порядку модели, из-за вырожденности матрицы ![]() ВВК подпространства сигналов следует определять как
ВВК подпространства сигналов следует определять как
![]() ,
,
где ![]() – параметр
регуляризации, который должен быть во много раз меньше диагональных элементов
матрицы
– параметр
регуляризации, который должен быть во много раз меньше диагональных элементов
матрицы ![]() . Из системы (36) получим возмущения ВВК в виде
. Из системы (36) получим возмущения ВВК в виде
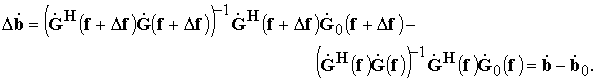
Отношение нормы вектора возмущений ВВК к норме ВВК подпространства сигналов можно записать в виде
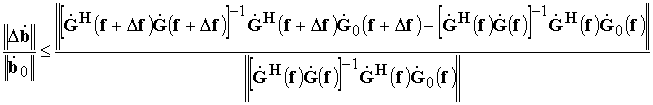 . (38)
. (38)
С другой стороны, учитывая (18), можно записать
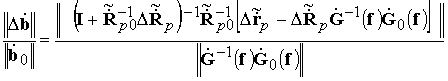 , (39)
, (39)
в котором правая часть есть
относительная норма вектора возмущений ВВК системы уравнений линейного
предсказания в зависимости от текущих возмущений КМ и ОВ. Неравенство (38) дает
возможность оценить границу возмущений ВВК при заданных случайных возмущениях
параметров ![]() , а формула (39) – оценить
каковы относительная норма возмущений ВВК при заданных возмущениях КМ и ОВ.
Если возмущения
, а формула (39) – оценить
каковы относительная норма возмущений ВВК при заданных возмущениях КМ и ОВ.
Если возмущения ![]() параметров
параметров ![]() задать статистически, то можно вычислить
среднестатистическую границу сверхразрешения для относительной нормы возмущений
ВВК усреднением (38). Сравнивая правую часть уравнения (39), возмущенной за
счет
задать статистически, то можно вычислить
среднестатистическую границу сверхразрешения для относительной нормы возмущений
ВВК усреднением (38). Сравнивая правую часть уравнения (39), возмущенной за
счет ![]() и
и ![]() , с
граничным отношением
, с
граничным отношением ![]() , определяемым из
неравенства (38), можно
аналитически определять будет ли иметь место сверхразрешение или нет.
, определяемым из
неравенства (38), можно
аналитически определять будет ли иметь место сверхразрешение или нет.
Для сравнительного анализа была рассмотрена тестовая последовательность 64-х отсчетов данных, записанных с тактовой частотой 44,1 кГц и состоящих из смеси четырех гармоник на частотах 6,25 кГц, 6,35 кГц, 6,70 кГц и 3,00 кГц. Наибольший интерес представляет зависимость граничной относительной нормы возмущений ВВК (38) от выбранного порядка модели и метода оценивания для одной и той же сигнально-шумовой ситуации. Для исходного подхода линейного предсказания вперед-назад и для когерентного подхода данная зависимость приведена на рисунках 3, 4.
С помощью системы
уравнений (36) была аналитически исследована зависимость среднестатистической
относительной нормы возмущений ВВК (38) от
выбранного порядка модели (рис. 3, 4) при условии, что СКО четырех корней
характеристического уравнения (35) не должны были превышать половины разности
частот между ближайшими источниками ![]() (
(![]() =6,25 кГц,
=6,25 кГц,
![]() =6,35 кГц).
Анализ рисунков 4 и 5 показывает, что кривые относительных возмущений ВВК
приближаются к кривой границы сверхразрешения при ОСШ свыше 30–35 дБ при
величине относительного интервала анализа свыше 0,7. Это говорит о том, что
ключевую роль для сверхразрешения играют ОСШ и относительный интервал анализа,
т. е. величина, равная отношению порядка модели авторегресии к общему
количеству данных.
=6,35 кГц).
Анализ рисунков 4 и 5 показывает, что кривые относительных возмущений ВВК
приближаются к кривой границы сверхразрешения при ОСШ свыше 30–35 дБ при
величине относительного интервала анализа свыше 0,7. Это говорит о том, что
ключевую роль для сверхразрешения играют ОСШ и относительный интервал анализа,
т. е. величина, равная отношению порядка модели авторегресии к общему
количеству данных.
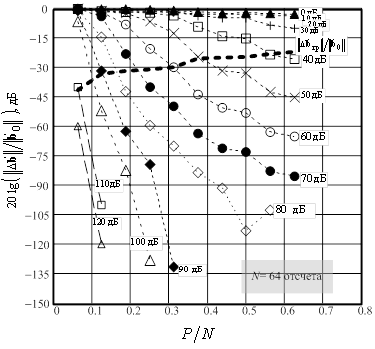
Рис.3. Зависимости отношений ![]() исходного
метода линейного предсказания вперед-назад от величины относительного интервала
анализа (отношения
исходного
метода линейного предсказания вперед-назад от величины относительного интервала
анализа (отношения ![]() порядка модели авторегресии
порядка модели авторегресии ![]() к общему числу данных)
к общему числу данных) ![]() для разных ОСШ (пунктирной линией
показана зависимость граничного отношения
для разных ОСШ (пунктирной линией
показана зависимость граничного отношения ![]() от
относительного интервала анализа).
от
относительного интервала анализа).
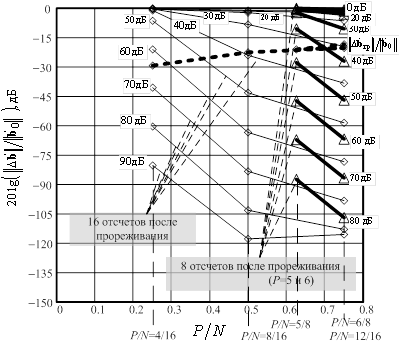
Рис.4. Зависимости отношений ![]() для
когерентного метода обработки данных с прореживанием от величины относительного
интервала анализа
для
когерентного метода обработки данных с прореживанием от величины относительного
интервала анализа ![]() для разных ОСШ (рассмотрены два
варианта прореживания с 16 отсчетами вторичной выборки и 8 отсчетами вторичной
выборки).
для разных ОСШ (рассмотрены два
варианта прореживания с 16 отсчетами вторичной выборки и 8 отсчетами вторичной
выборки).
Теоретическое исследование показывает, что граница сверхразрешения для исходных методов и для когерентных методов остается на одном и том же уровне (на рисунках обозначена пунктирной линией). При этом требуемый для сверхразрешения порядок модели когерентных методов предварительной обработки данных существенно ниже, чем порядок модели, требуемый для сверхразрешения исходными методами. В анализируемом случае общее число данных составляло 64. Было рассмотрено прореживание до 16-и отсчетов вторичной выборки (рис.4) с порядками модели 4, 8 и 12 (относительный интервал анализа от 4/16 до 12/16), и до 8-и отсчетов вторичной выборки с порядками модели 5 и 6 (относительный интервал анализа от 5/8 и 6/8). Для исходного варианта без прореживания то же самое разрешение достигалось при порядке модели свыше 40 (относительный интервал анализа от 40/64, рис.3). Большой порядок модели означает большую размерность КМ. Когерентные и исходные методы для обеспечения одного и того же относительного интервала авторегрессионного анализа используют разные порядки модели, которые для когерентных методов существенно ниже. При использовании же более низких порядков модели в исходных подходах, они существенно проигрывают когерентным методам в разрешающей способности. Поэтому преимущество когерентных методов в данном случае очевидно.
Отсюда следует вывод, что если в радиолокационных системах при работе по нескольким целям возникает задача сверхразрешения сигналов по пространству, частоте или дальности, то предпочтительнее использовать когерентные методы предварительной обработки данных с прореживанием, позволяющие существенно уменьшить порядок модели авторегресии до количества целей, параметры которых подлежат измерению, а сами цели селекции. Однако главным является то, что эффективность сверхразрешения зависит от относительного интервала анализа. Поэтому искусство спектральной обработки в радиолокации заключается в том, чтобы сформировать матрицу данных низкого порядка, обеспечивая максимально возможный при этом относительный интервал анализа.
Некоторые результаты экспериментов с тестовыми выборками
В ходе сравнительного анализа была протестирована последовательность 64-х отсчетов данных, состоящих из смеси четырех гармоник на частотах 6,25 кГц, 6,35 кГц, 6,70 кГц и 3,00 кГц. Ширина элемента разрешения по частоте стандартной операции ДПФ составляла 687 Гц. Спектральные функции исходного подхода при ОСШ источников 40 дБ для порядков модели 4, 20, и 40 для относительных интервалов анализа 4/64, 20/64 и 40/64 показаны на рисунках 5, 6 и 7 соответственно.
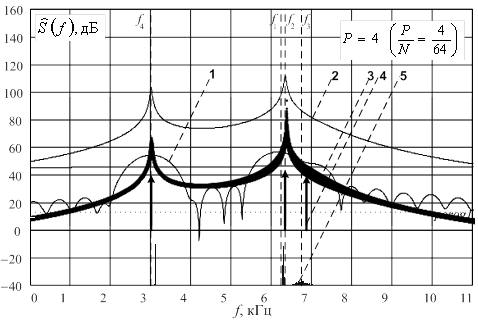
Рис.5. Спектральные функции исходного метода линейного
предсказания вперед-назад для относительного интервала анализа ![]() :
:
ДПФ выборки –1; средняя по ансамблю из 200 реализаций спектральная функция –2; ансамбль из 200 случайных реализаций спектральных функций – 3; оценки амплитуд, соответствующих корням характеристического полинома – 4, гистограммы распределения оценок частот корней характеристического полинома –5 (кривые спектральных функций приподняты по оси ординат).
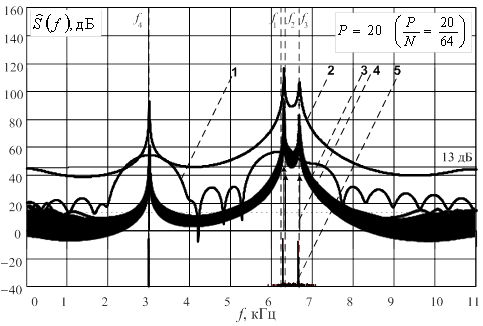
Рис.6. Спектральные функции исходного метода линейного
предсказания вперед-назад для относительного интервала анализа ![]() при ОСШ 40 дБ:
при ОСШ 40 дБ:
ДПФ выборки –1; средняя по ансамблю из 200 реализаций спектральная функция –2; ансамбль из 200 случайных реализаций спектральных функций – 3; оценки амплитуд, соответствующих корням характеристического полинома – 4, гистограммы распределения оценок частот корней характеристического полинома –5 (кривые спектральных функций приподняты по оси ординат).
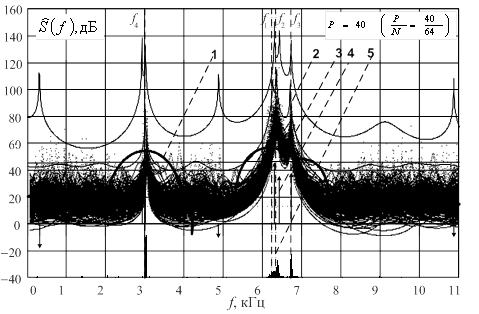
Рис.7. Спектральные функции исходного метода линейного
предсказания вперед-назад для относительного интервала анализа ![]() при ОСШ 40 дБ:
при ОСШ 40 дБ:
ДПФ выборки –1; средняя по ансамблю из 200 реализаций спектральная функция –2; ансамбль из 200 случайных реализаций спектральных функций – 3; оценки амплитуд, соответствующих корням характеристического полинома – 4, гистограммы распределения оценок частот корней характеристического полинома –5 (кривые спектральных функций приподняты по оси ординат).
Результаты обработки тестовых последовательностей фазовым и амплитудным когерентными методами (рис. 8, 9) показывают, что когерентные методы обеспечивают высокое разрешение с порядком модели 5 при относительных интервалах разрешения от 5/8 до 5/5=1, аналогичных исходному подходу. Результаты большого количества численных экспериментов подтверждают вывод о равенстве эффективности когерентного и исходного подходов при одинаковом относительном интервале анализа.
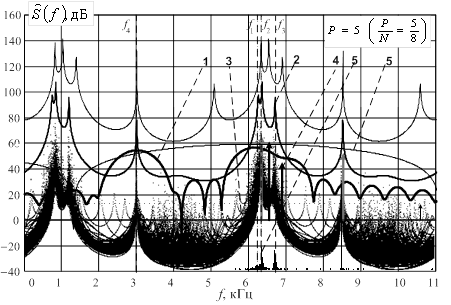
Рис.8. Спектральные функции фазового когерентного
метода линейного предсказания вперед-назад с прореживанием для относительного
интервала анализа ![]() при ОСШ 40 дБ:
при ОСШ 40 дБ:
ДПФ выборки –1; средняя по ансамблю из 200 реализаций спектральная функция –2; ансамбль из 200 случайных реализаций спектральных функций – 3; оценки амплитуд, соответствующих корням характеристического полинома – 4, гистограммы распределения оценок частот корней характеристического полинома –5; АЧХ фильтра первичной обработки – 6 (кривые спектральных функций приподняты по оси ординат).
Из рисунка 9 видно, что пики спектральной функции амплитудного метода нормирования обладают наибольшей по сравнению с предыдущими исходным и когерентным фазовым методами остротой. Если обратить внимание, то в данной оценке для амплитудного метода использовался относительный интервал анализа равный почти единице, т. е. при выполнении одного блока ДПФ было задействовано 62 отсчета из 64.
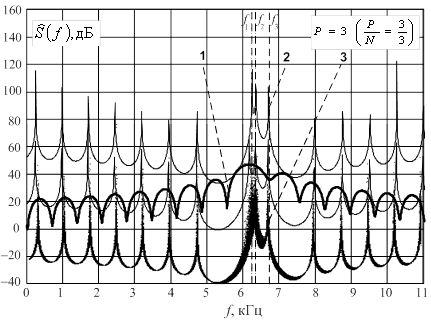
Рис.9. Спектральные функции амплитудного когерентного
метода линейного предсказания (модифицированного метода нормирования) для
относительного интервала анализа ![]() при ОСШ 40 дБ:
при ОСШ 40 дБ:
ДПФ выборки –1; средняя по ансамблю из 200 реализаций спектральная функция –2; ансамбль из 200 случайных реализаций спектральных функций – 3; (кривые спектральных функций приподняты по оси ординат).
Пример двумерной дальностно-доплеровской фазовой
когерентной спектральной оценки
Рассмотрим двумерную обработку сигнала на примере разложения пачки отраженной от групповой сосредоточенной цели сигналов с линейной частотной модуляцией (ЛЧМ) с помощью двумерного преобразования Фурье. Тестируемая модель одного такого ЛЧМ импульса была ранее рассмотрена в работе [33]. Моделировалась пачка из 32 комплексных прямоугольных ЛЧМ радиоимпульсов длительностью τ =50 мкс, периодом следования T = 10τ = 500 мкс, девиация частоты которых была равна Δfd = 2 МГц (рис. 10). Запишем дискретную модель пачки отраженных от каждого m-го источника ЛЧМ импульсов в виде
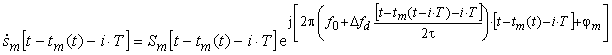
где ![]() – время задержки фронта волны,
отраженной от m-го источника;
– время задержки фронта волны,
отраженной от m-го источника;
![]() – дальность до m-го источника;
– дальность до m-го источника;
![]() ,
, ![]() –
дальность и скорость m-го источника
на момент начала зондирования;
–
дальность и скорость m-го источника
на момент начала зондирования;
![]() – скорость света;
– скорость света;
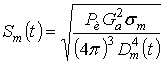 –
амплитудная функция времени;
–
амплитудная функция времени;
![]() –
пиковая мощность зондирующего сигнала;
–
пиковая мощность зондирующего сигнала;
![]() –
коэффициент направленного действия антенны в направлении главного максимума ее
диаграммы направленности;
–
коэффициент направленного действия антенны в направлении главного максимума ее
диаграммы направленности;
![]() –
эффективная поверхность рассеяния m-го
источника;
–
эффективная поверхность рассеяния m-го
источника;
![]() – начальная фаза волны, отраженной от m-го источника.
– начальная фаза волны, отраженной от m-го источника.
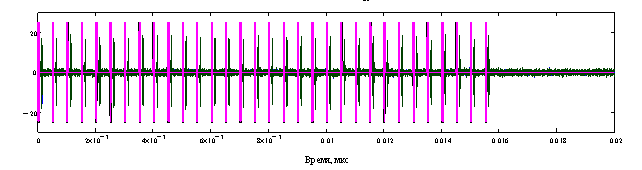
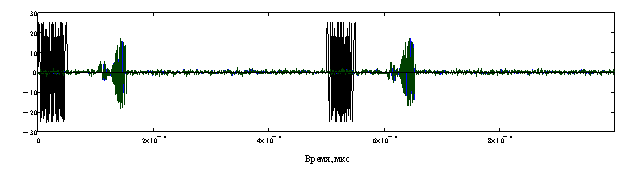
Рис. 10. Модель пачки из 32 ЛЧМ импульсов (на рисунке показаны зондирующие и отраженные от четырех целей импульсы).
Дискретная модель пачки отраженных от M источников ЛЧМ импульсов можно записать в виде
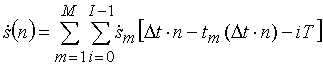 .
.
где I – количество импульсов в пачке (в нашем случае 32).
В каждом периоде зондирования осуществляется обработка отраженного ЛЧМ сигнала движущимся окном из N=128 точек [33] (рис.11).
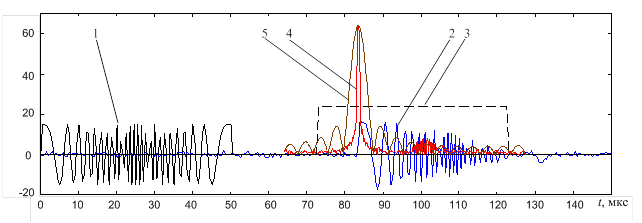
Рис. 11. Вещественные значения комплексных цифровых сигналов:
зондирующий сигнал –1; сигнал, отраженный от трех точечных целей на дальностях 12500 м, 12530 м и 12560 м, движущихся со скоростью 100 м/с в направлении локатора –2; текущее положение движущегося окна –3; модуль сжатого отраженного сигнала –4; (ОСШ для пика сжатого сигнала каждой из целей составляло 36 дБ); временная функция строба дальности, определяемого фильтром предварительной обработки с прямоугольной АЧХ – 5.
К выборке отраженного сигнала в i-м периоде зондирования, стробированной движущимся окном, применялась операция ДПФ
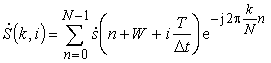 ,
,
где ![]() – номер
отсчета начала движущегося окна; k – индекс частоты (рис.11). Результат ДПФ представлен на рисунке 12
(спектр 1).
– номер
отсчета начала движущегося окна; k – индекс частоты (рис.11). Результат ДПФ представлен на рисунке 12
(спектр 1).
Умножая k-е значения ДПФ выборки ![]() (рис. 12, кривая 1) на k-е значения ДПФ (рис.12, кривая 3)
(рис. 12, кривая 1) на k-е значения ДПФ (рис.12, кривая 3)
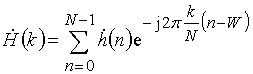
импульсной характеристики
согласованного фильтра ![]() , являющейся комплексно-сопряженной
копией зондирующего сигнала, получим спектр (рис.12, кривая 2)
, являющейся комплексно-сопряженной
копией зондирующего сигнала, получим спектр (рис.12, кривая 2) ![]() сжатого импульса в i-м периоде зондирования, обратный ДПФ
сжатого импульса в i-м периоде зондирования, обратный ДПФ
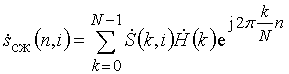
которого даст временную функцию сжатого сигнала (рис. 11, кривая 4) i-го периода зондирования. Как видно из рисунка 11 по отклику согласованного фильтра ЛЧМ сигнала цели не разрешаются, так как находятся в пределах релеевского элемента разрешения, то есть разность радиальных расстояний не превышает величины 75 м.
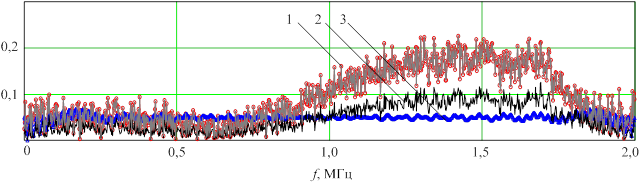
Рис. 12. Модули спектральных функций полученных с помощью ДПФ:
модуль ДПФ сигнала, отраженного от трех точечных целей на дальностях 12500 м, 12530 м и 12560 м –1; модуль сжатого отраженного сигнала –2; АЧХ согласованного фильтра– 3.
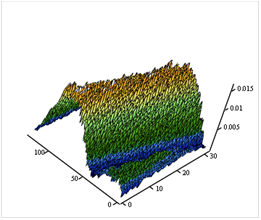
Выполняя аналогичную операцию для одноименных окон дальности в каждом из 32-х периодов зондирования, получим спектрограмму пачки из 32 ЛЧМ сигналов размером 128×32, состоящую из 32 спектров сжатых ЛЧМ импульсов (рис.13 а, б).
Выполняя ДПФ по 32 точкам в каждом n-м срезе временной
функции сжатого импульса ![]() , т. е.
, т. е.
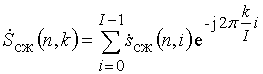 ,
,
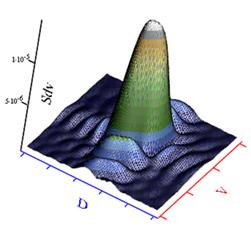
получим дальностно-доплеровский спектр (изображение) отраженной пачки ЛЧМ импульсов (рис 13 в).

а б
в г
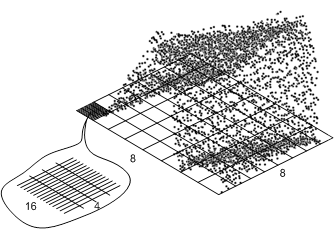
Рис. 13. Спектрограмма пачки из 32-х сжатых ЛЧМ импульсов
двумерное изображение спектрограммы –а; трехмерное изображение спектрограммы –б; двумерное дальностно- доплеровское преобразование –в; разбиение спектрограммы на субблоки данных– г .
Определив частоту
и дальность пика двумерного дальностно- доплеровского спектра, следует
сформировать прореженную выборку откликов двумерных дальностно- доплеровских
фильтров. Для этого вся спектрограмма ![]() из 128×32 отсчетов делится на 64
блока, в каждом из которых N1=16×I1=4
отсчетов (рис.13 г). В пределах каждого из блоков отсчеты когерентно суммируются
и вычисляются отсчеты прореженной двумерной выборки откликов
из 128×32 отсчетов делится на 64
блока, в каждом из которых N1=16×I1=4
отсчетов (рис.13 г). В пределах каждого из блоков отсчеты когерентно суммируются
и вычисляются отсчеты прореженной двумерной выборки откликов
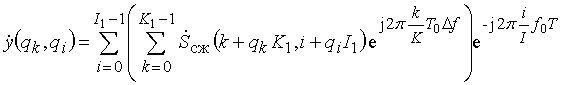
фильтров с двумерными дальностно- доплеровскими характеристиками (частотно-временными строб функциями) вида
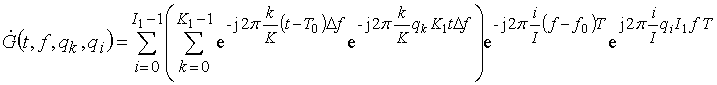 .
.
После двумерного прореживания выборки задача решается также как и в одномерном случае. Сначала составляется система уравнений двумерной модели авторегресии (рис.14), каждое из которых составляется из блока данных размерностью P (порядок модели авторегресии). На примере был рассмотрен порядок модели P = 8, объединяющие 9 блоков прореженных данных, обработанных когерентным суммированием 16×4 отсчетов притом, что прореженная двумерная выборка состоит из 8×8 отсчетов. Для моделируемого случая система уравнений линейного предсказания вперед-назад для первых яти блоков из 9 отсчетов представлена в виде
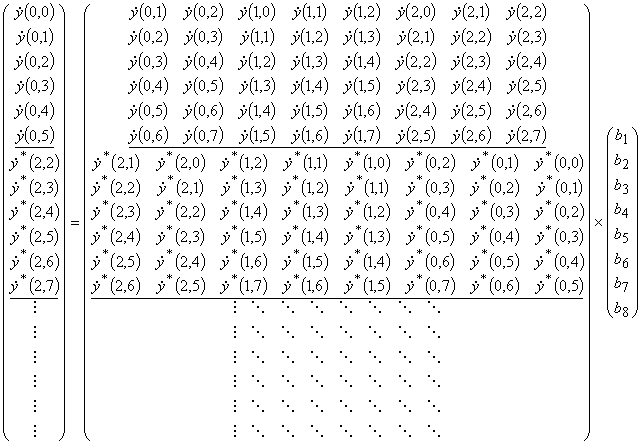 . (40)
. (40)
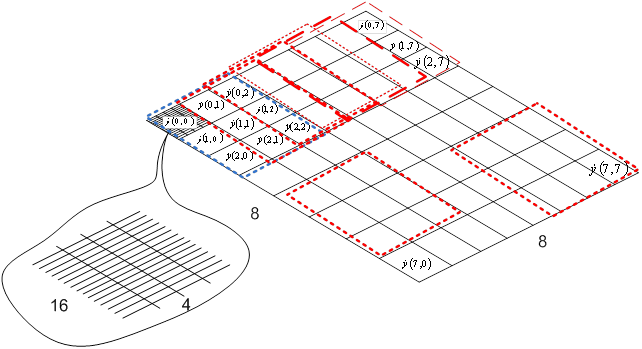
Рис. 14. Составление системы уравнений из спектрограммы пачки из 32-х сжатых ЛЧМ импульсов.
Система уравнений (40) представляет собой переопределенную систему из 6-и таких блоков уравнений представленных в (40). В настоящей работе ввиду сложности построения такой системы уравнений приведен пример, так как построение такой схемы в общем виде только усложняет выкладки и понимание сути. Решая такую систему уравнений относительно весовых коэффициентов можно получить двумерную спектральную функцию вида
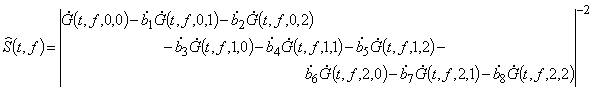 .
.
Спектральная функция, построенная для сигнальной ситуации с четырьмя целями, приведена на рисунке 15.
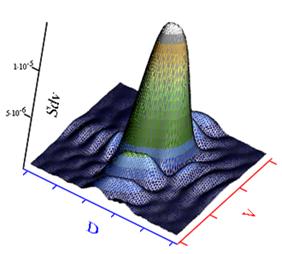
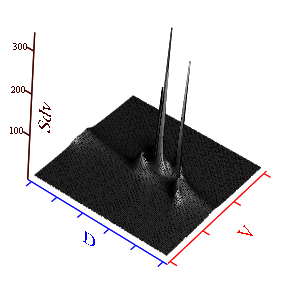
а б
Рис. 15. Спектральные функции: ДПФ –а; линейного предсказания –б;
Амплитудные и фазовые методы обработки данных в задачах пространственного анализа угловых координат источников излучения
При наличии больших вычислительных ресурсов в радиолокаторах наиболее выгодно анализировать сигнал сразу по нескольким координатам и параметрам, например, по частоте и времени, либо по пространству и частоте или по пространству и времени. В зависимости от типа радиолокатора можно применять различные многомерные комбинации при разложении сигналов.
С точки зрения пространственной обработки сигналов цели для радиолокаторов вне зависимости от типа сигнала представляют собой источники пространственных гармоник, с частотами, определяемыми углами падения волны. Поэтому все приведенные методы обработки уместны для пространственной области при наличии цифровых антенных решеток.
Перед началом процедур сверхразрешения следует определить угловые координаты, дальность и скорость группы близко расположенных источников, которые необходимо разделить. Для этого на каждом такте дискретизации по времени выполняется двумерное ДПФ по пространству (рис.16). Одноименные отсчеты сигналов по времени в каждом периоде повторения также подвергаются доплеровской обработке с помощью ДПФ, в результате чего для каждого пространственного фильтра формируется дальностно-доплеровский двумерный портрет. Такая система позволяет анализировать в каком пространственном и дальностно- доплеровском фильтре находятся источники сигналов и выбирать систему фильтров КПО в окрестности угловых координат, дальности и скорости кажущегося центра источников. После измерения положения кажущегося центра источников можно переходить к выбору системы пространственных и дальностно- доплеровских КПО для реализации процедур спектрального анализа со сверхразрешением в пределах импульсного объема, определяемого шириной диаграммы направленности пространственных фильтров, а также элементом разрешения по дальности.
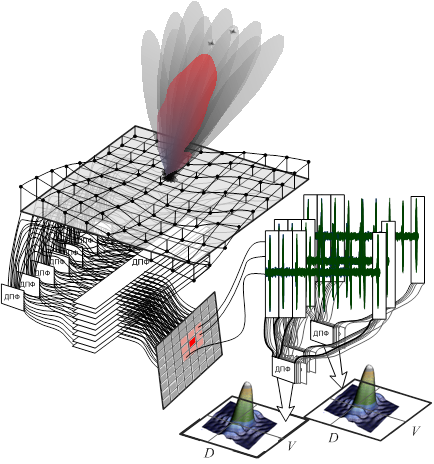
Рис.16. Схема многомерного ДПФ анализатора, использующего систему пространственных, частотных фильтров и стробов дальности типа «арочный синус» с разными амплитудными диаграммами направленности и идентичными фазовыми диаграммами направленности.
Амплитудный когерентный пространственный анализатор линейного предсказания представляет собой совокупность аппаратно-программных средств реализующих когерентный амплитудный метод линейного предсказания с когерентным накоплением по пространству. Сначала на апертуре цифровой решетки выделяются L блоков пространственных отсчетов (рис. 17), по которым выполняется пространственный ДПФ с дополнением нулями. Затем определяются Q пространственных фильтров в окрестности кажущегося центра источников, а выходные сигналы каждого q-го пространственного фильтра подвергаются дальностно-доплеровской обработке.
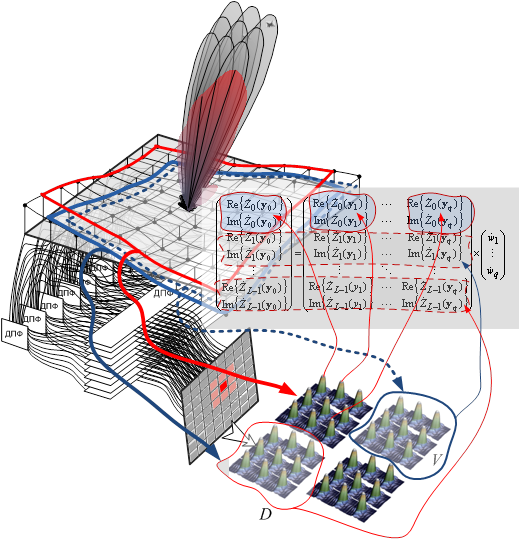
Рис. 17. Схема амплитудного когерентного пространственного анализатора линейного предсказания.
Из вещественных и
мнимых значений комплексных отсчетов пиков Q дальностно-доплеровских портретов составляются вещественное и
мнимое уравнения модифицированного метода нормирования (см. выше). В
многомерной интерпретации под y можно
подразумевать обобщенную координату, включающую в свой состав угол места,
азимут, дальность и скорость ![]() , где
, где ![]() – угловые координаты
максимума q-го пространственного фильтра. Величины
– угловые координаты
максимума q-го пространственного фильтра. Величины ![]() и
и ![]() значения
дальности и скорости, соответствующих пику дальностно-доплеровского портрета.
Для L блоков
пространственных отсчетов выполняются аналогичные операции, после чего система
уравнений решается методом наименьших квадратов и вычисляются весовые коэффициенты.
Для построения двумерной пространственной спектральной функции ХН выбранных Q пространственных фильтров складываются с
весовыми коэффициентами, вычисляется результирующая ХН, после чего вычисляются
значения обратно пропорциональные квадрату ее нормы.
значения
дальности и скорости, соответствующих пику дальностно-доплеровского портрета.
Для L блоков
пространственных отсчетов выполняются аналогичные операции, после чего система
уравнений решается методом наименьших квадратов и вычисляются весовые коэффициенты.
Для построения двумерной пространственной спектральной функции ХН выбранных Q пространственных фильтров складываются с
весовыми коэффициентами, вычисляется результирующая ХН, после чего вычисляются
значения обратно пропорциональные квадрату ее нормы.
Фазовый когерентный пространственный анализатор линейного предсказания с прореживанием представляет собой совокупность аппаратно-программных средств реализующих фазовые методы линейного предсказания с когерентным накоплением по пространству. Сначала на апертуре цифровой решетки выделяются P блоков пространственных отсчетов (рис. 18), в пределах которого отсчеты когерентно суммируются. Такой блок представляет собой пространственный фильтр с ХН, фазированной в направлении обнаруженных источников. Затем определяются Q из P пространственных фильтров в окрестности кажущегося центра источников, а выходные сигналы каждого q-го пространственного фильтра подвергаются дальностно-доплеровской обработке. С помощью Q пространственных фильтров, объединенных в блок, составляется уравнение (рис. 6). Решением системы уравнений методом наименьших можно получить ВВК, формирующий двумерную пространственную спектральную функцию.
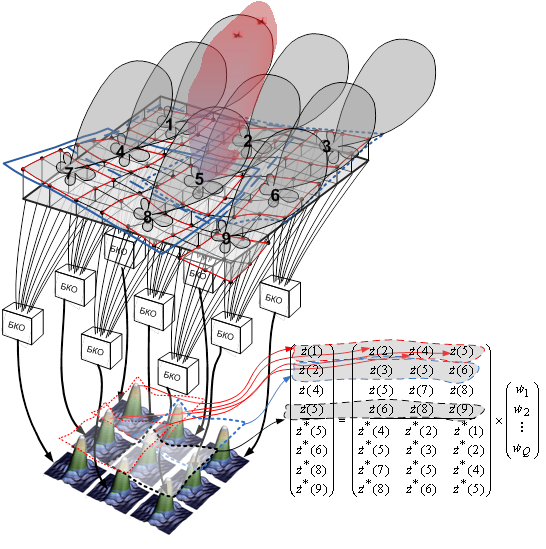
Рис. 18. Схема фазового когерентного пространственного анализатора линейного предсказания (БКО – блок когерентной обработки).
Частным случаем
такого пространственного анализатора может являться моноимпульсная цифровая
антенная решетка с пространственными каналами, показанными на рисунках 19 и 20.
Пространственная спектральная функция прореженной пространственной антенной
решетки как функция угловых координат ![]() может быть представлена в виде
может быть представлена в виде
![]() ,
,
где ![]() – комплексная
характеристика направленности q-го пространственного
канала. При наличии ограниченного количества каналов матрица данных может быть
сформирована с использованием отсчетов разных временных или частотных позиций.
– комплексная
характеристика направленности q-го пространственного
канала. При наличии ограниченного количества каналов матрица данных может быть
сформирована с использованием отсчетов разных временных или частотных позиций.

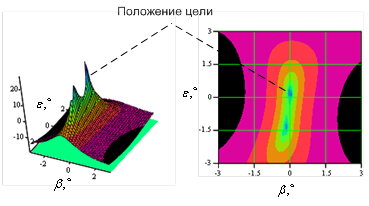
а б в
Рис. 19. Схема фазового пространственного анализатора линейного предсказания с когерентным накоплением и прореживанием по пространству четырьмя пространственными ФПО.
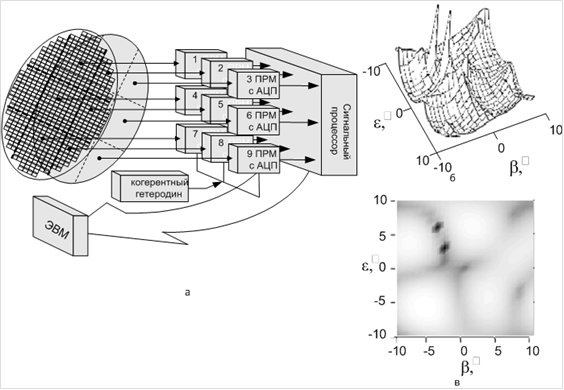
Рис. 20. Схема девятиканального фазового пространственного анализатора линейного предсказания с когерентным накоплением и прореживанием –а; двумерные пространственные функции трех источников излучения – б, в; ПРМ с АЦП – приемник с аналогово-цифровым преобразователем; ЭВМ – электронная вычислительная машина.
Заключение
Подводя итоги, следует отметить, что рассмотренные в статье когерентные подходы могут быть использованы при обработке сигналов в пространственной, во временной и частотной областях.
Аналогичное исходному подходу сверхразрешение когерентных методов достигается при существенно меньшем порядке модели не из-за когерентности накопления сигнала в элементах корреляционной матрицы, а меньшим числом обусловленности корреляционной матрицы подпространства сигналов. При этом относительные интервалы анализа, равные отношению порядка модели к общему количеству отсчетов остаются одинаковыми.
При одинаковых порядках модели вследствие лучшей обусловленности когерентные методы существенно выигрывают по сравнению с исходными подходами.
При обработке реальных сигналов из-за присутствия в смеси с шумами всевозможных составляющих, обусловленных как отражениями от пространственно распределенных пассивных помех, так и турбинными и другими эффектами следует также принимать меры предварительной фильтрации. Присутствие таких составляющих может существенно ухудшить или свести сверхразрешение полностью на нет, так как для авторегрессионных методов спектрального анализа количество гармоник, присутствующих в спектре, должно быть меньше выбранного порядка модели. Поэтому крайне необходимо перед оцениванием прибегать к операциям предварительной обработки сигналов и выделения участков спектра, интересующих в плане сверхразрешения.
Литература
1. Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения / Пер. с англ. М.: Мир, 1990.
2. Stoica P, Moses R. L. Introduction to Spectral Analysis. New Jersey, Prentice-Hall, Inc. 1997, 319 p.
3. Ширман Я. Д. Разрешение и сжатие сигналов. М.: «Сов. Радио», 1974, 360 с.
4. Варюхин В. А., Покровский В. И., Сажно В. Ф. О точности измерения угловых координат нескольких источников с помощью антенной решетки// Радиотехника и электроника. 1984. № 4.
5. Варюхин В. А. Основы теории многоканального анализа. – Киев, ВА ПВО СВ им. А. М. Василевского. 1993.
6. Курикша А. А. Оценка числа и параметров компонент сигнала при наличии шума// Радиотехника и электроника, 1984. №9. С. 1740-1744.
7. Шинаков Ю. С., Сперанский В. С. "Совместное обнаружение, разрешение и измерение параметров сигналов на фоне помех на выходе антенной решетки. Синтез алгоритмов", "Радиотехника и электроника", 1982, т. 27, № 11, с. 2179-2184.
8. Шинаков Ю. С. "Совместное обнаружение и разрешение неизвестного числа сигналов", "Радиотехника и электроника", 1985, т. 30, №6, с. 1131-1138.
9. Фалькович С. Е., Коновалов Л. Н. "Разрешение неизвестного числа сигналов"", "Радиотехника и электроника", 1982, т. 27, № 1, с. 92-97.
10. Черемисин О. П. "Адаптивные методы определения числа и пространственных параметров сигналов в многоканальных приемных системах", "Радиотехника и электроника", 1986, т. 31, № 3, с. 499-508.
11. Черемисин О. П. Эффективность адаптивных методов пеленгации помех// Радиотехника и электроника. 1989. Т. 34, № 9. С. 1850–1857.
12. Ермолаев В.Т., Родыгин Ю.Л., Флаксман А.Г. Методы определения вектора пространственной адаптивной обработки при короткой выборке помехи // Изв. Вузов. Радиофизика. 1994. Т.37, № 4. С. 493-509.
13. Дрогалин В.В. Алгоритмы оценивания угловых координат источников излучений, основанные на методах спектрального анализа. /В.В. Дрогалин и др.. // Успехи современной радиоэлектроники. 1998. №2. — 3-17
14. Леховицкий Д. И., Флексер П. М., Атаманский Д. В., Кириллов И. Г. Статистический анализ некоторых «сверхразрешающих» методов пеленгации источников шумовых излучений в антенных решетках при конечном объеме обучающей выборки//Антенны, 2000, №2, с. 23–39.
15. Слюсар В. И. Интерпретация метода Прони для решения дальномерных задач// Радиоэлектроника: Изв. Вузов. 1998. № 1. С. 61–67.
16. Царьков Н. М. Многоканальные радиолокационные измерители. М., Сов. радио, 1980.
17. Ратынский М. В. Адаптация и сверхразрешение а антенных решетках – М.: Радио и связь, 2003. – 200 с.
18. Абраменков В. В. Накопление сигнала при использовании современных методов спектрального анализа// Радиотехника. 2002. № 12. С. 88–91.
19. Абраменков В. В., Жибуртович Н. Ю., Климов С. А., Савинов Ю. И., Чижов А. А. Оценка влияния искажений характеристик направленности элементов антенных решеток на эффективность измерения угловых координат методом Прони// Информационно-измерительные и управляющие системы, 2005. Т.3. №6. С. 36-41.
20. Савинов Ю. И. Когерентный метод Прони с квазипрореживанием// Вопросы радиоэлектроники. Серия РЛТ. Вып. 3, 2008 - С. 122-128.
21. Абраменков В. В. Измерение угловых координат М источников излучения методом нормирования сигнала к амплитудам образовавших его источников//Сб. статей. Авионика 2002 – 2004. М.: Радиотехника, 2005. С. 218 – 221.
22. Савинов Ю. И. Метод Прони. Смоленск: ВА ВПВО ВС РФ им. А. М. Василевского, 2008, 87 с.
23. Нечаев Ю.Б. Метод оценки количества сигналов в задачах радиопеленгации при небольшом времени наблюдения / А. Зотов, Ю.Б. Нечаев // Изв. вузов. Радиоэлектроника. — 2008. — № 6 — 3-9.
24. Аджемов С. Исследование алгоритмов сверхразрешения в адаптивных антенных решетках. / С. Аджемов, Г.О. Бокк, А.Г. Зайцев и др.. // Радиотехника. — 2000. —№11. — 66-71.
25. Сычев М.И. Пространственно-временная обработка радиосигналов на основе параметрического спектрального анализа // Антенны. — 2001. — вып. 1(47). — С . 70-77.
26. Добырн В.В. Эффективность применения сверхразрешающих спектральных оценок в бортовых угломерных фазированных антенных решетках /В.В. Добырн, А.В. Немов // Радиотехника. — 1999. — №9. 65-67.
27. Ганков И.В. Предельные характеристики сверхразрешения когерентных источников при предварительной декорреляции выборки. Радиотехника, 1994. — №10. — 23-27
28. Григорян Д. С. Определение области сверхразрешения источников излучения по пространству при собственных шумах и неидентичностях приемных трактов// Радиотехника. 2007. № 8. С. 43–48.
29. Григорян Д. С. Влияние неидентичностей амплитудно-частотных характеристик приемных каналов цифровой антенной решетки на возможность сверхразрешения источников излучения по пространству// Радиотехника. 2009. № 10. С. 27–36.
30. Беклемишев Д. В. Дополнительные главы линейной алгебры. М.: Наука. Главная редакция физико-математической литературы, 1983. – 336 с.
31. Финкельштейн М. И. Основы радиолокации: Учебник для вузов. – 2-е изд. перераб. и доп. – M.: Радио и связь, 1983. – 536 с.
32. Григорян Д. С. Сверхразрешение по частоте при обработке радиолокационных сигналов когерентными методами линейного предсказания вперед-назад с прореживанием данных– "Журнал радиоэлектроники": электронный журнал. - 2011. - №7. URL: http://jre.cplire.ru/jre/jul11/7/text.html
33. Григорян Д. С. Сверхразрешение по дальности при обработке радиолокационных сигналов с линейной частотной модуляцией когерентным методом линейного предсказания вперед-назад с прореживанием данных – "Журнал радиоэлектроники": электронный журнал. - 2011. - №8. URL: http://jre.cplire.ru/jre/aug11/2/text.html