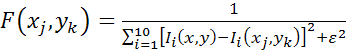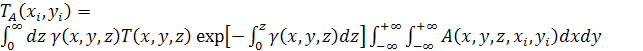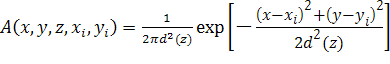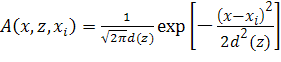Определение положения и размера нагретой области методом динамической акустотермографии
А. А. Аносов 1,2, А. С. Казанский 1, А. Д. Мансфельд 3 , А. С. Шаракшанэ 1
1 Институт Радиотехники и Электроники РАН им. В. А. Котельникова
2Первый Московский Государственный Медицинский Университет им. И. М. Сеченова
3 Институт прикладной физики РАН
Получена 25 марта 2013 г.
Аннотация. Рассмотрен вопрос определения размера и расположения нагретой области, которая возникает в результате медицинских процедур: гипертермии или термоабляции. Параметры области меняются во времени: для их измерения предлагается использовать динамическую акустотермографию. Проведены компьютерное моделирование и физические эксперименты, в которых решили одномерную и трехмерную пространственные задачи. В 3D эксперименте использовали две плоских решетки из 7 акустических датчиков каждая, расположенные перпендикулярно друг другу. Показано, что для определения координат центра и размера нагретой области с погрешностью около 1-3 мм достаточно времени усреднения 10 с. Полученные результаты важны для контроля температуры при проведении медицинских процедур, связанных с нагревом внутренних тканей организма человека. Материалы статьи докладывались на VI Всероссийской конференции "Радиолокация и радиосвязь".
Ключевые слова: тепловое акустическое излучение, динамическая акустотермография, восстановление температуры.
Abstract. Size and location detection of heated region which appears in result of medical procedures such as hyperthermia and thermoablation is discussed. The region parameters are changed over time. The dynamical acoustical thermography is proposed for their measurements. Computer simulation and natural experiments are carried out. In these experiments the 1D and 3D reconstruction problems are solved. In the 3D experiment two plane arrays are used. Each array consists of 7 acoustical sensors. The arrays are perpendicular each other. It is shown that the average time 10 s is enough to detect the size and location of heated region with error about 1-3 mm. The obtained results are important for the temperature control of the medical procedures connected with heat of the soft tissues of the human body. The results of the paper were presented at Conference "Radars and Communications 6".
Keywords: thermal acoustic radiation, dynamical acoustical thermography, temperature reconstruction.
Введение.
При медицинских процедурах, связанных с нагревом внутренних тканей организма человека (например, при гипертермии или термоабляции), необходим контроль меняющегося во времени и в пространстве температурного распределения [1]. Это важно, потому что перегрев может привести к поражению здоровой ткани, а недостаточный нагрев не даст терапевтического эффекта. Отметим, что кроме определения температуры существенным вопросом является определение размеров и расположения нагретой области. Врачей интересует вопросы, связанные с распространением тепла и размером нагретой области. Оптимальными для измерения глубинной температуры являются безболезненные неинвазивные методы. В ряде случаев для этого можно использовать акустотермографию, при которой измеряют тепловое акустическое излучение объекта [2-12].
Мы провели компьютерное моделирование с целью определения размеров и расположения нагретой области, положение которой меняется в пространстве. Проведены натурные эксперименты с модельными объектами, в которых определяли положение нагретой области в пространстве, ее размер и эффективную температуру.
Экспериментальные схемы.
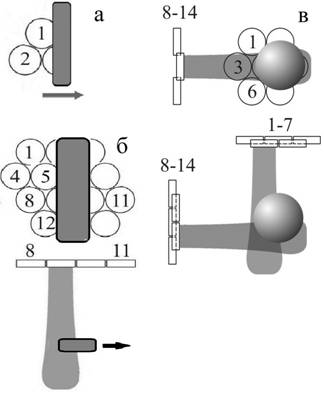
Для акустических измерений были использованы два многоканальных акустотермографа [13-17], разработанные в ИПФ РАН группой под руководством А. Д. Мансфельда: 6-канальный (полоса приема 1.7±0.4 МГц, диаметр приемника – 10 мм) и 16-канальный (полоса пропускания 1.2-2.7 МГц, диаметр датчика 8 мм). Пороговая чувствительность акустотермографов при времени интегрирования 10 с составляла 0.2 К. Модельные эксперименты проводили в аквариуме размером 40 ´ 60 ´ 20 см3, заполненном водой. Температуру воды в аквариуме контролировали электронными термометрами с точностью до 0.3 К. Были использованы три схемы измерений, три варианта приемных решеток: решетка из трех датчиков, расположенных пирамидой (показана на рис. 1а), плоская двумерная решетка, состоящая из 14-и датчиков (см. рис. 1б), две плоские решетки, перпендикулярные друг другу, каждая состоит из 7-и датчиков (рис. 1в). Принимаемые датчиками акустические сигналы преобразовывались в электрические. Электрические сигналы усиливались, проходили через квадратичный детектор и усреднялись в течение 30 мс. С выхода акустотермографа сигналы подавались на 14-ти разрядный многоканальный АЦП Е14-140 (ЗАО «L-Card») с частотой дискретизации 1 кГц на один канал и поступали в компьютер. Разработанная программа проводила дальнейшее усреднение данных. В качестве источников теплового акустического излучения использовали нагреваемые пластилиновые тела различной формы: длинную полосу (см. рис. 1а, б) и шар (рис. 1в). Внутри пластилина находились электрические сопротивления 40 – 100 Ом. При подаче постоянного напряжения 12 – 25 В пластилин за 30 с нагревался на 10 – 20 К относительно воды в аквариуме. Внутреннюю температуру пластилиновых тел контролировали электронными термометрами с точностью до 0.3 К.
Рис.
1.
Схемы экспериментов: а) решетка из 3-х датчиков (фронтальная проекция, расстояние
между центрами соседних датчиков 20 мм);
б) решетка из 14-и датчиков
(фронтальная проекция и вид сверху, расстояние между центрами соседних датчиков
10 мм);
в) две решетки из 7 датчиков каждая (фронтальная проекция и вид сверху,
расстояние между центрами соседних датчиков 10 мм).
Стрелками показано
направление движения вытянутой нагретой пластилиновой полосы,
цифрами - номера
датчиков, серым цветом - их диаграммы направленности.
Компьютерная модель 1.
В статье рассмотрены две математические модели, позволяющие определять параметры пространственного температурного распределения. Задача первой модели заключалась в восстановлении положения перемещающегося в пространстве теплового источника. Рассматривался двумерный случай. Тепловой источник задали в виде прямоугольника размером 1 ´ 4 см2, который мог перемещаться в поле размером 20 ´ 35 см2 (см. рис. 2). Сигнал от источника приходил на решетку из 10 датчиков (АТ1-10), расположенных с одной стороны исследуемой области.
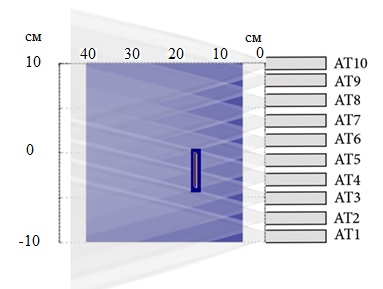
Рис. 2. Геометрическая схема для компьютерной модели 1.
Поле перемещения
теплового источника и 10 датчиков (АТ1-10).
В представленной конфигурации центр
источника имеет координаты: x = -2 см, y = 15 см.
За основу были взяты 400 (матрица 20 ´ 20) положений теплового источника в исследуемой области. Для каждого положения предварительно были рассчитаны сигналы, "измеряемые" всеми 10-ю датчиками: Ii (xj, yk), i = 1...10, j = 1...20, k = 1...20. Эти 4000 значений составляли базу данных, которая использовалась для определения положения источника.
Источник перемещался по исследуемой области. При каждом положении источника рассчитывались сигналы, измеряемые всеми 10-ю датчиками: Ii (x, y), i = 1...10. После этого строился двумерный образ F(xj, yk) источника:
Если положение (x, y) совпадало с (xj, yk), то образ источника был максимальным и равным 1/e2, где e заранее выбранное небольшое число. Предлагаемая модель дала представление о степени неопределенности решения обратной задачи восстановления пространственных параметров температурного распределения.
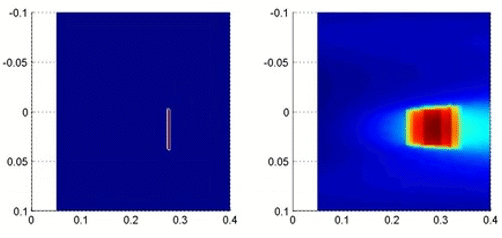
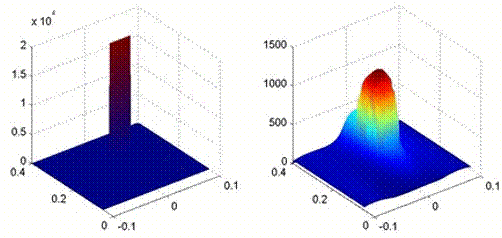
На рис. 3 приведены результаты компьютерного моделирования. На левых диаграммах показано, как нагретый прямоугольный источник размером 1 ´ 4 см2 перемещался по плоскости в двух направлениях. На правых диаграммах показано перемещение его восстановленного образа. Из сравнения диаграмм видно, что положение и размер нагретого объекта в направлении вдоль линии расположения датчиков (в латеральном направлении) восстанавливались с приемлемой точностью. В то же время, положение и размер источника в направлении вглубь исследуемой области (в трансверсальном направлении) восстанавливались с большой погрешностью.
Рис. 3а. Для просмотра анимации кликните на изображение или на ссылку
Рис. 3б. Для просмотра анимации кликните на изображение или на ссылку
Рис.
3.
Перемещение нагретого источника (слева) и его восстановленного образа (справа):
а) карта перемещения (по осям - координаты в метрах),
б) объемное изображение
(по вертикальной оси - акустояркостная температура в относительных единицах,
по
горизонтальным осям - координаты в метрах).
Предлагаемая модель дала возможность наглядно увидеть степень неопределенности восстановления положения и размера нагретой мишени в трансверсальном направлении. Для решения этой задачи необходимо использование нескольких решеток датчиков, расположенных под углом друг к другу. Для анализа особенностей восстановления положения, размера и температуры нагретого объекта была предложена вторая модель.
Компьютерная модель 2.
Вторая модель позволяла определять положение, характерные размер и температуру нагретой области. При этом предполагалось, что распределение глубинной температуры T исследуемого объекта является функцией Гаусса. В одномерном случае:
где x0 определяет положение (координату центра), Tmax и D – характерные температуру и размер нагретой области. В трехмерном случае:
где добавляются еще две пространственные координаты положения нагретой области.
С учетом диаграммы направленности датчика, центр которого находится в точке (xi, yi, 0), акустояркостную температуру TA можно рассчитать по формуле [18]:
где g (x, y, z) – распределение в пространстве коэффициента поглощения (по интенсивности) ультразвука, A (x, y, z, xi, yi) - диаграмма направленности датчика, ось z совпадает с акустической осью приемника. Ноль температуры соответствует температуре воды в аквариуме. Используемые в эксперименте приемники являлись широкополосными. Поэтому в качестве диаграммы направленности датчика мы использовали (так же, как и для температуры) функцию Гаусса:
где d(z) – характерный поперечный размер диаграммы направленности датчика на расстоянии z. Если температура не меняется вдоль координаты y, то выражение для диаграммы направленности можно было упростить:
В этом случае центр датчика определялся
только одной координатой xi. Диаграммы направленности были
нормированы таким образом, чтобы интегралы от выражений (5) и (6), взятые по
поперечным координатам, не зависели от величины z: ![]() или
или ![]() , для любых
, для любых ![]() .
.
Рассмотрим случай, когда нагретая плоская пластилиновая пластина расположена напротив приемного датчика. Ось z направлена по акустической оси датчика перпендикулярно пластине. Будем считать, что в пластилине температура не меняется по оси z (по глубине). Между датчиком и пластилином находится вода, поглощением ультразвука в которой (по сравнению с поглощением в пластилине) можно пренебречь. Из-за сильного поглощения акустических волн в пластилине, основной сигнал идет из достаточно тонкого слоя, находящегося на расстоянии z от датчика. Это позволяет считать характерный размер d диаграммы направленности постоянным. Тогда, если температурное распределение подчиняется выражению (2), то есть температура не меняется вдоль координаты y, то интегрирование выражения (4), с учетом выражений (2) и (6), дает результат:
Если же температурное распределение подчиняется выражению (3), то есть распределение температуры является трехмерным, то интегрирование выражения (4), с учетом выражений (3) и (5), дает результат:
Выражения (7) и (8) допускают простую интерпретацию: учет диаграммы направленности расширяет и снижает образ температурного распределения (акустояркостную температуру) по сравнению с самим температурным распределением. Если характерный размер диаграммы направленности много меньше характерного размера нагретой области d << D, то высота и ширина зависимости акустояркостной температуры от координат центра датчика совпадают с высотой и шириной температурного распределения. Можно сказать, что ширина образа температурного распределения определяется геометрической суммой характерных размеров нагретой области и диаграммы направленности.
Вторая компьютерная модель была представлена, чтобы восстанавливать параметры: положение, характерный размер и максимальную температуру нагретой области по экспериментальным данным. Для этого минимизировали функцию F (Tmax, D, x0, y0) для 2D случая или функцию F (Tmax, D, x0) для 1D случая с целью определения температуры, положения и размера источника:
где TA (i)exp –
экспериментальные значения акустояркостных температур, TA (i) – величины, определяемые выражениями (7) или (8); суммирование проводится
по всем датчикам.
Экспериментальные результаты и их обсуждение.
Эксперимент 1. На рис. 4 показано перемещение протяженной нагретой пластилиновой полосы, фиксируемое решеткой, состоящей из 14-и датчиков (схема эксперимента, представленная на рис. 1б). Поперечный размер пластины 1 см совпадал с расстоянием между центрами приемных датчиков. Это приводило к искажениям изображения и к необходимости дальнейшей обработки экспериментальных данных согласно модели 2.
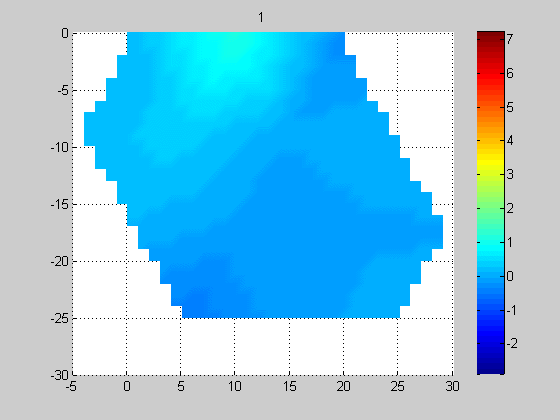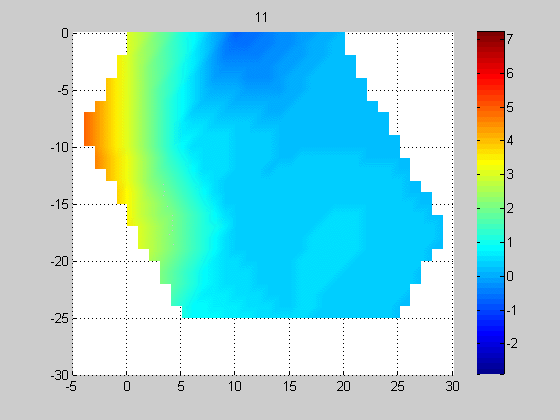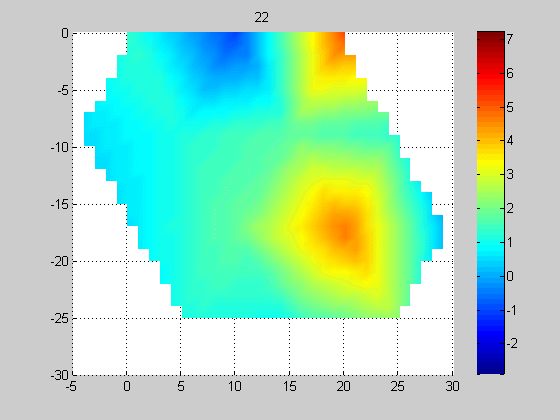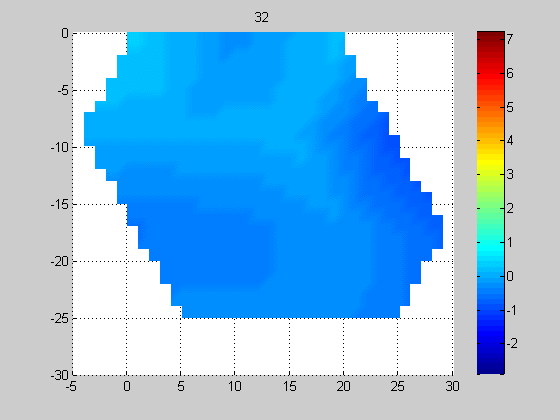
Рис. 4. Перемещение (с шагом 5 мм) нагретой вертикальной пластины шириной 10 мм слева направо, измеренное решеткой из 14-и датчиков. По горизонтальной и вертикальной осям значения даны в миллиметрах, цветовая шкала (справа) для акустояркостной температуры дана в Кельвинах. 0 К соответствует температуре аквариума.
Эксперимент 2. В эксперименте, показанном на рис. 5а, мишень нагревалась и передвигалась вдоль трех датчиков, установленных пирамидой (рис. 1а). Расстояние между центрами датчиков составляло 2 см. Расстояние между датчиками и прямой, вдоль которой движется мишень, составляло 5 см. Длительность эксперимента была 600 с, из них мишень находилась одновременно в поле зрения всех трех датчиков только с 350-й по 420-ю секунды. В течение этих 70-и секунд мы восстановили 14 позиций нагретой мишени, т.е. время измерения составило 5 с. В каждый момент времени путем минимизации функции (9) были восстановлены все три эффективных параметра мишени: максимальная температура Tmax, размер D и координата центра мишени x0. В этом считали, что ширина диаграммы направленности d много меньше размера мишени D: d << D. Восстановленные температурные гауссианы показаны на рис. 5б. За время эксперимента температура нагретой мишени не менялась. Восстановленный инкремент эффективной максимальной температуры составлял 35 ± 2 отн. ед. Пластина была нагрета относительно аквариума на 15 К, таким образом случайная ошибка восстановлении температуры составила около 0.8 К. Отметим, что в этом эксперименте мы не ставили себе задачу восстановить максимальную температуру нагретой пластины, поэтому ошибка восстановления показывает стабильность получаемых результатов. Ширина мишени также оставалась постоянной: восстановленное значение составило 19 ± 3 мм. Эта величина соответствовала реальной ширине нагретого объекта. Координата мишени изменялась при движении мишени, ошибка восстановления составляла не более 3 мм. Эти значения получены при времени интегрирования 5 с.
Предлагаемая модель показала, что для восстановления положения центра и размера нагретой области с погрешностью 3 мм в одномерном случае достаточно было времени усреднения 5 с. Стабильность определения эффективной температуры за то же время интегрирования составила 0.8 К. Определение параметров источника в двумерном и трехмерном случае можно осуществить масштабированием схемы трех датчиков, установленных пирамидой. Этот подход был осуществлен в третьем эксперименте.
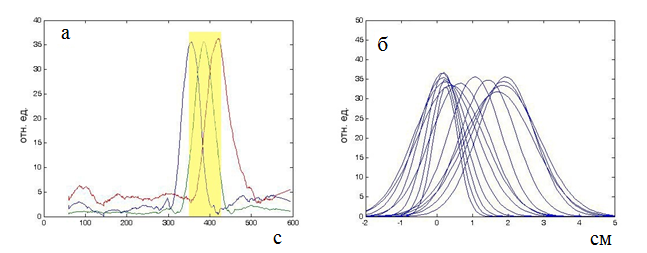
Рис.
5.
Экспериментальные кривые (а) и восстановленные температурные распределения (б),
полученные при перемещении нагретой мишени относительно трех датчиков,
установленных пирамидой:
а) временные зависимости измеренных тремя датчиками
сигналов, желтый прямоугольник показывает время,
когда экспериментальные данные
были использованы для восстановления;
б) восстановленные температурные гаусианы
(в моменты времени от 352.5 до 417.5 с через каждые 5с).
Координаты центров
датчиков: 0, 1, 2 см.
Эксперимент 3. В эксперименте, показанном на рис. 6, неподвижный пластилиновый шар нагревался и через некоторое время охлаждался. Были использованы две плоские решетки, перпендикулярные друг другу, каждая решетка состояла из 7-и датчиков (рис. 1в). Эксперимент длился 300 с, прогрев начинался на 50-й секунде и отключался на 100-й секунде. На рис. 6 представлены 30 кадров, каждый кадр был получен усреднением за 10 с. На каждом кадре представлены две карты акустояркостной температуры, полученные в двух перпендикулярных плоскостях.
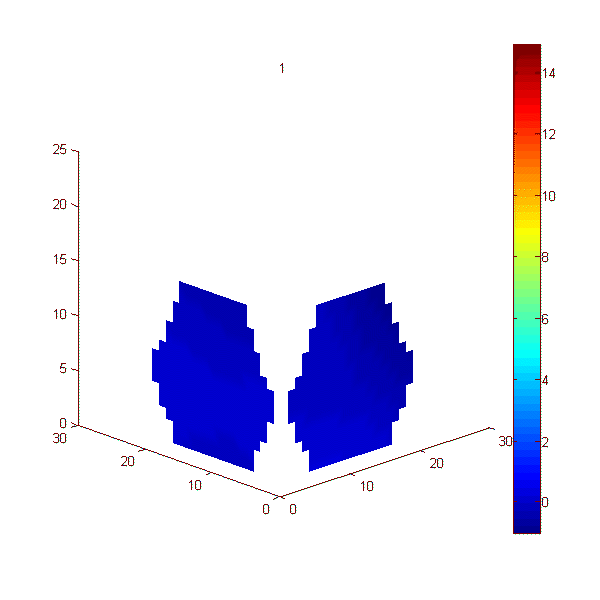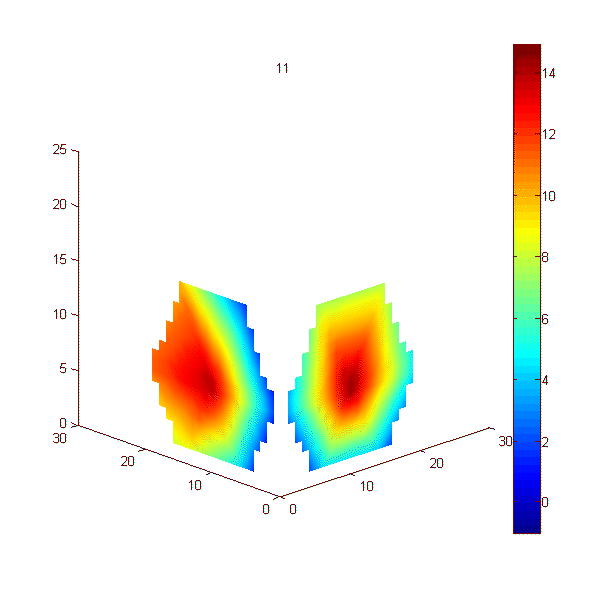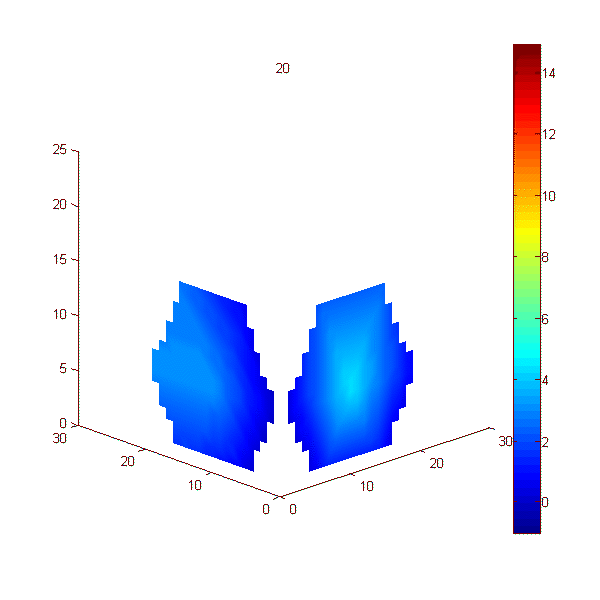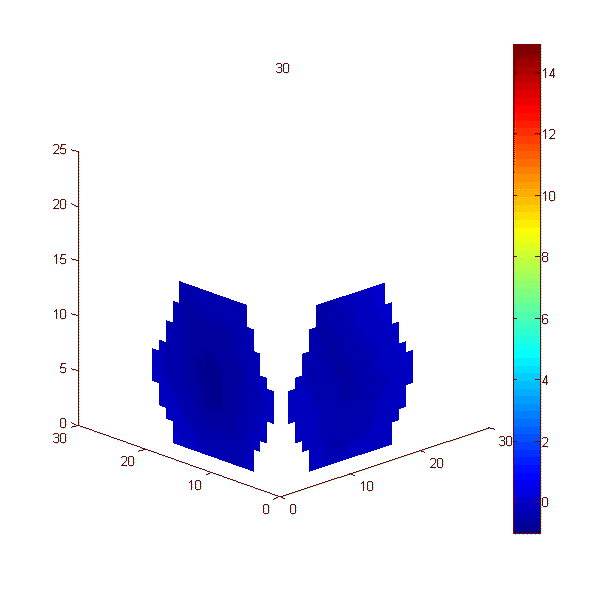
Рис. 6. Кадры с
экспериментальными картами акустояркостной температуры,
полученными в двух перпендикулярных плоскостях при нагреве пластилинового шара.
Усреднение 10 с. По осям представлены координаты центров акустических датчиков
(в миллиметрах).
Цветовая шкала (справа) показывает акустояркостную температуру
в Кельвинах.
Распределение температуры шара предполагалось в виде трехмерного гауссиана (3). Измеряемая датчиками акустояркостная температура определялась выражением (8). При этом задача объемного восстановления свелась к двум задачам 2D восстановления. Мы использовали данные одной решетки, считали пластилиновый шар плоской пластиной, расположенной на таком же расстоянии от решетки, как и центр шара, и определяли согласно выражению (8) параметры температурного распределения. Потом мы использовали данные второй решетки, опять считали пластилиновый шар плоской пластиной, но расположенной уже перпендикулярно первой, и опять согласно выражению (8) определяли параметры температурного распределения. Таким образом, одну координату (из трех) центра, размер и температуру шара мы определяли дважды, по результатам независимых измерений, проведенных с помощью двух решеток.
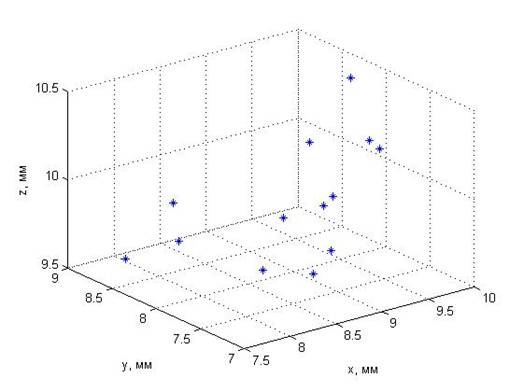
Рис. 7. Восстановленные координаты центра нагретого шара (восстановление проводилось с 65-й по 185-ю с).
Центр шара находился на расстоянии z = 4.5 см от решеток. Ширина диаграммы направленности датчика диаметром b = 8 мм, вычисленная для монохроматического сигнала частотой f = 1.95 МГц (средняя частота приема) в приближении Фраунгофера, составила d » c z / f b = 4.3 мм. В каждый момент времени путем минимизации функции (9) были восстановлены 5 параметров температурного распределения: максимальная температура Tmax, размер D и координаты центра шара x0, y0, z0. На рис. 7 представлено положение в пространстве восстановленных координат центра нагретого шара. Восстановление было начато на 65-й секунде (через 15 с после начала нагрева) и закончено на 185-й секунде, когда шар практически охладился. Из рис. 7 видно, что все восстановленные значения координат x0 = 9 ± 1 мм, y0 = 8 ± 1 мм, z0 = 10 ± 1 мм лежат внутри прямоугольника объемом 2.5 ´ 2 ´ 1 мм3. Это показывает, что погрешность восстановления положения нагретой области в пространстве (около 1 мм) меньше поперечного размера диаграммы направленности одного датчика. Это связано с тем, что в определении координаты "участвовали" все семь датчиков решетки.
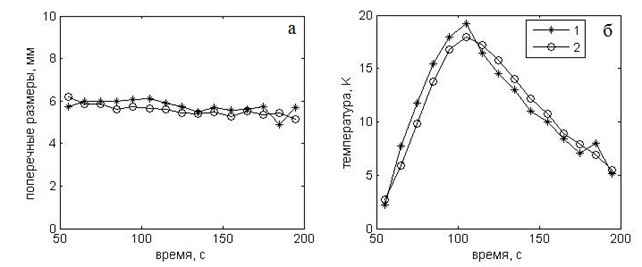
Рис. 8. Восстановленные с помощью двух решеток (1 и 2) размер и температура нагретого шара.
На рис. 8 представлены восстановленные размер и максимальная температура нагретой области. Как видно из рис. 8а, характерные размеры гауссиана, полученные с помощью первой и второй антенной решетки, практически совпали: 5.8±0.3 и 5.6±0.3 мм, соответственно. Таким образом, размер нагретой области, при котором максимальная температура уменьшается вдвое, составил 14±1 мм. Этот результат соответствует диаметру нагретого пластилинового шара 19 мм. Как видно из рис. 8б полученные по результатам измерений первой и второй антенной решеткой максимальные температуры различаются не сильно: среднее различие составляет 1.0±0.5 К. Отметим, что объемное распределение температуры внутри пластилина мы не контролировали. Найденная максимальная температура ниже реальной температуры в центре нагретого шара и выше измеренных акустояркостных температур.
Полученные данные показывают, что за время интегрирования 10 с пространственные параметры температурного распределения, например, положение и размер нагретой области можно измерить с точностью 1-3 мм. Этот результат важен для контроля температуры при проведении медицинских процедур, связанных с нагревом внутренних тканей организма человека.
Работа поддержана РФФИ (грант 13-02-00239) и Правительством РФ (грант № 11.G34.31.0066).
Литература
1. Аносов А.А., Сергеева Т.В., Алехин А.И., Беляев Р.В., Вилков В.А., Иванникова О.Н., Казанский А.С, Кузнецова О.С., Лесс Ю.А., Мансфельд А.Д., Санин А.Г., Шаракшанэ А.С., Луковкин А.В. "Акустотермометрическое сопровождение лазериндуцированной интерстициальной гипертермии молочной и щитовидной желез", Биомедицинская радиоэлектроника, 2008, №5, С.67-72.
2. Гуляев Ю.В., Годик Э.Э., Дементиенко В.В., Пасечник В.И., Рубцов А.А. "О возможностях акустотермографии биологических объектов", Докл. АН СССР. 1985. Т.283. №6. С.1495-1499.
3. Аносов А.А., В.И.Пасечник, К.М.Бограчев "Пассивная термоакустическая томография кисти руки человека", Акуст. журн. 1998. Т.44. №6. C.725-730.
4. Гуляев Ю. В., К.М. Бограчев, И. П. Боровиков, Ю. В. Обухов, В. И. Пасечник "Пассивная термоакустическая томография - методы и подходы", Радиотехника и электроника, 1998 Т.43 №9 С.140-146
5. Аносов А.А., Пасечник В.И., Исрефилов М.Г. "Восстановление двумерного распределения внутренней температуры модельного объекта методом пассивной термоакустической томографии", Акуст. журн. 1999. Т. 45. № 1. C.20–24.
6. Krotov E.V., Zhadobov M.V., Reyman A.M., "Detection of thermal acoustic radiation from laser-heated deep tissue", Appl. Phys. Lett., 2002, Vol. 81, #21, P.3918-3920.
7. Weaver R.L., Lobkis O.I. "Elastic wave thermal fluctuations, ultrasonic waveforms by correlation of thermal phonons", J. Acoust. Soc. Am. 2003. V. 113 P. 2611–2621.
8. Bosnyakov M.S., Obukhov Yu.V. "Optimum wavelet basis for representation of the functions satisfying the head conduction equation", Pattern Recognition and Image Analysis. 2003. V. 13, № 1. P. 621–624.
9. Буров В.А., Дариалашвили П.И., Евтухов С.Н., Румянцева О.Д. "Экспериментальное моделирование процессов активно-пассивной термоакустической томографии", Акуст. журн. 2004 Т.50 №3 С.298-310.
10. Миргородский В.И., Герасимов В.В., Пешин С.В. "Экспериментальные исследования особенностей пассивной корреляционной томографии источников некогерентного акустического излучения мегагерцового диапазона", Акуст. журн. 2006 Т.52 №5 С.606-612.
11. Аносов А.А., Барабаненков Ю.Н., Бограчев К.М., Гарсков Р.В., Казанский А.С., Шаракшанэ А.С. "Совместное использование акустотермографии и ИК-тепловидения для контроля температуры при нагреве модельного биологического объекта", Акуст. журн. 2008. Т.54. №3. С.499-504.
12. Godin O.A. "Retrieval of Green’s functions of elastic waves from thermal fluctuations of fluid-solid systems", J. Acoust. Soc. Am. 2009. V. 125 P. 1960–1970.
13. Мансфельд А.Д. "Акустотермометрия. Состояние и перспективы", Акуст. журн. Т.55. 2009. №4-5. С.536-547.
14. Аносов А.Н., Беляев Р.В., Вилков В.А., Казанский А.С., Мансфельд А.Д., Шаракшанэ А.С. "Определение динамики изменения температуры в модельном объекте методом акустотермографии", Акуст. журн. 2008. Т.54. №4. С.540-545
15. Аносов А.А., Беляев Р.В., Вилков В.А., Казанский А.С., Мансфельд А.Д., Шаракшанэ А.С. "Динамическая акустотермография", Акуст. журн. 2009. Т. 55. № 4–5. С.436–444.
16. Аносов А.А., Беляев Р.В., Вилков В.А., Дворникова М.В., Дворникова В.В., Казанский А.С., Курятникова Н.А., Мансфельд А.Д. "Акустотермометрическое восстановление профиля глубинной температуры с использованием уравнения теплопроводности", Акуст. журн. 2012. Т. 58. № 5. C. 592–599.
17. Аносов А.А., Беляев Р.В., Вилков В.А., Дворникова М.В., Дворникова В.В., Казанский А.С., Курятникова Н.А., Мансфельд А.Д. "Акустотермометрический контроль кисти человека при гипертермии и гипотермии", Акуст. журн. 2013. Т. 59. № 1. C.109–114.
18. Passechnik V.I. "Verification of the Physical basis of acoustothermography", Ultrasonics, 1994, V.32, P.293-299.